User:Rp1414

Transition States

Introduction

Transition states are the highest potential energy point along a reaction profile. Transition states cannot be isolated and are the point of maximum instability as bonds are being partially formed or broken. To reach the transition state the activation energy barrier must be overcome. Transition states can be depicted in potential energy surfaces (PES) which is the mathematical function of the energy of a molecule with respect to its geometry. The first order saddle points on PES correspond to transition states as they are a minimum in the surface in all directions except one. In this lab, the transition states of a variety of pericyclic reactions are located and characterised. Using computational methods to do this is highly useful as transition states are difficult to study experimentally as they exist transiently. In addition, it gives insight into the geometry of the transition state structure which can aid in calculating reaction energy profiles.

Nf710 (talk) 00:21, 20 January 2017 (UTC) This description is too vague you haven't talk about second deriviatives etc

Exercise 1: Reaction of Butadiene with Ethylene

Discussion of Molecular Orbital Diagrams

Figure 1: Reaction scheme for Butadiene and Ethylene

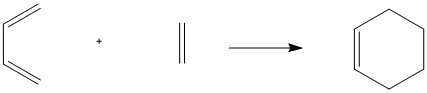
The Diels-Alder reaction between Ethylene and Butadiene is an example of a 4s+2s Woodward Hoffman reaction. The reaction was investigated using the PM6 method on Gaussian. Below in figure 2, shows the combination of molecular orbitals during the reaction. In the the reaction, the HOMO of ethene and the LUMO of butadiene combine as they are close in energy and of the same symmetry.

Figure 2: MO diagram for Butadiene and Ethylene

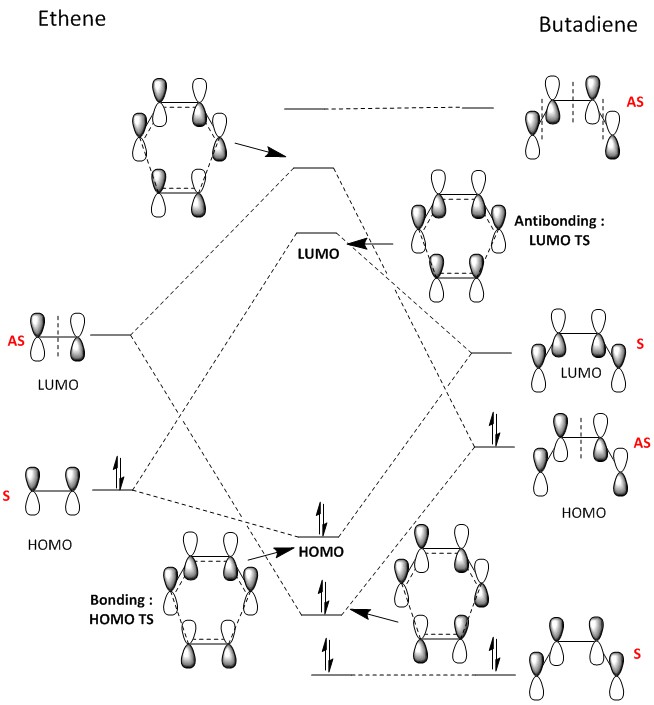
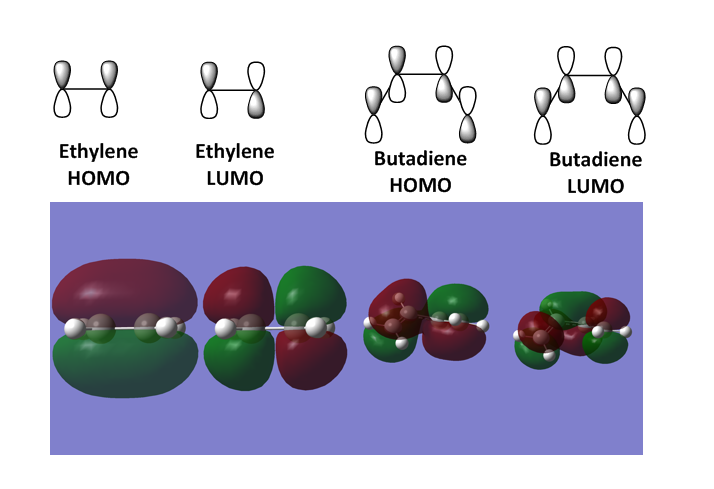
Figure 3 displays the HOMO and LUMO for both ethylene and butadiene obtained through the optimisation and frequency calculations of the two reactants. Ethylene's LUMO has one node and is asymmetric. It is the dienenophile component of this Diels Alder reaction. Butadiene's HOMO has one node and has an asymmetric symmetry. The LUMO has two nodes and is symmetric. This can overlap with the symmetric HOMO of ethylene.

Figure 4 displays the combination of the the HOMO and LUMO MO diagrams. Comparing the visualised MOs to what was expected outlined in figure 1, it can be concluded that the HOMO of ethylene and the LUMO of butadiene do interact.

Figure 3:MO diagrams for the HOMO and LUMO for Butadiene and Ethylene

Figure 4: MO diagrams for Transition State

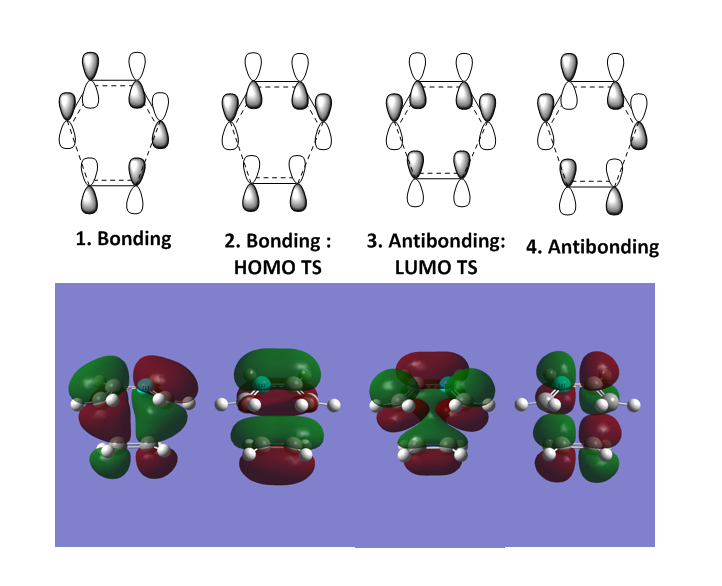
From this, the requirements for symmetry of MO to allow reactions to proceed (and not be forbidden) can be concluded. Only orbitals of the same symmetry can interact to combine. For example, the symmetric HOMO of ethylene can interact with the symmetric LUMO of butadiene. However, if the HOMO and LUMO were of different symmetry (i.e asymmetric and symmetric) this would be forbidden and the reaction would not proceed. This is due to the overlap integral being zero when orbitals of different symmetry interact and are non-zero for orbitals of the same symmetry. Table 1: Show the overlap integrals for different symmetry combinations of MOs. The overlap integral gives indication to the extent of the overlap between two orbitals (the higher this number, the more stronger the interaction). When orbitals of different symmetry interact the overlap integral is zero as there is destructive interference and no combination can occur to form an MO.

Table 1: Overlap integrals for combination of orbital symmetries

Symmetry-Symmetry of MOs	Overlap Integral
AS-AS	≠ 0
S-S	≠ 0
AS-S	0

Discussion of Changing Bond Lengths through the reaction

Table 2: Data of C-C bond lengths for the reaction

The dynamics of the reaction can also be viewed by analysing the changing bond lengths as the reaction progresses.

The table above shows the lengths of C-C bonds in the reactants, transition state and products. From this it can see the double bonds in butadiene (C1-C2 and C3-C4) lengthen over the course of the electrocyclic reaction. This is expected as the C-C single bonds are longer than C=C double bonds and this is seen as the double bond length goes from 1.33343 Å to 1.37985 Å in the TS to 1.50030 Å in the product (corresponds to a C-C single bond). This is the same for the double bond (C5-C6) of ethane which also increases in length as it forms a single bond. The single C-C bond of butadiene is the reverse of this as it is between these carbons that the double bond is formed. The length decreases throughout the course of the reaction as it goes from 1.47079 Å in the reactants to 1.41107 Å in the TS to 1.33761 Å in the final product. This again corresponds to what would be expected as the overlap of p orbitals in the double bond lead to shortening of the bond. Comparing the lengths of typical bond lengths, it can be seen that the length obtained from the optimisation and frequency calculated molecules match very closely to typical bond lengths of different hybridised C-C bond lengths. For example, a typical sp3–sp3 bond is 1.54 Å and a sp3–sp3 bond from the final product is 1.54070 Å (C5-C6). Another example is the bond length obtained for the C1-C2 bond in the product, 1.50030 Å which matches the length for a typical sp3–sp2 bond of 1.5 Å. The Van der Waals radius of a carbon atom is 1.7 Å. The length of the partially formed carbon bond in the transition state is 2.11489 Å. Hence there is overlap of the Van der Waals radius of both carbon atoms which implies the formation of the bond.

Transition State Vibrations

Figure 5: Negative Vibration for TS of reaction

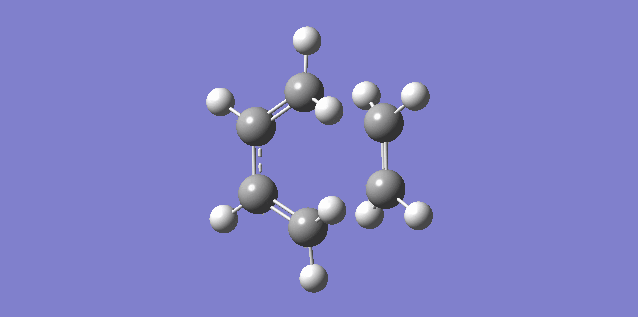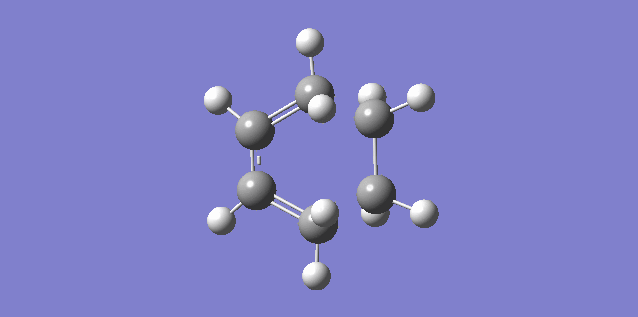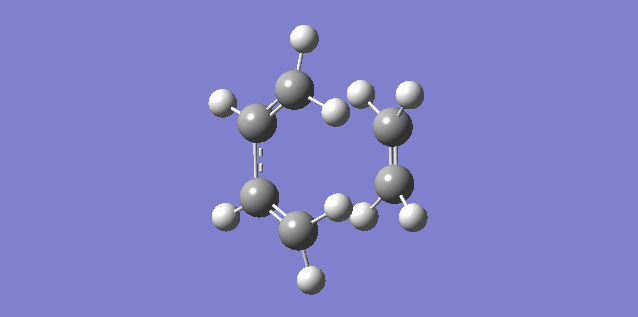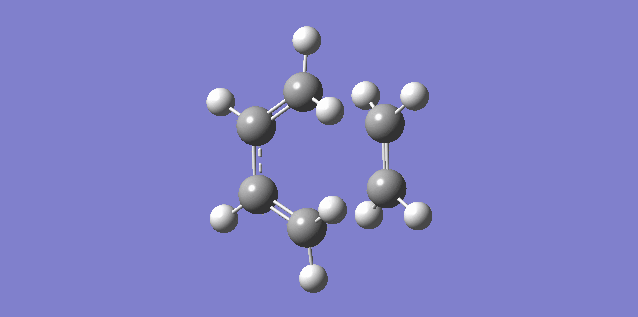
The vibration shown above in figure 5 corresponds to the imaginary vibration at -948.83. It shows the bond formation is synchronous as the components move in sync.

Figure 6: Positive vibration of Transition State

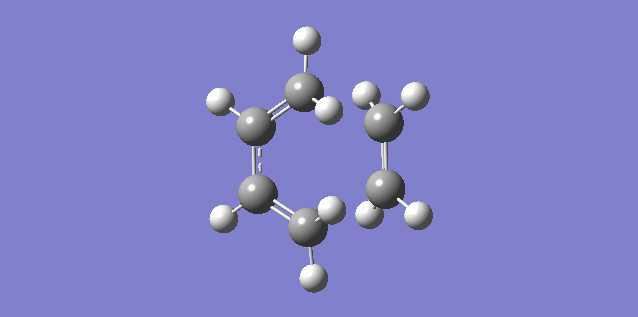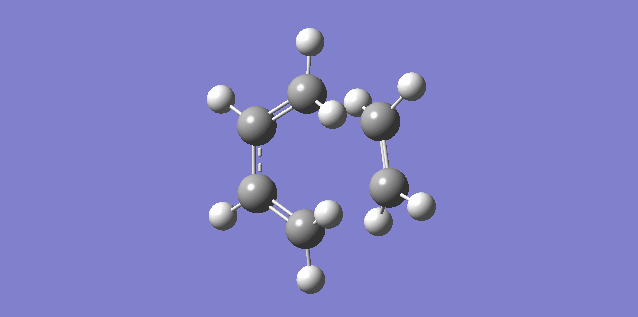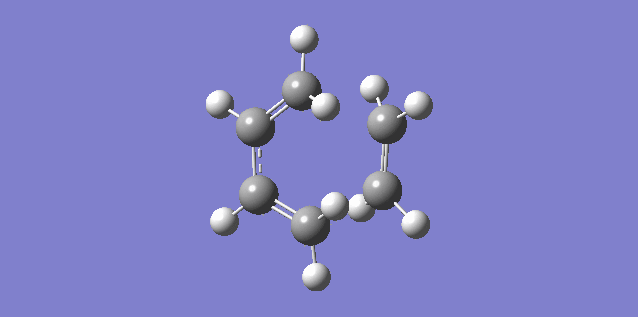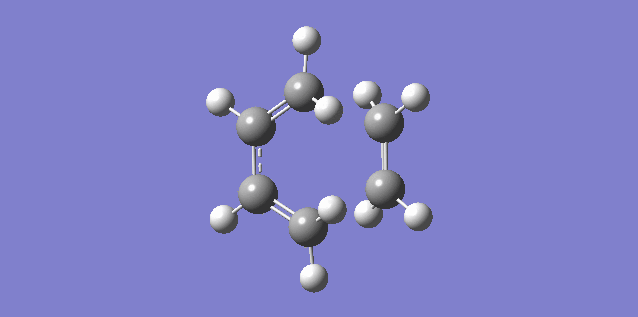
The vibration shown above in figure 6 corresponds to the lowest positive frequency at 145.14. It shows the bond formation is asynchronous as the molecules twist away from one another.

Nf710 (talk) 00:30, 20 January 2017 (UTC) Good section everything do fairly well.

Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole

Figure 7: Reaction scheme for Cyclohexadiene and 1,3-Dioxole

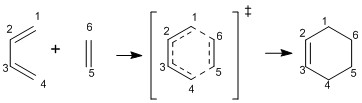
The endo and exo TSs at the B3LYP/6-31G(d) were located and used to investigate the Diels-Alder reaction between Cyclohexadiene an 1,3-Dioxole. Figure 7 shows the reaction between the reactants and the endo and exo products of the reaction.

Discussion of Molecular Orbital Diagrams

Figure 8: MO diagram for Diels-Alder reaction for Cyclohexadiene and 1,3-Dioxole

Figure 9: MOs for 1,2,3 and 4 obtained for Exo reaction

Figure 10: MOs for 1,2,3 and 4 obtained for Endo reaction

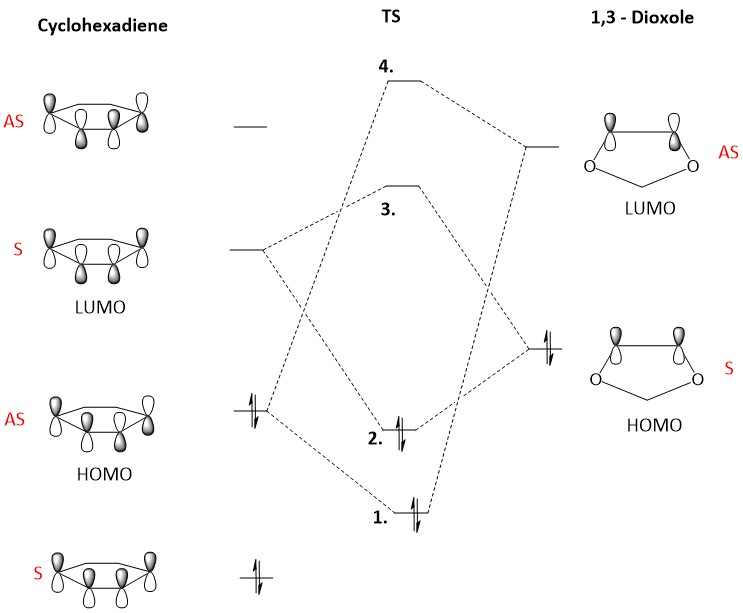
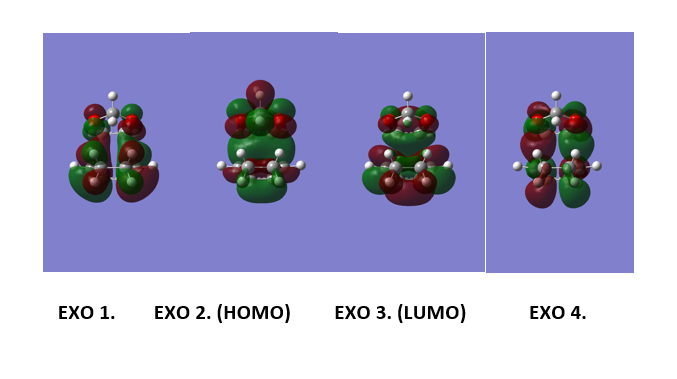
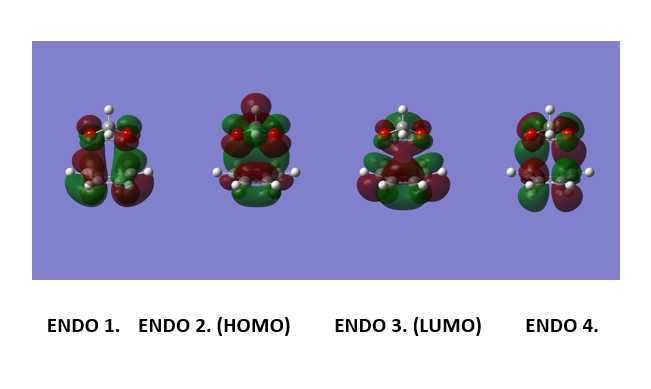
(These diagrams are a bit too small to see what's going on (bonding/anti-bonding features are important). However, symmetry is clearly visible. Tam10 (talk) 14:41, 3 January 2017 (UTC))

Figure 11: MOs homo of 1,3 dioxole and LUMO of cyclohexadiene

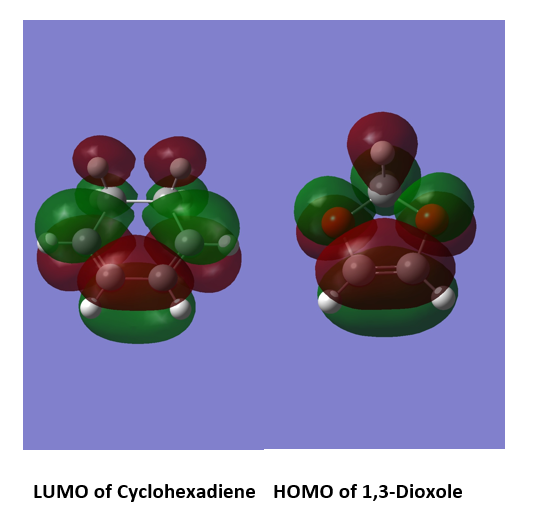
The LUMO of cyclohexadiene and the HOMO of 1,3 Dioxole interact strongly as they are close in energy. This combination results in better energetically stable bond formation. In this Diels-Alder reaction the bonding MOs which are occupied are MOs labelled as 1 and 2 in figure 8. The unoccupied antibonding orbitals are 3 and 4 in figure 8. Figure 9 shows the computed MOs for orbitals 1,2,3 and 4 for the exo reaction and Figure 10 shows the MOs computed for the endo reaction. The HOMO for 1,3 Dioxole and the LUMO (as shown in figure 11) for cyclohexadiene are both symmetric and this corresponds to an “Inverse electron demand Diels-Alder” reaction. This would be expected as hetero-Diels-Alder reactions usually proceed with inverse electron demand.

Discussion of reaction energies for Exo and Endo pathways

Table 3: Reaction energies for all Endo and Exo Pathways

	Exo	Endo
Reactants	-131377710.42	-131377710.42
Transition State	-1313614.331	-1313622.157
Products	-1313845.776	-1313849.134
Activation energies	157.08935	149.26273
Gibbs free energy	-74.35637	-77.714

Looking at table 3, it can see that the activation energy for the endo pathway is lower that the activation energy for the exo pathway. This suggests that the endo pathway which leads to the kinetically favourable product. The kinetic route is usually the endo route in Diels-Alder reactions as the secondary orbital interactions lower the energy of the transition state. The thermodynamic product in this Diels-Alder reaction is also the endo route as the product has a lower more stable energy. Usually, in Diels-Alder reactions the exo product is the thermodynamically favoured product as it exhibits less steric hinderance. However, in this example it is not the case and the endo product is the kinetic and thermodynamically favoured product.

Discussion of Secondary Orbital Interactions and Sterics

Figure 12: Secondary and Primary Orbital Interaction

Figure 13: Secondary and Primary Orbital Interaction displayed on computed MO diagrams

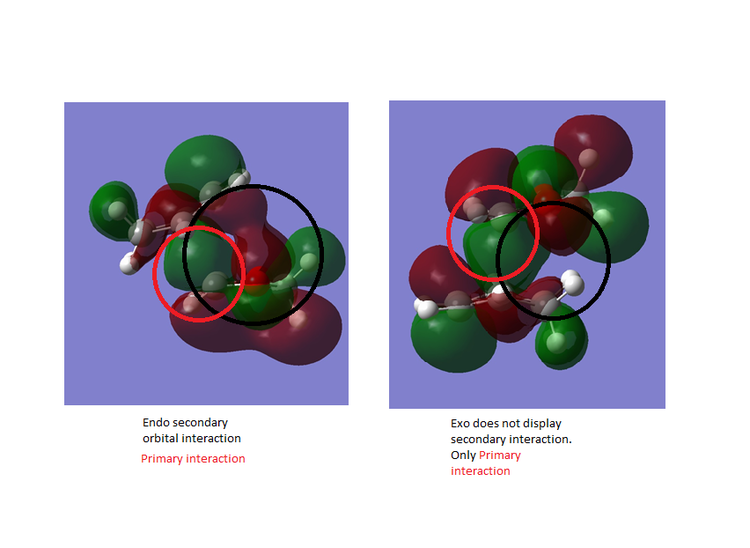
Figure 12 and 13 shows the orbital interactions observed in the reaction. The Endo pathway experiences secondary and primary orbital interaction. The secondary orbital interaction stabilises the transition state and this lowers it energy. This means that it is kinetic pathway and forms the major product if the reaction is irreversible. The HOMO of the TS for the Endo product experience secondary orbital interaction between the p orbitals of the oxygen atoms on 1,3 dioxole and the p orbitals of Cyclohexadiene. This is because of the orientation of these orbitals within the TS. The TS HOMO for the exo reaction doesn't experience any secondary orbital interactions as it does not have the correct orientation or geometry to allow this to occur. Figure 13 shows the computed HOMO for the exo and endo where the secondary and primary interactions have been outlined . The endo is the more stable product and hence exhibits less steric hindrance when compared to the endo product.

Nf710 (talk) 00:37, 20 January 2017 (UTC) EXcellent section, good understanding of a normal or inverse reaction. excellent description of SSO. Your energies however are out so I dont know what you did thee but you have still get the correct conclusion.

Exercise 3: Diels-Alder vs Cheletropic

Figure 14: Different reaction pathways for Xylene and Sulphur dioxide

Xylene and sulphur dioxide can undergo a hetero-Diels Alder cycloaddition reaction as shown in figure 14. It can occur via the endo or exo route which differ in energy and conformers of the product produced. In addition to reacting in the Diels- Alder mechanism, it can form a different product by undergoing a cheletropic reaction between the xylene and the sulphur of sulphur dioxygen, displayed in figure 14. Through computational analysis, the reaction coordinates and energies of each route has been calculated to determine the energetically preferred route.

IRC calculations for pathways

Figure 15: IRC for Cheletropic pathway

Figure 16: IRC for endo pathway

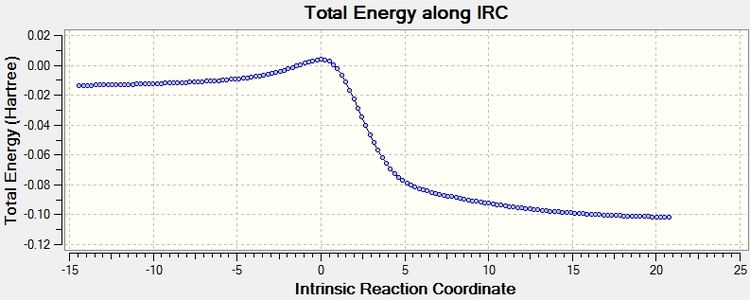
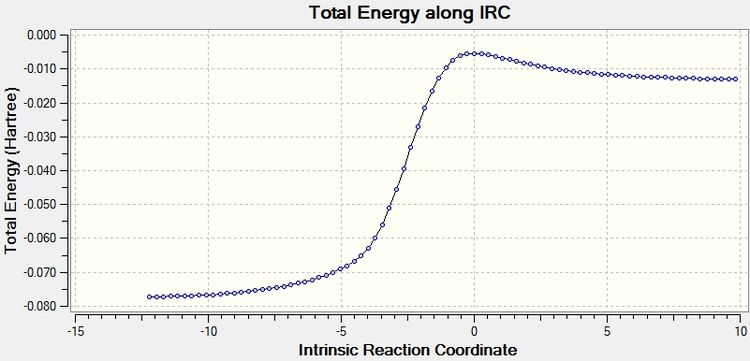
The IRC calculation appears to go from low to high but can be interpreted as starting from the products and the energy increases to reach the transition state.

Figure 17: IRC for exo pathway

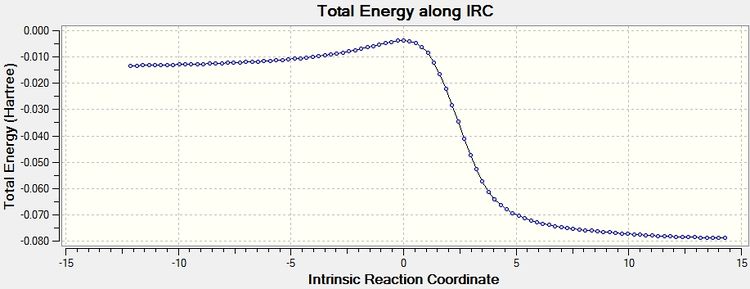
IRC starts from the transition state which has very high energy and decreases in energy to the stable products as the reaction proceeds.

Discussion of Reaction energies

Figure 18 shows energy profile diagrams for each route to the products of the reaction between xylene and sulphur dioxide from data obatined through optimisation and frequency calcultaltions (the reactants have been set to zero to aid in comparison of the different pathways).

Figure 18: Energy Profile diagrams for all pathways

(Place these on the same coordinate to make comparison easier Tam10 (talk) 14:41, 3 January 2017 (UTC))

Table 4: Reaction Energies for all pathways

	exo	Endo	Chelelotropic
Reactants	175.88	175.88	175. 88
Transition State	241.75	237.76	260.09
Products	56.33	56.97	0.72
Activation energies	65.87	61.88	84.21

It can be see from the energy profile diagram that the kinetic product (most favourable route energetically) with the lowest energy transition state is the endo Diels-Alder which is closely followed by the exo Diels-Alder. The endo Diels-Alder route was expected to have the lowest energy transition state as it exhibits stabilising secondary orbital overlap which is kinetically favourable. Provided the reaction is irreversible, this product would be the major. The least energetically favourable mechanistic route is the cheletropic but it produces the thermodynamic (most energetically stable) product.

Xylylene is highly unstable. Looking at the IRCs run for the three reactions the highly unstable xylene reactant becomes more stable as the 6-memebered ring becomes aromatic throughout the reaction.

Conclusion

The use of computation methods to optimise transition states of various pericyclic reactions to gain insight into their mechanistic pathways and energies has shown to be successful through this investigation. Through exercise 1, the PM6 method, which is a primary level optimisation was enough to give insight into the path of the reaction and to provide realistic data (i.e. on carbon bond lengths) to visualise the reaction coordinate. The higher B3LYP/6-31G(d) was used to optimise the species of both endo and exo pathways of the exercise 2 reaction. It was useful as it provided visualisations of MO to confirm the hypothesised molecular orbital combinations in the inverse electron demand Diels-Alder manner and to observe the secondary orbital interactions in the endo transition state. The optimisations were able to reveal that the endo product is both the thermodynamic and kinetic product. This information would be of great use when trying to practically conduct the experiment. Finally, the PM6 method again was used to understand the reaction between sulphur dioxide and xylene. This was able to reveal that the endo pathway leads to the kinetic product and the cheletropic pathway leads to the thermodynamic product. In addition, through observing the IRC calculation the bonding changes to xylene were able to be observed from the unstable reactant to the energetically stable product. To further improve the understanding of pericyclic reactions, further computational methods could be applied to extensive reactions. The data obtained through these optimisations (i.e. insight into major and minor products) could be correlated to practical experiment results. Furthermore, the reactions that were optimised via the PM6 method could be further optimised using a higher basis set to obtain more accurate data.