User:Rm1412

The Cope rearrangement: Optimising Reactants and Products of [3, 3]-sigmatropic rearrangement

To locate the minima corresponding to the reactants and products of the cope rearrangement on the potential energy surface of 1,5-hexadiene all the low-energy conformations of 1,5-hexadiene were considered. For initial electronic energy calculations, structures of low energy conformations were generated by varying dihedral angles A, B and C via rotation about the three central C_sp³-C_sp³ then each structure was optimised to a minimum in Gaussian using the Hartree-Fock method and basis set 3-21G (HF/3-21G). After optimisation, each structure was symmetrised to obtain the point group.

In all low-energy conformations of 1,5-hexadiene only two geometries of the four central sp³ C atoms are possible; anti and gauche. To find out which of these geometries is of lower electronic energy two 1,5-hexadiene conformers, anti 3 and gauche 4, were optimised to a minimum. Calculations using HF/3-21G level of theory show that the electronic energy of the gauche 4 conformer is lower than that of the anti 3 conformer and the difference between the electronic energies of the conformers is 0.00245 Hartree. The energy difference observed can be rationalised by the destabilisation of anti 3 due to eclipsing interactions between its C_sp²=C_sp² and central C_sp³-C_sp³ bonds, whereas these interactions are absent in gauche 4. However, the energy difference between the conformers is small (1.53740 kcal/mol) thus anti 3 and gauche 4 are of comparable stability.

Comparison of electronic energies of two 1,5-Hexadiene conformations optimised to a minimum with HF/3-21G

Conformer	1,5-Hexadiene anti 3	1,5-Hexadiene gauche 4
3D representation
Point group	C2h	C2
Electronic Energy HF/3-21G (Hartrees)	-231.68908	-231.69153
Dihedral angles (o)	A: -0.02931, B: -179.96666, C: 0.00145	A: 109.42568, B: 63.63657, C: 109.42568

Results from calculations performed with anti 3 and gauche 4 structures at HF/3-21G level of theory suggest that the lowest energy conformer of 1,5-hexadiene is one that contains a gauche linkage about the central C_sp³-C_sp³ bond. Six energetically distinct gauche conformers of 1,5-hexadiene arise due to rotation about the two C_sp²-C_sp³ bonds and optimisations using HF/3-21G level of theory were performed on the remaining five conformers in order to find the lowest energy gauche conformer. Calculations show that gauche 3 is the lowest energy conformer and this may be due to extra stability conferred from an attractive interaction between a vinyl π* orbital and the orbital of a non terminal vinyl H atom separated by 2.84021 Å, dubbed the 'C-H π' intreaction, which is not observed in any of the other gauche conformers. One conformer, gauche 2 bears a resemblance to a chair-type structure if a bond is drawn joining the terminal vinyl carbon atoms; this conformation therefore must be attained for the Cope rearrangement to proceed via a chair-like transition state.

Comparison of electronic energies of gauche 1,5-Hexadiene conformers optimised to a minimum with HF/3-21G

Conformer	3D representation	Point group	Electronic Energy HF/3-21G (Hartrees)	Dihedral angles (o)
1,5-Hexadiene gauche 1		C2	-231.68772	A: -1.59816, B: 75.76965, C:-1.57984
1,5-Hexadiene gauche 6		C1	-231.68962	A: -139.01326, B: 70.21804, C: 1.06935
1,5-Hexadiene gauche 3		C1	-231.69266	A: -117.22385, B: 67.67771, C: 120.84709
1,5-Hexadiene gauche 2		C2	-231.69167	A: 123.94083, B: -64.18194, C: 123.94083
1,5-Hexadiene gauche 5		C1	-231.68916	A: 14.23183, B: 71.05520, C: 121.13163

Three anti conformers in addition to anti 3 were optimised using HF/3-21G level of theory and none were found to have a lower electronic energy than the gauche 3 conformer thus confirming that gauche 3 is the global minimum in the conformation energy profile of 1, 5-hexadiene. The difference in energy between the anti conformers and gauche 3 can be attributed to the lack of 'C-H π' interactions in the former which are only present in the latter. A 180^o rotation about the central C_sp³-C_sp³ in conformer anti 2 results in a boat-type structure whereas in other conformers rotations about more bonds are required to attain the same type of structure.

Comparison of electronic energies of anti 1,5-Hexadiene conformers calculated with HF/3-21G

Conformer	1,5-Hexadiene anti 1	1,5-Hexadiene anti 4
3D representation
Point group	C2	C1
Electronic Energy HF/3-21G (Hartrees)	-231.69260	-231.69097
Dihedral angles (o)	A: -115.16732, B: -176.91469, C: -115.15458	A: 114.44479, B: 178.37232, C: 0.21056

To obtain a lower energy structure for the anti 2 conformer the HF/3-21G optimised structure was re-optimised using B3LYP/6-31G+ level of theory. No change in point group is observed after optimising anti 2 using B3LYP/6-31G+ and the B3LYP/6-31G+ and HF/3-21G optimised structures show no significant differences in their geometry. C_sp²=C_sp², C_sp²-C_sp³ and C_sp³-C_sp³ bond lengths, however, are shorter in the B3LYP/6-31G+ optimised structure and the energy of this structure is 1806.3303 kcal/mol lower than the HF/3-21G optimised structure.

Comparison of electronic energies of the 1,5-Hexadiene anti 2 conformer calculated with B3LYP/6-31G+ and HF/3-21G

Method	HF/3-21G	B3LYP/6-31G*
3D representation
Point group	Ci	Ci
Electronic Energy (Hartrees)	-231.69254	-234.57111
Dihedral angles (o)	A: -114.62608, B: 180.00000, C: 114.62608	A: -119.52495, B: 180.00000, C: 119.52495
Csp2=Csp2 (Å)	1.34149	1.31618
Csp2-Csp3 (Å)	1.50787	1.50882
Csp3-Csp3 (Å)	1.55532	1.55317

To confirm whether the anti 2 structure optimised with B3LYP/6-31G+ is a true minimum on the potential energy surface for 1, 5-hexadiene frequency calculations were performed on this structure at 298.15 K and 0 K with B3LYP/6-31G+ level of theory to obtain the vibrational modes and their corresponding frequencies. At both temperatures, the molecule exhibits vibrational modes with only positive frequencies thus the anti 2 structure obtained from optimising with B3LYP/6-31G+ is a minimum on the potential surface.

Comparison of IR spectra of the 1,5-Hexadiene anti 2 conformer calculated with B3LYP/6-31G+ at 0 K and 298.15 K

IR spectrum at 0 K	IR spectrum at 298.15 K

Comparison of energies of the 1,5-Hexadiene anti 2 conformer calculated with B3LYP/6-31G+ at 0 K and 298.15 K

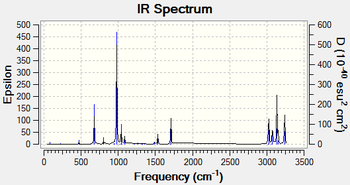
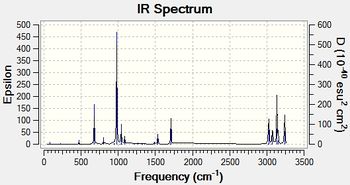
Energy quantity (Hartree/molecule)	0 K	298.15 K
Sum of electronic and zero-point Energies	(-234.428069)	(-234.428069)
Sum of electronic and thermal Energies	(-234.428069)	(-234.420763)
Sum of electronic and thermal Enthalpies	(-234.428069)	(-234.419819)
Sum of electronic and thermal Free Energies	(-234.428069)	(-234.459699)

The Cope rearrangement: Optimising Chair and Boat transition state structures

To find the preferred reaction pathway of the Cope rearrangement the activation energies for the pathways involving boat and chair like transition states must be obtained. However, due to the differences between the boat and chair transition structures different methods must be employed to optimise their structures and calculate their energies; the methods employed are outlined below. In the calculation of the activation energies for each pathway the electronic energies of conformers gauche 2 and anti 2 will be the guess for the reactant structures as these were found to possess the optimum geometries for entering the chair and boat transition states, respectively. All calculations were done at 298.15 K.

Finding and optimising the chair transition state
Three methods were employed to optimise the chair transition state structure. To generate the guess structure for the transition state an allyl radical fragment was optimised to a minimum using HF/3-21G level of theory and then two optimised allyl fragments were used to construct the chair transition state guess structure, in which the bond forming and breaking distances are set to 2.2 Å and 2.21558 Å.

Structure	Allyl fragment	Initial guess for Chair TS
3D representation
Point group	C2v	C2h
Electronic Energy (Hartrees)	-115.82304	N/A

Optimising the chair transition state
Using the guess structure, the chair transition state was optimised using the Berny algorithm and HF/3-21G level of theory. In the optimised transition state, the bond forming distances decreased, indicating the initial guess was an overestimation, and the allyl fragments had distorted.

To optimise the fragments without changing the bond forming and bond breaking distances the frozen co-ordinate method was employed. For the calculation using this method the the bond forming and bond breaking lengths were fixed at 2.2 Å and 2.21558 Å, and performed using HF/3-21G level of theory. The optimised structure obtained from the frozen co-ordinate method had distorted allyl fragments but had a higher energy than the structure obtained from optimising only with the Berny algorithm.

Using the structure optimised with the frozen co-ordinate method another frozen co-ordinate optimisation of the transition state was performed with the same algorithm and basis set as in previous chair TS optimisations and the relative positions of the atoms in each fragment fixed, allowing for adjustment of the bond forming and bond breaking lengths. This calculation resulted in a structure with similar geometrical features as those in previous chair TS optimisations but its energy was lower than that of structures obtained from the other two methods tried.

Each method produced a structure with only one negative IR frequency which corresponds to the Cope rearrangement, and have the same point group. The transition states obtained from TS Berny and Frozen Co-ordinate calculations had almost identical bond breaking and bond forming distances, which is likely due to error in setting up the guess structure. Therefore, the reaction passing through the chair TS occurs with concerted and synchronous bond breaking and bond forming at the transition state.

Method	Transition State	Point group	Electronic Energy HF/3-21G (Hartrees)	Vibration frequency corresponding to cope rearrangement (cm-1)	Bond forming and breaking distances (Å)
TS Berny HF/3-21G		C2h	-231.61932241	-817.98	2.02018 and 2.02024
Frozen Co-ordinate HF/3-21G		C2h	-231.61487984	-759.93	2.2 and 2.21558
TS Berny Frozen Co-ordinate Derivative HF/3-21G		C2h	-231.61932245	-817.96	2.02065 and 2.02070

Optimising the boat transition state
The boat transition state (boat TS) was obtained using the QST2 method and HF/3-21G level of theory, which required guess structures for the reactant and product conformations to generate the transition state. anti 2 was used as a guess for the reactant and product as this conformer had a structure closest to the boat TS, requiring only a 180^o rotation about the central C_sp³-C_sp³ to attain a boat like structure. The atoms in the reactant and product structures were renumbered to be consistent with where bond breaking and forming were expected to occur in the reaction.

Set up for QST2 calculation of the boat transition state without modifying conformer structures.

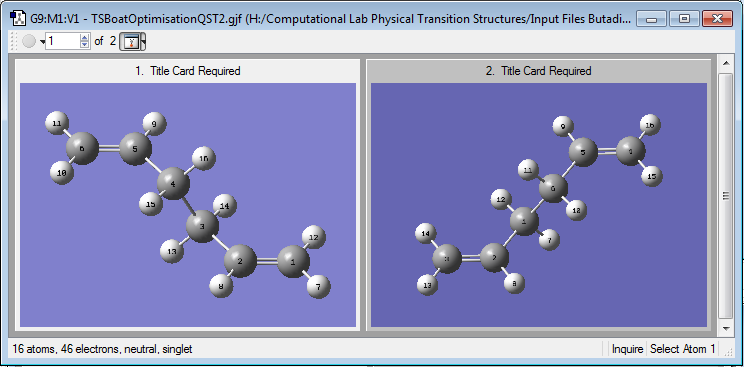
Using the anti 2 conformer as the guess for the reactants and products gives the incorrect transition state, in which the partial bonds between the fragments are crossed and appears to have a translated allyl fragment resulting in a chair-like structure. This is because the QST2 method searches for a curved path directly from the reactants to the products via one transition state and there are several possible uphill directions from the reactant minimum; hence, a transition state obtained by translating an allyl fragment, observed in this case, and one obtained from rotating the central C-C bond 180^o to form the boat-like structure are both likely outcomes of the calculation.

Method	Transition State	Point group	Electronic Energy HF/3-21G (Hartrees)	Vibration frequency corresponding to cope rearrangement (cm-1)	Bond forming and breaking distances (Å)
TS QST2 1st try		C2h	-231.61932	-817.93	N/A

To obtain a more accurate structure of the boat TS the anti 2 conformer was modified by rotating the central C-C bond 180^o resulting in a structure with eclipsing C-H and C_sp²-C_sp³ bonds. Another QST2 calculation with HF/3-21G was performed with the modified conformers as the guess for the reactant and product structures.

Set up for QST2 calculation of the boat transition state with reactants and products modified to resemble the boat transition state more closely.

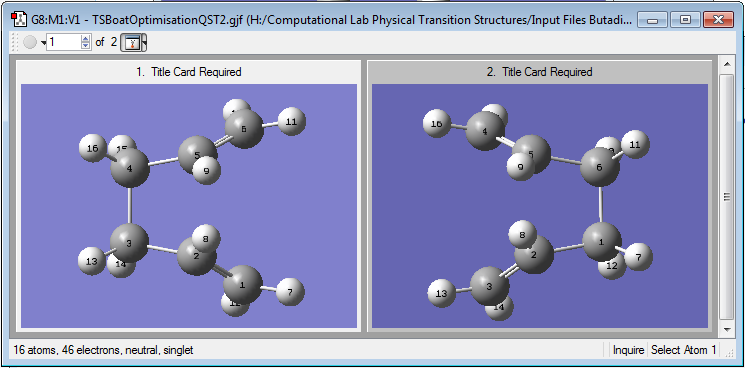
A transition state closer resembling a boat like structure was obtained using the modified conformers as the reactants and products. In the chair TS the bond breaking and bond forming distances are different by 5x10^-5 Å in the lowest energy chair TS while the difference between these distances is 8.8x10^-4 in the boat TS thus indicating bond breaking and forming is less concerted and synchronous in the latter than in the former. Only one vibrational mode with a negative frequency is observed in the boat TS, corresponding to the cope rearrangement.

Method	Transition State	Point group	Electronic Energy HF/3-21G (Hartrees)	Vibration frequency corresponding to cope rearrangement (cm-1)	Bond forming and breaking distances (Å)
TS QST2 2nd try		C2v	-231.60280	-840.01	2.14071 and 2.13983

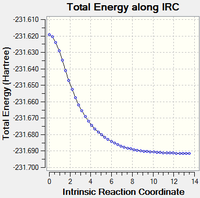
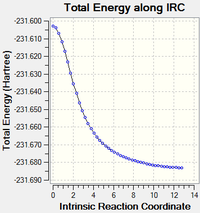
Intrinsic reaction co-ordinate of boat TS and chair TS pathways using HF/3-21G level of theory
Intrinsic reaction coordinates (IRC) were calculated for both chair and boat transition states in the forward direction of the reaction to find the product structure. Calculations were done using H/3-21G level of theory and were performed with 50 and 150 extra steps. In all IRC calculations the product minimum was reached after 44 steps starting from the chair TS and 45 steps starting from the boat TS. In the IRC starting at the chair transition state the bond breaking and forming distances are identical indicating concerted and synchronous bond formation and dissociation. The product formed is an enantiomer of gauche 2 thus showing that the reaction passing through the chair TS is energetically symmetric. The IRC starting at the boat TS leads to a product identical to the modified reactant conformer. The boat TS, unlike the chair TS, does not posses identical bond breaking and forming distances thus in this reaction pathway bond formation and dissociation is slightly asynchronous.

Transition State	IRC visualisation	IRC	Electronic Energy of transition state (Hartrees)	Electronic Energy of product (Hartrees)	Bond forming and breaking distances (Å)
Chair			-231.61932241	-231.69157850	2.02018 and 2.02018
Boat			-231.60280197	-231.68298113	2.14071 and 2.13983

TS Structure	Transition State	Product	Electronic Energy of transition state (Hartrees)	Electronic Energy of product B3LYP/6-31G+ (Hartrees)	Bond forming and breaking distances (Å)
Chair			-234.56990067	-234.51595678	2.05444 and 2.05444
Boat			-234.50423938	-234.57111	2.29201 and 2.29244

The Diels Alder Cycloaddition: [4+2] cycloaddition of butadiene and ethene

The [4+2] cycloaddition of butadiene and ethene is a normal electron demand pericyclic reaction and produces cyclohexene. In pericyclic reactions, orbital symmetry must be conserved and the excitation state of the products must be the same as that of the reactants before the reaction. Thus only orbitals of the same symmetry can overlap so that only orbitals of different symmetry will cross.

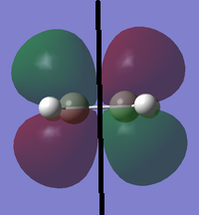
Before calculating the structures of the transition state of the [4+2] cycloaddition between 1, 3-butadiene and ethene, structures of both reactants were optimised to a minimum using Semi-Empirical AM1 and B3LYP/6-31G+, respectively. After obtaining the optimised reactant structures the symmetries of the HOMO and LUMO orbitals of each reactant with respect to a plane, defined by the black line drawn in the images below, were determined.

Structure/Orbital	Butadiene	HOMO	LUMO
3D representation
Point group/Character	C2v	Antsymmetric w.r.t. to plane	Symmetric w.r.t. to plane
Electronic Energy HF/3-21G (Hartrees)	0.04879719	-0.34381	0.01707

Structure/Orbital	Ethene	HOMO	LUMO
3D representation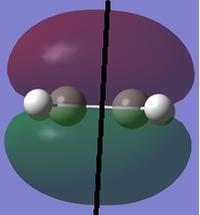
Symmetry	D2h	Symmetric w.r.t. to plane	Antisymmetric w.r.t. to plane
Electronic Energy B3LYP/6-31G+ (Hartrees)	-0.39425	-0.39425	-0.17140

From the optimised ethene and 1, 3-butadiene fragments a guess structure for the transition state was generated and three successive optimisations were performed using B3LYP/6-31G+ level of theory. The highest degree of synchronicity in bond forming and breaking is observed in the TS optimised with the frozen coordinate method in which the geometries of the 1, 3-butadiene and ethene fragments were fixed and only the bond breaking and bond forming distances were adjusted. In this TS, the bond breaking and bond forming distances are slightly less than the Van der Waals diameter of carbon (3.54 Å) and are longer than typical C_sp²=C_sp² (ca. 1.35 Å) and C_sp³-C_sp³ (ca. 1.56 Å) bonds. This suggests that the transition state has more reactant than product character and hence can be characterised as an early transition state.

Calculation+Method	Transition State	Electronic Energy B3LYP/6-31G+ (Hartrees)	Vibration frequency corresponding to cycloaddition (cm-1)	Bond forming and breaking distances (Å)
TS Berny B3LYP/6-31G+		-234.50556058	-535.92	2.25691 and 2.25817
Frozen Co-ordinate B3LYP/6-31G+		-234.50803750	N/A	2.15609 and 2.17392
TS Berny Frozen Co-ordinate Derivative B3LYP/6-31G+		-234.50556052	-536.19	2.25710 and 2.25732

Vibrational modes of the transition state obtained from the frozen coordinate (fixed fragments) method were obtained to determine the synchronicity of bond formation between the fragments. The mode with the negative frequency, corresponding to the cycloaddition, shows that both terminal ends of the ethene and 1, 3-butadiene form bonds in a synchronous fashion whereas the vibrational mode with the lowest positive frequency would suggest asynchronous bond formation.

Vibrational frequency (cm-1)	(-536.19)	136.77
3D representation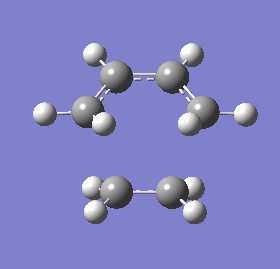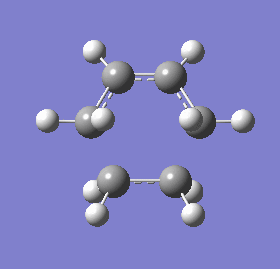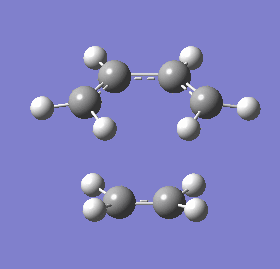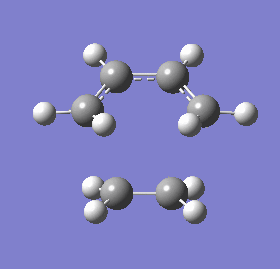

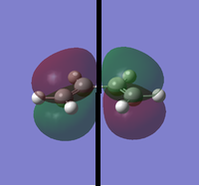
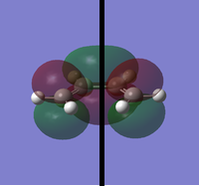
To determine whether the cycloaddition is allowed by the selection rules for pericyclic reactions the HOMO and LUMO of the transition state were generated. With respect to the plane defined by the black line in each image below the HOMO and the LUMO appear to be symmetric. Therefore, this HOMO appears to have been formed from the interaction of HOMO of ethene and LUMO of 1, 3-butadiene.

Orbital	HOMO	LUMO
View 1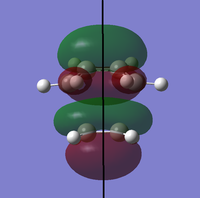
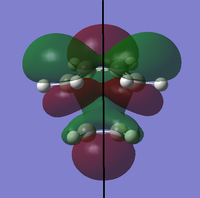
View 2
View 3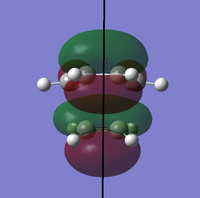
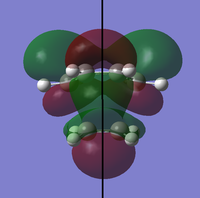
Energy (Hartree)	-0.22980	-0.02752

Molecule	1, 3-cyclohexadiene	Maleic Anhydride
3D representation
Point group/Character	C2v	C2v
Electronic Energy HF/3-21G (Hartrees)	-375.10351286	-230.53967093