User:Pp1711
Physical Module 3
Optimising the Reactants and Products
The Cope rearrangement is a [3,3] sigmatropic shift pericyclic reaction which can proceed via a chair or boat transition state. In order to determine the preferred reaction mechanism, the reactants, products and transition states have to be optimised. In this section the reactants and products will be optimised.
There are two different energy minima for 1,5 hexadiene: an anti-periplanar and a gauche conformation. In the anti-periplanar conformation the dihedral angle between the groups either side of C3 and C4 is 180 ° whereas in the gauche conformation it is 60 °. It would be expected that the anti-periplanar conformation was more stable and hence lower in energy since there would be no steric repulsion between the groups either side of C3 and C4 and no repulsion between the electrons in the pii bonds.
a) Firstly, 1,5 hexadiene was drawn in a approximate anti-periplanar conformation so that the groups either side of C3 and C4 were in a anti-periplanar arrangement. The structure was then cleaned and optimised to a minimum using HF/3-21G method and basis set. The output file was then symmetrized and the molecule was found to have a point group of C1. The energy of this conformation was -231.6909 a.u. Guess anti-periplanar conformation
b) Similarly, a gauche conformation of 1,5 hexadiene was drawn, cleaned and optimised to a minimum using HF/3-21G method and basis set. The point group was also C1 and the conformation had a energy of -231.68916020 a.u. The gauche conformation was found to be higher in energy by 0.0017398 a.u confirming that it is a higher energy conformation. Hexadiene gauche conformation
c/d) Having concluded that the anti-periplanar conformation is the lowest energy conformation, another anti-periplanar conformation was drawn trying to make all the carbons either side of C3-C4 anti-periplanar. The input file was as shown:Hexadiene anti peri-planar However, on optimisation to a minimum it was found to have an energy of -231.69266122 a.u and correspond to gauche 3 in Appendix one. After symmetrizing if had a point group of C1. The structure is lower in energy than the guess anti-periplanar and gauche conformations. Hexadiene anti-periplanar output The structure was further optimised using DFT method and BY3LP/6-31G* basis set to give an energy of -234.61132934 a.u.
e) Having not previously located the Ci anti2 conformation, it was drawn and optimised using HF/3-21G method and basis set. To ensure that the correct conformation was obtained, the energy and point group were compared to Appendix 1. The conformation was found to have a energy of -231.69253528 a.u. which corresponds to the energy of the Ci anti2 conformation in Appendix 1, which reports an energy of -231.69254 a.u. On symmetrizing, the point group was confirmed to be Ci without relaxing any criteria. Thus, from the energy and point group it was concluded that the correct conformation had been obtained. Ci anti2 conformation
On trying to reach this conformation, the anti4 conformation was also found and can be viewed below. Anti4 conformation This had an energy of -231.69097055 a.u.
f) The Ci anti2 conformation was then further optimised to a minimum using a higher method and basis set. It was optimised to a minimum using DFT and B3LYP/6-31G* method and basis set.The energy of the conformation was found to be -234.61170282 a.u. Using a higher level of theory provides more accurate results: compared to the HF/3-21G optimised conformation, this was found to be -2.9207775 a.u lower in energy. On comparing the optimised Ci anti2 conformations, they appear to look the same. B3YLP.6-31G* Ci anti 2 conformation
| ' | HF/3-21G | B3LYP/6-31G* |
| Electronic Energy (a.u) | Electronic Energy (a.u) | |
| Gauche 3 | -231.6926612 | -234.6113293 |
| Anti 2 | -231.6925353 | -234.6117028 |
Table to summarise anti2 and gauche3 conformations
Whilst under HF/3-21G, the gauche3 conformation is lower in energy than the anti2 conformation, but when optimised to higher levels of theory (B3LYP/6-31G*), the anti2 conformation is lower in energy by 0.00037348 a.u. and hence the most stable conformation overall.
g) In order to confirm that the conformation was a minimum a frequency calculation was carried out. 'Frequency' was selected under the method type, and the frequency calculation carried out under DFT,B3LYP/6-31G* method and basis set. After opening the log file, and checking 'Vibrations' it was confirmed that this was a minimum point on the potential energy curve as all frequencies were real and positive. An IR of the molecule can be viewed:
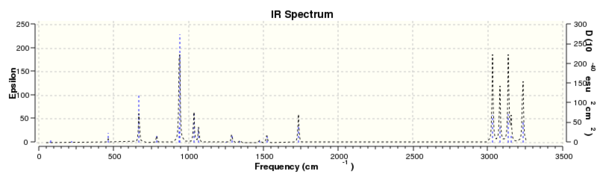
From the output file, Thermochemistry data could be obtained.The following was recorded:
| Thermochemistry Data | Energies (a.u) |
| Sum of electronic and zero-point Energies | -234.469212 |
| Sum of electronic and thermal Energies | -234.461856 |
| Sum of electronic and thermal Enthalpies | -234.460912 |
| Sum of electronic and thermal Free Energies | -234.500821 |
Therefore using the energy of the 1,5 hexadiene individual energies and enthalpies were calculated:
| Thermochemistry Data | Energies (a.u) |
| Zero-point energy | 0.1424908 |
| Thermal Energies | 0.1498468 |
| Thermal Enthalpy | 0.1507908 |
| Thermal Free Energy | 0.1108818 |
Summary of anti2 energies:
| ' | HF/3-21G | ' | ' | ' | B3LYP/6-31G* | ' | ' |
| Electronic Energy (a.u) | Sum of electronic and zero point energies (a.u) | Sum of Electronic and thermal energies (a.u) | Electronic Energy (a.u0 | Sum of electronic and zero point energies at 0K (a.u) | Sum of Electronic and thermal energies at 298K (a.u) | ||
| Reactant (anti2) | -231.6925353 | -231.53954 | 231.532566 | -234.6117028 | -234.469212 | -234.461856 | |
Optimising the Chair and Boat transition structures
In order to calculate the activation energy for the chair and boat transition structures from the optimised reactant/product, the chair and boat conformations also need to be optimised as transition states. In this section, both the chair and boat transition states are drawn and optimised. To confirm these transition states lead to the correct product, a frequency calculation was carried out and a intrinsic reaction co-ordinate was also run to ensure the transition state lead to the correct product. Finally, the activation energies were calculated.
a) Firstly, a guess chair transition state was drawn. An allyl fragment, C3H5, was drawn, cleaned and optimised as a transition state under HF/3-21G level of theory. It had a energy of -118.823040010 a.u.
The optimised structure was then copied and appended in a new molecule window twice. The fragments were then positioned so that they resembled a chair transition state. The distance between the terminal ends of the allyl fragments were checked to be 2.2A using the builder toolbar. This structure was saved and then copied and appended into another new window.
For the chair transition state two different methods of optimising a transition state were explored : firstly a optimisation as a transition state with a frequency calculation to show that a transition state had been reached with the force constant determined at the beginning, and secondly, the Redundant Co-ordinate method.
b) The chair transition state was then optimised as a transition state (TS Berny) under HF/3-21G, computing the force constant once. Opt+Freq was selected under method so that a frequency calculation could also be run. Additional key words were 'Opt=NoEigen' so that the system would not crash if more than one imaginary frequency was detected suggesting the transition state guess structure differs a lot from the actual transition state. After running the calculation,the structure was found to have an energy of -231.61932232 a.u. On opening the 'Vibrations' one imaginary frequency of -817.86cm-1 was found. As only one imaginary frequency was found, the transition state is a good approximation of the actual transition state, and secondly, the presence of an imaginary frequency confirms that the structure is a transition state: the curve is at a maximum on the potential energy surface. An image of the optimised chair transition state and the imaginary vibration can be viewed below. Chair transition state optimised
The bond lengths of the forming sigma bonds are 2.02083A (top) and 2.02063A (bottom).
c) The chair transition state from part a was then appended in a new window and optimised via the Redundant Co-ordinate method. The guess transition structure was opened and the bond length between the bond forming carbons was checked to be 2.2A. Then from the edit menu, Redundant Co-ordinates was selected. The pair of carbon atoms that would form the bonds were selected and 'Bond' instead of 'Unidentified' and 'Freeze Co-ordinates' instead of 'Add' were selected. This was repeated for the second pair of carbons forming the other sigma bond. The calculation was then run, optimising to a minimum under HF/3-21G. Frozen co-ordinate transition state The energy of the transition state with frozen bond lengths was -231.61427839 a.u with a dipole moment of 0.0015.
d) Next, the bond lengths were optimised, unfrozen. From the Redundant Co-ordinates menu the pairs of carbons were selected as before but this time, 'Bond' instead of 'Unidentified' and 'Derivative' instead of 'Add' were selected. A transition state optimisation was then run with the force constant never calculated. The checkpoint file would not open and after several attempts, the log file was opened instead successfully. Unfrozen chair transition state optimised As the bond lengths were no longer fixed to 2.2A, it was found using the builder toolbar, that the bond lengths between the forming bonds were 2.19891A (top) and 2.26073A (bottom). The energy of the unfrozen molecule was -231.56145001 a.u. The transition states looks similar to the transition state from part b although the partially forming bond lengths are different as they are no longer frozen and the energy is also higher. Since the partial forming bond lengths are slightly different this suggests concerted bond formation characteristic of pericyclic reactions.
The transition state was confirmed by carrying out a frequency calculation. One negative frequency of -723.95cm-1 was found and is shown below:
This is a similar animation to that in part b, as both are undergoing the Cope rearrangement, however in this animation (unfrozen) the interaction is stronger. On optimisation under B3LYP/6-31G* the partially forming sigma bonds lengths were 1.96702A and 1.96637A.
e) Having optimised the chair transition state in two different ways, optimising as a transition state and the frozen/unfrozen method, for the boat transition state, the QST2 method was used. This methods involves stating the reactants and products and then finding the transition state that links them. Firstly, the Ci anti-periplanar conformation reactant molecule from part one was opened as a checkpoint file. The molecule was appended into a new window twice:these were the reactants and products. The numbering of the atoms were changed so that the reactant corresponded to the product if it had been arranged. The calculation was run as a Opt+Freq and optimising to a transition state, TS(QST2). Opening the chk file produced this structure: Original QST2 transition state optimised This structure resembled a chair more than a boat and so this is incorrect.
The bond angles between the four central carbon atoms (C2-C3-C4-C5) was set to 0 degrees whilst the bond angle between first three carbon atoms on either side (C1-C2-C3 and C4-C5-C6) was set to 100 degrees. This was repeated for the products. The calculation was run again and an energy of -231.60280212 a.u was obtained with a dipole moment of 0.1588 and from the log file, one imaginary frequency of -840.41cm-1. Boat transition state This transition state resembles a boat and it can be confirmed that it is indeed a transition state as only one negative frequency is observed.
Animation of the imaginary stretch:
The partially forming bond lengths are 2.13901A (top) and 2.13944A (bottom).
| ' | HF/3-21G (a.u) | B3LYP/6-31G* (a.u) |
| Reactant (anti2) | -231.6925353 | -234.6117028 |
| Boat TS | -231.6028021 | -234.5430931 |
| Chair TS (ts berny) | -231.6193223 | -234.556983 |
| Chair TS (frozen co-ord method) | -231.56145 | -234.5569828 |
Table to summarise energies of transition states.
Comparing the energies of the optimised boat and chair transition states at B3LYP/6-31G* it can be concluded that the boat is a higher energy transition state. It is 8.716045705 kcal/mol higher in energy compared to the chair transition state optimised with force constants calculated at the beginning and 8.715920203 kcal/mol higher than the chair transition state from the redundant co-ordinate method.
f) An intrinsic reaction co-ordinate, IRC, was run to determine which conformation the optimised chair transition state lead to by following the minimum energy path. The optimised chair from the TS(Berny)optimisation was used. IRC was selected under Job Type, force constant calculated always, N=50 and computed in one direction only as the reaction co-ordinate is symmetrical. The optimised chair transition state from part b was used.
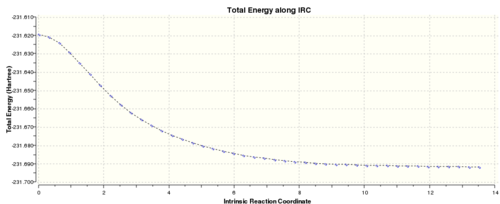
IRC of chair transition state
The final point on the IRC had a energy of -231.69157913 a.u, RMS of 0.00015224, and a dipole moment of 0.3631. After symmetrizing it had a point group of C1.Final structure on the IRC The bond distance between the terminal carbons was 4.23214A.
Then, the structure corresponding to the final co-ordinate, number 44, was optimised to a minimum. This structure had a energy of -231.69166702 a.u, RMS gradient of 0.00000474, dipole moment of 0.3806 and after symmetrizing, a point group of C2. The distance between the terminal carbons was found to be 4.39012A. The optimised chair transition state lead to a gauche2 conformation. Both the energy and point group correspond to this conformation in Appendix one. Minimised product
Similarly, an IRC was carried out on the boat transition state to determine what product it lead to. The final point on the IRC was minimised. The energy of the final minimised structure was -231.69266121 a.u. and after symmetrizing it had a point group of C1. This corresponds to the gauche3 conformation in the Appendix. Minimised product from boat transition state
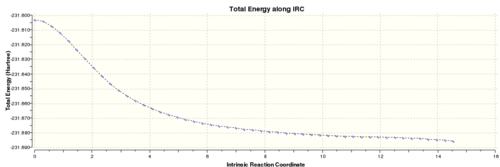
IRC of boat transition state
g) The activation energies of the reaction via chair and boat transition structures were then calculated using the optimised 1,5 hexadiene anti2 conformation as the reactant. The chair and boat transition structure were optimised from HF/3-21G to B3LYP/6-31G*, a higher level of method and basis set, and frequency calculations were also carried out. The calculation results are shown below.
| ' | HF/3-21G (a.u) | HF/3-21G (kcal/mol) | B3LYP/6-31G* (a.u.) | ' | B3LYP/6-31G* (kcal/mol) |
| Ea for boat | 0.08973316 | 56.30842006 | 0.06860975 | 43.05327733 | |
| Ea for chair (TS Berny) | 0.07321296 | 45.94183583 | 0.05471979 | 34.33719397 | |
| Ea for chair (frozen method) | 0.0547198 | 34.33720025 | 0.05472007 | 34.33736968 | |
Re-optimised chair B3LYP/6-31G*
Re-optimised boat B3LYP/6-31G*
Comparing the energies and geometries of the transition states at different methods and basis sets it can be concluded that the energies differ but the geometries look similar. The chair transition state was optimised in two different ways and the energy difference between the activation energies from the two different methods is 0.000175703 kcal/mol; this is a very small difference in energy.
Frequency calculations were then performed so that Gaussian 09 could be used to determine Thermochemistry data at different temperatures.
| Boat transition state | ' |
| Temperature (K) | Thermal correction (a.u) |
| 298 | 0.133314 |
| 100 | 0.127810 |
| 50 | 0.127225 |
| Chair | ' |
| Temperautre (K) | Thermal correction (a.u.) |
| 298 | 0.134642 |
| 100 | 0.128753 |
The activation energies:
Boat: 43.05 kcal/mol +/- 0.13
Chair (TS Berny): 34.34 kcal/mol +/- 0.13
Comparing these energies to the literature values of 33.5 ± 0.5 kcal/mol (chair) and 44.7 ± 2.0 kcal/mol (boat) at 0K, at 298K the activation energies are higher. The difference between the chair transition states at the two temperatures is 0.84 kcal/mol whilst the difference in the boat transition states is 1.65kcal/mol.
Diels Alder Cycloaddition
i) Cis butadiene was drawn, cleaned, and optimised to a minimum using the AM1 semi-empirical molecular orbital method. The strucure was found to have a energy of 0.04879720 a.u, dipole moment of 0.0415, and RMS gradient of 0.00002543.
Optimised cis butadiene
After symmetrizing it had a point group of C2v.
Symmetrized cis butadiene
The HOMO and LUMO were then visualised by going to Edit, MOs, selecting the HOMO and LUMO and clicking on visualise, then update.
HOMO with an energy of -0.34381 a.u:
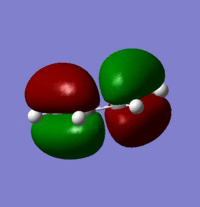
LUMO with an energy of 0.01708 a.u:

Looking at the MOs it is possible to determine their symmetry. The HOMO is anti-symmetric with respect to the plane whilst the LUMO is symmetric with respect to the plane.
The cis-butadiene was optimised using HF/3-21G and BY3LYP/6-21G* methods and basis sets in subsequent calculations.
ii)
Computation of the Transition State geometry for the prototype reaction and an examination of the nature of the reaction path.
In this section the aim was to determine the transition state for the reaction between ethylene and cis-butadiene and confirm it lead to the correct product.
The guess transition state of the reaction was drawn and cleaned: Guess transition state. The distance between ethylene and butadiene was set to 2.2A as the distance is usually 2.1-2.3A between partially forming bonds in the transition state.
The following calculation was then run: Opt+Freq, optimising to a transition state. The method used was AM1 semi empirical. An energy of 0.11165468 a.u, RMS = 0.00001583, Dipole moment of 0.5604 was obtained. Optimised guess transition state Length of sigma forming bonds: 2.11937A (top) and 2.11937A (bottom).
The vibrations contained one imaginary frequency of -956.16 cm-1 which is shown here:
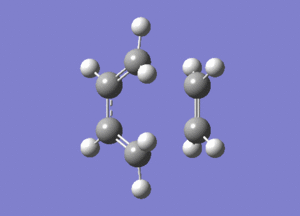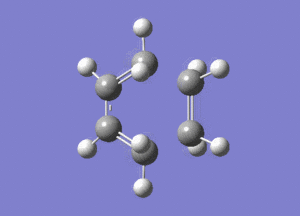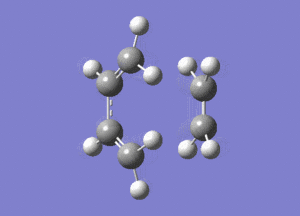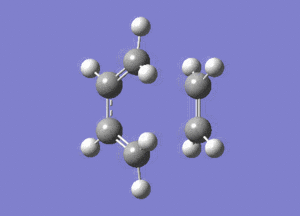
The method chosen to optimise the transition state was the frozen co-ordinate method. This was done in the same way as in part 2, freezing the bond lengths at 2.2A and optimising to a minimum, followed by relaxing the molecule and optimising to a transition state. It should be noted that freezing the bond lengths at 2.2A was achieved by fixing the atoms.
The frozen co-ordinates gave an energy of 0.10745405 a.u and RMS of 0.00618468. Frozen transition state of the log file
Then the co-ordinates were unfrozen and optimisation to a transition state was performed. The resultant energy of the transition states under AM1 semi-empirical basis sets was 0.11165488 a.u with an RMS of 0.00002868. The sigma forming bonds lengths were 2.11874A (top) and 2.11968A (bottom). Unfrozen transition state
In order to confirm that the conformation was a transition state and to confirm it was the reaction path for the reaction, a frequency and IRC calculation was carried out.
An imaginary frequency of -956.31cm-1 was found and the vibration is shown here:
. This confirms it is a transition state. This animation shows that the formation of the bonds is a synchronous concerted process. The first positive vibration with a frequency of 147.07cm-1 is modeled here:
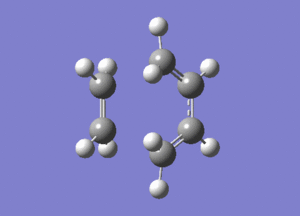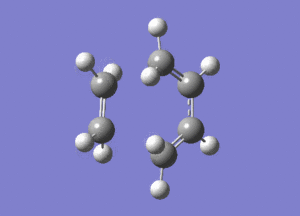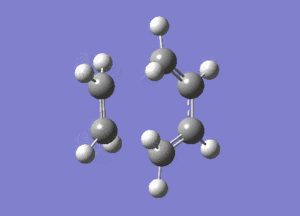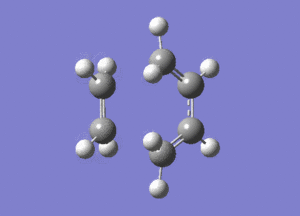
. This vibration suggests bond formation to be a asynchronous process.
Running the IRC as in Part two, but this time in both directions as the reaction is not symmetrical, the following profile was obtained:
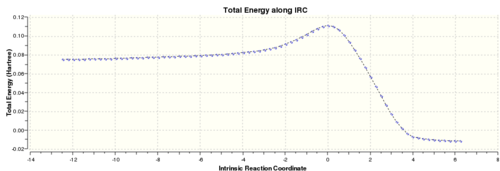
1st co-ordinate (reactants): Reactants Energy= 0.07535676 a.u. RMS=0.00018607 Dipole Moment=0.0349
76th co-ordinate (product): Product Energy = -0.01099181 a.u RMS = 0.00009803
However a frequency calculation on the 76th co-ordinate showed a imaginary frequency of -34.29 cm-1.
. This suggests that the curve has not yet plateaued and reached a minimum surface.
Therefore, the 76th co-ordinate was optimised to a minimum with force constants never calculated. The resulting structure had a energy of -0.01619485 a.u and RMS of 0.00003478. Minimised product. A subsequent frequency calculation was performed and no imaginary frequencies were present, concluding that the product had been obtained. No negative frequencies are possible as reactants and products are at a minimum on the potential energy curve.
Having confirmed that the transition state was a transition state and lead to the desired product, the HOMO and LUMO were visualised.
HOMO energy under AM1 semi-empirical:-0.32394 a.u.
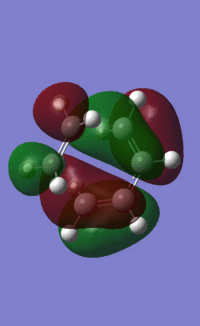
LUMO energy under AM1 semi-empirical= 0.02316 a.u.
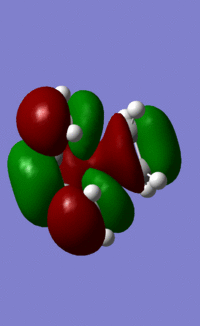
The HOMO is anti-symmetric with respect to the plane of symmetry whilst the LUMO is symmetric with respect to the plane of symmetry. The LUMO of ethylene combines with the HOMO of butadiene to form the HOMO. This is because from the HOMO it can be seen that the ethylene molecular orbitals are anti-symmetric and are therefore the LUMO of ethylene. Therefore in order to be allowed the LUMO of ethylene must combine with the HOMO of butadiene which is also anti-symmetric, as only orbitals of the same symmetry can overlap.
Once it had been confirmed that the transition state had been located, the reactants, product and transition state were optimised from AM1 semi-empirical to HF/3-21G and then B3LYP/6-21G*. The results are summarised in the table below:
| Method/Basis set | Reactants Energy (a.u.) | Transition state energy (a.u) | Bond forming lengths (A) | Imaginary frequency (cm-1) | Product energy (a.u) |
| AM1 Semi Emperical | 0.07535676 | 0.11165488 | 2.11874 (top) 2.11968 (bottom) | -956.31 | -0.01099181 |
| HF/3-21G | -231.658063 | -231.6032086 | 2.20956 (top) 2.20957 (bottom) | -818.36 | -231.720374 |
| DFT BY3LP/6-31G* | -234.5754296 | -234.5438965 | 2.27237 (top) 2.27237 (bottom) | -524.63 | -234.63915436 |
From the highest basis set, BY3LP/6-31G* the imaginary vibration is shown:
Imaginary Vibration:
The distance between the partially forming sigma bonds of the optimised transition state under DFT, BY3LP/6-31G* was 1.54930A and 1.54936A.
Typically, sp3 bond lengths are 1.54A and sp2 bond lengths 1.47-1.48A. [1] The van der waals radius for a carbon atom is 0.8A.[2] The partially forming bonds are longer than the double bond length which is to be expected and slightly longer than single bond length. At the transition state the bond has not formed therefore, there are attractive van der waals interactions between butadiene and ethylene which will bring the molecules closer together for bond formation.
iii) In this section the regio-selectivity of the reaction between maleic anhydride and cyclohexa-1,3-diene was considered. Two products can form: the endo or the exo product. The endo product is the kinetic product with a lower energy transition state.
Firstly, cyclohexa-1,3-diene was drawn, cleaned and optimised under the Semi Empirical AM1 method and basis set.Cyclohexa-1,3-diene optimised. Energy= 0.02771129 a.u. RMS= 0.00000562 After symmetrizing the molecule had a point group of C2.
Maleic anhydride was drawn, cleaned and optimised: Maleic anhydride optimised. Energy= -0.12182418 a.u. RMS=0.00003683 After symmetrizing it had a point group of C2v.
The exo product was drawn, cleaned and optimised: Exo product. Energy= -0.15990935 a.u. RMS= 0.00002559
The QST2 method was used to identify the transition state. As before, the atoms were labelled and the QST2 calculation run.
Exo transition state.
Energy of transition state located by QST2 method= -0.05041979 a.u RMS= 0.00002729 Dipole moment= 5.5642
After running a frequency calculation the transition state was confirmed as only one imaginary frequency of -812.33cm-1 was found.
The bond formation appears to be a synchronous process.
This method shows that having specified the reactants and products, the maximum point on the curve that links them is the transition state. To confirm this, an IRC was run on the exo transition state in both directions with N=50.
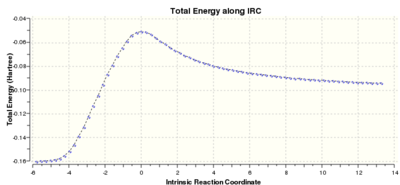
The energy of the product was -0.15990910 a.u with an RMS of 0.00001040. Exo product. The bond lengths of the sigma bonds that are formed in the reaction were both 1.53613A. The product was then further optimised to a minimum to give an energy of -0.15990911 and a RMS of 0.00005068. The bond lengths of the sigma bonds formed were 1.53619A (top) and 1.53620A (bottom). Final exo product
Having confirmed the transition state, the MOs of the transition state were viewed. The HOMO and LUMO under B3LYP/6-31G* are shown below:
HOMO:
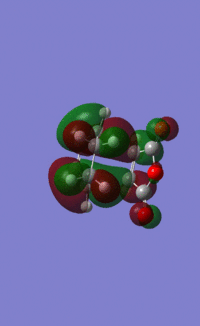
LUMO:
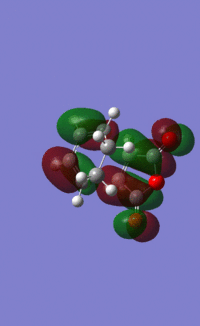
Endo product:
For the endo product the QST2 method was also used.
The endo product was drawn, cleaned and optimised under Semi-empirical AM1. Endo structure. Energy of endo product= -0.11146904 a.u. RMS = 0.00003134 Dipole moment = 5.6084
Following the same procedure as above, the atoms were labelled, the bond lengths of the partially forming bonds was fixed to 2.2A. From the frozen method the energy was -0.05238778 a.u, RMS = 0.00270713, dipole moment= 5.9987.
Then the unfrozen molecule was optimised to a transition state and yielded an energy of -0.05150479 a.u, RMS = 0.00001078 and dipole moment of 6.1663. The bond length of the partially forming sigma bonds was 2.16234A (top) and 2.16242A (bottom) Endo unfrozen final.
From a frequency calculation, a imaginary frequency of -806.36 cm-1 was obtained:
This confirmed that a transition state had been found as only one imaginary frequent was shown.
IRC:
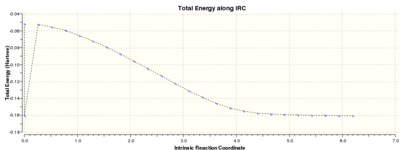
The IRC shows that the correct product is made from the endo transition state although the second point has the same energy of the product. The Chk file could not be opened, and this is the result from the log file. Despite the unexpected minimum point, the curve plateaus to a minimum and the endo product has an energy of -0.16017077 a.u. The calculation was re-attempted several times however without success. Endo product.
The MOs of the endo transition state under B3LYP/6-31G* were also visualised:
HOMO:
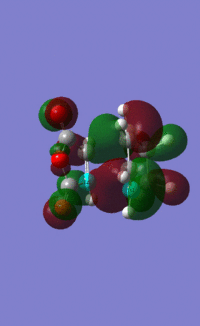
LUMO:

For both the endo and exo transition states, the calculations were run from AM1 semi empirical, to HF/3-21G and then DFT, BY3LP/6-31G*. The results are summarised in the tables below:
| ' | Energy of Exo TS (kcal/mol) | Energy of Endo TS (kcal/mol) |
| AM1 Semi Emperical | -31.63890266 | -32.31975058 |
| HF/3-21G | -380022.0722 | -380026.3248 |
| DFT BY3LP/6-31G* | -384462.1542 | -384464.718 |
Comparing the energies of the DFT, B3LYP/6-31G* optimised transition states, the exo transition state has a energy of-384462.1542 kcal/mol whilst the endo transition state has an energy of -384464.718 kcal/mol. The endo form is lower in energy by 2.563816 kcal/mol. In the exo form, the distance between the CH2-CH2 on the cyclohexa-1,3-diene and the (C=O)-(C-O)-(C=O) on the maleic anhydride is 2.94504A, whilst in the endo form the separation is 3.89657A and 3.89735A.
The secondary orbital overlap effect is the stabilising interaction caused by the overlap between the p orbitals on C=O on the maleic anhydride and the p orbitals on the cyclohexa-1,3-diene. This secondary interaction is present in the endo form but not the exo, hence the endo transition state is stabilised and is the kinetic product. [3] Studying the HOMO of the exo transition state, it can be concluded that there is no interaction between the p orbitals of the maleic anhydride and the p orbital of the cyclohexa-1,3-diene since they are not orientated to interact with each other.
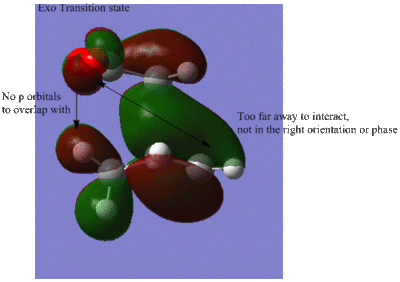
Looking at the HOMO of the endo transition state, there is a secondary interaction however it appears at first instance to be to be negative, anti-bonding. However on orientation of the molecule, there is a some positive overlap between the p orbitals of C=O and p orbitals of the cyclohexa-1,3-diene. This is shown in the diagrams below.

Therefore the endo product has an extra stabilsing interaction and this lowers the energy of the transition state resulting in the endo product being the fastest forming kinetic product. The stabilsing interaction outweighs the strain which would otherwise increase the energy of the endo transition state. The exo product is thermodynamically more stable but as it does not undergo secondary interactions, it is has a higher energy transition state.
Allen, F.H (1997). "Bond Lengths in Organic Compounds". J. Chem. Soc 11: missing pages. [1].
Batsanov, S.S (2001). "Van der Waals Radii of Elements". Inorganic Materials 37(9): 871-885. [2].
Fox, M.A, Cardona, R, Kiwiet, N.J (1986). "Steric Effect v Secondary Orbital Overlap in Diels Alders Reactions. MNDO and AM1 studies". J.Org.Chem missing volume: 1469-1474. [3].
