User:Pb1712

Introduction

The aim of the experiment is to analyse the transition structures of certain rearrangements and reactions using GaussView. The experiment will explore different calculation methods.

Cope Rearangement

In this exercise a [3,3] sigmatropic shift is analysed. DOI:10.1021/ed084p2001 The reaction occurs intramolecularly where two double bonds are separated by 3 sigma bonds. The reaction can be seen under figure 1 with a 1,5 diene which will be the structure analysed. The rearrangement is a concerted pericyclic reaction that passes through a bi-radical transition state similar in structure to two ally fragments. DOI:10.1021/ja00101a078

In Gauseview an anti periplanar conformation (for the four central carbon atoms) was drawn of 1,5 – hexadiene. The structure was cleaned and optimised using HF/3-21G level of theory. Figure 2 displays the optimised structure of the conformation with its corresponding energy and point group.

Input Structure	Optimised Structure	Energy (A.U.), Symmetry Label
		-231.69260, C2

Figure 2: An Input and Optimised structure of 1,5 – hexadiene with its corresponding Energy and point group

Various conformations are tested by altering the geometry of 1,5 - hexadiene to acquire different Gauche and A.P.P. conformations. The above method is repeated to attempt to locate the lowest energy conformer. Table 1 summarises the conformations found by through this process.

Conformer	Energy (A.U.)	Point Group
Anti 1	-231.69260	C2
Anti 2	-231.69254	Ci
Anti 3	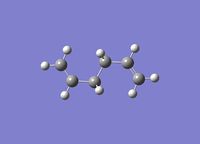-231.68907	C2h
Gauche 1	-231.69167	C2
Gauche 2	-231.69266	C1
Gauche 3	-231.68907	C1

Table 1: Summary of Conformers found and the corresponding energies and point groups using HF/3-21G level theory

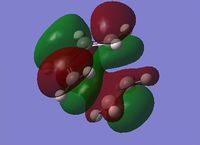
It may be thought that the global minimum conformation would have an A.P.P. relationship between the four central carbons similar to that of butane. Butanes staggered A.P.P. conformation is lower due to the stabilising orbital interactions of sigma CH orbitals with empty sigma star CH orbitals. In reality the favoured conformation has a gauche relationship. This is due to a stabilising interaction between vinyl protons and the pi orbitals. DOI:10.1021/ja00111a016 The conformer is displayed under Table 1 as Gauche 2. Figure 3 displays the HOMO and LUMO orbitals of 1,5 – hexadiene and the combined model. In the combined model we can see the stabilising overlap of orbitals. This interaction is why the gauche conformer is favoured. It can be seen in the model that there is overlapping of the same symmetry (red to red; green to green) and that the overlap is significant.

LUMO of Stable Gauche	HOMO of Stable Gauche	Combined: Overlapped Orbitals of Stable Gauche

Figure 3: Displays to show the stabilising interactions between the HOMO and LUMO of the Gauche Conformer

Comparison between HF and DFT methods: The Self Consistent Field Method (Hartree Fock) neglects the energy contribution from electrons of opposite spins but considers those of parallel spins. The solution of this method is found by iteration. From this exercise it can be seen that the Density Functional Theory gives a higher level of theory: a lower energy is obtained. The method takes into account electron energies in terms of probability density. It is better as it takes into account contributions from different energy sources. The overall geometry of the structure has a minimal change between methods. The symmetry labels remain the same.

Hartree Fock (A.U.)	-231.577110839
DFT (A.U.)	-231.69253528

Table 2: A comparison of energies using the Anti 2 conformer with DFT and HF level theories

A frequency calculation is carried out to check that the frequencies are real and to generate an infrared spectrum. If an imaginary frequency was obtained a transition structure would have been obtained: a saddle point. This was performed on the ANTI 2 structure under table 1: the resultant print screens are under figure 4. All vibrations are real.

Thermochemical property	Room Temperature	Temp = 0.1 , Pressure = 0.1
i. Sum of electronic and zero-point Energies	-234.428072	-234.428072
ii. Sum of electronic and thermal Energies (A.U.)	-234.420768	-234.428071
iii. Sum of electronic and thermal Enthalpies (A.U.)	-234.419823	-234.428070
iv. Sum of electronic and thermal Free Energies (A.U.)	-234.459698	-234.428071

Table 3: Summary of the thermochemical data obtained from a frequency calcualation

From table 3 we can see the obvious differences between calculating frequencies at different temperatures. The issue with this exercise was that when calculations were carried out at T=0 and P=0 it failed. To get over this issue calculations were carried out at T = 0.1 and P=0.1. You would expect the results for thermal chemistry calculations to be the same at 0K: the slight deviations are due to the calculations not being carried out at exactly zero.

Optimising Chair and Boat Transition Structures for COPE

An allyl fragment was made and optimised first. A guess for the chair transition structure was obtained by appending the two optimised fragments together. The two fragments are isoelectronic with the predicted diradical transition structure. The bond distances between the terminal ends of ally fragments were set to 2.2 angstroms. The fragments discussed above along with the optimised structure (Hartree Fock) are displayed under figure 5. The issue with this method is that the guess structure needs to be close to the actual structure.

Allyl Fragment	Guess TS Chair	Result

Figure 5: Optimising the Chair Transition Structure

An optimisation and frequency calculation was carried out: optimising to a TS (Berny). Opt=noEigen is an important key word to add to prevent the system from crashing from an inaccurate guess which leads to multiple imaginary frequencies being found. For this calculation an imaginary frequency was found at 817.15cm-1. The corresponding bond animation is displayed under figure 6. A frozen co-ordinate method was also used: this entailed freezing the bond distance between the two terminal ends of the reaction site.

The QST2 method works to find the transition structure between a specified reactant and product: it involves manually labelling reactants and products. For this method the initial guess needs to be close to the transition structure otherwise it fails. Figure 7 displays a labelled input molecule for the QST method and the transition structure the method obtains. The imaginary frequency obtained is 817.88cm-1: it is a transition structure.

The intrinsic reaction coordinate method or IRC is used to follow a Transition structure down to its local minimum. As the reaction is symmetrical a forward direction was computed only. It takes minimal steps down a reaction path (where the gradient is steepest) to find its local minimum. The number of steps taken therefore needs to be larger enough to find the local minimum. Figure 8 displays minima found when the calculation is set to 50 steps and a 100 steps: notice the 100 step calculation ends prematurely; it has found its transition structure.

50 Step Calculation	100 Step Calculation

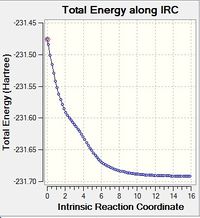
Figure 8: Graphs to show the IRC calculation finishing prematurely and going to completion to find the minima

Diels Alder

Diels Alder reactions are pericyclic. They occur when the pi orbitals of the dienophile are used to form a new sigma bonds with the pi orbitals of the diene: specifically when the HOMO of one reactant interacts with the LUMO of the other. The overlap needs to be of the same symmetry and have a large enough overlap density. The process is concerted or forbidden dependant on the number of pi electrons. DOI:10.1021/ed086p199

The Reaction under consideration is between ethylene and cis-butadiene. The HOMO and LUMO orbitals are listed under table 4, whilst the Transition Structure is displayed under figure 8. The transition structure had an imaginary vibrational frequency of -850.87cm-1 and energy of -232.80 A.U.

The Reaction is allowed as there is significant overlapping between orbitals of the same symmetry. The HOMO of ethylene interacts with the LUMO of cis-butadiene.

Compound, Orbitals Displayed	Structure and Orbitals	Symmetry
Ethylene, HOMO		Symmetric
Ethylene, LUMO		Anti-Symmetric
Cis-Butadiene, HOMO		Anti-Symmetric
Cis-Butadiene, LUMO		Symmetric
Cyclohexene TS, HOMO		Symmetric
Cyclohexene TS, LUMO		Symmetric

Table 4: HOMO and LUMO orbitals for Ethylene, Cis-Butadiene and Cyclohexene TS

The final reaction under consideration is between cyclohexa-1,3-diene and maleic anhydride. The product of this reaction has either an Exo or Endo geometry. The structures are listed under figure 9.

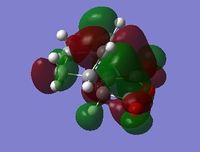
Listed under Table 5 are the energies and imaginary frequencies of the EXO and ENDO transition structures. Under Figure 10. are the ENDO and EXO products displayed with their HOMO and LUMO orbitals.

From table 5 we can see that the energies of the transition structures are quite similar. However the EXO TS has lower energy: this is probably due to a reduction in steric clashing. The ENDO products imaginary vibrational frequency is much lower than that of the EXO TS. The ENDO has a smaller reaction boundary to overcome and is the major product when the reaction is under kinetic control.

Geometry	Energy (A.U.)	Imaginary Frequency (cm-1)
Exo	-605.60359	-614.18
Endo	-605.58715	-428.97

Table 5: Summary of EXO and ENDO TS energies and imaginary frequencies

EXO TS with HOMO orbitals	EXO TS with LUMO orbitals	ENDO TS with HOMO orbitals	ENDO TS with LUMO orbitals

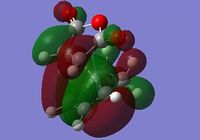
Figure 10: The EXO and LUMO TS with their corresponding HOMO and LUMO orbitals

References

1. DOI:10.1021/ed084p2001 2. DOI:10.1021/ja00101a078 3. DOI:10.1021/ja00111a016 4. DOI:10.1021/ed086p199