User:Nb1412

EX₃ section

Introduction

The EX₃ molecules that were analysed using computational chemistry are BH₃, BBr₃, GaBr₃ and NH₃. The program that were used was Gaussian to do optimisation, frequency, MO and NBO analysis of the EX₃ with exception of heavier molecule such as GaBr₃ where the analysis were done in High Performance Computing, HPC via online portal in order to minimise the CPU time.

Computational chemistry are useful in terms of the properties of the molecules like its transition state, the substituents effect, the IR and the vibrational frequencies of the molecule being analysed which will be shown later.¹

In the optimisation step, the minimum energy structures of the molecules are located on its potential energy surface or the moelcule transition structure.¹ The additional keyword used in the method step were 'integral=grid=ultrafine scf=conver=9'. The same keyword will he used for the frequency step. All the molecules used in this part are neutral thus in the method section of the optimisation step, the charge is set at zero with multiplicity of a singlet because 2S+1= 1. This step is very important in the project section as the ionic liquid molecules that were analysed as all positively charged. The gradient of the optimised molecule should be close to zero, for the stationary point on the potential energy surface is zero.¹ For the optimisation step, it is important to check whether the molecule we optimised has converged or not as shown later in the 'Optimisation summmary data' of the respective molecules. The details of the convergence criteria will not be discussed in this section. In the frequency step, we are confirming to have minimal structure deally, we would like all the frequency readings to be positive, but the program used is not perfect. Population analysis type that were used was the NBO population analysis.

In all the comparison that was done in this 'EX₃ section' and 'mini project section', whether its the optimisation, frequency, MO and NBO analysis were using the same method and basis set unless stated otherwise. Method/basis set used: B3LYP/3-21G level. The higher level of basis set that were used in some part of this report is 6-13G (d,p) and the medium basis set is LanL2DZ which was used for heavier group element of the periodic table.

Bond type and strengths

Table 1: Comparing bond strengths in terms of σ bonds of C atom

Bond type	Weak	Medium	Strong	info
C-H			✓	Bond length= 109 pm, bond energy= 411 kj/mol
C-C		✓		Bond length= 154 pm, bond energy= 346 kj/mol
C-Br	✓			Bond length= 194 pm, bond energy= 327 kj/mol

Table 2: Comparing bond strengths in terms of σ bonds of Si atom

Bond type	Weak	Medium	Strong	info
Si-H		✓		Bond length= 148 pm, bond energy= 318 kJ/mol
Si-O			✓	Bond length= 163 pm, bond energy= 452 kJ/mol
Si-I	✓			Bond length= 243 pm, bond energy= 234 kJ/mol

In general, the shorter the bond the more s-character thus more energy is needed to break the bond. As shown in the above table, Si-O is a much stronger bond in comparison to all the above bonds. This shows that the definition of bond strength is different for every atom, it is not a fixed property but rather a spectrum. Its the same as the ligand spectrochemical series are slightly different or very different for every metal complex. Data in table 1 and 2 was taken from reference ^[[2]]

So what is bond? Bond can not be seen physically, so how do we define it? The best way to explain what a bond is by referring to the probability at which we find the most electrons to be in. ^[[3]]

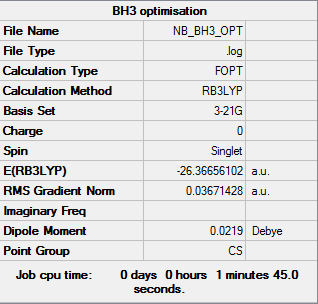
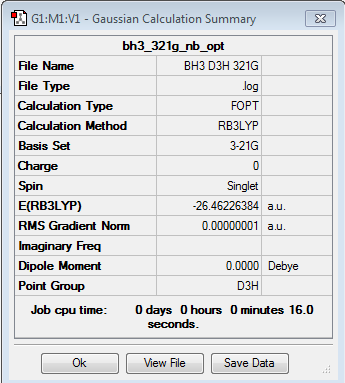
BH₃

Optimisation of BH₃: B3LYP/3-21G level with Cs symmetry

Optimisation log file here

Table 3: Optimisation data summary

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000220 0.000450 YES RMS Force 0.000106 0.000300 YES Maximum Displacement 0.000940 0.001800 YES RMS Displacement 0.000447 0.001200 YES	Optimised Borane Molecule

This molecule, BH₃ should have a D3h symmetry, but since we set the bond lengths of B-H bond to 1.53 angstrom, one B-H bond to 1.54 angstrom, and the third B-H bond to 1.55 angstrom, before we optimised them, we break the D3h symmetry to Cs point group.

Optimisation of BH₃: B3LYP/3-21G level with D3h symmetry

Optimisation log file here

Table 4: Optimisation data summary

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000000 0.000015 YES RMS Force 0.000000 0.000010 YES Maximum Displacement 0.000000 0.000060 YES RMS Displacement 0.000000 0.000040 YES	Optimised Borane Molecule, D3h symmetry

With basis set of 3-21g, the bond length of B-H is 1.19(4) Å while the bond angle is 120 °.

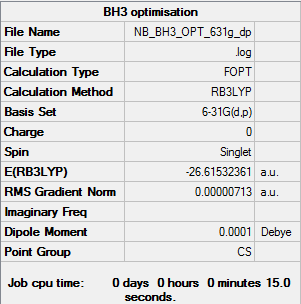
Optimisation of BH₃: B3LYP/6-31G(d,p) level with Cs symmetry

Optimisation log file here

Table 5: Optimisation data summary

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000012 0.000450 YES RMS Force 0.000008 0.000300 YES Maximum Displacement 0.000063 0.001800 YES RMS Displacement 0.000039 0.001200 YES	Optimised Borane Molecule

Optimisation of BH₃: B3LYP/6-31G(d,p) level with D3h symmetry

Optimisation log file here

Table 6: Optimisation data summary

summary data	convergence	Jmol
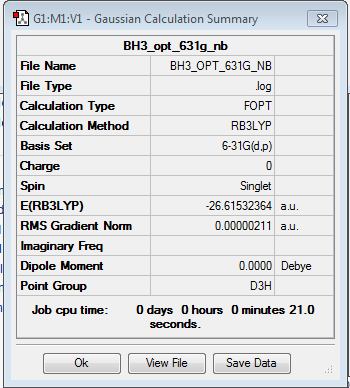
	Item Value Threshold Converged? Maximum Force 0.000004 0.000015 YES RMS Force 0.000003 0.000010 YES Maximum Displacement 0.000017 0.000060 YES RMS Displacement 0.000011 0.000040 YES	Optimised Borane Molecule, D3h symmetry

With D3h symmetry point group, the bond angle between H-B-H is 120^° while the bond length of B-H is 1.19(2) Å. The bond length for B-H is shorter when we use a higher basis set (6-21g) when compared with using 3-21g basis set, which indicates the accuracy of the bond length when using a higher basis set where the experimental value of B-H bond length is 1.19 Å. [[4]]

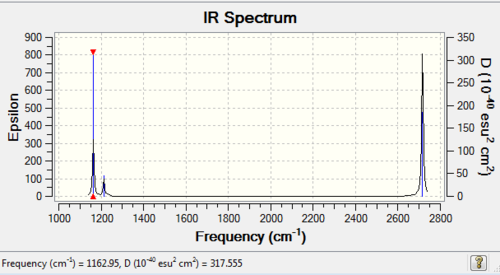
Frequency Analysis of BH₃ :B3LYP/6-31G(d,p) level

D-space of BH₃ frequency file Link DOI:10042/147675

Frequency file: here

Table 7: Frequency data summary

summary data	low modes
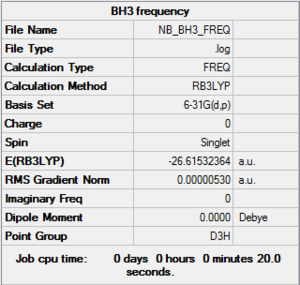
	Low frequencies --- -14.5190 -14.5149 -10.8207 0.0006 0.0169 0.3454 Low frequencies --- 1162.9508 1213.1230 1213.1232

Vibrational Analysis for BH₃

Table 8: Vibrational data summary

wavenumber	Intensity	IR active?	type
1163	93	yes	bend (wagging i.e. umbrella motion)
1213	14	very slight	bend (rocking)
1213	14	very slight	bend (scissoring)
2583	0	no	symmetrical stretch
2716	126	yes	asymmetric stretch
2716	126	yes	asymmetric stretch

Diagram 1:IR spectrum of BH₃

|

BH₃ is a polyatomic molecule thus to calculate the number of vibration is 3N-6 where N is the number of atoms of the molecule. The '-6' factor is due to the redundant translational and rotational motion of the molecules which does not contribute to the property of the molecule.[[5]]

Comparison of real MOs and LCAO MOs diagrams of BH₃ molecule

Table 9: BH₃ molecule

MO diagram of BH3 molecule

Table 10: BH₃ molecule

More Info
	Real MO	LCAO MO	Comments
1a'		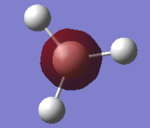	The LCAO MO is simple and basically saying that this is a core AO which exhibit s-orbital, it being the lowest occupied AO. What it does not tell us, is the H atoms contributions to the MO. As shown under the 'Real MO', 1a' MO, the H AO does not contribute at all to the 1a' MO, meaning the electron density is localised at the centre of the molecule, the B atom only. Therefore, while it is easy assume that it is the core MO, it is not exactly accurate in terms of explaining which AO contribute to the orbital.
2a'		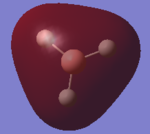	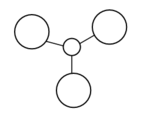The LCAO MO shows the s-atomic orbital of the atoms are in phase and overlap with each other. The LCAO shows the H AO contributes more to the bonding properties of the MO but when we looked at the 'real MO' of 2a', the electron density of the MO is evenly delocalised throughout all the atoms. The LCAO is accurate in terms of the s-orbitals of the B and H atoms contribute to the bonding MO.
1e'		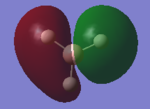	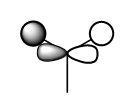In the 'real MO', there is an internuclear node at the B atom and this is depicted accurately in the LCAO MO, as the MO is more anti-bonding due to the p-orbital of B contribution.
1e'			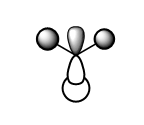In the 'real MO', there is an internuclear node at the B atom and this is depicted accurately in the LCAO MO, as the MO is more anti bonding due to the p-orbital of B contribution. The degeneracy is not obvious from LCAO when in comparison to 'real MO', where the colour of the MO is the only thing that is different but the size of the of contribution does not change in 'real MO', this is not obvious from the 'LCAO'.
1a2		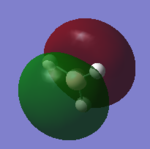	The 'real MO' shows an internuclear node at the B atom, and this was showed accurately by the LCAO where the antibonding contribution comes from B atom. What is not clear is that the internuclear nodes at the H atoms in 'real MO' is not depicted clearly in LCAO.
3a1'			There are 3 nodal planes perpendicular to the B-H bond and this shows in the 'real MO' clearly which contributes to the high antibonding and thus high in energy for the MO. The 'real MO' shows that the s-orbital of the B atom smeared across the different phase of the s-orbital of the H atom and this is not shown in the LCAO. Thus LCAO does not show the effect of the opposite phase have on each other.
2e'			There are internuclear node at the B atom and 2 nodal plane perpendicular across the B-H bond. The LCAO shows the p-orbital contribution of B to the antibonding nature of the MO and thus the high energy in comparison to the MO before this. The s-orbital of the opposite phase of the H was not shown to be smeared in the LCAO.
2e'		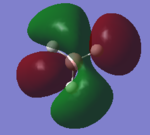	There are internuclear node at the B atom and 2 nodal plane perpendicular across the B-H bond. The LCAO shows the p-orbital contribution of B to the antibonding nature of the MO and thus the high energy in comparison to the MO before this. The s-orbital of the opposite phase of the H was not shown to be smeared in the LCAO.

BBr₃

Optimisation of BH₃: GEN level

D-Space Link of optimisation file DOI:10042/143692

Optimisation log file here

Table 11:

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000015 0.000450 YES RMS Force 0.000008 0.000300 YES Maximum Displacement 0.000100 0.001800 YES RMS Displacement 0.000058 0.001200 YES	Optimised Boron tribromide Molecule

This molecule, BBr₃ should have D3h symmetry i.e trigonal planar.

GaBr₃

Optimisation of GaBr₃: B3LYP/LANL2DZ level

Optimisation log file here

Table 12:

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000003 0.001800 YES RMS Displacement 0.000002 0.001200 YES	Optimised Gallium(III) bromide Molecule

Optimisation of GaBr₃: B3LYP/ 6-31G(d,p)level

Optimisation log file here

Table 13

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000072 0.000450 YES RMS Force 0.000047 0.000300 YES Maximum Displacement 0.000434 0.001800 YES RMS Displacement 0.000284 0.001200 YES	Optimised Gallium(III) bromide Molecule

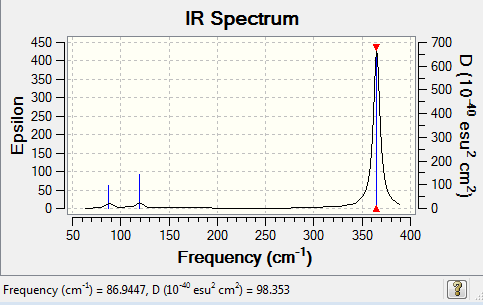
Frequency Analysis of GaBr₃:B3LYP/6-31G(d,p) level

Frequency log file: here

Table 14:

summary data	low modes
	Low frequencies --- -3.3718 -3.3718 -2.7645 -0.0135 -0.0115 0.0139 Low frequencies --- 86.9447 86.9448 119.6983

Vibrational Analysis for GaBr₃:B3LYP/6-31G(d,p)

Table 15:

wavenumber	Intensity	IR active?	type
87	2	very slight	bend (rocking)
87	2	very slight	bend (scissoring)
120	4	very slight	bend (wagging i.e. umbrella motion)
235	0	no	symmetrical stretch
365	62	yes	asymmetrical stretch
365	62	yes	asymmetrical stretch

Diagram 2:IR spectrum of GaBr₃

|

NH₃

The point group of NH₃ miolecule is C_3v as 3σ_v and 2C₃.

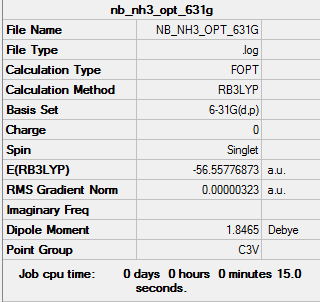
Optimisation Analysis of NH₃: B3LYP/6-31G(d,p) level

Optimisation log file here

Table 16:

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000006 0.000015 YES RMS Force 0.000004 0.000010 YES Maximum Displacement 0.000011 0.000060 YES RMS Displacement 0.000008 0.000040 YES	Optimised Ammonia Molecule

NBO Analysis of NH₃: B3LYP/6-31G(d,p) level

Table 17:

Population Analysis	Summary of Natural Population Analysis
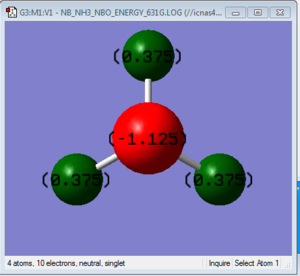		Summary of Natural Population Analysis: Natural Atom No Charge ---------------------- N 1 -1.12514 H 2 0.37505 H 3 0.37505 H 4 0.37505 ======================= * Total * 0.00000

The charge distribution shows that N atom in NH₃ is the only electronegative atom in the molecule and since the total charge of the molecule is zero, the remaining positive charge is distributed evenly to the H atoms. This is not a formal charge but relative to the atoms in the molecule itself.

Table 18:

Bond orbital/ coefficients/ hybrids

(Occupancy) Bond orbital/ Coefficients/ Hybrids --------------------------------------------------------------------------------- 1. (1.99909) BD ( 1) N 1 - H 2 ( 68.83%) 0.8297* N 1 s( 24.86%)p 3.02( 75.05%)d 0.00( 0.09%) ( 31.17%) 0.5583* H 2 s( 99.91%)p 0.00( 0.09%) 2. (1.99909) BD ( 1) N 1 - H 3 ( 68.83%) 0.8297* N 1 s( 24.86%)p 3.02( 75.05%)d 0.00( 0.09%) ( 31.17%) 0.5583* H 3 s( 99.91%)p 0.00( 0.09%) 3. (1.99909) BD ( 1) N 1 - H 4 ( 68.83%) 0.8297* N 1 s( 24.86%)p 3.02( 75.05%)d 0.00( 0.09%) ( 31.17%) 0.5583* H 4 s( 99.91%)p 0.00( 0.09%) 4. (1.99982) CR ( 1) N 1 s(100.00%) 5. (1.99721) LP ( 1) N 1 s( 25.38%)p 2.94( 74.52%)d 0.00( 0.10%)

The table above shows that the hybridisation of the atoms in the NH₃ and also the contribution of each atom to the bond. For the N-H, N atom contributes 69% to the N-H bond.

Table 19:

Natural Bond Orbital Summary
Natural Bond Orbitals (Summary): Principal Delocalizations NBO Occupancy Energy (geminal,vicinal,remote) ==================================================================================== Molecular unit 1 (H3N) 1. BD ( 1) N 1 - H 2 1.99909 -0.60417 2. BD ( 1) N 1 - H 3 1.99909 -0.60417 3. BD ( 1) N 1 - H 4 1.99909 -0.60417 4. CR ( 1) N 1 1.99982 -14.16768 5. LP ( 1) N 1 1.99721 -0.31757

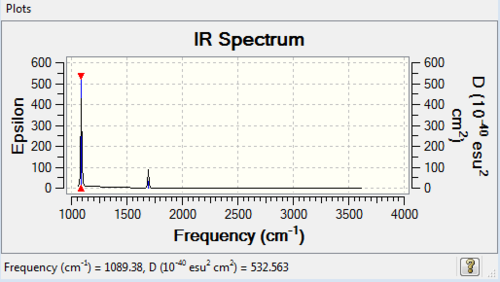
Vibrational spectrum for NH₃

Table 20:

wavenumber	Intensity	IR active?	type
1089	145	yes	bend
1694	14	very slight	bend
1694	14	very slight	bend
3461	1	no	stretch
3591	0	no	stretch
3591	0	no	stretch

Diagram 3: IR Spectrum of NH₃

MO analysis of NH₃: B3LYP/6-31G(d,p) level with C_3v symmetry

MO analysis of NH₃ log file here

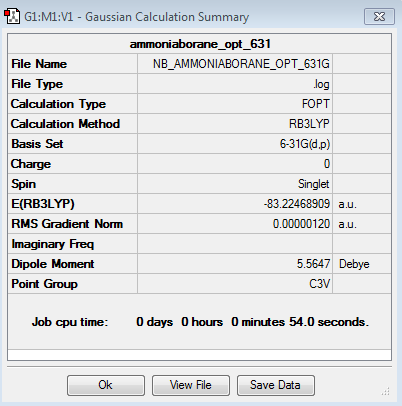
NH₃BH₃: B3LYP/6-31G(d,p) level with C_3v symmetry

Optimisation of NH₃BH₃: B3LYP/6-31G(d,p) level with C_3v symmetry

Optimisation log file here

Table 21: Optimisation data summary

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000002 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000023 0.000060 YES RMS Displacement 0.000010 0.000040 YES	Optimised Ammonia Borane

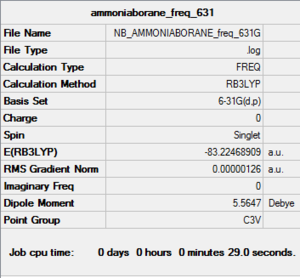
Frequency Analysis of NH₃BH₃: B3LYP/6-31G(d,p) level with C_3v symmetry

Frequency log file: here

Table 22:

summary data	low modes
	Low frequencies --- -5.5864 -0.3039 -0.0444 0.0009 1.2177 1.2912 Low frequencies --- 263.2843 632.9623 638.4603

Vibrational spectrum for NH₃BH₃

Table 23:

wavenumber	Intensity	IR active?	type
263	0	no	bend
633	14	very slight	stretch
638	4	very slight	bend
638	4	very slight	bend
1069	41	yes	bend
1069	41	yes	bend
1196	109	yes	bend
1204	3	yes	bend
1204	3	yes	bend
1329	114	yes	bend
1676	28	very slight	bend
1676	28	very slight	bend
2472	67	yes	stretch (symmetric)
2532	231	yes	stretch (anti-symmetric)
2532	231	yes	stretch (anti-symmetric)
3464	3	very slight	stretch (symmetric)
3581	28	yes	stretch (anti-symmetric)
3581	28	very slight	stretch (anti-symmetric)

Determination of the dative bond energy

Table 24: Dissociation Energy calculation

	Energy values
E(NH3)	-148490 kJ/mol
E(BH3)	-69880 kJ/mol
E(NH3BH3)	-218510 kJ/mol
[E(NH3BH3)]- [E(NH3) + E(BH3)]	-140 kJ/mol

BH₃ molecule have an empty p-orbital on the B atom which makes it Lewis acid i.e. electron acceptor as it is electron deficient molecule. Therefore BH₃ in reality does not exist on its own, it prefers to exist in dimer, usually with itself, thus forming BH₃BH₃ adduct. Based on the dissociation energy of NH₃BH₃ is lower compared to the constituents energy of NH₃ and BH₃ from the calcualtion, this indicates that the molecule prefers to be in NH₃BH₃ rather than in the constituents NH₃ and BH₃ as it provides stabilisation in adduct from.

Diagram 4:IR Spectrum of NH₃BH₃

Mini Project section

In this mini project, ionic liquid properties were analysed computationally suing Gaussian. In order to obtain a valid result when comparing the ionic liquids, the same method and basis set were used i.e B3LYP/6-31G(d,p) level. The point group of the ionic liquid are summarised bellow. It was noticed that there is a limitation with the Gaussian is that they analysed the molecule as it is drawn which is the case for [N(CH₃)₃CH₂OH]⁺ where the torsion angle of the moelcule drawn had to be changed manually.

Comparison of selected 'onium' cations

Table 25: Geometry Data

	[N(CH3)4]+	[P(CH3)4]+	[S(CH3)3]+
r(E-Me)	1.51 Å	1.82 Å	1.82 Å
r(C-H)	1.09 Å	1.09 Å	1.09 Å
θ(Me-E-Me)	109.5 °	109.5 °	102.7 °
θ(H-C-H)	110.0 °	109.0 °	109.4 °
Point Group	Td	Td	C3v

[N(CH₃)₄]⁺

Optimisation Analysis of [N(CH₃)₄]⁺:B3LYP/6-31G level with Td symmetry

D-space of [N(CH₃)₄]⁺ optimisation file Link DOI:10042/157429

Table 26: Summary of the [N(CH₃)₄]⁺ optimisation data

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000003 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000013 0.000060 YES RMS Displacement 0.000005 0.000040 YES	Optimised molecule

Frequency Analysis

D-space of [N(CH₃)₄]⁺ frequency file Link DOI:10042/157433

Table 27 :Summary of [N(CH₃)₄]⁺ frequency data

summary data	low modes
	Low frequencies --- -0.0004 -0.0004 0.0003 21.5288 21.5288 21.5288 Low frequencies --- 188.5489 292.6546 292.6546

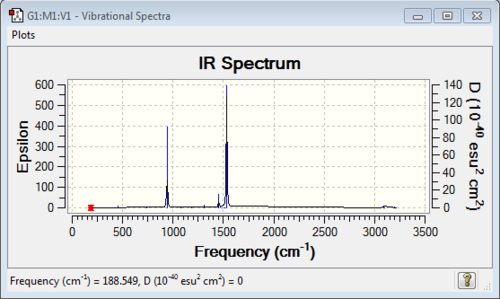
Vibrational Analysis for [N(CH₃)₄]⁺:

Table 28 : Summary of [N(CH₃)₄]⁺ Vibrational data

wavenumber	Intensity	IR active?	type
189	0	no	bend
293	0	no	bend
293	0	no	bend
293	0	no	bend
362	0	no	bend
362	0	no	bend
456	0	no	bend
456	0	no	bend
456	0	no	bend
736	0	no	symmetric stretch
941	22	yes (very slight)	asymmetric stretch and bend
941	22	yes (very slight)	asymmetric stretch and bend
941	22	yes (very slight)	asymmetric stretch and bend
1078	0	no	bend
1078	0	no	bend
1078	0	no	bend
1185	0	no	bend
1185	0	no	bend
1306	11	yes (very slight)	bend
1306	11	yes (very slight)	bend
1306	11	yes (very slight)	bend
1456	5	yes (very slight)	bend
1456	5	yes (very slight)	bend
1456	5	yes (very slight)	bend
1487	0	no	bend
1487	0	no	bend
1487	0	no	bend
1502	0	no	bend
1502	0	no	bend
1512	0	no	bend
1532	54	yes	bend
1532	54	yes	bend
1532	54	yes	bend
3087	1	yes (very slight)	stretch (anti-symmetric)
3087	1	yes (very slight)	stretch (anti-symmetric)
3096	0	no	symmetrical stretch
3189	0	no	symmetrical stretch
3189	0	no	symmetrical stretch
3189	0	no	symmetrical stretch
3190	0	no	symmetrical stretch
3195	1	yes (very very slight)	symmetrical stretch
3195	1	yes (very very slight)	symmetrical stretch
3195	1	yes (very very slight)	symmetrical stretch

Diagram 5:IR spectrum of [N(CH₃)₄]⁺

|

MO Analysis

D-space of [N(CH₃)₄]⁺ MO analysis file Link DOI:10042/157836

Table 29: Summary of [N(CH₃)₄]⁺ MO analysis

	Real MO	Comments
Bonding		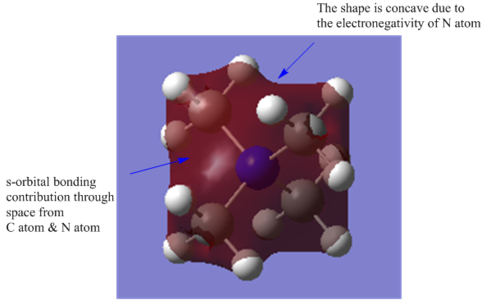This is the highly bonding MO, where the s-orbital of N atom and C atoms contribute to the bonding of the MO, through space interactions. The MO are very delocalised across all the atoms. There is no nodes at all in this MO.
Bonding		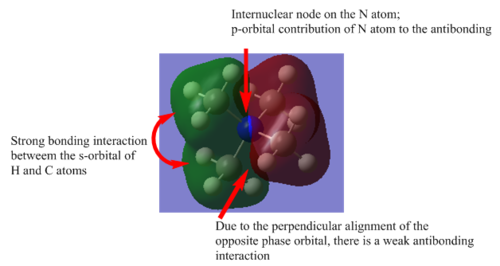The existance of the node increases the energy of the bonding MO, together with the perpendicular alignment of the opposite phase. There are bonding through space interactions between the C and the H atoms on the methyl groups. There is no nodal plane. The MO is delocalised with respect to the 2 methyl groups.
Bonding		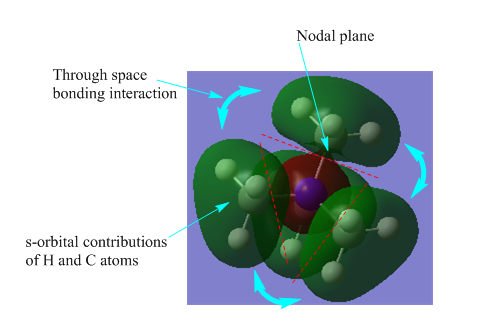There are 3 nodal planes perpendicular through the N-C bonds and this contributes to the high energy thus the antibonding part. For the 4 methyl groups on the N atom, their s-orbital overlap and contributes to the bonding of the MO. The MO is not very delocalised as shown in the diagram, where the s-orbital of the N atom localised to itself.
Bonding		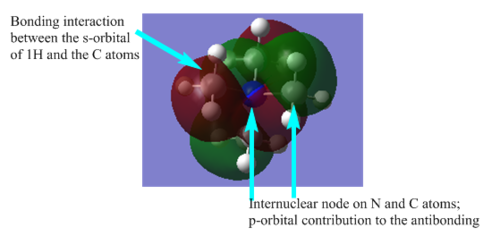There are 5 nodes in the MO which contributes to the antibonding and high energy of the MO. The MO is mostly localised on the individual methyl group and the N atom.
Bonding		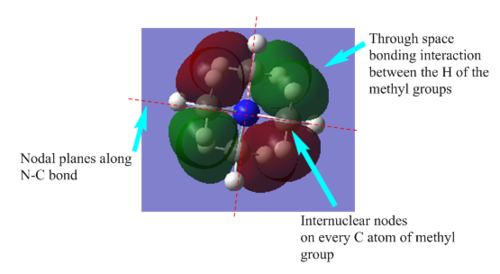The existance of the 4 nodal planes along the C-N bonds and the 4 internuclear nodes on the C atoms of the methyl group contributes to the antibonding nature of the MO thus the high energy. There is partial through space bonding interactions of the s-orbitals of the H atoms of the methyl group.

It is noted that only one of the degenerate orbitals of each energy level were analysed due to it redundancy.

NBO Analysis of [N(CH₃)₄]⁺

Table 30 : Summary of [N(CH₃)₄]⁺ Population Analysis

Population Analysis	Summary of Natural Population Analysis
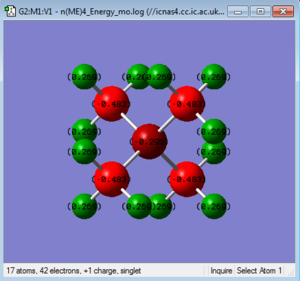		Summary of Natural Population Analysis: Natural Atom No Charge ----------------------- N 1 -0.29516 C 2 -0.48342 H 3 0.26907 H 4 0.26907 H 5 0.26907 C 6 -0.48342 H 7 0.26907 H 8 0.26907 H 9 0.26907 C 10 -0.48342 H 11 0.26907 H 12 0.26907 H 13 0.26907 C 14 -0.48342 H 15 0.26907 H 16 0.26907 H 17 0.26907 ======================= * Total * 1.00000

Looking at the summary of the population analysis, the total charge of the molecule i.e. +1 are divided for the atoms, with carbon being the most negative charge, then nitrogen and the positively charged hydrogen. It is an arbitrary assignment of charges, not electron density.

[P(CH₃)₄]⁺

B3LYP/6-31G(d,p) level

D-space of [P(CH₃)₄]⁺ optimisation file Link DOI:10042/158471

Table 31 : Summary of [P(CH₃)₄]⁺ optimisation data

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000001 0.000015 YES RMS Force 0.000000 0.000010 YES Maximum Displacement 0.000005 0.000060 YES RMS Displacement 0.000002 0.000040 YES	Optimised molecule

D-space of [P(CH₃)₄]⁺ frequency file Link DOI:10042/158506

Table 32:Summary of [P(CH₃)₄]⁺ frequency data

summary data	low modes
	Low frequencies --- -0.0017 -0.0011 0.0025 24.7242 24.7243 24.7243 Low frequencies --- 160.0696 194.8034 194.8034

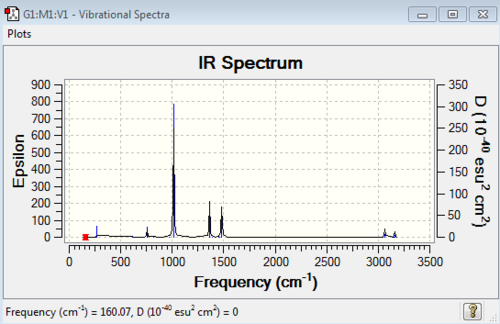
Diagram 6: IR Spectrum of [P(CH₃)₄]⁺

Vibrational spectrum for [P(CH₃)₄]⁺

Table 33:

wavenumber	Intensity	IR active?	type
160	0	no	bend
195	0	no	bend
195	0	no	bend
195	0	no	bend
223	0	no	bend
223	0	no	bend
271	2	yes (very very slight)	bend
271	2	yes (very very slight)	bend
271	2	yes (very very slight)	bend
615	0	no	symmetrical stretch
756	4	yes (very very slight)	bend
756	4	yes (very very slight)	bend
756	4	yes (very very slight)	bend
824	0	no	bend
824	0	no	bend
824	0	no	bend
973	0	no	bend
973	0	no	bend
1013	78	yes	bend
1013	78	yes	bend
1013	78	yes	bend
1362	21	yes	bend
1362	21	yes	bend
1362	21	yes	bend
1389	0	no	bend
1454	0	no	bend
1454	0	no	bend
1454	0	no	bend
1462	0	no	bend
1462	0	no	bend
1481	26	yes	bend
1481	26	yes	bend
1481	26	yes	bend
3064	5	yes (very very slight)	asymmetric stretch
3064	5	yes (very very slight)	asymmetric stretch
3064	5	yes (very very slight)	asymmetric stretch
3066	0	no	symmetric stretch
3157	0	no	symmetric stretch
3157	0	no	symmetric stretch
3158	0	no	symmetric stretch
3158	0	no	symmetric stretch
3160	4	yes	symmetric stretch
3160	4	yes	symmetric stretch
3160	4	yes	symmetric stretch

MO Analysis

D-space of [P(CH₃)₄]⁺ MO analysis file Link DOI:10042/160143

NBO Analysis of [P(CH₃)₄]⁺

Table 34 : Summary of [P(CH₃)₄]⁺ Population Analysis

Population Analysis	Summary of Natural Population Analysis
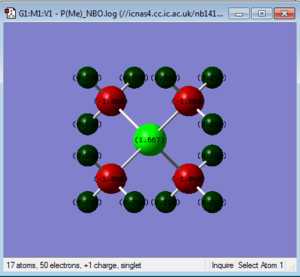		Summary of Natural Population Analysis: Natural Atom No Charge ----------------------- P 1 1.66680 C 2 -1.06021 H 3 0.29784 H 4 0.29784 H 5 0.29784 C 6 -1.06021 H 7 0.29784 H 9 0.29784 C 10 -1.06021 H 11 0.29784 H 12 0.29784 H 13 0.29784 C 14 -1.06021 H 15 0.29784 H 16 0.29784 H 17 0.29784 ======================= * Total * 1.00000

[S(CH₃)₃]⁺

B3LYP/6-31G level

D-space of [S(CH₃)₃]⁺ optimisation file Link DOI:10042/160621

Table 35:

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000002 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000054 0.000060 YES RMS Displacement 0.000017 0.000040 YES	Optimised [N(CH)]

D-space of [S(CH₃)₃]⁺ frequency file Link DOI:10042/160634

Table 36:

summary data	low modes
	Low frequencies --- -8.1009 -7.7505 -7.7472 -0.0025 0.0018 0.0090 Low frequencies --- 161.9980 199.6776 199.6776

Vibrational spectrum for [S(CH₃)₃]⁺

Table 37:

wavenumber	Intensity	IR active?	type
162	0	no	bend
200	0	no	bend
200	0	no	bend
255	0	no	bend
255	0	no	bend
285	0	no	bend
624	2	yes (very very slight)	symmetrical stretch
704	1	yes (very very slight)	asymmetrical stretch
704	1	yes (very very slight)	asymmetrical stretch
918	0	no	bend
958	1	yes (very very slight)	bend
958	1	yes (very very slight)	bend
1071	11	yes	bend
1071	11	yes	bend
1076	12	yes	bend
1371	0	no	bend (umbrella motion of 2 methyl group)
1371	0	no	bend (umbrella motion of 2 methyl group)
1408	2	yes (very very slight)	bend (umbrella motion of all methyl group)
1452	0	no	bend (scissoring)
1464	10	yes	bend (scissoring of Me groups)
1464	10	yes	bend (scissoring of Me groups)
1473	25	yes	bend (scissoring of Me groups)
1473	25	yes	bend (scissoring of Me groups)
1485	42	yes	bend (scissoring of Me groups)
3074	0	no	symmetrical stretch
3075	3	yes (very very slight)	asymmetrical stretch
3075	3	yes (very very slight)	asymmetrical stretch
3184	0	no	symmetrical stretch
3185	8	yes	symmetrical stretch
3185	8	yes	symmetrical stretch
3187	3	yes (very very slight)	symmetrical stretch
3187	2	yes (very very slight)	asymmetrical stretch
3187	2	yes (very very slight)	asymmetrical stretch

NBO Analysis of [S(CH₃)₃]⁺

Table 38 : Summary of [S(CH₃)₃]⁺ Population Analysis

Population Analysis	Summary of Natural Population Analysis
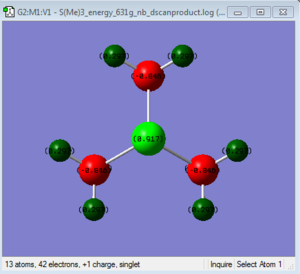		Summary of Natural Population Analysis: Natural Atom No Charge ----------------------- P 1 1.66680 C 2 -1.06021 H 3 0.29784 H 4 0.29784 H 5 0.29784 C 6 -1.06021 H 7 0.29784 H 8 0.29784 H 9 0.29784 C 10 -1.06021 H 11 0.29784 H 12 0.29784 H 13 0.29784 C 14 -1.06021 H 15 0.29784 H 16 0.29784 H 17 0.29784 ======================= * Total * 1.00000

Comparing the different ionic liquids

NBO analysis was used to compare and contrast the charge distribution across the ionic liquids with different cations i.e. Nitrogen, Phosphoros and Sulfur.

Table 39 : Summary of NBO population analysis

	X contribution to C-X	X hybridisation	C contribution to C-X	C hybridisation
N	66%	25%s+75%p i.e. sp3	34%	21%s+79%p i.e sp3
P	40%	25%s+74%p+1%d i.e. sp2d	60%	25%s+75%p i.e. sp3
S	51%	17%s+82%p+1%d	49 %	20%s+80%p i.e i.e. sp4

The electronegativity N=3.0, S=2.5 and P=2.1 and this gives different contribution to the C-X bond as shown.

Table : Comparing the charge distribution of the ionic liquids

	[N(CH3)4]+	[P(CH3)4]+	[S(CH3)3]+
Specific NBO charges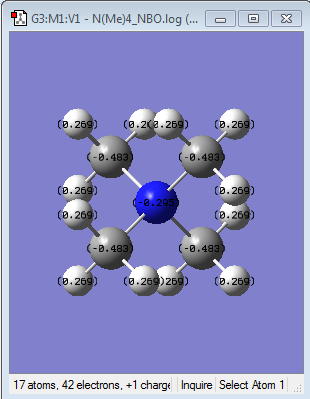
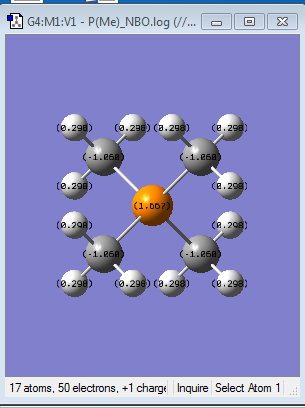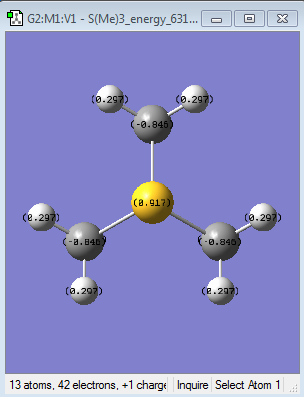
Colour atom by charge
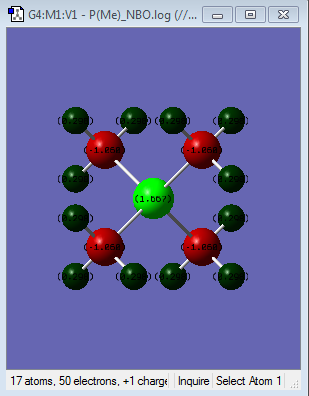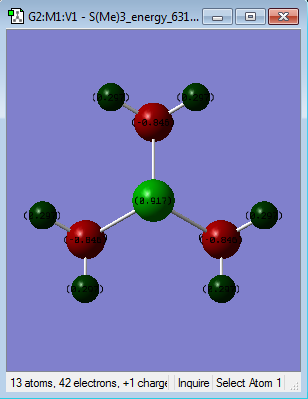
NBO Charge Distribution

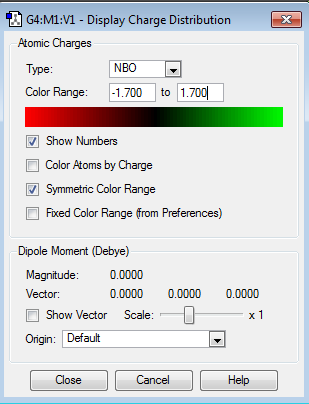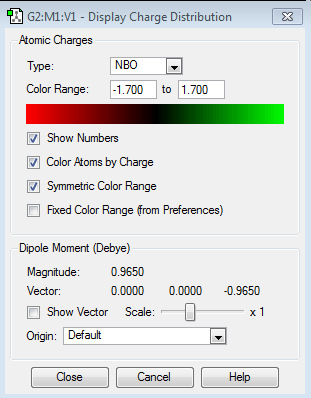
Influence of Functional Group

In this section, the effect of functional groups replacing one of the methyl group on the N(Me) were analysed. Hydroxyl and nitrile fucntional group were used. OH is an electron donating group and CN is the electron withdrawing group.By doing this, two different effect can be compared with the control i.e. [N(CH₃)₄]⁺. By carrying out MO and NBO analysis on [N(Me)₃(FG)]⁺ where FG is the respective functional group, the charge distribution and their effect on the HUMO and LUMO of the three compounds i.e. [N(CH₃)₄]⁺, [N(CH₃)₃(CH₂OH)]⁺ and [N(CH₃)₃(CH₂CN)]⁺ can be analysed.

[N(CH₃)₃(CH₂OH)]⁺

Optimisation of [N(CH₃)₃(CH₂OH)]⁺: B3LYP/6-31G(d,p) level

Charge= 1, Spin: singlet

D-space of [N(CH₃)₃(CH₂OH)]⁺:B3LYP/6-31G level optimisation file Link DOI:10042/161009

Table 40 : Summary of [N(CH₃)₃(CH₂OH)]⁺:B3LYP/6-31G level optimisation data

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000002 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000054 0.000060 YES RMS Displacement 0.000017 0.000040 YES	Optimised [N(CH)(CHOH)]

Frequency analysis of [N(CH₃)₃(CH₂OH)]⁺: B3LYP/6-31G(d,p) level

D-space of [N(CH₃)₃(CH₂OH)]⁺:B3LYP/6-31G level frequency file Link DOI:10042/161011

Table 41: Summary of [N(CH₃)₃(CH₂OH)]⁺:B3LYP/6-31G level frequency data

summary data	low modes
	Low frequencies --- -118.5298 -7.0356 -6.6962 -4.9877 0.0006 0.0009 Low frequencies --- 0.0012 129.5539 217.2942

Using a 'high' 6-31G(d,p) level basis set does not gave a good result as shown in the above table. The 'low frequency' values are too largely negative, -118.529 as shown above. Thus, using a 'medium' basis set, LanL2DZ but maintain the same method of B3LYP, we got an approximately good 'low frequency' in comparison to the higher basis set, 6-31G (d,p) level.

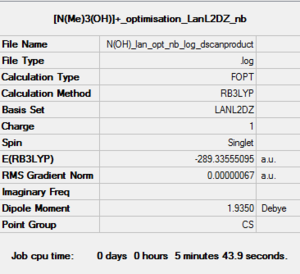
Optimisation of [N(CH₃)₃(CH₂OH)]⁺: B3LYP/LanL2DZ level

Charge= 1, Spin: singlet

D-space of [N(CH₃)₃(CH₂OH)]⁺:B3LYP/LanL2DZ level optimisation file Link DOI:10042/161016

Table 42 : Summary of [N(CH₃)₃(CH₂OH)]⁺:B3LYP/LanL2DZ level optimisation data

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000002 0.000015 YES RMS Force 0.000000 0.000010 YES Maximum Displacement 0.000008 0.000060 YES RMS Displacement 0.000003 0.000040 YES	Optimised molecule

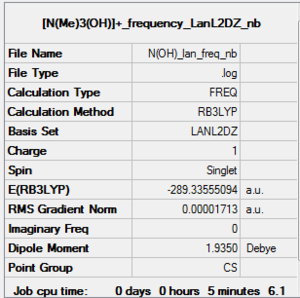
Frequency analysis of [N(CH₃)₃(CH₂OH)]⁺: B3LYP/LanL2DZ level

D-space of [N(CH₃)₃(CH₂OH)]⁺:B3LYP/LanL2DZ level frequency file Link DOI:10042/161017

Table 43 : Summary of [N(CH₃)₃(CH₂OH)]⁺:B3LYP/LanL2DZ level frequency data

summary data	low modes
	Low frequencies --- -8.4520 -7.3510 -5.5751 -0.0009 -0.0001 0.0009 Low frequencies --- 90.9596 107.4403 191.6445

As noted before using medium basis set, LanL2DZ for [N(CH₃)₃(CH₂OH)]⁺ gave a good low frequency but it is not accurate. LanL2DZ i.e Pseudo-potential should only be used on heavy atoms, row threee Therefore the result that were obtained using LanL2DZ will not be used.

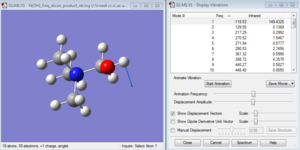
After doing the animated vibration of [N(CH₃)₃(CH₂OH)]⁺:B3LYP/6-31g with Cs point group symmetry, it shows that the O-H group was doing the bending motion in one plane only as shown in the diagram as evident with the 'displacement vector'.

[N(CH₃)₃(CH₂OH)]⁺:B3LYP/6-31g with Cs point group.

With Gaussian, drawing the molecule can mislead us to having different point group. In [N(CH₃)₃(CH₂OH)]⁺ case, we have to manually change the torsion angle between H-C-O as shown in the diagram as (1), (2) and (3) respectively. We do this to make the OH group to have more rotational freedom.

[N(CH₃)₃(CH₂OH)]⁺:B3LYP/6-31g with C1 point group.

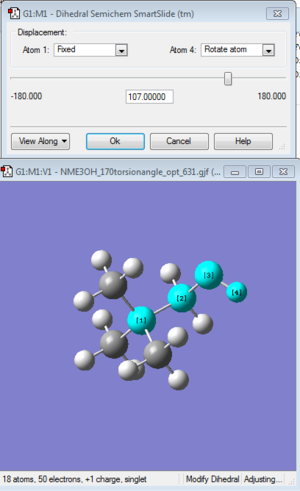
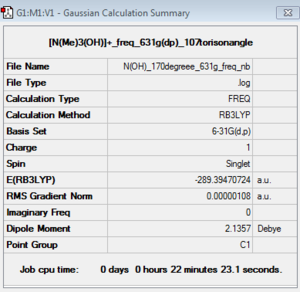
Optimisation of [N(CH₃)₃(CH₂OH)]⁺: B3LYP/6-31G(d,P) level with torsion angle of 107^°

Charge= 1, Spin: singlet with torsion angle between C-N and C-O as 107^°.

D-space of [N(CH₃)₃(CH₂OH)]⁺:B3LYP/6-31G(d,P) level optimisation file Link DOI:10042/155637

Table 44 : Summary of [N(CH₃)₃(CH₂OH)]⁺:B3LYP/6-31G(d,P) level optimisation data

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000002 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000053 0.000060 YES RMS Displacement 0.000013 0.000040 YES	Optimised molecule

Frequency analysis of [N(CH₃)₃(CH₂OH)]⁺: B3LYP/6-31G(d,P) level with torsion angle of 107^°

D-space of [N(CH₃)₃(CH₂OH)]⁺:B3LYP/6-31G(d,P) level frequency file Link DOI:10042/161032

Table 45 : Summary of [N(CH₃)₃(CH₂OH)]⁺:B3LYP/6-31G(d,P) level frequency data

summary data	low modes
	Low frequencies --- -8.5281 -5.1364 -1.6469 -0.0015 -0.0013 -0.0013 Low frequencies --- 131.0879 213.4335 255.7052

MO analysis of [N(CH₃)₃(CH₂OH)]⁺: B3LYP/6-31G(d,P) level with torsion angle of 107^°

D-space of [N(CH₃)₃(CH₂OH)]⁺:B3LYP/6-31G(d,P) level MO analysis file Link DOI:10042/161034

[N(CH₃)₃(CH₂CN)]⁺

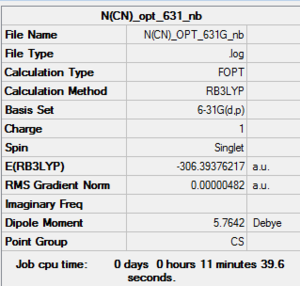
Optimisation of [N(CH₃)₃(CH₂CN)]⁺: B3LYP/6-31G level

D-space of [N(CH₃)₃(CH₂CN)]⁺ optimisation file Link DOI:10042/155621

Table 46 : Summary of [N(CH₃)₃(CH₂CN)]⁺ optimisation data

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000009 0.000015 YES RMS Force 0.000003 0.000010 YES Maximum Displacement 0.000052 0.000060 YES RMS Displacement 0.000015 0.000040 YES	Optimised molecule

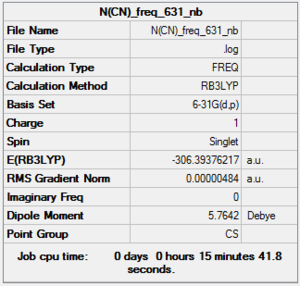
Frequency analysis of [N(CH₃)₃(CH₂CN)]⁺: B3LYP/6-31G level

D-space of [N(CH₃)₃(CH₂CN)]⁺ frequency file Link DOI:10042/155618

Table 47 : Summary of [N(CH₃)₃(CH₂CN)]⁺ frequency data

summary data	low modes
	Low frequencies --- -4.0768 -0.0009 -0.0004 0.0004 2.3693 3.6124 Low frequencies --- 91.8337 153.9482 212.0313

MO analysis of [N(CH₃)₃(CH₂CN)]⁺: B3LYP/6-31G level

D-space of [N(CH₃)₃(CH₂CN)]⁺ MO analysis file Link DOI:10042/161035

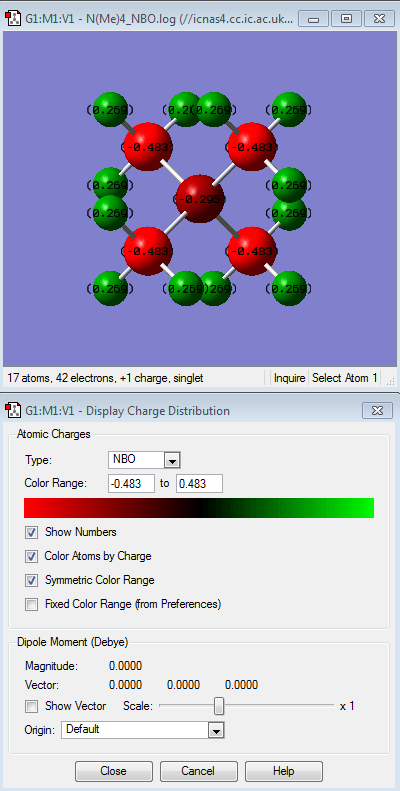
NBO analysis of [N(CH₃)₃(CH₂OH)]⁺ and [N(CH₃)₃(CH₂CN)]⁺ compared with [N(CH₃)₄]⁺

Table 48: Charge distribution analysis of different functional group effect

[N(CH3)4]+	[N(CH3)3(CH2OH)]+	[N(CH3)3(CH2CN)]+

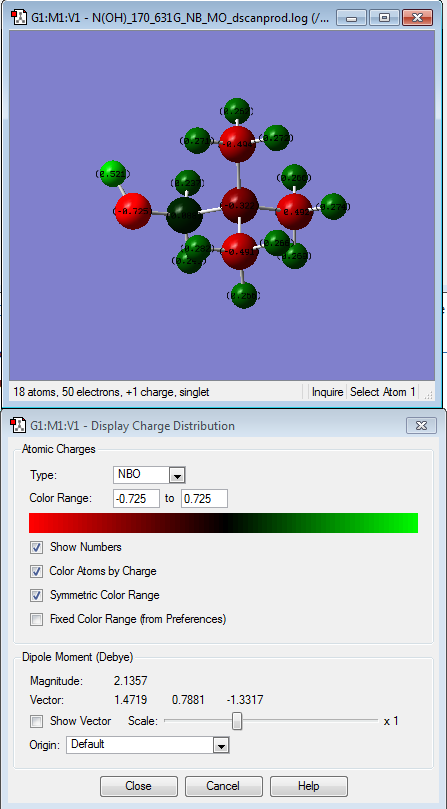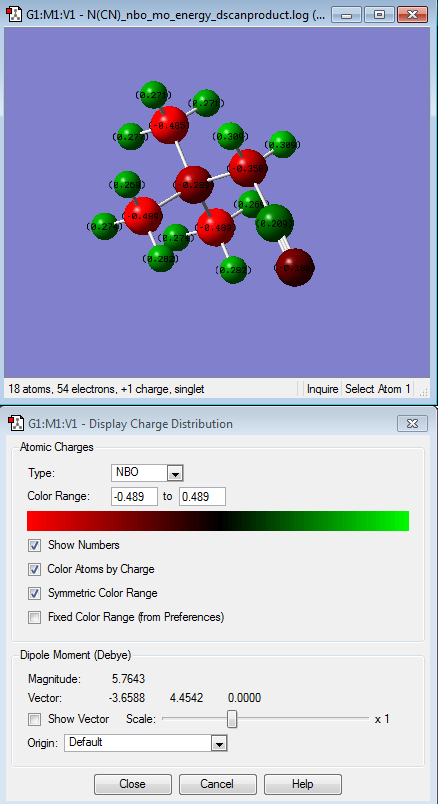
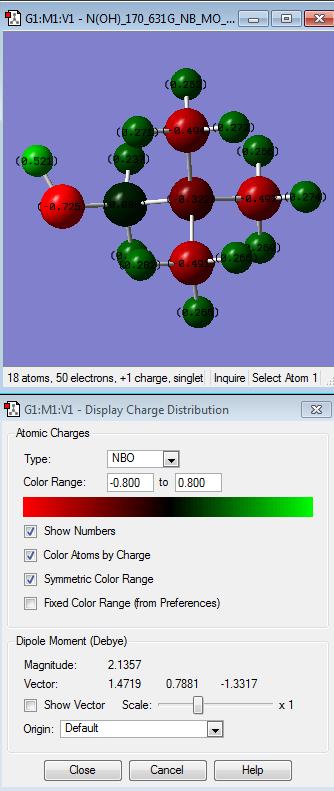
After comparing the charge distribution of [N(CH₃)₃(CH₂OH)]⁺, [N(CH₃)₃(CH₂CN)]⁺ and [N(CH₃)₄]⁺, it was found that the [N(CH₃)₃(CH₂OH)]⁺ has the largest charge range of -o.725 to + o.725. Therefore the charge range was modified for the next step in order

Table 49 : Comparing the charge distribution with same colour range

	[N(CH3)4]+	[N(CH3)3(CH2CN)]+	[N(CH3)3(CH2OH)]+
Specific NBO charges and Colour atom by charge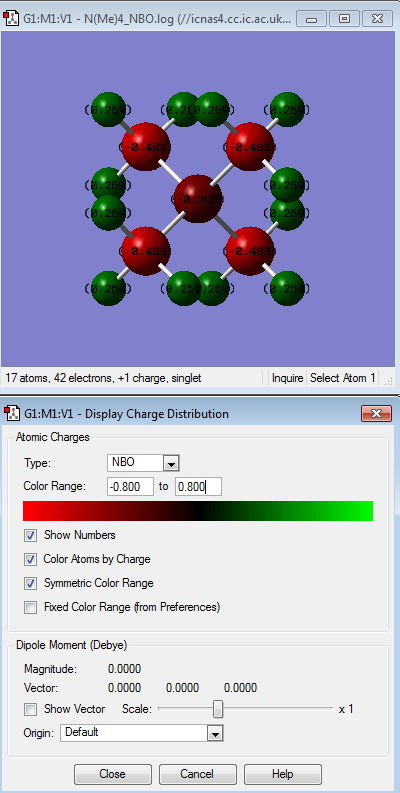

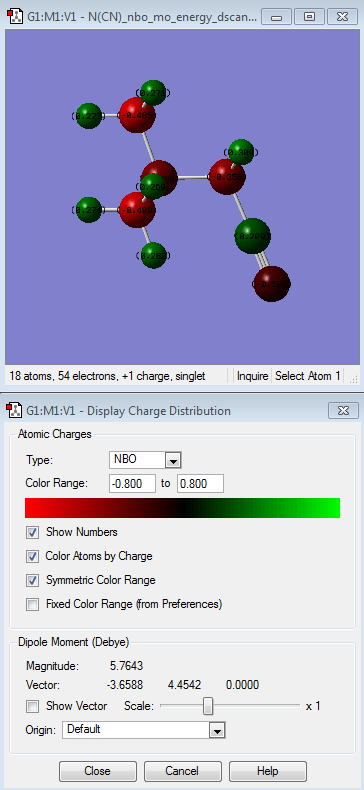Table 50: Comments on the 'colour by charge' diagrams

Molecule	Comments
[N(CH3)4]+	There is not a wide range of difference between the atoms where the most electropostively charged is the hydrogen atoms (indicated by the bright green colour) followed by nitrogen (dark red colour) and carbon being the most electronegative relative to the other atoms (indicated by its bright red colour). This contradicts the idea that N atom is more electronegative than C atom i.e. N= 3.0 while C=2.5 by Pauling scale. This might be due to H atoms donating its electron density to the C atoms.
[N(CH3)3(CH2CN)]+	The one that is interesting in here is the different relative electornegativity of the nitrogen atoms which depends on their neighbouring atoms. H atoms is the most relatively positive charge (indicated by the light green colour) followed by C atoms, then N atom (which connected to other methyl groups, the central N atom) and N (of the nitrile group) being the most electronegative atom relative to the other atoms in the molecule itself. This is due to CN being electron withdrawing group.
[N(CH3)3(CH2OH)]+	The hydrogen atom of the hydroxyl group is the most electropositive charged followed by H atoms of the methyl group then C atom (that is attached to the hydroxyl group), followed by N atom and lastly, C of the methyl groups. The hydrogen atom of the hydroxyl group is the most electropositive because while O atom is an electron-withdrawing group, thus takes the electron density of the hydrogen atom it is attached to.

Comparing HOMO and LUMO [N(CH₃)₄]⁺, [N(CH₃)₃(CH₂OH)]⁺, [N(CH₃)₃(CH₂CN)]⁺

Table 51 : HOMO-LUMO of [N(CH₃)₄]⁺, [N(CH₃)₃(CH₂OH)]⁺, [N(CH₃)₃(CH₂CN)]⁺

	[N(CH3)4]+	[N(CH3)3(CH2OH)]+	[N(CH3)3(CH2CN)]+
HOMO
LUMO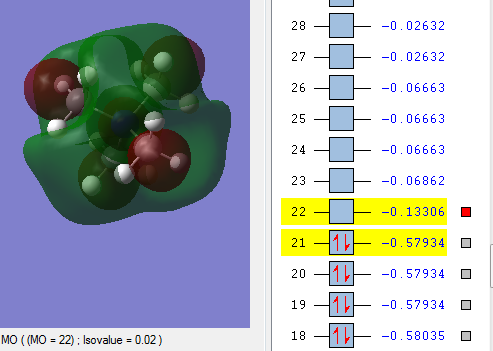
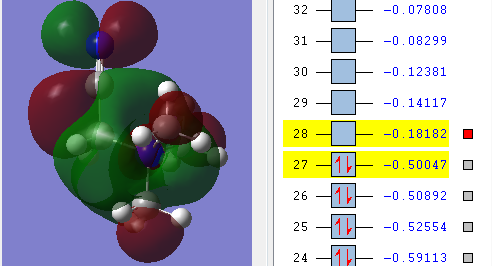
Energy difference between HOMO and LUMO	0.44628	0.36304	0.31865

In terms of the HOMO of the molecule;

Table 52 : Energy comparing the HOMO and LUMO of the ionic liquids

	[N(CH3)4]+	[N(CH3)3(CH2OH)]+	[N(CH3)3(CH2CN)]+
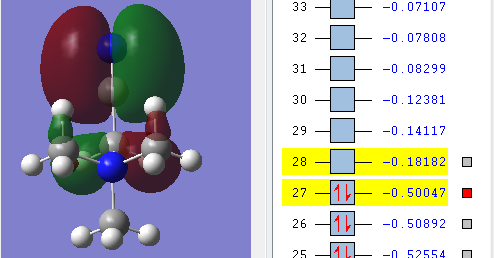
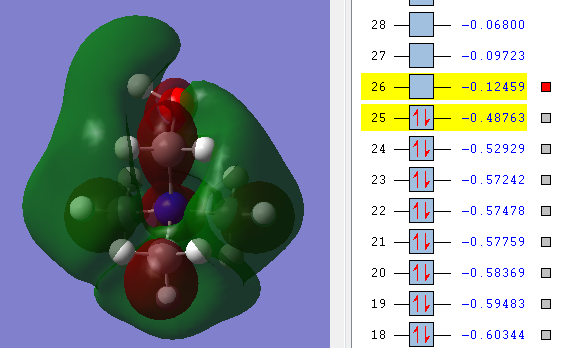
Energy of HOMO	The energy of the HOMO is the lowest in energy in comparison to the other molecules being compared, which indicates that [N(CH3)4]+ is the most bonding and thus less reactive relative to the other two molecules i.e 0.57934 a.u.	The energy of the HOMO is the highest among the molecule being compared i.e. 0.48763 a.u. and this makes the molecule reactive in comparison. Having an electron donating group and electron withdrawing group by induction shifted the energy of the HOMO up the most when compared with having just electron withdrawing functional group.	The energy of the HOMO is in the middle among the molecules being compared i.e. 0.50047 a.u. Having an electron withdrawing group shifted the HOMO energy up, causing it to be more reactive relative to with just [N(CH3)4]+.
Energy of LUMO	The energy of the LUMO is 0.13306 a.u. and this is the 'control' where the effect of having electron withdrawing and electron doanmting functional group is examined	The energy of the LUMO is 0.12459 a.u. The energy of the LUMO shifted up, making it more reactive as it is less stable	The energy of the LUMO is 0.18182 a.u. the energy of the LUMOn shifted down, thus it is more stable and less reacitive.
HOMO-LUMO gap	The HOMO-LUMO gap for [N(CH3)4]+ is 0.44628 a.u. which is the largest gap in comparison to the other two molecules. This means that large amount of energy is required to excite electron from ground state to its excited state thus signifies the stability of [N(CH3)4]+. Therefore [N(CH3)4]+ is least reactive among the molecules being compared.	The HOMO-LUMO gap for [N(CH3)3(CH2OH)]+ is 0.36304 a.u. which is in the middle compared with the [N(CH3)4]+ and [N(CH3)3(CH2CN)]+. OH being electron-donating group makes the molecules not as reactive as having CN as a functional group but it is still more reactive than [N(CH3)4]+	CN being electron-withdrawing functional group have the smallest energy gap between the HOMO and its LUMO, therefore it requires the least energy to excite electron from the ground state to the excited state. This causes them to be the least stable and thus the most reactive among the molecules being compared.

The HUMO and LUMO is called the frontier orbital which can be used to predict the chemical reactivity of the molecules. [[6]] In summary, the order of chemical reactivity (from more reactive to least reactive relative to each other) are [N(CH₃)₃(CH₂CN)]⁺ > [N(CH₃)₃(CH₂OH)]⁺ > [N(CH₃)₄]⁺ with respect to their HOMO-LUMO gap where large HOMO-LUMO gap signifies their stability as a molecule.

In terms of the shapes of the orbitals,

Table 53:

Molecule	Comments on the shape of the HOMO
[N(CH3)4]+	5 internuclear nodes i.e. 4 on the carbon atoms and 1 on the nitrogen atoms.
[N(CH3)3(CH2OH)]+	6 internuclear nodes, with 1 nodal plane through H-C-O-H. The HOMO of [N(CH3)3(CH2OH)]+ has the highest energy relative to the [N(CH3)4]+ and [N(CH3)3(CH2CN)]+.
[N(CH3)3(CH2CN)]+	5 internuclear nodes and 1 nodal plane through the nitrile group.

The higher the number of nodes or nodal, it causes the MO to be less bonding thus higher in energy and the result agrees with the energy level values.

Table 54:

Molecule	Comments on the shape of the LUMO
[N(CH3)4]+	The LUMO of [N(CH3)4]+ has the most delocalised electron density when compared with [N(CH3)3(CH2OH)]+ and [N(CH3)3(CH2CN)]+, therefore [N(CH3)4]+ is the most bonding MO (as evident by the energy level) and the most stable relatively thus the least reactive.
[N(CH3)3(CH2OH)]+	The shape of the HOMO is more diffuse around OH.
[N(CH3)3(CH2CN)]+	The shape of the MO is localised on the CN.

For molecule with electronegative substituent, for the molecule to be reactive, i.e. to be readily accept electron from a donor, the LUMO is preferably low in energy while the HOMO is high in energy.

In summary, the shapes of the orbital shows the effect of the functional group on the MO. The more electronegative the functional group i.e. CN in comparison to OH, the more localised the electron density in the functional group. The electron density is seen to be more diffuse in [N(CH₃)₃(CH₂OH)]⁺.

Conclusion

Table 55: Geometry Data

	BH3	BBr3	GaBr3
r(E-X)	1.19 Å	1.93 Å	2.39 Å
θ(X-E-X)	120.0 °	120.0 °	120.0°

Where E is the main group element and X is either H and Br with respect to the molecule analysed. The data from this table were obtained from the optimised molecules.

As shown in the table 1 above, changing the ligand H and Br will not change the point group of the molecule i.e. D₃h, a trigonal planar molecule with a bond angle of 120^°. The bond lengths of B-E (where E= H or Br) are different as we changed the ligand type to a more electronegative ligand i.e. Br, which is a weak field ligand.

Different central element have a significant effect on the bond length of the central atom to the ligand as shown in the table 1. While both Boron and Gallium have the bond angle which indicates that they have a trigonal planar structure thus D₃h point group, they are different in terms of their effect on the bond length.

Camparison of GaBr₃ and BH₃ molecules

GaBr₃ and BH₃ molecules vibration spectra were compared and it was found out that there is a large difference in the values of the frequencies of the GaBr₃ and BH₃ molecules. Both molecules were analysed under the same method B3LYP with basis set of 6-31G(d,p).

Table 56: Comparing GaBr₃ and BH₃ molecules

	GaBr3	BH3
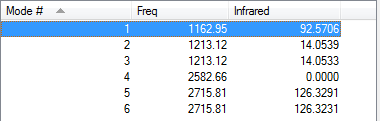
Frequency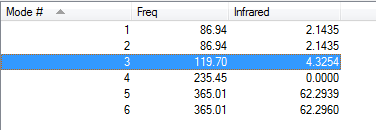
Displacement Vector
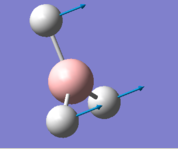
Modes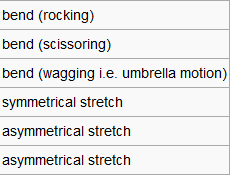

In the frequency row, the frequency of the umbrella motion is highlighted in blue as shown. For the modes of GaBr₃ and BH₃ molecules, the frequencies of the modes decreases down the column of the modes. Between these two molecules, the umbrella motion is an interesting part to discuss. As shown in the 'displacement vector' row of the table above, different atoms are doing the displacement. For the heavy molecule, GaBr₃ the Ga atoms were the one that is doing the displacement. This is due to the fact that Br atom are slightly heavier than Ga atom. For BH₃, the H atoms were the one doing the displacement as it is obviously lighter in mass in comparison to B atom. It is deduced then that for the umbrella motion, the lighter atom relative to the other atoms in the molecules will do the displacement. The arrangement of the modes between the two molecules were almost similar but the frequecy of the respective molecule's umbrella motion the focus of this discussion. Both the frequency and the intensity of this vibration varied greatly between these molecules. The frequency of these vibrational motion is proportional to the bond strength and inversely proportional to the mass of the molecule as shown by the Simple Harmonic Motion formula. Therefore since the mass of the GaBr₃ molecule is heavier in total in comparison to BH₃ molecule, the frequency is thus lower for the umbrella motion of the GaBr₃ molecule when compared with BH₃ molecule. The bond length of Ga-Br is 2.26 Å while for B-H it is 1.19 Å, therefore the longer the bond, the weaker the strength of the bond as evident by the dissociation energy of the bond.

Diagram 1 : Simple Harmonic Motion formula. ^[[1]]

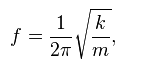
Traditional versus computational

[NR4]⁺ (R=Alkyl).

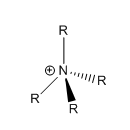
Traditionally, the positive charge on [NR4]⁺ molecule would be on the nitrogen centre but looking at the table above on the 'colour atom by charge' of [N(CH₃)₄]⁺, the green colour of the hydrogen atoms reflects the relative positive charge. The colour of the carbon atoms and the nitrogen having almost the same shade of red which reflects the relative δ^- of the atoms. Among nitrogen, carbon and hydrogen atoms, their relative electronegativity from highest to lowest are N(3.0), C(2.5) and H (2.1), thus hydrogen atoms are the most electropostive one and this is proven by the relative 'colour by charge' diagram shown in the above table. By computational method, the the positive charge is actually located on the hydrogen atoms. Traditionally, the formal postivite charge on the nitrogen atom represent the nitrogen donating its lone pair of electrons to form bond with the R group, in this case, methyl.

In conclusion, higher basis set used, the higher the accuracy as shown in BH₃ case and the closer the value is to the experimental value. Changing the ligand affects the frequency which depends on the size of the ligand and its mass. The heavier the ligand, the lower the frequency because frequency is inversely proportional to the mass as discussed previously.

In terms of functional group, using an eletron donating fucntional group decreases the HOMO-LUMO gap thus increase the molecule reactivity.

Further Study

Gaussian can also be used to predict the NMR of the molecules. It is interesting to use this to analyse computationally on how the chemical shift of a atom changes in different molecule environment, whether its different bonding type or different atoms its bonded to.

References

1. J. B. Foresman and A. Frisch, Exploring Chemistry with Electronic Structure Methods, Gaussian, Inc. U.S.A, 2nd Ed., 1993 and URL: http://hyperphysics.phy-astr.gsu.edu/hbase/shm.html for equation reference.

2. URL: http://www.wiredchemist.com/chemistry/data/bond-energies-lengths

3.URL: http://www.pearsonhighered.com/blbmw13einfo/assets/pdf/blbmw-ch09.pdf

4. URL: http://scitation.aip.org/content/aip/journal/jcp/96/5/10.1063/1.461942

5. URL: http://chemwiki.ucdavis.edu/Physical_Chemistry/Spectroscopy/Vibrational_Spectroscopy/Vibrational_Modes/Number_of_vibrational_modes_for_a_molecule