User:Ma7812
Introduction
Background
A transition state of a chemical reaction presents the geometrical configuration corresponding to a maximum in potential energy along the reaction coordinate. This can help to elucidate the pathway from reactants to products in a reaction and makes this point a particular focus of interest for both practical and theoretical chemists (And what is the difference in phenotype between these two species? João (talk) 12:43, 13 April 2015 (BST)). In the laboratory very fast methods such as femtosecond pulsed lasers are employed to cope with the very fast timescales involved in transition state formation and decay. Computational chemists often focus on the investigation of potential energy surfaces (PES) arising from quantum mechanical calculations. Locating those points of interest and comparison with experimental evidence can provide invaluable insights into the mechanisms and kinetics of a plethora of reactions. However, one ought to bear in mind that depending on which method is used the level of approximation can vary significantly. As a consequence the quantitative output can display large discrepancies and in many cases does not provide a direct correlation to data obtained from classical experiments. Computational chemistry can yield a useful understanding of the reactivity of the system under consideration, in this case the Cope rearrangement of 1,5-hexadiene and two examples of the Diels-Alder cycloaddition. However, just like for classical experiments the results have to be handled with care. The Gaussian program has been used to perform reaction models and calculations. Both of the above are pericyclic reactions with a circular movement of electrons in either direction with no clearly defined end or origin. The flow of σ and π electrons significantly alters the structure of the molecule and can play a major role in organic synthesis, the Diels-Alder reaction being one of the most important methods for the formation of 5 and 6 membered ring structures.
Methodology
For sizeable molecules exact mathematical solutions remain elusive, unlike 2 particle systems the dynamical equation cannot be solved for a large collection of atoms that compose the molecule under investigation. More specifically the separation of variables poses a problem 1. Computational methods often circumvent this issue by implementing an approximate separation of variables on the basis of physical attributes of the system, a prime example of this being the Born-Oppenheimer approximation which allows the separation of the motion of the electrons from the movement of the much heavier nuclei. This can provide noticeable simplifications and modelling the electronic wavefunction with respect to the nuclear position enables the construction of a potential energy surface for the nuclei. Both simple force field and molecular mechanics methods are brought to their limits when examining transition structures as the breaking and formation of bonds involved might not be accounted for using a single force field function 2. This also includes changing the nature of the bond, such as going from a single to a double bond and vice versa. Henceforth, electronic structure methods, more specifically independent particle models are employed for reactions such as the Cope rearrangement or the Diels-Alder cycloaddition. In the independent particle model the motion of other electrons is assumed to have no effect on any single electron, electron-electron interactions are generally accounted for by treating them as an average property of the system 1. A main methodology used in the calculations below is the Hartree-Fock method which is based on this framework. This can be divided into two subcategories, the ab initio form involving quantum mechanical derivation from the first principles and the semi-empirical method. The latter comprises the inclusion of parameters from experimental data, thus reducing the computational cost whilst the former requires a growing number of orbital determinants to improve the accuracy of the calculation. Both methods will be seen in the subsequent calculations. Basis sets form a further key component and their choice will depend on the basis function used and the size of the basis set 2. An increasing number of functions constituting one basis set will improve the accuracy of an individual calculation as we move towards a more complete set. Nevertheless, the computational cost is related to the size of the basis set, scaling with the 4th power. This necessitates a compromise between accuracy and computational expense 1. This can be partially alleviated by choosing a suitable basis function that constitutes a good representation of the molecular orbital. The Gaussian program used here predominantly employs Gaussian basis functions. This has the advantage over Slater basis functions that the integrals can be solved analytically and may be linearly combined to give good representations of the latter 2. The more facile solution of these integrals more than counterbalances the increased number of Gaussian basis functions needed and thus effectively reduces computational cost.
Results and Discussion
Background to the Cope Rearrangement
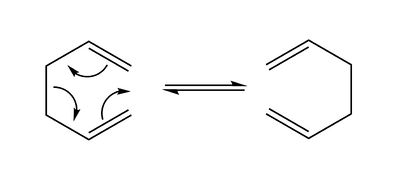
The Cope reaction, a [3,3] sigmatropic rearrangement, has been discovered in 1940 4. A simple example is shown in Figure 1 below. It is a pericyclic reaction involving 6 electrons, making it a 4n + 2, thermally allowed process proceeding via Hückel topology according to the Woodward-Hoffmann rules 5. The mechanism of this rearrangement has been investigated in a variety of both computational 6 and experimental 7,8 studies, for instance leading to the determination of concerted pathway. This reaction pathway involves transition states which closely resemble the boat and chair conformations of cyclohexane of which the chair conformation has been found to be more energetically stable 8. In this section both saddle points and local minima in the potential energy surface were determined using both the Hartree-Fock (HF) and Density Function Theory (DFT) methods. Furthermore, the activation energies of the Cope rearrangement were calculated and compared to experimental data.
The 3-21G Basis Set
The 3-21G basis set used is a Pople basis set, arising from the group of John Pople 9, as well as being a contracted basis set. The main advantage of this type of basis set is the reduction of computational cost by drawing focus away from the core orbitals 1. In chemical reactions it is predominantly valence electrons that determine the progress and outcome of the reaction making it justifiable to grant the valence orbitals a more significant share of the calculation. The priority of the core orbitals is decreased through isolating them and utilising a linear combination of functions to represent them rather than the variational principle (Is it not through the variational principle that one finds the optimal linear combination of basis functions? João (talk) 12:43, 13 April 2015 (BST)). Pople type orbitals involve either split (SV) or triply split valence. In this case, 3-21G, only two digits directly precede the capitalised 'G' meaning that it is a split valence basis set. The number of primitive Gaussian type orbitals, the complete collection of basis orbitals that is linearly combined to create the core orbitals, is given by the first number, 3. The number 2 specifies that 2 basic functions were used to represent the core atomic orbitals whereas one was used for the valence orbitals 2 (The core orbitals are represented by 3 contracted gaussians. The valence orbitals by a split valence set, with 2+1 functions. João (talk) 12:43, 13 April 2015 (BST)). The 'G' standing for Gaussian also acts as a divider between the basis functions appearing before and the polarised functions showing after it.
Setup and Calculation Results
The calculations were set up in Gaussview and the command windows for the Job type and method used in Gaussian are displayed in Figure 2 and 3 respectively. The structures were adjusted using the clean feature prior to submitting the job to Gaussian.
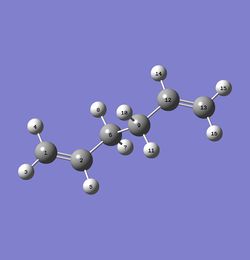
The first calculation for an antiperiplanar structure of 1,5-hexadiene yielded an optimised molecule shown in Figure 4 as anti3 and an energy of -231.68907066 Hartrees. The conversion factor from Hartree to kcal/mol was taken to be 627.509. The high number of significant figures was given as an indication of the validity of the obtained results. The conversion allows the determination of activation energies and direct comparison to experimental data which are presented in these units. The symmetrise function was subsequently applied and the point group was determined to be C2h. Symmetrising after performing an optimisation is generally not advisable as it alters certain parameters but gives a useful demonstration of the function in this instance (The point group editor in gaussview can be used to determine the point group of the molecule (or the higher symmetry group it is closest to) without changing its structure. João (talk) 12:43, 13 April 2015 (BST)). A second conformer with a gauche linkage was optimised. Using simple organic chemistry one would expect the anti-conformer to be slightly more stable on account of the dihedral angle of 180 degrees between the two vinyl groups. In the gauche structure the two vicinal groups are only separated by a torsion angle of 60 degrees making stereoelectronic repulsion more likely. Nonetheless, the energy found for the gauche conformer was marginally lower at -231.69266122 Hartrees. The more negative energy indicates a more stable structure as compared to the anti3 conformation. The symmetrise function gave a point group of C1 and the molecule is displayed as gauche3 in Figure 5 below.
Figure 4. The anti3 conformer of 1,5-hexadiene. |
Figure 5. The gauche3 structure of 1,5-hexadiene. |
Comparison of Minima
Conversion to units of kilocalories per mole shows that the energy difference is in fact relatively substantial at 2.253 kcal/mol. The fact that the results appear to contradict our expectations does not mean one should discard them. A possible explanation proposed by Rocque et al. was the formation of hydrogen bonding interactions between the π electrons of the alkene and the vinyl hydrogens having a stabilising effect 10. This type of interaction has been suggested for a variety of organic hydrocarbons 11. However, it remains questionable whether it is sufficient to account for the observed energy difference in light of the relatively low strength estimated for this type of interaction. For n-butane Widberg and Mucko have demonstrated that the anti-conformer is more energetically favourable by about 0.8 - 1.0 kJ/mol for each carbon-carbon linkage 12. The task of finding a global minimum among the possible conformation is aggravated by the fact that they are all very close in energy. There does not yet seem to be any conclusive evidence to decide for either one of the two. However, electron diffraction studies suggest the antiperiplanar conformation to be lower in energy 13. There are 27 possible conformations for 1,5-hexadiene yet only 10 of those are energetically distinct 10. To illustrate the numerous conformations, Newman projections adapted from Gung et al. 14 have been included as shown in Figure 6. One should note that D and F as well as J and L are two pairs of enantiomers. Just like the experimental results, the computational data appears to be inconsistent in some sense and the conformation Rocque et al. found at the same level of theory is different from the structure determined here. The global minimum of 1,5-hexadiene remains elusive and still poses a challenge to possibly be overcome by new computational methods. The energy differences are relatively minute in most cases which is not surprising as they only result from bond rotation around the three carbon-carbon single bonds present in the molecule. They arise from varying sterical interactions and stereoelectronic effects. For the supposedly most stable gauche3 conformation the unfavourable sterical effects are best compensated for by other stabilising interactions on account of the relative orientation of bonds. Given the proximity in terms of energy between all those antiperiplanar and gauche conformations one could argue that the Hartree-Fock method is not precise enough to characterise a global minimum. The neglect of electron correlation effects inherent to it might be one origin of the inconsistencies observed (What inconsistencies do you observe in your results? Do you mean inconsistencies comparing with other published data? João (talk) 12:43, 13 April 2015 (BST)). Another potential factor complicating the differentiation of the structures is, as mentioned above, the stabilisation of the gauche conformation via hydrogen bonding interactions (Hydrogen bonding in an hydrocarbon? João (talk) 12:43, 13 April 2015 (BST)).
(Well documented and pertinent discussion. João (talk) 12:43, 13 April 2015 (BST))

Local Minima
10 local minima were found on the PES in total using the HF/3-21G level of theory. The structure corresponding to anti2 in Table 1 was optimised giving an energy of -231.69253528 Hartrees being the third lowest found here. This was followed by symmetrising the molecule revealing the point group of the conformer as Ci. All other conformers have been discarded on account of being significantly higher in energy as compared to those 10, meaning that they were not true minima (Can't you have local minima which are high in energy? João (talk) 12:43, 13 April 2015 (BST)). The structures found and their corresponding energy as well as their point groups dare outlined in Table 1. These are useful to correlate or match different structures and define their symmetry.
Table 1: The optimisation results for the different conformers of 1,5-hexadiene using Hartree-Fock.
| Conformer | Structure | Point Group | HF - Energy (Hartrees) | Relative Energy (kcal/mol) | ||
| gauche1 |
|
C2 | -231.68771615 | 3.10 | ||
| gauche2 |
|
C2 | -231.69166702 | 0.62 | ||
| gauche3 |
|
C1 | -231.69266122 | 0.00 | ||
| gauche4 |
|
C2 | -231.69153032 | 0.71 | ||
| gauche5 |
|
C1 | -231.68961574 | 1.91 | ||
| gauche6 |
|
C1 | -231.68916013 | 2.20 | ||
| anti1 |
|
C2 | -231.69260235 | 0.04 | ||
| anti2 |
|
Ci | -231.69253528 | 0.08 | ||
| anti3 |
|
C2h | -231.68907066 | 2.25 | ||
| anti4 |
|
C1 | -231.69097055 | 1.06 |
The Density Functional Theory
Density Functional Theory (DFT) allows optimisation at a higher level of theory through bypassing several issues of the Hartree-Fock method, yet it requires significantly longer computational times. There are various approaches but the B3LYP, a semi-empirical method (One can indeed (perhaps not unanimously) call DFT a semi-empirical method. Why? Would this be true for all functionals? João (talk) 12:43, 13 April 2015 (BST)), has been shown to be one of the best in terms of the ratio between accuracy and computational cost. One main shortcoming of DFT is the lack of an arrangement that incorporates systematic convergence of the calculated results to approach an exact solution 1. However, usually the error imparted by this (What cause of error is being discussed here? João (talk) 12:43, 13 April 2015 (BST)) is quite small and the results very reasonable. A different basis set is used than before, 6-31G* as opposed to 3-21G in the Hartree-Fock calculation. It contains 6 rather than 3 primitive Gaussian type orbitals leading to a better representation of the core orbitals (But also of the valence orbitals. João (talk) 12:43, 13 April 2015 (BST)). The anti2 conformer was optimised using B3LYP/6-31G* level of theory, the energy obtained was -234.55970493 Hartrees. This is relevant for the determination of the activation energy for the Cope rearrangement as it was used as a reference.
Comparison of Geometries
In Table 2 the results from both the HF/3-21G and the B3LYP/6-31G* are compared with each other and experimental results from electron diffraction measurements 13 providing an external reference for the bond lengths to judge the quality of the obtained results (Good that you compared with experiment. João (talk) 12:43, 13 April 2015 (BST)). Figure 7 displays the structure with labelled atom numbering used for Table 2 and 3. Hartree-Fock theory seems to be slightly less accurate but there is no clear trend visible. It might also be worth noting that the angle between the sp2 and the sp3 carbon centres obtained for the DFT method is closer to 120 degrees than for HF Is there a reason to expect that the bond angles should be exactly 120º? João (talk) 12:43, 13 April 2015 (BST)).
(Overall how do the structures compare to each other? João (talk) 12:43, 13 April 2015 (BST))
Table 2: Comparison of the bond lengths from the two optimisation methods for the anti2 conformer.
| Atom labels | Bond Lengths (Å) from HF | Bond Lengths (Å) from DFT | Bond Lengths (Å) from Electron diffraction 13 |
|---|---|---|---|
| C1-C2 | 1.316 | 1.338 | 1.340 |
| C4-C6 | 1.509 | 1.507 | 1.508 |
| C6-C9 | 1.553 | 1.555 | 1.538 |
Table 3: Comparison of the bond angles from the two optimisation methods for the anti2 conformer.
| Atom labels | Dihedral Angle (°) from HF | Dihedral Angle (°) from DFT |
|---|---|---|
| C1-C4-C6-C9 | 114.669 | 118.797 |
| C4-C6-C9-C12 | -180.000 | -180.000 |
| C6-C9-C12-C13 | -114.669 | -118.797 |
Frequency Calculations
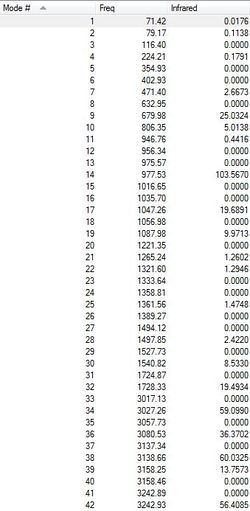
To confirm the result of an optimisation calculation as a true minimum a freqency calculation is a prerequisite. Therefore, for the anti2 molecule which had been optimised via the DFT method, a frequency calculation was carried out. The absence of imaginary frequencies is required. An imaginary frequency is negative as it corresponds to the second derivative of the energy of the PES which will be negative if there is a decrease in energy in some direction away from the point under consideration. Figure 8 shows the predicted IR spectrum arising from the calculated vibrations. There are only positive frequencies found for the optimised anti2 conformer as shown in Figure 8 implying that it is indeed a true minimum. It is also noteworthy that there are wavenumbers above 3000 cm-1 present which correspond to sp2 C-H stretches characteristic of unsaturated hydrocarbons such as the one considered here. If the vibration correlates to a change in dipole moment, the value shown under 'Infrared' will be non-zero. This calculation furthermore yielded thermochemical properties which are listed in Table 4. The sum of electronic and thermal energies are used for the calculation of the activation energy at a later stage. To investigate the effect of temperature the calculation was repeated at a temperature setting of 0.01 K, this was used as a reasonable approximation as Gaussian did not allow a temperature of exactly 0 K. As one would expect the thermal contribution decreased to zero, meaning all the sums were equal to the sum of electronic and zero-point energies. There is a zero point energy associated with all vibrational modes.
Table 4: Thermochemical properties of the anti2 conformer of 1,5-Hexadiene calculated using DFT.
| Energies | Calculation at 298.15 K(Hartrees) | Calculation at 0.01 K (Hartrees) |
|---|---|---|
| 1) Sum of Electronic + Zero-point Energies | -234.416256 | -234.416260 |
| 2) Sum of Electronic and Thermal Energies | -234.408962 | -234.416260 |
| 3) Sum of Electronic and Thermal Enthalpies | -234.408018 | -234.416260 |
| 4) Sum of Electronic and Thermal Free Energies | -234.447875 | -234.416260 |
The different energies include the following:
1) The potential energy at 0 K (E = Ee + ZPE, where ZPE denotes the zero point energy).
2) The energy at 298.15 K taking into account vibrational, rotational and translational energies (E = Ee + Etrans + Erot + Evib).
3) The enthalpy involves a modification by RT (H = E + RT).
4) The contribution of the entropy is also considered (G = H -TS).

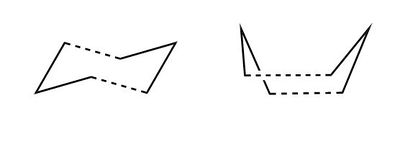
The Cope Rearrangement - Chair and Boat Transition States
2 different methodologies were used for each of the transition structures, for the chair conformation the Berny, named after computational chemist Berny Schlegel 15, as well as the redundant coordinate method, which effectively freezes certain coordinates, were utilised. The boat transition state was optimised using both the QST2 and QST3 techniques. The results obtained from the various methods were compared.
Berny Optimisation
A symmetrical allyl fragment with two bonds of order 1.5 was optimised using the Hartree-Fock method and then duplicated and arranged to model the chair transition state. A Berny optimisation yielded the chair structure via the calculation of force constants. 2.02069 Å was the distance between the bond forming carbon atoms obtained. The frequency calculation showed that an imaginary frequency was present at 818 cm-1 which is animated in Figure 12 indicating the simultaneous bond forming motion. This means the point corresponds to a maximum on the potential energy surface with respect to this direction but a minimum with respect to all others - a transition state.
Figure 11. The chair transition structure. |

Redundant Coordinates
The interatomic distance between the terminal carbon atoms on the allyl fragments involved in the bond formations was fixed to 2.20 Å. Considering the results from the Berny transition structure calculation the distance constraint appears plausible and should therefore provide a reasonable estimate. Subsequently the formation and breaking of bonds was computed by performing a TS optimisation with the bond distance no longer being set. Successful calculation resulted in the chair structure once more. The bond length was practically the same as before at 2.02075 Å showing that both method yield very comparable and reproducible outputs.
QST2 Method
Determination of minima on the PES is relatively straightforward process which proceeds via minimising the energy function until a local, potentially even a global, minimum is reached. The QST2 technique attempts to identify a transition state through the determination of maxima along the path between the minima corresponding to the reactants and products. This makes it so crucial to input both structures and take care to number the respective atoms correctly. The method effectively determines a set of characteristics that differentiate the reactants from the product and this is kept fixed throughout the optimisation whilst the other features are altered. This aspect of distinction is key and numerous differences may in fact deteriorate the result 1. Another prerequisite for successful calculation is the resemblance of both reactants and products with the transition state. The structure, that was used initially, failed and did not produce the outcome hoped for. Adaption of the reactants and products to a more boat like conformation then prompted successful detection of the boat transition state as shown in Figure 13. The distance between opposing terminal carbon atoms was found to be 2.14001 Å. The imaginary frequency at 840 cm-1 corresponding to the Cope rearrangement is visualised in Figure 14.
Figure 13. The boat transition structure obtained from QST2 calculation. |

QST3 Method
The QST3 method is an extension of the QST2 method which allows to use a guess transition structure as an input beside the reactant and the product structures. This means that the guess for the latter two does not have to be quite as accurate. Hence, the elongated hexadiene geometries which had previously failed for the QST2 calculation were used together with a guess transition structure. Whilst adjustment of the bond angles was required to permit a successful calculation for QST2, it proceeded without problem for QST3 yielding a very similar transition geometry to that obtained in the previous calculation. However, the distance between the terminal carbon atoms was now longer at just below 2.25 Å rather than 2.14 Å (This is a rather big difference. Would there be a zero on the first decimal place? João (talk) 14:45, 13 April 2015 (BST)). Hence, whilst this method is more lenient towards the provision of exact guess structures for the reactants and products one ought to take care when looking at the results.
Intrinsic Reaction Coordinates (IRC)
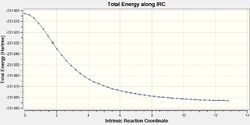
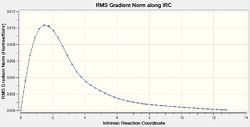
The IRC is very helpful for analysing the relevant section of the potential energy surface under consideration. The intrinsic reaction coordinate corresponds to the minimum energy pathway between reactants and products 1 and thus effectively provides means to investigate the chemically relevant aspect of the potential energy function. It can allow us to trace the path of the transition state as the product is formed which can be helpful as it may in many cases be difficult to determine the product conformation a certain transition structure leads to (Not only that, but also to determine what are the most important molecular motions along the reaction. João (talk) 14:45, 13 April 2015 (BST)) . This calculation was run at the same level of theory as the determination of transition states, Hartree-Fock using a 3-21G basis set, to remain consistent. The IRC method utilises the energy gradient to determine local minima by sequentially considering the points of steepest descent. For both the chair and boat transition states this analysis was performed, to ensure good results force constants were calculated at every step. For the chair TS the IRC calculation converged after 44 points despite specifying 50 points under the Job Type section in Gaussian. This was repeated using 100 points for calculation to confirm the accuracy of the result (If your calculation converged after 44 steps, why would you obtain a different result by increasing the total number of possible steps? João (talk) 14:45, 13 April 2015 (BST)). Again termination due to convergence occurred after 44 points. The same behaviour was observed for the boat transition structure only after 45 points. Whilst the conformer obtained for the chair appeared to be the gauche2 conformer found in Table 1 (cf. Figure 15), the boat transition state did not seem to resemble any of the previously obtained local minimum structures (What does the structure resemble to then? Did you try to optimize it further? Did the calculation converge? João (talk) 14:45, 13 April 2015 (BST)). Since the Cope rearrangement is thermoneutral, the same conformer should be observed whether the IRC path is followed in the forward or backward reaction. Hence, the calculation was only carried out in the forward direction. For the boat transition state the energy plotted against the intrinsic reaction coordinate and the RMS plot are displayed in Figure 16 and Figure 17. The same data for the chair TS is shown in Figure 18 and 19. Noticeable, the RMS gradient converges to a value in close proximity to zero as the calculation proceeds. Gauche2 was not the lowest energy conformation yet the IRC is unlikely to yield a global minimum as, given the information the algorithm has at its disposal, once a minimum is found it has no means of distinguishing a local from a global minimum. Interestingly, for the specified calculation involving the chair transition state, the gauche2 conformation was found irrespective of the number of steps employed or whether the obtained structure was used for a subsequent optimisation calculation at the same level of theory (For the same reason as before, why would you expect convergence to a different minimum, if you are already close to a local minimum? João (talk) 14:45, 13 April 2015 (BST)).
Figure 15. The chair transition structure resembling gauche2. |
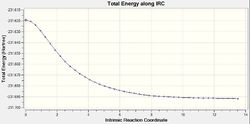
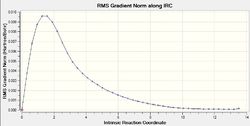
Activation Energies
To calculate the activation energies from the thermochemistry data obtained for the transition structures a reference was needed. This was taken to be the anti2 conformer as it was used as a starting point for the optimisation of the boat transition state. A single imaginary frequency was obtained for both the chair and the boat at both levels of theory. However, despite the relatively similar geometries, the activation energies are markedly different and the higher level of theory (DFT) yields more fitting results as evidenced by comparison to the experimental values. The transition state energies were recalculated, not the previously calculated ones reoptimised (Why did you choose not reoptimise the transition state? How do you know that the Hartree-Fock transition state structure is still a transition state at the higher level of theory? João (talk) 14:45, 13 April 2015 (BST)). Whilst the Hartree-Fock methods tends to overshoot the expected value, the B3LYP technique gives and underestimate. The experimental values are shown in Table 6 to the right with their associated error margin. In all cases the activation energies are slightly higher for the calculation at 0 K when compared to those at 298.15 K. This does not imply that the thermal energy provided simply allows to surmount the transition state barrier but rather indicates that thermal corrections have a more pronounced effect on the reactants than for the transition state (This is a very interesting observation. Would you have an idea why it would be so? Would it be general? João (talk) 14:45, 13 April 2015 (BST)). The overall quality of results is very satisfactory speaking for the accuracy and maybe even more importantly the reliability of these computational methods. This concludes the first part of the exercise having found 10 energetically distinct conformational minima of 1,5-hexadiene well in line with the literature, analysed the two possible transition states as well as having calculated the activation energy needed to cross each of the respective transition states.
Table 5: Energy values relevant for Activation Energy Calculations.
| Structure | HF - Electronic Energy (Hartrees) | HF - Sum of Electronic and Thermal Energies at 0.01 K (Hartrees) | HF - Sum of Electronic and Thermal Energies at 298.15 K (Hartrees) | DFT - Electronic Energy (Hartrees) | DFT - Sum of Electronic and Thermal Energies at 0.01 K (Hartrees) | DFT - Sum of Electronic and Thermal Energies at 298.15 K (Hartrees) |
|---|---|---|---|---|---|---|
| Chair | -231.61518689 | -231.466705 | -231.461345 | -234.50540757 | -234.362702 | -234.356766 |
| Boat | -231.60280243 | -231.450931 | -231.445294 | -234.49288972 | -234.351357 | -234.345043 |
| Anti2 | -231.69253528 | -231.539539 | -231.532565 | -234.55970464 | -234.416260 | -234.408962 |
Table 6: Comparison of Activation Energies.
| Transition state | HF - Activation energy at 0.01 K (kcal/mol) | HF - Activation energy at 298.15 K (kcal/mol) | DFT - Activation energy at 0.01 K (kcal/mol) | DFT - Activation energy at 298.15 K (kcal/mol) | Experimental value at 0 K (kcal/mol) |
|---|---|---|---|---|---|
| Chair | 45.703991 | 44.691191 | 33.608127 | 32.753460 | 33.5 (±0.5) |
| Boat | 55.602317 | 54.763338 | 40.727217 | 40.109748 | 44.7 (±2.0) |
The Diels-Alder Reaction
Frontier Molecular Orbital Theory
Frontier Molecular Orbital (FMO) theory is a valuable method to qualitatively predict the outcome of chemical reactions. It is based on considering the interaction between the orbitals of the reactants and the products with a strong focus on the HOMO and LUMO interaction. According to basic Molecular Orbital (MO) theory a chemical reactions between two molecules is likely to proceed if the interacting orbitals are close in energy and there is a significant degree of in-phase overlap. The former is determined by the nature of the reactants while the latter is affected by symmetry considerations and governs to which degree the overlap is favourable. The Diels-Alder reaction between butadiene and ethene exhibits normal electron demand in which case the LUMO of the dienophile, ethylene in this case, interacts with the HOMO of the diene. Both of these orbitals are antisymmetric with respect to a central plane going through the center of both reactants as visualised in Figure 20. The electron demand could be inversed by placing electron donating substituents on the dienophile and/or electron withdrawing groups on the diene.

Woodward-Hoffmann Rules for Pericyclic Reactions
Since cycloadditions are a subcategory of pericyclic reactions the Woodward-Hoffmann rules provide a useful method to predict whether a given case is allowed or disallowed under thermal or photochemical conditions 5. They are based upon the conservation of orbital theory. The Diels-Alder reaction under consideration here is a thermally allowed cycloaddition with suprafacial topology involving 4n+2 electrons. This means there is good correlation between the relevant HOMO and LUMO orbitals and no substantial barrier has to be overcome under thermal conditions.
The Simple Diels-Alder Reaction
Cis-butadiene was optimised using the semi-empirical molecular orbital method AM1 (Austin Model 1), the point group being C2v. The HOMO and LUMO orbitals of this reactant were mapped out as shown in Figures 22 to 25. Both surface and mesh views are provided for each. As can be easily seen from those plots, the HOMO is antisymmetric with respect to a plane intersecting the central carbon-carbon bond standing orthogonal to the plane of the molecule. In contrast, the LUMO is symmetric with respect to said plane.
Figure 21. The AM1 optimised structure of cis-butadiene. |
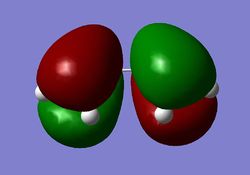



The first cycloaddition considered here is a simple pericyclic reaction between cis-butadiene and ethene outlined in Figure 26. The product formed in this reaction is cyclohexene as a Diels-Alder adduct. The transition state of the reaction was calculated using the AM1 level of theory again producing the geometry displayed in Figure 27. This was confirmed to be a true transition structure by performing a frequency calculation which yielded a single imaginary frequency which is visualised in Figure 28. This nicely shows the concerted bond forming and breaking involved in this pericyclic reaction. The imaginary frequency incorporates the motion of carbon atoms relevant to the synchronous bond formation and thus gives a useful idea about the progress of the reaction. The lowest positive frequency, as shown in Figure 29, however, does not appear to have any relevance to the advancement of the reaction. It might be interpreted to imply sequential bond formation as ethene appears to approach one carbon first then the other, yet this vibration does not correspond to the bond formation in the transition state owing to its position on the potential surface. One ought to differentiate here between the lowest frequency and the ground state, all modes can simultaneously be on the ground state. The HOMO and LUMO orbitals were determined again and surface as well as mesh views are shown in Figures 30 to 33. As before the HOMO is antisymmetric with respect to the central plane whilst the LUMO is symmetric. The distance between the terminal carbon atoms, between which bonds are being formed, was found to be 2.12 Å. The van der Waals radius of the carbon atom is generally stated to be 1.70 Å 17, meaning that the C-C separation lies well below the sum of two van der Waals radii. This implies that there is favourable interaction in the form of attractive forces at this range that drive the creation of the partially formed σ bond forward. All bonds that initially were double bonds, i.e. all except the central C-C bond in cis-butadiene, have a bond length of approximately 1.38 Å with the remaining bond having a distance of 1.40 Å. Compared to the typical double bond length of 1.34 Å and single bond separation of 1.54 Å 16, the distances observed do neither conform to those of sp2 nor those of sp3 carbon centres but rather seem to correspond to an intermediate between the two. It is also noticeable that the bond lengths are very similar, indicating again that this is a concerted reactions where the bond shortening and elongation proceeds simultaneously. The HOMO of the Diels-Alder adduct is created by combination of the HOMO of the diene and the LUMO of the dienophile (cf. Figures 20, 23 and 31).
(How about the other frontier orbital? What are their symmetry properties? João (talk) 16:37, 13 April 2015 (BST))
Figure 27. The transition state of the cycloaddition calculated via AM1. |


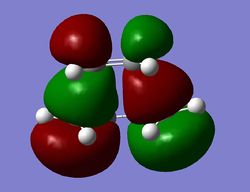

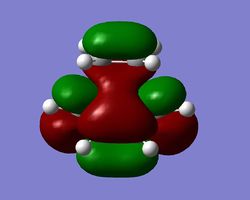

Diels-Alder - Activation Energy
Using the AM1 semi-empirical level of theory, the energies for ethylene, cis-butadiene and the Diels-Alder adduct were computed using a frequency calculation at 298.15 K and utilised to find the activation energy of the reaction. The sum of thermal and electronic energies were established to be as follows (values in Hartrees): Ethene = 0.080252, cis-butadiene = 0.138573 and the transition structure = 0.259453. Subsequent substraction and conversion to kilocalories per mole yielded an activation energy of 25.494436 kcal/mol. This compares favourably to the value of 27.5 (± 2) kcal/mol quoted in the literature 18,19, the potential error in both directions is given in brackets. The good fit despite the fact that a relatively low level of theory is used as compared to B3LYP for instance can be accounted for that this is a semi-empirical method. This means that the parameters will to some extent be based on empirical values. Therefore, this method is likely to reproduce values in proximity of the experimental input.
Diels-Alder - Regioselectivity

Exo and Endo - Optimisation
The Diels-Alder reaction between 1,3-cyclohexadiene and maleic anhydride is investigated in this section. The product of this thermally allowed cycloaddition proceeding via suprafacial topology as before is bicyclo[2.2.2]oct-5-ene-2,3-dicarboxylic anhydride.
Figure 35. The AM1 optimised structure of 1,3-cyclohexadiene. |
Figure 36. The AM1 optimised structure of maleic anhydride. |
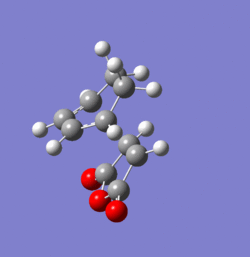
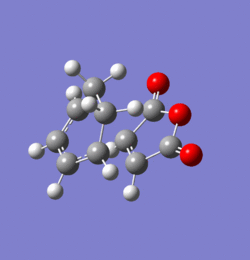
The transition states for the exo and endo products of this reaction were found using the frozen coordinate method at the AM1 level of theory. Both were confirmed as true transition structures by the presence of a single imaginary frequency. These are animated in Figures 37 and 38 respectively and clearly imply simultaneous bond formation on both ends of the fragments as one would expect from this type of concerted cycloaddition. The energies of the respective TS and their structural data are shown and compared in Tables 7 and 8 respectively. The distance between the bond forming carbon atoms is slightly higher in the exo than in the endo case. The distance between the carbonyl carbon and the sp2 fragment of the endo structure is approximately the same as the separation between the selected carbonyl centre and the sp3 fragment of the exo structure. Since the tetrahedral carbon centres are more sterically demanding this will induce an unfavourable repulsion which destabilises the exo transition structure relative to the endo one. It has also been suggested that van-der Waals interaction play some role in determining geometry of the transition state 20. Since the transition state of the endo structure has a lower energy, this will be the product formed under kinetic conditions. However, the exo product suffers from less unfavourable steric interaction and is therefore the molecule formed under thermodynamic conditions. Overall, it can be seen that the endo TS is favoured by approximately 0.75 kcal/mol at 298.15 K.
Figure 39. The AM1 optimised endo transition structure. |
Figure 40. The AM1 optimised exo transition structure. |
Exo and Endo - Comparison
Table 7: Endo and exo energies compared.
| Exo - Electronic energy (Hartrees) | Endo - Electronic energy (Hartrees) | Exo - Sum of Electronic and Thermal Energies at 298.15 K(Hartrees) | Endo - Sum of Electronic and Thermal Energies at 298.15 K(Hartrees) |
|---|---|---|---|
| -0.05041981 | -0.05150479 | 0.144882 | 0.143684 |
| Difference in electronic energy (Hartrees) | Difference in electronic energy (kcal/mol) | Difference in electronic and therrmal energies (Hartrees) | Difference in electronic and therrmal energies (kcal/mol) |
| 0.001085 | 0.680835 | 0.001198 | 0.751756 |

Table 8: Endo and exo geometries compared.
| Endo - Atom labels | Bond Lengths (Å) | Exo - Atom labels | Bond Lengths (Å) |
|---|---|---|---|
| C1-C2 | 1.49051 | C1-C2 | 1.48975 |
| C2-C3 | 1.52291 | C2-C3 | 1.52209 |
| C3-C4 | 1.49053 | C3-C4 | 1.48979 |
| C4-C5 | 1.39307 | C4-C5 | 1.39440 |
| C5-C6 | 1.39726 | C5-C6 | 1.39677 |
| C6-C1 | 1.39304 | C6-C1 | 1.39432 |
| C15-C19 | 1.48924 | C15-C19 | 1.48824 |
| C19-C18 | 1.40848 | C19-C18 | 1.41010 |
| C18-C17 | 1.48926 | C18-C17 | 1.48822 |
| C4-C18 | 2.16227 | C1-C18 | 2.17060 |
| C1-C19 | 2.16248 | C4-C19 | 2.17014 |
| C5-C17 | 2.89241 | C2-C17 | 2.94513 |
The HOMO and LUMO orbitals for both transition structures which can be constructed from the frontier orbitals of the reactants are plotted in Figures 43 through to 50. Following modern theory a secondary orbital effect should be in place and visible for the endo transition structure as it plays a major role in the explanation as to why this is favoured under kinetic conditions. However, the HOMO does not seem to exhibit overlap between the carbonyl based orbitals and the relevant carbon-carbon double bond in 1,3-cyclohexadiene. This might seem surprising but one ought to consider the filled orbitals below the HOMO. In fact the HOMO-1 (second highest filled orbital) does clearly show in phase correlation between the mentioned orbitals. These are not present to any comparable extent in the exo form. As expected the orbital energy of the HOMO-1 is lower for the endo than the exo transition structure. All of this is in line with the theoretical expectations concerning the secondary orbital overlap. However, how pronounced this contribution is and how dominant it is compared to, for instance sterical considerations, is another question. The endo orbital layout is visualised in Figure 51.

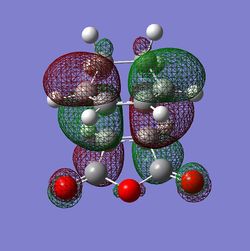
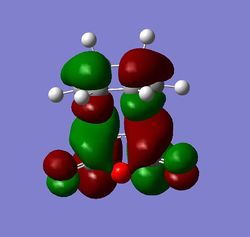

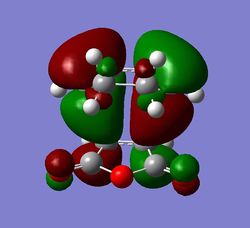
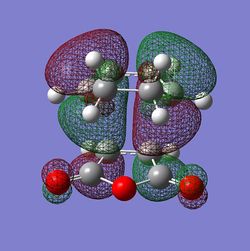
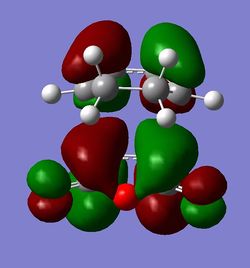
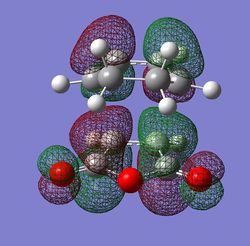

Endo and Exo - Activation Energies
The activation energies for both transition states are outlined in Table 9. They were determined from the thermochemistry data obtained from the frequency calculation at AM1 level of theory. Once more it can be seen that the endo state is slightly more favourable making it the kinetic pathway. Under equilibrating conditions, however, the small difference in energy is unlikely to be a major factor. One should also note that that there is a noticeable deviation from the experimental value for the activation energy of the Diels Alder reaction of 11.4 kcal/mol 21. This may be explained by the fact that not a high level of theory is used and a series of approximations is made in the computation. The Austin Model 1 is based on the Neglect of Differential Diatomic Overlap (NDDO) integral approximation which uses a zero-differential orbital approximation and simplifies two-centre charge repulsions 22,23. One key issues of this method is the fact that it does not sufficiently account for the rotational barrier imposed upon bonds which exhibit double bond character to some degree, for butadiene for instance the deviation is just below 5 kcal/mol 1 which is a very significant error. Furthermore, it tends to overestimate the stability of alkyl groups, has issues with accurately predicting van-der-Waals interaction and the geometry involved in hydrogen bonding. These may all have contributed to the discrepancy of the calculated values from the experimental ones observed in this section, the most marked one being the activation energy below.
Table 9: Endo and exo activation energies (AM1).
| Structure | Sum of Electronic and Thermal Energies at 298.15 K (Hartrees) | Activation Energy (kcal/mol) |
|---|---|---|
| Maleic Anhydride | -0.058192 | - |
| 1,3-cyclohexadiene | 0.157726 | - |
| Endo | 0.143684 | 27.704522 |
| Exo | 0.144882 | 28.456278 |
The same data has been obtained via DFT/B3LYP for comparison as shown in Table 10. The activation energies are much closer to the experimental value, most likely owing to the fact that a higher level of theory with increased computational cost was used.
(Good thing that you obtained the DFT value. Did you reoptimise the transition state geometry? João (talk) 16:37, 13 April 2015 (BST))
Table 10: Endo and exo activation energies. (B3LYP)
| Structure | Sum of Electronic and Thermal Energies at 298.15 K (Hartrees) | Activation Energy (kcal/mol) |
|---|---|---|
| Maleic Anhydride | -379.228563 | - |
| 1,3-cyclohexadiene | -233.288711 | - |
| Endo | -612.491827 | 15.968222 |
| Exo | -612.487655 | 18.586189 |
Conclusion
The Gaussian program was used to investigate the Cope rearrangement and the Diels-Alder reaction, the results were visualised using Gaussview. This was done at various levels of theory which often showed noteworthy differences in terms of accuracy and several methods to analyse the transition state geometry were employed. Overall, the density functional theory (DFT), more specifically B3LYP appeared to yield the best results when compared to experimental data. This is not overly surprising given that it is probably the most sophisticated modelling method used here. The PES was examined with respect to minima, which were confirmed by the presence of solely positive vibrations, and transition states that were validated by the existence of a single imaginary frequency. The numerical results were generally satisfactory, in certain cases even spot on, and the visualisation of the orbitals in the Diels-Alder reaction made it possible to qualitatively detect the secondary orbital effect in place. All of these parameters provide valuable insights and could potentially be very useful to analyse the reactivity and chemical behaviour of a set of molecules under given conditions. For the Cope rearrangement it was possible to order all the 10 energetically distinct conformers of 1,5-hexadiene and detect gauche3 as the most stable one. On top of this, the boat and chair transition states were characterised and the pathways leading to them analysed, the chair conformation was distinguished by its lower activation energy thus being the preferred TS. The molecular orbitals of the model Diels-Alder reactions could also be studied well in terms of energy, symmetry and their effect on the relative stabilities of the transition structures. Having looked at a sufficient number of reactants it may even be possible to detect certain characteristics or trends in their PES and potentially predict reaction outcomes. Further work on this topic could involve looking at a wider variety of examples for both pericylic reactions and investigate the effect of different substituents and structural features. In addition, the information gained on these reactions this could prove helpful in terms of adapting and optimising the computational methods in order to receive even more accurately calculated parameters and orbital models.
References
1. F. Jensen. Introduction to computational chemistry. John Wiley & Sons, 2013.
2. M. J. Bearpark, A. Simperler, Lectures 1-3, QM3 Quantum Mechanics 3, Imperial College London, 2014.
3. http://www.gaussian.com/g_tech/g_ur/m_basis_sets.htm (Gaussian user manual), accessed on 24th March 2015.
4. A. C. Cope, E. M. Hardy, J. Am. Chem. Soc, 1940, 62(2), pp 441-444.
5. R. B. Woodward, R. Hoffmann, Angew. Chem. Int. Ed., 1969, 8(11), pp 781-932.
6. O. Wiest, K. A. Black, K. N. Houk, J. Am. Chem. Soc., 1994, 116, pp 10336-10337.
7. W. von Doering, V. G. Toscano, G. H. Beasley, Tetrahedron, 1971, 27, pp 5299-5306.
8. W. von Doering, W. R. Roth, Tetrahedron, 1962, 18, pp 67-74.
9. J. S. Binkley, J. A. Pople, W. J. Hehre, J. Am. Chem. Soc., 1980, 102, pp 939-947.
10. B. G. Rocque, J. M. Gonzales, H. F. Schaeffer III, Mol. Phys., 2002, 100(4), pp 441-446.
11. Y. Umezawa, S. Tsuboyama, H. Takahashi, J. Uzawa, M. Nishio, Tetrahedron, 1999, 55, pp 10047-10056.
12. K. B. Widberg, M. A. Murcko, J. Am. Chem. Soc., 1988, 110, pp 8029-8038.
13. G. Schultz, I. Hargittai, J. Mol. Struct., 1995, 346, pp 63-69.
14. B. W. Gung, Z. H. Zhu, R. A. Fouch, J. Am. Chem. Soc., 1995, 117(6), pp 1783-1788.
15. H. P. Hratchian, X. Li, J. Chem. Theory. Comput., 2012, 8(12), pp 4853-4855.
16. F. H. Allen, O. Kennard, D. G. Watson, L. Brammer, A. G. Orpen, R. Taylor, J. Chem. Soc., Perkin Trans. 1987,2, S1-S19.
17. R. S. Rowland, R. Taylor, J. Phys. Chem., 1996, 100(18), pp 7384-7391.
18. E. Goldstein, B. Beno, K. N. Houk, J. Am. Chem. Soc., 1996, 118, pp 6036-6043.
19. D. Rowley, H. Steiner, Discuss. Faraday Soc. 1951, 10, pp 198-213.
20. Y. Kobuke, T. Sugimoto, J. Furukawa, T. Fueno, J. Am. Chem. Soc., 1972, 94(10), pp 3633-3635.
21. R. A. Grieger, C. A. Eckert, J. Am. Chem. Soc., 1970, 92(24), pp 7149-7153.
22. http://en.wikipedia.org/wiki/Austin_Model_1, accessed on 25th March 2015.
23. http://en.wikipedia.org/wiki/NDDO, accessed on 26th March 2015.
24. J. Clayden, N. Greeves, S. Warren, and P. Wothers, Organic Chemistry, Oxford University Press, New York, 2nd edition, 2012.
25. P. Atkins, J. de Paula, Physical Chemistry, Oxford University Press, Oxford, 9th edition, 2010.
