User:Jp1713

All log files can be seen in the link here

Introduction

What is the purpose of using computational chemistry to determine the preferred pathway of an organic reaction?

It is not possible to analyse the physical properties of short-lived transition states without the use of computational chemistry.

Computational chemistry can determine a reaction's pathway by considering and predicting the activation energy of it's transition state.

This computational experiment will study three pericyclic reactions using GaussView 5.0.

The Cope rearrangement of 1,5- hexadiene will be investigated in the tutorial section. Both the Diels-Alder reactions of cis-butadiene and ethene and then cyclohexa-1,3-diene will be investigated in the exercise section.

By looking at Potential Energy Surfaces (PES), this experiment aims to locate the transition state structures of the above reactions. This experiment will determine through which of these structures the reactions will proceed.

This will be done by application of the Born-Oppenheimer approximation and using the Schrodinger equation:

$E\psi =\hat{H}\psi$

to calculate activation energies of these structures.

Gaussian is able to compute the relationship between geometry and energy of a reaction using the 3D PES. Transition states relate to the maxima of the plots on the PES and intermediates relate to the minima. The program achieves this by calculating the electrostatic interactions between two or more reacting nuclei.

Three methods are used in this experiment in this experiment's calculations: HF / 3-21 G, DFT / 6-31 G and Semi-Empirical AM1 (HF stands for Hartree Fock and DFT stands for Density Function Theory). These methods use the Born-Oppenheimer approximation (as explained above). HF fails to consider the interactions of electrons; DFT is a higher level of theory and considers the density and behaviour of electrons. The Semi-Empirical AM1 method is much faster than the method it originates from, HF. It is used when simulating more complex reactions but there are several downsides. These will be discussed later in the experiment wiki.

Nf710 (talk) 15:42, 11 February 2016 (UTC)HF methods are more advanced than DFT, you are just using a higher basis set. it fails to account for electons of the same spin in the same spacial orbital as they can essentially exist in the same place and are therefore not correlated there have a higher colomb repulsion terms. they also feel a mean field from all the other electrons.

Cope Rearrangement Tutorial

Introduction

The Cope Rearrangement will be examined in this tutorial.

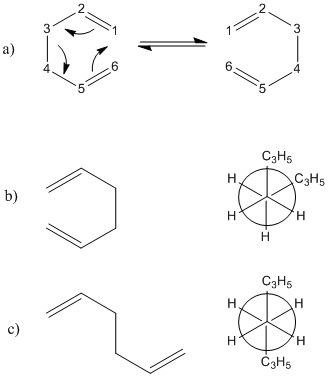
In this organic pericyclic reaction, a concerted process takes place in which a σ bond is broken at the same time as another σ bond is formed. This can be referred to as a [3, 3]-sigmatropic rearrangement. As a consequence of the free rotation about carbon-carbon single bonds, the molecule 1, 5-hexadiene is able to adopt a variety of conformations. 1, 5-hexadiene can adopt conformers called anti- and gauche- ,

This tutorial will optimise these two conformers to HF/3-21 G and B3LYP/6-31 G* (DFT) and calculate their energies. In the experiment below the lowest energy and most stable conformation was found to be the gauche3.

Th is reaction can occur via two transition structures: the chair transition structure and the boat transition structure. By calculation of the energies of the individual transition state structures, it is possible to determine through which transition state structure the reaction will proceed through. the This will ultimately define the preferred reaction pathway.

a) Cope rearrangement, b) antiperiplanar conformation and newman projection, c) gauche conformation and newman projection

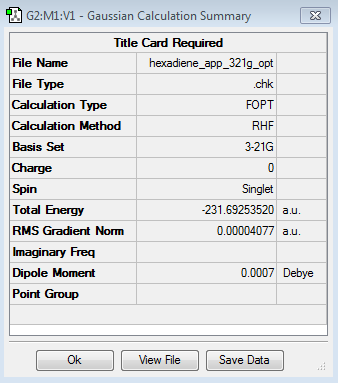
1,5-hexadiene antiperiplanar conformer optimisation

The antiperiplanar conformation of the 1,5-hexadiene was drawn in GaussView 5.0. The molecule's dihedral angle was changed to 180° in order to maximise the distance between the two double bonds. The structure was cleaned and symmetrized and then optimised using the HF level of theory and the 3-21 G basis set.

The energy of the molecule was found to be -231.69253520 a.u. and the point group was determined to be Ci. The corresponding structure is anti2.

It is worth noting (for energy values a.u.) that though values to 8 decimal places have been given, only the first 6 decimal places are not affected by background noise in during the calculations

The table below shows the Jmol of the molecule, a summary of the results and the point group:

Structure	Calculation Summary	Point Group
		Ci

1,5-hexadiene gauche conformer optimisation

The gauche conformation of the 1,5-hexadiene was drawn in GaussView 5.0. The molecule's dihedral angle was changed to 60°. The structure was cleaned and symmetrized and then optimised using the HF level of theory and the 3-21 G basis set.

The energy of the molecule was found to be -231.68771617 a.u. and the point group was determined to be C2. The corresponding structure is gauche1.

The table below shows the Jmol of the molecule, a summary of the results and the point group:

Structure	Calculation Summary	Point Group
		C2

Comparing the anti- and gauche- energy values

anti-: -231.69253520 a.u

gauche-: -231.68771617 a.u.

It can be seen that the lower energy conformer is the anti- conformer.

On examination of the structures, it can be seen that the terminal carbon atoms in the gauche conformer are as close together as possible, increasing steric clashes and therefore increasing the conformer's energy.

On the other hand the anti- conformer’s structure reduces steric clashes between the terminal carbon atoms. Electronic stabilisation through hyperconjugation is also present in the anti- conformer.

Both of these considerations contribute to a lower energy conformation.

It is possible to compare the optimised conformers with the structures in Appendix 1 . By comparison of the energies, the antiperiplanar structure corresponds to the anti2 conformer (7 significant figures) and the gauche structure corresponds to the gauche1 conformer (7 significant figures).

The energies of the conformers both matched those in Appendix 1 to a good degree of accuracy, so to conclude, both optimisations were successful

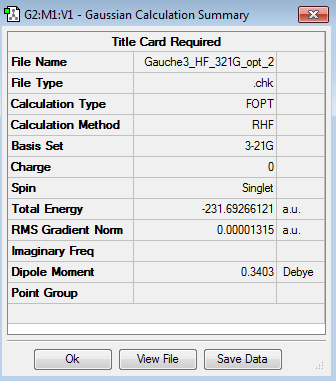
1,5-hexadiene gauche3 conformer optimisation: lowest energy conformer

So far, only two conformers have been generated and it is worth noting that the potential energy surface of 1,5 hexadiene possesses more then two minima. With this in mind, is worth investigating other conformers to see if a lower energy conformer exists.

It was found that the lowest energy conformer in Appendix 1 is the gauche3 conformer (Relative Energy: 0.00 kcal/mol). The energy and point group of the molecule are -231.69266 a. u. and C1 respectively.

This conformer was drawn on GaussView 5.0. The energy was found to be -231.69266121 a.u. and the point group was determined to be C1, the same as in the Appendix, therefore the optimisation was successful.

The table below shows the Jmol of the molecule, a summary of the results and the point group:

Structure	Calculation Summary	Point Group
		C1

An observation can be made: the lowest energy conformer is gauche which this disagrees with the previous section where the low energy of the anti conformer was rationalised using steric and electronic reasons.

In the gauche3 conformation, steric and therefore electronic clashes between terminal hydrogens in the molecule are minimised. Despite this, the molecule still maintains a good in phase overlap between the π orbitals on the terminal carbon-carbon double bonds. This molecule contains favourable secondary orbital overlap .

The π orbital of the second last carbon has a favourable interaction with a vinyl proton on the adjacent carbon.

By visulising the filled HOMO, it is possible to see the two stabilising stereoelectronic interactions. An image of the HOMO can be seen below:

image of the filled HOMO

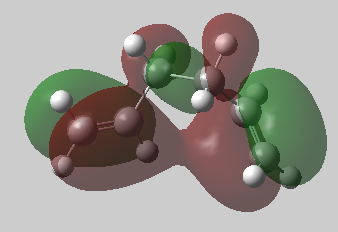
Nf710 (talk) 15:45, 11 February 2016 (UTC) Excellent use of the orbitals to explain the energy.

1,5-hexadiene antiperiplanar conformer re-optimisation

In the first section: 1,5-hexadiene Antiperiplanar conformer optimisation, the anti2 conformation of the 1,5-hexadiene was drawn in GaussView 5.0.

The energy of the molecule was found to be -231.69253520 a.u. and the point group was determined to be Ci. The table from this section has been included below as it will be easier to refer to when comparing geometries below:

Structure	Calculation Summary	Point Group
		Ci

In this section, this molecule was re-optimised using Density Function Theory (DFT) and the 6-31G basis set, a higher level of theory.

The energy of the molecule was found to be -234.61171166 a.u. and the point group remained as Ci.

The table below shows the Jmol of the molecule and a summary of the results:

Structure	Calculation Summary	Point Group
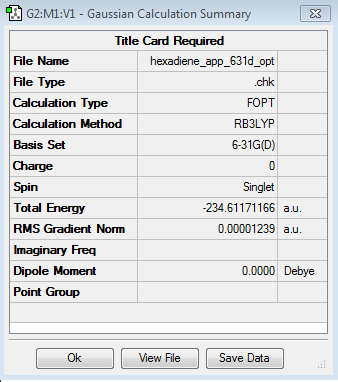
		Ci

Since two optimisations performed are at different levels of theory (HF/3-21 G and the DFT/6-31 G), it might not be that accurate to compare their values as the values are calculated in different ways.

Nonetheless, it is worth noting that relative energies (a.u.) of the HF/3-21 G and the DFT/6-31 G: -231.69253520 and -234.61171166 respectively, it can be seen that the energy difference between the structures is small. This small energy difference means that these structures can be found at the same point of the potential energy surface and are virtually the same. This idea is supported by the fact that the point groups do not change.

Comparing Geometries

Differences in carbon-carbon bond length and the angle between the carbon atoms exist between the optimised and re-optimised structures.

These differences can be seen in the table below. It is worth noting that the molecule has a centre of inversion and any changes in geometry will change on both sides of the centre inversion equally. Therefore only half the values for carbon-carbon bond length and carbon-carbon bond angles have been shown in the table. This also explains why the point group does not change and remains as Ci.

	carbon-carbon bond length (Å)			carbon-carbon bond angle (°)
	C1-C2	C2-C3	C3-C4	C1-C2-C3	C2-C3-C4	C1-C2-C3-C4	C2-C3-C4-C5
HF/3-21 G	1.31625	1.50896	1.55289	124.80847	111.35115	114.67416	179.99176
DFT/6-31 G	1.3350	1.50420	1.54816	125.29915	112.67064	118.58460	180.00000

The numbering of the carbon atoms can be related to the carbon atoms in the image below:

1,5-hexadiene Antiperiplanar conformer with numbered atoms

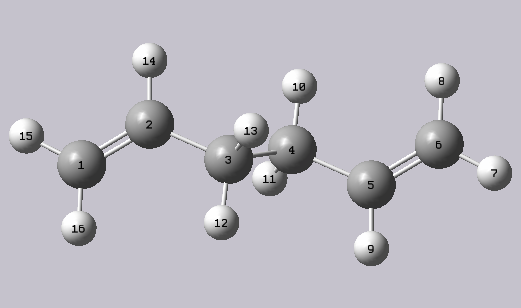
From the above table, several observations can be made: First of all, absolute values of the molecule's energies are incomparable, this is due to the fact that their approximations differ. The re-optimised DFT/6-31 G structure contains carbon-carbon bonds of greater length and larger carbon-carbon bond angles then the molecule at a lower level of theory.

Frequency Analysis at 298.15 K

Below is the data acquired from running a frequency calculation on the molecule of DFT/6-31 G level of theory.

Sum of electronic and zero-point Energies= -234.469215

Sum of electronic and thermal Energies= -234.461866

Sum of electronic and thermal Enthalpies= -234.460922

Sum of electronic and thermal Free Energies= -234.500800

The "electronic and zero-point" property, is the potential energy and is calculated at 0 K. The molecule is 'Frozen'.

The "electronic and thermal" properties are calculated at 298.15 K and 1.0000 atm. The energy is no longer 'frozen' and contains translational, rotational and vibrational contributions to the energy. As a result of this, the sum of electronic and thermal energy is higher than the sum of electronic and zero-point energy.

The electronic and thermal enthalpy can be calculated using the equation which assumes that the molecule behaves as an ideal gas:

H = E + RT

Where H = Thermal Enthalpy, E = Thermal Energy, R = The Ideal Gas Constant and T = Temperature (K)

Finally, the electronic and thermal free energy considers the entropy of the molecule, the equation includes the Gibbs free energy with a thermal correction and assumes constant pressure.

G = H - TS

Using the partition function of the molecule will allow the determination of the entropy of the system, which enables the use of the above equation. The partition function is not 0 at 298.15 K so higher levels can be accessed which contributes to energy Included in this equation is the equality: ΔPV = ΔNRT which corresponds to an increasing number of moles with as the reaction progresses.

A minimum can be calculated but so can a transition state, in order to determine what has been calculated, it is important to look at the IR spectrum. The IR spectrum is shown below in order to check that a minimum was in fact calculated and vibrations are correct:

IR spectrum: calculated frequencies for the 6-31 G antiperiplanar optimised 1,5-hexadiene

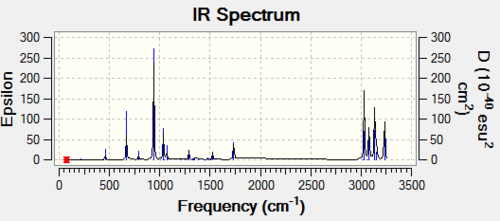
From the IR spectrum, it can be seen that all frequencies are positive, there is not an imaginary frequency. This means that the minimum was calculated and not the transition state. It is possible to determine the CH stretches associated with the peaks in the spectrum but these are not particularly of interest during frequency analysis. Instead, group theory is used to calculate intensities of hydrogens which are then expressed as a minimum.

Optimising the chair and boat transition structures

This section will address the chair and boat conformations. These are the conformations of the transition states of the cope rearrangement.

The cope rearrangement is a concerted reaction and goes through a cyclic transition state where a sigma bond is broken and simultaneously another sigma bond is formed. The chair and boat conformations are two possible conformations of this cyclic transition state.

Both the chair and boat conformations were optimised in this experiment, in addition, the reaction pathways were analysed and activation energies for both conformers were found using the Intrinsic Reaction Pathway (IRC).

By use of two HF/ 3-21 G allyl fragments, the chair transition state was constructed using GaussView 5.0. This was followed by a relaxation of the point group which enabled the distance between allyl end groups to be set to 2.2 Å. Subsequently, a variety of methods were used to optimise the structure.

Optimising the chair by calculating force constants

Using GaussView 5.0, a guess chair structure was optimised using an optimisation + frequency was run using HF/ 3-21 G and TS(Berny). The optimisation could potentially crash or fail if 2 or more imaginary frequencies were detected. The keyword opt=noeigen was used in the input line to prevent this. The force constants were calculated.

The energy of the molecule was found to be -231.61932245 and one imaginary frequency that results in the cope rearrangement was found at -817.87 cm-1.

The table below shows the Jmol of the molecule and the summary of the results:

Structure	Calculation Summary

negative frequency animation

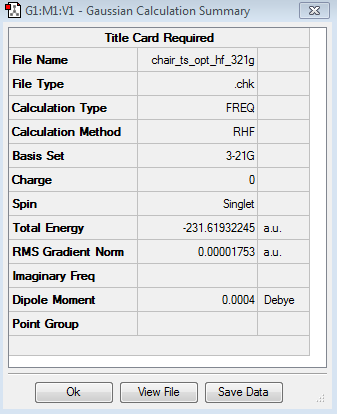
The minima in the PES represent the transition states and the second derivative of the PES is the force constant. This is then used in the quantum harmonic oscillator where it is square rooted to obtain a frequency.

The imaginary frequency

Rationalising the imaginary frequency:

1. $\frac{\partial E(x)}{\partial x}$

The first derivative of energy with respect to nuclear position.

2. $k=\frac{{\partial }^{2}E(x)}{\partial x^2}$

The second derivative is produced as this can determine whether a minimum or a transition state occurs. Lack of a negative value (only positive values) means a minimum has been found and thus the presence of one negative value means a transition state has been found. This second derivative is equal to the force constant $k$

3. $v=\frac{1}{2\pi }\sqrt{\frac{k}{\mu }}$

The equation above links $k$ , to the Harmonic Oscillator's vibrational frequency

Nf710 (talk) 15:47, 11 February 2016 (UTC) Very good use of equations to explain the force constants significance

Optimising the chair by the redundant coordinate editor

Using GaussView 5.0, a guess chair structure was optimised using HF/ 3-21 G. The keyword opt=modredundant was used in the input line as the redundant coordinate editor was used to freeze the distance between the allyl end groups.

In order to calculate the force constant for the simultaneous bond breaking and making process instead of for the whole molecule; the previously frozen bonds were set to 'Derivative' and then the molecule was re-optimised to TS (Berny).

The energy of the molecule was found to be -231.61932243 and one imaginary frequency was found at 817.84 cm-1. It can therefore be concluded that the molecule obtained corresponds to a transition state.

The table below shows the Jmol of the molecule and the summary of the results:

Structure	Calculation Summary

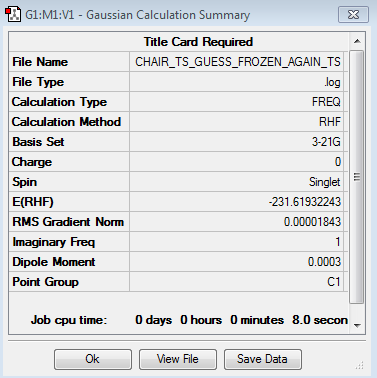
A comparison of the molecules is possible as they have both been optimised using the same HF/3-21 G basis set. A comparison of the two energy values obtained, the difference between them can be calculated to be a insignificant: 0.63 Jmol-1 . Allyl group distances (Å) only differed beyond the second decimal point. Both of these observations can lead to the conclusion that the first optimised structure was actually sufficient enough to lead to the desired transition state conformation, it is near enough to reality.

Optimising the boat by QST2 and QST3 methods

The first step of this process was to number the carbon and hydrogen atoms of both the reactant and the product structures of the reaction mechanism. This was done for both methods but, in addition, the QST3 method uses the transition state guess structure.

The anti2 product of the QST2 method was not as expected. To perform the calculation, the antiperiplanar conformation was used. The calculation ran but the resulting product does not make sense: its new bond length (Å) is far too long: 3.14665, the program simply translated one double bond on top of the other as it did not consider bond rotation.

Structure	Molecules with numbered atoms

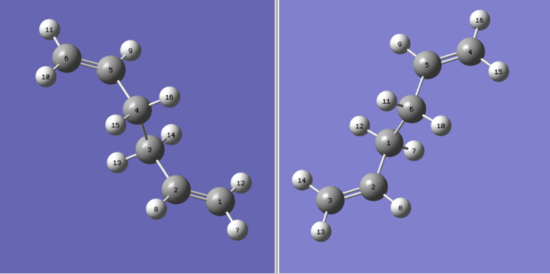To fix this problem, the molecules were arranged so that a more realistic reaction geometry was achieved. Both the reactant and product's central dihedral angles were changed to 0° and internal angles set to 100°.

Structure	Molecules with numbered atoms

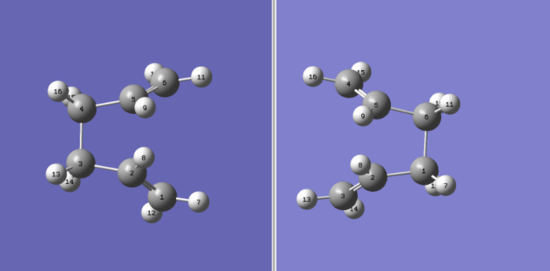The result of this optimization is a transition structure with an energy of -231.60280246 a.u. confirmed by imaginary frequency at -839.99 cm-1.

To perform the QST3 calculation, the antiperiplanar conformation and guess structure was used. The calculation ran but, as a result of a substantial difference in the initial and final structures, there was insufficient information to form the correct transition state. With this in mind, it was considered insufficient to alter the geometry of the reactants and products and the result from the QST2 calculation deemed as sufficient.

Running the Intrinsic Reaction Coordinate calculation (IRC)

Without further investigation, it is impossible to determine which of the two transition states through which a reaction would proceed. This cannot be done by just looking at the molecules, it is necessary to run an Intrinsic reaction coordinate to visualise the reaction's PES. In the IRC, the minimum energy path of the PES is obtained by creating multiple points by slightly changing the coordinates of the atoms; this will help to follow the minimum energy path from the transition structure to its local minimum down the steepest gradient.

The optimised boat transition structure was used in the IRC calculations, HF/ 3-21 G was used, force constants were computed at every step , the computation consisted of 50 steps and finally the computation was performed in the forward direction. The last constraint is selected as the cope rearrangement is symmetrical reaction with an identical reactant and product.

Below is a plot of the energy profile of the IRC and Animation of the transition state:

Animation of the transition state	IRC Plot

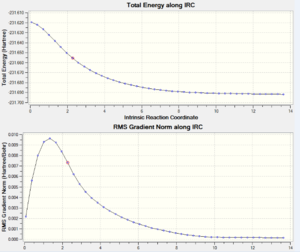Nf710 (talk) 15:52, 11 February 2016 (UTC) you could have worked this out bu optimizing down the final structure and comparing the geoms and energies This plot shows the reaction progressing from the transition state to the product (or the reactant). The minimum was found to be at step 45, because this is where the calculation ceased and there is a plateu of the graph.

The energy of the molecule was found to be -231.69160646

It is possible to check that the minimum is correct by:

1. Optimising the resulting molecule: The absence of an imaginary frequency confirmed the minimum.

2. Running a IRC with more steps: A 70 step IRC was run but it failed to offer a results any different from the calculation at 50 steps.

Overall, the correct minimum structure was generated and any additional optimisations would prove obsolete.

Analysing the activation energies of the chair and boat transition structures

Both structures were re-optimised using DFT/6-31 G, a higher level of theory.

The optimised chair transition state was of point group: C2h. The Optimisation log file can be found here

The optimised boat transition state was of point group: C2v. The Optimisation log file can be found here

Here is a table summarising the results C1-C1 is the distance between the terminal carbon atoms of both allyl fragments and C1-C2 is the distance between the adjacent carbons in the same allyl fragment

	chair (Å)		boat (Å)
	C1-C1	C1-C2	C1-C1	C1-C2
HF/3-21G and QST2 respectively	2.02034	1.38925	2.13997	1.38148
DFT/6-31G	1.96712	1.40756	2.13997	1.38148

According to the table above, there is an insignificant difference between the bond lengths between the two levels of theory. There is no change in the point group either.

	HF/3-21G			DFT/6-31G
	Electronic energy	Sum of electronic and zero-point energies at 0 K	Sum of electronic and thermal energies at 298.15 K	Electronic energy	Sum of electronic and zero-point energies at 0 K	Sum of electronic and thermal energies at 298.15 K
Chair transition state	-231.61932230	-231.46670541	-231.46134598	-234.55698376	-234.41492954	-234.40900899
Boat transition state	-231.60280252	-231.45092212	-231.44529401	-234.54309342	-231.450930	-234.39600734
reactant: anti2	-231.69253522	-231.53954032	-231.53256610	-234.61171035	-234.46920482	-231.46185716

Due to the insignificant difference in bond lengths between the two levels of theory, analysis of the activation energies is necessary.

The activation energy was calculated by taking the difference between reactant relative energies and the energy of the transition states (from the table above)

At 0 K the activation energy is calculated by using the sums of electronic and zero-point energies (to incorporate vibrational and rotational energies). At 298.15 K the activation energy is calculated by using the sums of electronic and thermal energies.

The table of results below shows that, in both levels of theory, the chair transition state has a lower activation energy for both levels of theory. Therefore it can be concluded that the reaction will proceed through the the chair transition state.

There is a large difference between the activation energies for both transition structures between the levels of theory.

According to the literature, the activation energy at room temperature for boat and chair transition structures are 140 kJmol-1 and 187 kJmol-1 respectively. These values are closer to the higher level of theory (DFT/6-31G method) which proves more accurate .

	HF/3-21G		DFT/6-31G
	0 K	298.15 K	0 K	298.15 K
Chair TS (kJmol-1)	191.2207727	186.981303	142.495643	138.751212
Boat TS (kJmol-1)	232.6582223	229.1241451	175.5405975	172.8857432

Nf710 (talk) 15:55, 11 February 2016 (UTC) your enehgies are correct and you have come to the conclusion that lower basis sets can approximate the geometries quite well. but not energies. In general this was a good report and you have done everything asked of you however you could have gone into more detail on the theory about the various methods.

Diels Alder Cycloaddition Exercise

Introduction

Another example of a concerted pericyclic organic reaction is the Diels-Alder cycloaddition. It is a [4+2] cycloaddition between a conjugated diene (4 π electron unit) with a substituted alkene or dienophile (2 π electron unit). The net output of this type of reaction is the breakage of σ C-C single bonds, this provides a thermodynamic driving force for this process. This is a result of the fact that the energy cost of breaking two π bonds is lower than the energy released by the formation of σ bonds i.e. σ are stronger than π bonds . This reaction requires thermal activation at room temperature which leads to a significant increase in yield. The reaction proceeds via simultaneous and concerted bond making and breaking and a cyclic transition state.

(You mean "The net output of this type of reaction is the breakage of 2 π C-C bonds and the formation of two σ C-C single bonds"? Tam10 (talk) 13:43, 11 February 2016 (UTC))

Diels-Alder Cycloaddition reaction scheme

Diels-Alder reaction can be set up either as normal or inverse electron demand, depending on the reactant’s substituents. The normal electron demand consists of the dienophile with an electron withdrawing group (producing the LUMO) interacting with a diene with an electron withdrawing group (producing the HOMO). This strong interaction between the two interacting orbitals is a result of a small energy gap between them. On the other hand, the inverse electron demand consists of the interaction between the LUMO of the diene and the HOMO of the dienophile. In this case, the dienophile contains the electron donating group and the diene contains the electron withdrawing group. In this section, the reaction between cis-butadiene with ethane will be discussed. The next section will discuss the reaction between Cyclohexa-1,3-diene (conjugated diene) and maleic anhydride (substituted alkene). The former is symmetrical and the latter is unsymmetrical. In order to study the selectivity and symmetry of these reactions, their transition states will be optimised and their LUMO and HOMO will be analysed.

Reacting ethane with cis-butadiene

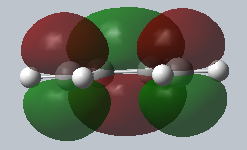
Labelled cartesian axes	HOMO of cis butadiene	LUMO of cis butadiene

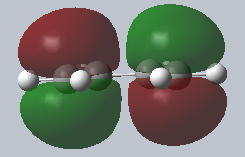The molecules of cis-butadiene and ethene were draw in GaussView 5.0, both molecules were subsequently optimised using the Semi-Empirical AM1 method. This method is much faster than the method it originates from, Hartree-Fock. The reason for this is the fact that the method excludes some of integrals and involves the Zero-Differential Overlap Approximation. A downside is: if the drawn molecule fails to resemble molecules stored in the database, the computation itself will fail. The cis-butadiene’s dihedral angle is altered to 0.00° and then symmetrised to the C2v point group. The images above show that, with respect to the Cartesian coordinates’ yz plane; the LUMO is symmetric and the HOMO, asymmetric.

Transition state optimisation

The optimised cis-butadiene molecule and the optimised ethene molecule were combined and optimised to generate a transition structure. For this optimisation, the molecules were set to be 2.2 Å apart and optimisation to a TS (Berny) using the semi empirical AM1 method was used. In addition, the coordinates were frozen and point group set to be Cs. Following this, a subsequent optimisation was performed to a TS (Berny) and using the redundant coordinate editor. An imaginary frequency at -956.14 cm-1 confirmed the presence of the transition state: it shows the reaction path at the transition state (bond formation) with energy 0.11165475 a.u. This imaginary frequency is shown below as synchronous and the lowest positive frequency at 147.54 cm-1 is also shown as an asynchronous rocking.

(Did you forget to put these animations in? File:-956vibration_jp1713.gif File:Highestvibration_jp1713.gif Tam10 (talk) 13:43, 11 February 2016 (UTC))

Structure	Calculation Summary
Diels Alder Transition State

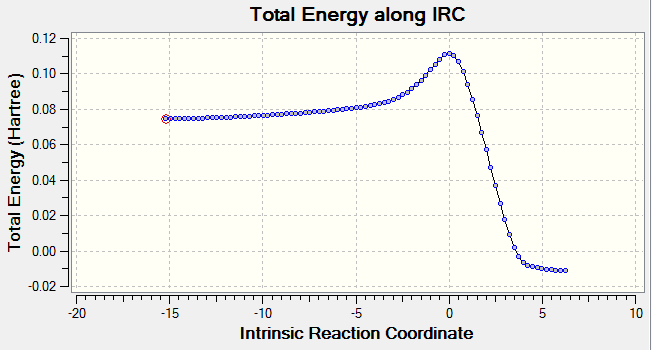
Running the Intrinsic Reaction Coordinate Calculation (IRC)

It was necessary to run an IRC on the transition state structure with 100 steps, the minimum of the reactants was found at step 62. The plot below shows the IRC with the reactants on the left hand side and the products on the right hand side. It can be observed from this plot that product has much lower energy then the reactants; the reaction is Exothermic. I also can be observed that there is no sign of any other transition state structures or intermediates between the reactants and the products. The reason for this observation is the absence of the IRC stopping at a minimum point that corresponds to the intermediate. Finally, it can be seen that the energy of the transition state is very close to that of the reactants. According to Hammond’s Postulate, this transition state is ‘early’.

Animation of the transition state	IRC Plot

The bond lengths in the envelope transition state structure were investigated and shown in the table below (the carbon numbers refer to the numbered carbons on the diagram below). The partially formed σ bonds were found to be 2.1194 Å, it can be said, from this, that this is not a single bond but the there is certainly a bonding interaction present. This conclusion can be supported by the fact that these bonds are within the van der Waals radius of two carbon atoms (3.4 Å) but much longer than sp2 (1.54 Å) and sp3 (1.34 Å) hybridised carbon bond lengths.

Transition state, numbered atoms

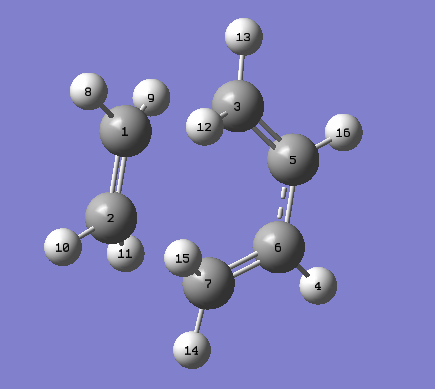
C1-C2 (Å)	C1-C3 (Å)	C2-C7 (Å)	C3-C5 (Å)	C5-C6 (Å)	C6-C7 (Å)
1.38301	2.11935	2.11936	1.38187	1.39749	1.38188

Reactant MOs: HOMO and LUMO

Ethene	Cis-butadiene	Transition Structure
Symmetric (HOMO) Antisymmetric (LUMO)	Antisymmetric (HOMO) Symmetric (LUMO)	Antisymmetric (HOMO) Symmetric (LUMO)

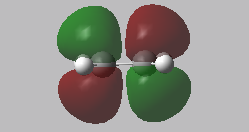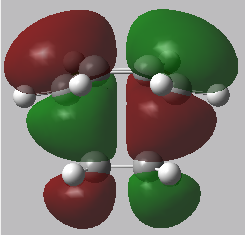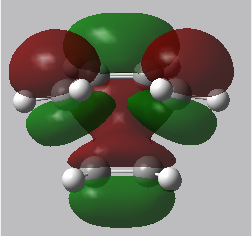(The images for butadiene appear to be the wrong way around Tam10 (talk) 13:43, 11 February 2016 (UTC))

In the transition state, the stability of the molecule is maximised by high orbital overlap and therefore an increase in stereoelectronic effects. Orbital analysis is necessary at this point. As described in the introduction section, the orbitals that interact to form the bonding MO are the LUMO of the dienophile and the HOMO of the diene.

From the energies below it can be seen that the HOMO of the diene is lower than that of the dienophile so therefore this forms the symmetric HOMO of the transition state. The asymmetric LOMO of the transition state is therefore formed using the LUMO of the diene and the HOMO of the transition state. The Woodward Hoffmann rules (preservation of the orbital symmetries during a pericyclic reaction) can be used to rationalise this, the reaction follows a normal electron demand.

The Woodward Hoffman Rules:

Allowed reactions involve the interaction of the HOMO of one reactant with the LUMO of the other reactant. If the reactants are more symmetrically similar, significant orbital overlap between these two orbitals will occur.

Energies:

	Ethene	Butadiene	Transition state
LUMO	asymmetric 0.05284a.u.	symmetric 0.01707 a.u.	symmetric 0.02314 a.u.
HOMO	symmetric -0.38777 a.u.	asymmetric -0.34381 a.u.	asymmetric -0.32392 a.u.

Reacting cyclohexa-1,3-diene with maleic anhydride

A classical example of the Diels-Alder reaction is the cycloaddition between cyclohexa-1,3-diene with maleic anhydride. The regioselectivity of this reaction (normal electron demand) can be investigated using GaussView 5.0.

The energy of the dienophile is lowered as electron withdrawing carbonyl groups on the maleic anhydride dienophile make it very electron poor. On the other hand, the diene, cyclohexa-1,3-diene is the electron rich molecule. The major interaction of this reaction is between the LUMO of maleic anhydride and the HOMO of cyclohexa-1,3-diene

Assuming the cyclohexa-1,3-diene is fixed in space; The asymmetric nature of this reaction (the reaction in the previous section was symmetric) means that there are two possible reaction approach trajectories. These can result in two geometrically different transition states: endo- and exo-.

In order to determine a preferred reaction pathway, relative energies of the MO's of the transition state structures were investigated.

In order to do this, the Semi-empirical AM1 method was used to make a guess structure. By changing the orientation of the cyclohexa-1,3-diene by 180°, it was possible to create two different approach trajectories. Distance between the molecules were set to 2.2 Å. This was then optimised (and a frequency calculation) to a TS(berny) using a semi-empirical AM1 method.

A transition state was confirmed by generating an IRC path and a negative frequency at 811.31 cm-1.

Exo transition state

Initial optimisation of the exo transition state was performed. A negative frequency at -812.20 cm-1 and energy of -0.05041985 a.u. confirmed the presence of a transition state and the concerted mechanism of the reaction. Syn addition of new bonds is also observed. The imaginary frequency was obtained by running an IRC of the reaction using the semi empirical AM1 method. The IRC graph is reversed as it corresponds to the backwards reaction (products of the diels alder on the left and reactants on the right).

Animation of the imaginary vibration	Summary

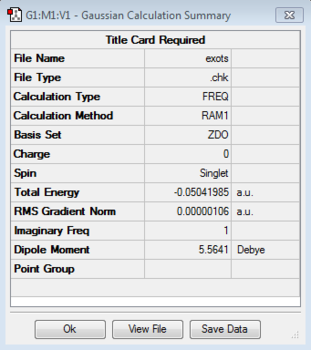Animation of the transition state	IRC Plot (Backward)

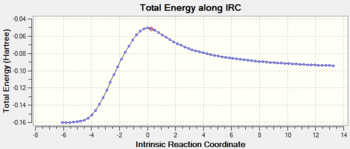Analysis of the bond lengths in this structure is necessary to examine the nature of bonding and geometry of this transition state structure. The table below summarises the bond lengths (the numbered carbons refer to the image of the transition state below).

The bonds formed between the molecules in the process described in the previous section (cis-butadiene and ethene) were of length 2.119 Å, this is a similar length to the bonds formed in this process (C2-C7 & C3-C9) 2.170 Å. Once again it can be said that the bonds are within the van der Waals radius of two carbon atoms (3.4 Å) but much longer than sp2 (1.54 Å) and sp3 (1.34 Å) hybridised carbon bond lengths. This confirms the presence of a favourable electronic interaction but not necessarily a single bond. Within the ring, the carbon bond lengths are all similar to that of carbon-carbon single bond and double bond distances which suggests delocalisation of electrons.

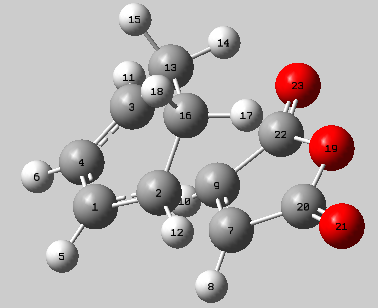
Exo transition state
C2-C7	C1-C4	C1-C2	C7-C9
2.17039	1.39676	1.39438	1.41011

Endo transition state

The same approach was used to optimise the endo structure as the exo structure. The only difference between the two processes is the orientation of the approaching cyclohexa-1,3-diene molecule (the carbonyl groups of the maleic anhyrdie are below the double conds of the cyclohexa-1,3-diene ).

A negative frequency at -806.32cm-1 and energy of the optimisation -0.05150479 a.u. confirmed the presence of a transition state and the concerted mechanism of the reaction. The imaginary frequency was obtained by running an IRC of the reaction using the semi empirical AM1 method. The IRC graph corresponds to the forwards reaction (reactants of the diels alder on the left and products on the right).

Animation of the imaginary vibration	Summary

Animation of the transition state	IRC Plot (Forward)

Analysis of bond lengths is similar to that of the exo transition state. A favourable electronic interaction is observed between C1-C7 and C4-C9 for the same reasons as in the endo transition state. The bonds in the ring hava a similar length to carbon-carbon single bond (1.54 Å) and double bond distances (1.34 Å) which suggests delocalisation of electrons.

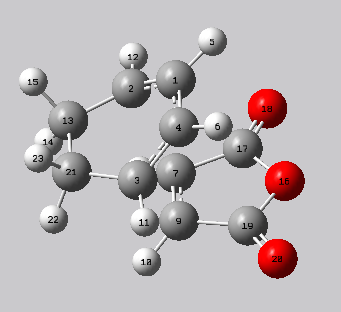
Exo transition state
C3-C9	C1-C4	C1-C2	C7-C9
2.16242	1.39725	1.39305	1.40847

Activation energy and geometry

The activation energies for both exo and endo structures were investigated in order to determine the preferred product of the Diels-Alder reaction.

The table below below shows the energies of the reactants and the products (units in a.u.):

maleic anhydride	cyclohexa-1,3-diene	sum of reagents	exo TS	endo TS	ΔEexo	ΔEendo
-0.12182419	0.02795811	-0.09386608	-0.05041985	-0.05150479	0.04344623	0.04236129

(From the energy of cyclohexadiene that you have, I can tell you're not using the geometry optimised structure in your calculations. Gaussian probably got stuck on the symmetric structure that you have, which is actually a TS joining two mirror images. If you perform a frequency analysis on this structure you'll see this imaginary frequency Tam10 (talk) 16:08, 11 February 2016 (UTC))

It can be seen from the table that there is a substantial difference between the activation energy of the endo transition state and the exo transition state (0.00108494 a.u.) from this it is possible to conclude that the endo transition state is the kinetically favoured product due to its lower activation energy.

It can been seen that the energy of the endo product is also the thermodynamically favoured product as the energy is lower than the exo. This can further be explained by looking at the geometries.

The images below aid the understanding of the relative energies of the exo and endo transition states. The distances between the carbonyl oxygen atoms in the maleic anhydride and the hydrogen atom in the cyclohexa-1,3-diene can be compared. In the exo it is around 2.693 ‎Å and endo it is longer 3.317 ‎Å. A shorter distance (in this case, exo) would be less energetically favourable as there would be a steric clash between the atoms leading to a more strained molecule. (van der waal radi of hydrogen and oxygen combined is 2.70 ‎Å)

Endo transition state	Exo transition state

Reactant MOs: Secondary orbital overlap

The images below show the orbitals of the transition states, these are used to investigate the electronic interactions. It can be seen that the HOMOs and LUMOs of the exo and endo transition states are all antisymmetric. It can also be seen that the there is a difference in the nodal planes between the HOMO and the LUMO. In the HOMO, the nodal planes pass only through the atoms (energetically unfavourable). The LUMO has another nodal plane that lies between the two approaching reagents. This shows the presence of excited states. The Jmols of the MOs can be seen in the link here

It is particularly useful to look at these interactive jmols of MOs when considering secondary orbital overlap.

Exo transition state

The orbital images in the link demonstrate that only primary orbital interactions exist and there is a lack of secondary orbital interactions. It can be seen that the distance between the π C=C orbitals on cyclohexa-1,3-diene and the π* C=O orbitals on the maleic anhydride is too great to interact as the molecules approach each other.

Endo transition state

Upon looking at the images of the orbitals LUMO +1 and LUMO +2, it can be seen that there is a significant orbital overlap between the π C=C orbitals on cyclohexa-1,3-diene and the π* C=O orbitals on the maleic anhydride. This confirms the presence of a secondary orbital overlap and the delocalisation of electrons leads to a decrease in the overall energy of the transition state structure. As a result the endo product is more kinetically favourable.

Conclusion

This experiment has successfully studied three pericyclic reactions.

The Cope rearrangement of 1,5- hexadiene was successfully studied in the tutorial section.

It was found that this reaction proceeds through the chair transition state structure due to it being lower in energy than the boat transition state structure. This is the kinetic pathway of the reaction.

The gauche3 structure was found to be the lowest energy conformer of the reaction. This was justified by using the idea of orbital overlap. The π orbitals of the terminal C=C double bonds overlap very favourably.

This reaction was optimised using HF/3-21 G and also a higher level of theory, DFT/6-31 G. By looking at the very similar geometries, bond lengths and point groups of the optimised structures, it is not possible to rationalise the preferred transition state.

It was necessary to look at the activation energy and IRC of these structures, from which the preferred pathway was determined to be the chair transition state. The activation energies at room temperature for the chair transition state was found to be closer to the literature values.

Both the Diels-Alder reactions of cis-butadiene and ethene and then cyclohexa-1,3-diene were successfully studied in the exercise section.

The transition states for both of these more complex reactions were computed using the semi-empirical AM1 method. This method was chosen as it is much faster than the HF/3-21G and DFT/6-31G methods but it also has a lower degree of accuracy.

Transition states were always confirmed by the presence of one imaginary frequency.

It was found that the C-C bonds formed between the reacting molecules involve a favourable interaction but longer than a single C-C bond. Van der waals radii were used to rationalise these results.

Preservation of the MO symmetries in this reaction also support the fact that the reaction occurs successfully.

The Diels-Alder cycloaddition between cyclohexa-1,3-diene and maleic anhydride was studied to investigate selectivity of these reactions. It was found that the endo product is favoured both thermodynamically and kinetically due to the fact that it has lower energy and activation energy respectively than the exo transition state.

This is justified by the secondary orbital interaction present in the endo product which is absent in the exo. There is also significant steric strain in the exo structure. this was also rationalised using the van der walls radii.

There are two noticeable flaws in the computational methods. Firstly, the calculations neglect intermolecular reactions as only one molecule has been considered so far and treated as an ideal gas. A failure to consider intramolecular interactions could lead to computation of incorrect energy values. Secondly, it is not possible to optimise a transition state from a guess structure for a unknown reaction. It was possible in the case of these exercises as the transition structure is known and can be replicated easily.

Future work can include studying the effect of increasing steric strain on the Diels-Alder reactions. This can be done by using more substituted reagents.

References

References are the in RSC format.

<references>