User:Jk2510

Introduction

Two examples of cyclic reactions were studied - Cope rearrangement and Diels Alder cycloaddtion. For each reaction, two possible structures of transition states were identified from literature. Using computational methods, the energy, geometry and the thermochemical data were calculated in order to investigate which reaction pathway is preferred.

The Cope Rearrangement

---

Optimization of Reactants and Products

Optimization of 1,5-hexadiene with an "anti" central linkage

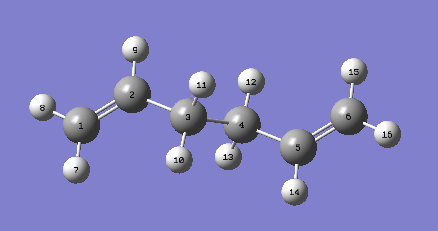
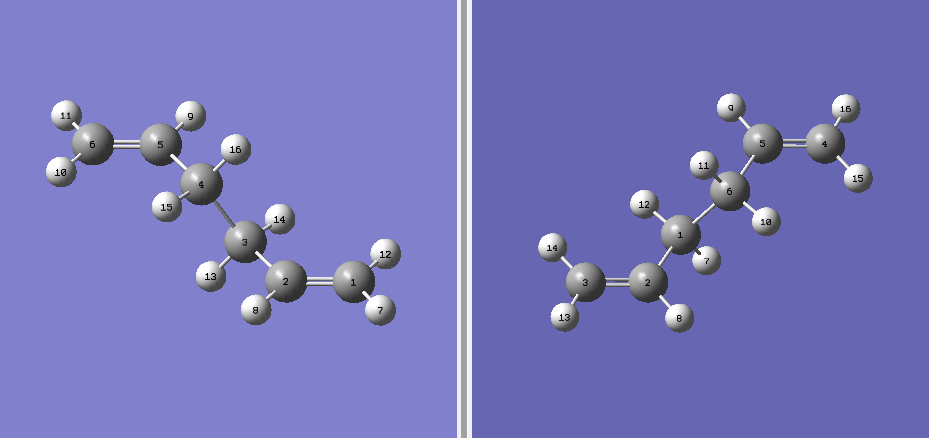
A 1,5-hexadiene molecule was drawn using Gaussview and was modified to have the central four carbon atoms at an antiperiplanar conformation. Then the molecule was optimized at the HF/3-21G level of theory. The point group of the molecule was found to be c_i. The molecular model diagram of the conformer is found on this link "Anti 2".

From the ten conformers of 1,5-hexadiene, the molecule drawn was identified as the anti2 conformer as shown in Figure X. A few more conformers were drawn and optimized with their energies compared as shown in Figure Y. It is expected for the gauche conformer to be in higher energy than the anti conformer, similar to the energy profile of simple linear molecules.

Name of Conformer	Energy HF/3-21G	Point group	Structure
anti2	-231.692535	Ci
gauche	-231.687716	C2

Figure 1. A table showing examples of conformations of 1,5-hexadiene.

Optimization of 1,5-hexadiene with a "gauche" central linkage

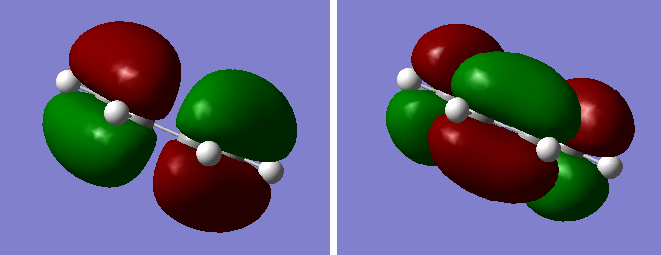
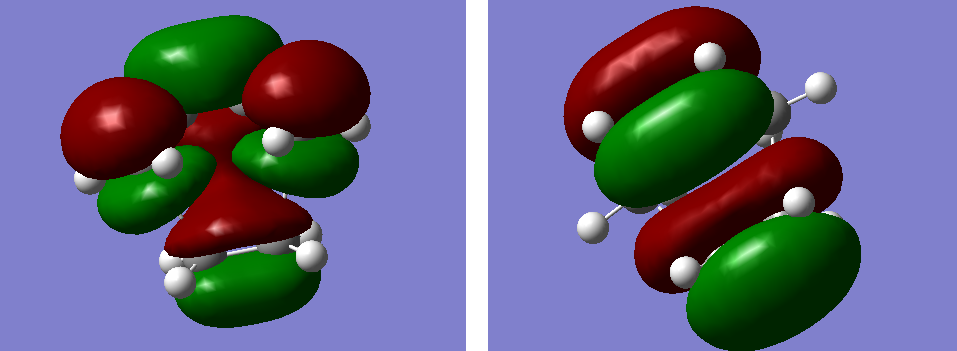
Another molecule of 1,5-hexadiene was drawn with a "gauche" linkage and then optimized using the same HF/3-21G level of theory.The structure in 3D is shown in this link, "Gauche". The point group of the molecule was c2. The energy of the molecule is higher than the anti conformer but the difference is not as large as the n-butane molecule (approximately 3.4kcal/mol). This means that there are other factors affecting energy of the molecules. From the previous studies of 1,5-hexadiene "Gung", it was observed that molecular orbital overlap can affect the overall energy of the molecule. By observing the molecular orbital models using Gaussview, we find that they could be possible stabilization of energy for gauche conformer due to overlap of π-electrons which is not possible in the anti-linkage. This is shown in Figure Z.

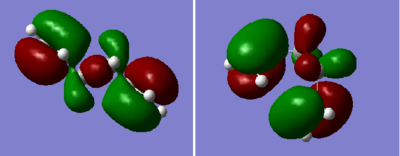
Figure 2. A diagram showing the MOs of anti-linkage(left), and gauche(right) conformer of 1,5-hexadiene. We see that it is difficult for anti-linkage to show any Π-cloud overlap.

Reoptimization of anti conformer

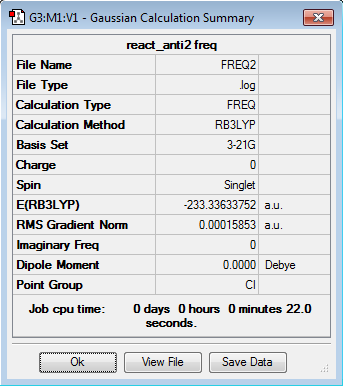
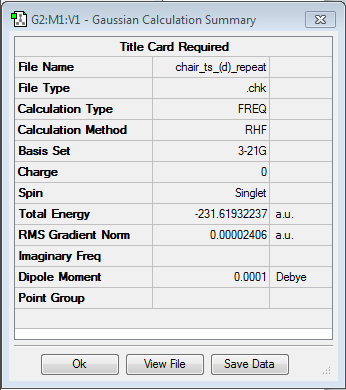
The anti2 conformer is the reactant molecule for the Cope arrangement. It was reoptimized using the B3LYP/6-31G* level of theory. This gave the following results as shown in Figure X:

Figure 3. A digram showing the summary of results from the reoptimised anti2 conformer.

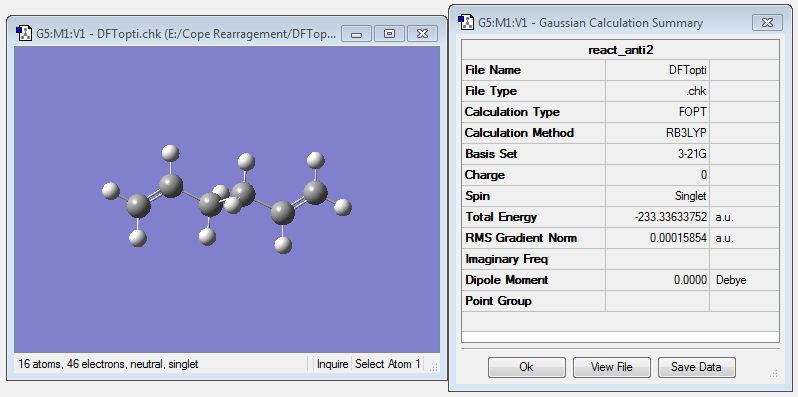
It is shown that the value of the gradient is lower than 0.001, so the optimization is complete. The final energy of the reoptimised conformer is much lower than the energy optimized at the level of HF/3-21G theory. The difference is energy is 1.64238 a.u. or approximatley 1031.5 kcal/mol.

Conformer	Energy HF/3-21G	Energy B3LYP/6-31G*
anti2	-231.69254	-233.33634

The structures of the conformers from the two optimizations appear to be very similar. To see if the change in geometry has any link with the decrease in energy, the structure was investigated in more detail. The C-C bond lengths and dihedral angles of the terminal four carbons were compared.

Figure 4. A digram of anti2 conformer with labelled carbon atoms

C-C bond type	Bond length B3LYP/6-31G*	Bond length HF/3-21G
C1=C2, C5=C6	1.3161	1.3316
C2-C3, C4-C5	1.5089	1.5113
C3-C4	1.5528	1.5609

Figure 5. A table comparing the carbon-carbon bond lengths of the different optimizations

C-C bond type	Bond angle B3LYP/6-31G*/°	Bond angle HF/3-21G/°
C1=C2-C3-C4, C3-C4-C5=C6	118.67	114.61
C2-C3-C4-C5	180	180

Figure 6. A table comparing the dihedral angle of the molelcule from two different optimizations

When comparing the geometries of the two differently optimised conformers, there is a slight decrease in bond length and an increase in dihedral angle. The increase in dihedral angle may position the C-H and C-C bonds so that the orbitals are in better overlap of each other, hence the overall decrease in energy of the molecule. The better overlap of orbitals also result in a decrease in bond length between the carbon atoms.

Frequency Analysis of the Reoptimized anti-linkage conformer

From the B3LYP/6-31G* structure, a frequency calculation was done. The results gave a value of energy equal to the value from the previous optimization, -233.3363 a.u., which shows that the structure is correct.

Figure 7. A table showing the energy of anti2 conformer from the frquency calculation.

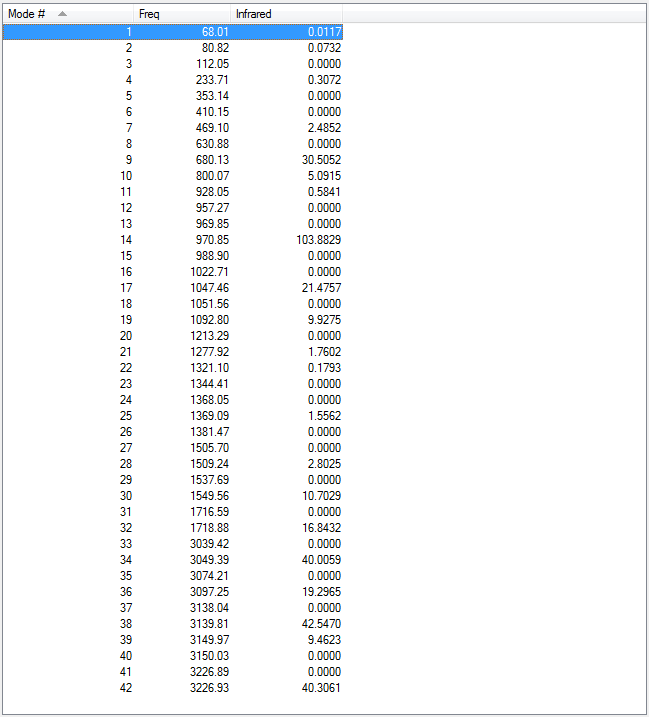
A list of all the vibrational frequencies was obtained from the frequency calculation of the reoptimized species. The results showed that all the frequencies were positive. This meant that all the values were real and from these values an infrared spectrum was simulated.

Figure 8. A table showing the values of vibrational frequencies of reoptimised anti2 conformer.

Figure 9. A simulated IR spectrum of B3LYP/6-31G8 optimised anti2 conformer.

Figure 9 shows that all the vibrational frequencies give zero intensity in IR absorption, so would not be seen in an actual IR spectrum. This is because the vibrational modes of the molecule are IR inactive, there is no dipole moment in the molecule. This is also evident in the summary of results (Figure 7), where the dipole moment is 0.00 Debye.

Thermochemistry

The thermochemistry data were also collected from the frequency calculation:

Temperature (K)	Sum of electronic and zero-point Energies (a.u.)	Sum of electronic and thermal Energies (a.u.)	Sum of electronic and thermal Enthalpies (a.u.)	Sum of electronic and thermal Free Energies (a.u.)
298.15	-233.192876	-233.185576	-233.184632	-233.224526

Figure 10. A table showing the sum of different energies and enthalpies from B3LYP/6-31G* structure

Optimization of the "Chair" and "Boat" Transition Structures

Allyl Fragments as Building Blocks

The two transition structures for the Cope arrangement were identified as "chair" and "boat" structures.

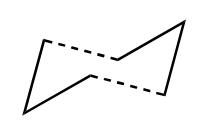
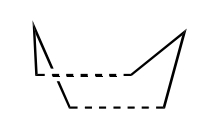A digram showing the chair(left) and boat(right) TS structures.

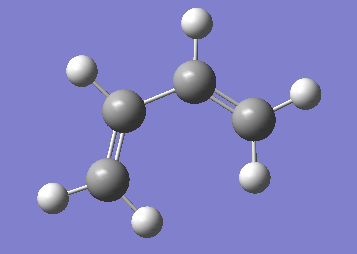
An allyl fragment was drawn and optimized - this was used as the building block of the two transition states (click here for optimized file).

Figure 11. A digram showing the structure of the allyl molecule.

Then the structure of transition states were modelled by aligning two allyl fragments with a distance of 2.2 Å. One set was constructed to have an approximate chair conformation and was optimized to a TS(Berny). The point group of the molecule was C2h. The output file gave following results:

Figure 12. An animated video of the vibration modes from the HF/3-21G level optimization to a TS(Berny).

The frequency calculation gave one imaginary frequency of 818.24cm^-1.

Vibration mode animation is shown in Figure 12. - one pair of terminal carbon atoms move away fro each other while the other pair comes closer and forms a bond. This is in synchronized motion and represents the one in the Cope arrangement.

Thermochemistry

Temperature (K)	Sum of electronic and zero-point Energies (a.u.)	Sum of electronic and thermal Energies (a.u.)	Sum of electronic and thermal Enthalpies (a.u.)	Sum of electronic and thermal Free Energies (a.u.)
298.15	-233.466692	-233.461335	-233.460391	-233.494541

Figure 13. A table showing the sum of different energies and enthalpies from HF/3-21G optimized structure

Figure 14. A table showing the summary of results from HF/3-21G optimized structure

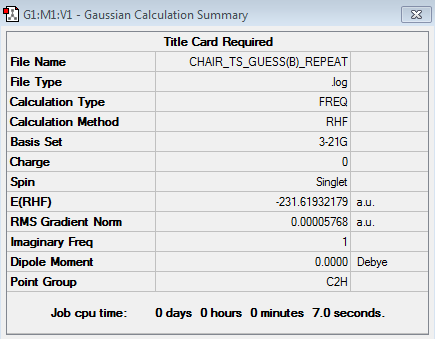
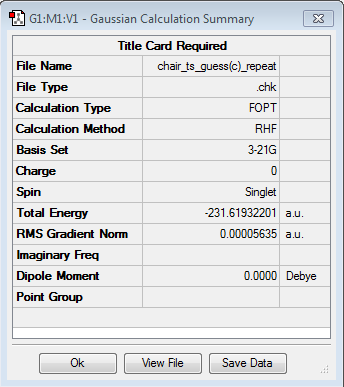
Reoptimization of the "Chair" using the Frozen Coordinate Method

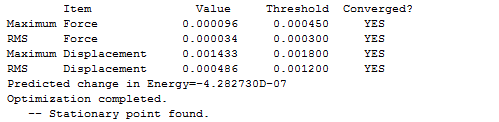
The Frozen Coordinate Method is another way of optimizing the molecule and produces better result. The bond that is broken and formed between the terminal carbons are fixed to a distance of 2.2 Å. The optimization at HF/3-21G level of theory gave following results:

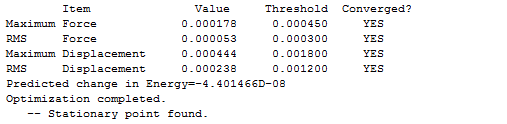
Figure 15. Evidence to confirm the success of optimization using the Frozen Coordinate Method.

The results show convergence on both values of force constants and displacement. Also, the energy of the molecule is -233.619 a.u. and the point group of the molecule is C2h, indicating that it has formed a "chair" structure.

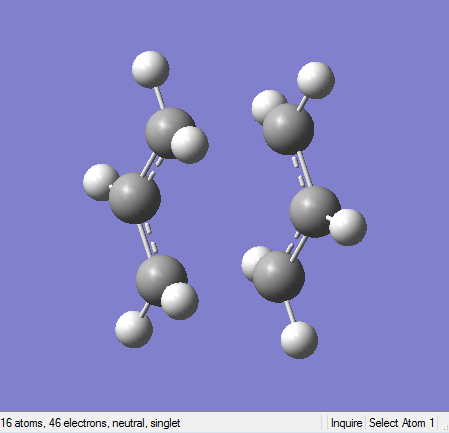
Figure 16. A diagram showing the optimised "chair" TS structure with frozen coordinates.

Reoptimization of the "Chair" using Unfrozen Coordinates

The reoptimized structure looks very similar to the first HF/3-21G optimized chair structure. Here, the redundant coordinate editor was used to find out about the two coordinates that being differentiated. The bond lengths of the terminal carbons that break/form were compared.

Bond length of HF/3-21G optimized structure (b) /Å	Bond length of reoptimized structure (d) /Å
2.0212	2.0192

Figure 17. A table comparing the bond distances of terminal carbons of two different optimizations.

The bond forming/breaking distance between terminal carbons of the transition state from (d) is lower than the structure from (b). This shows using the force constants give a slightly higher bond lengths than using the redundant coordinate editor.

Figure 18.An animated video of the reoptimized strucure.

The structure also shows similarities with (b) - there is only one imaginary frequency with value 818 cm^-1 .

Figure 19.An IR spectrum of the reoptimized strucure.

Figure 20.Evidence to show the success of the reoptimized strucure.

Optimization of the "Boat" using QST2 method

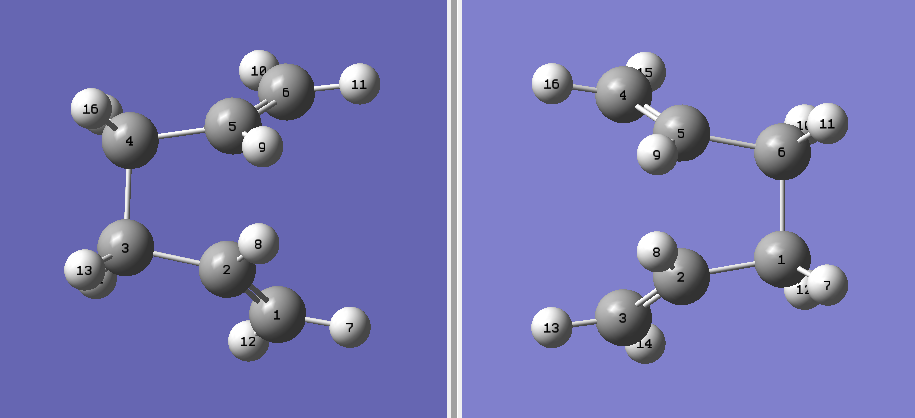
To optimize the "boat" structure, one molecule of 1,5-hexdiene was used as a reactant and product. The numbering of the product molecule was changed so that that it gives the numbering obtained after the rearrangement of the reactant molecule.

Figure 21.A diagram showing the arrangement and numbering of carbon atoms of reactant(left) and product(right).

The above optimization had failed and the correct "boat" structure was not shown using the QST2 method. Therefore, the 1,5-hexadiene molecule was rearranged as shown below and optimized.

Figure 22.A diagram showing the arrangement and numbering of carbon atoms of the modified structure of reactant(left) and product(right).

The optimization was successful after the modification. Both the values of force constants and displacement had converge and the point group of the molecule was C2v, indicating that we have the correct structure.

Figure 23. An animated video of the "boat" transition state structure.

Thermochemsitry

Temperature (K)	Sum of electronic and zero-point Energies (a.u.)	Sum of electronic and thermal Energies (a.u.)	Sum of electronic and thermal Enthalpies (a.u.)	Sum of electronic and thermal Free Energies (a.u.)
298.15	-233.450926	-233.445298	-233.444353	-233.479116

The Diels Alder Cyloaddition

Reaction between ethylene and cis-butadiene

Optimization of cis-butadiene

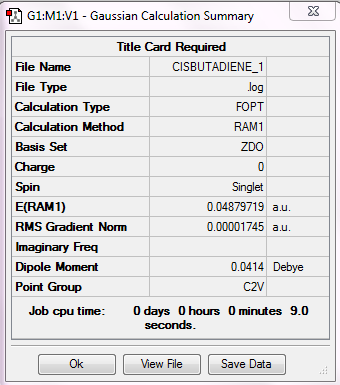
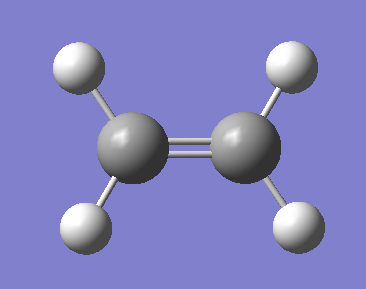
The Diels-Alder cycloaddition is a reaction between cis-butadiene and ethylene. First, a molecule was cis-butadiene was drawn and optimized using AM1 method.

Figure 24. A diagram showing the optimized molecule of cis-butadiene

HOMO and LUMO of cis-butadiene

From the optimization, a model of HOMO and LUMO was plotted. The symmetry of the two orbitals were found with respect to the plane of the molecule.

Figure 25. A diagram showing the unsymmetrical HOMO(left) and symmetrical LUMO(right) of the optimized cis-butadiene.

The molecular orbital diagram showed that the HOMO is unsymmetrical with respect to the plane of the molecule and the LUMO is symmetrical. These orbitals are involved in interaction with the orbitals ethylene.

Figure 26. Evidence to show that optimization was a success for cis-butadiene.

Both the force constant and displacement show convergence to zero and the gradient is less than 0.001. This means the optimization is successfully completed.

Temperature (K)	Energy (a.u.)/AM1	Point group
298.15	0.048797	C2v

Figure 27. A table showing the point group and energy of cis-butadiene.

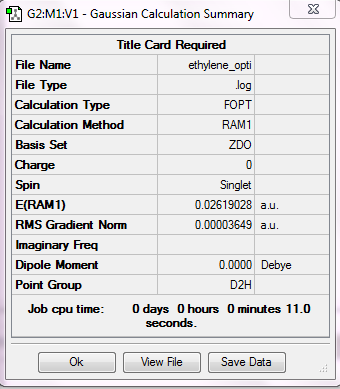
Optimization of ethylene

A molecule of ethylene was drawn and optimized using AM1 methods.

Figure 28. A digram showing the structure of optimized ethylene.

Figure 29. Evidence to show that optimization was a success for ethylene.

Both the force constant and displacement show convergence to zero and the gradient is less than 0.001. This means the optimization is successfully completed.

Temperature (K)	Energy (a.u.)/AM1	Point group
298.15	0.026190	D2h

The molecule shows a D2h point group, which shows that the structure is correct.

Optimization of the Transition Structure

The molecule of ethylene and cis-butadiene was aligned in a position where the bond breaking/forming distance is 2.1 Å (the van der Waals radius of the carbon atom is approximately 1.7 Å. ).This was the structure of the transition state.Then the structure was optimizes using semi-empirical AM1 method. Then the Frozen Coordinate method was used to reoptimize the structure. An imaginary IR frequency of 806 cm^-1 was obtained.

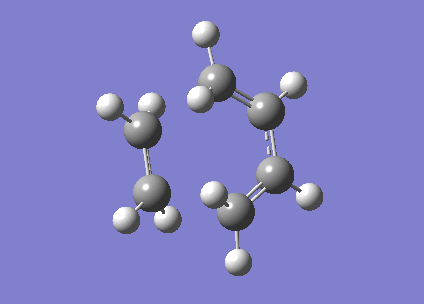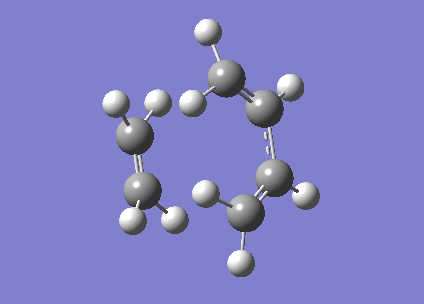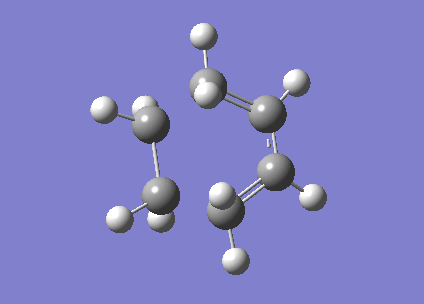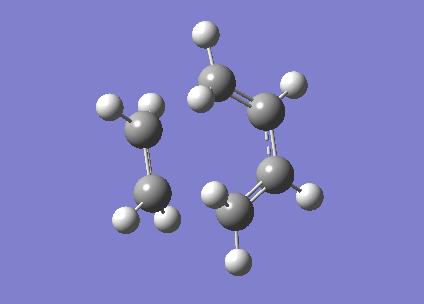Figure 30. Animated video of the the transition state.

The animated video of the vibrational modes confirms that the structure is the correct form of the cycloaddition transition state. By observing the HOMO and LUMO of the transition, it is found that both the orbitals are symmetrical. Two symmetric wavefunctions can mix to form a symmetric wavefunction and two anti-symmetric wavefunctions combine to also produce a symmetric wavefunction. The MO diagram obtained confirms that the transition state is formed from overlap of HOMO of cis-butadiene and LUMO of ethylene and vice versa.

Figure 31. A MO diagram of symmetric LUMO(left) and HOMO(right) of the reoptimized transition state.

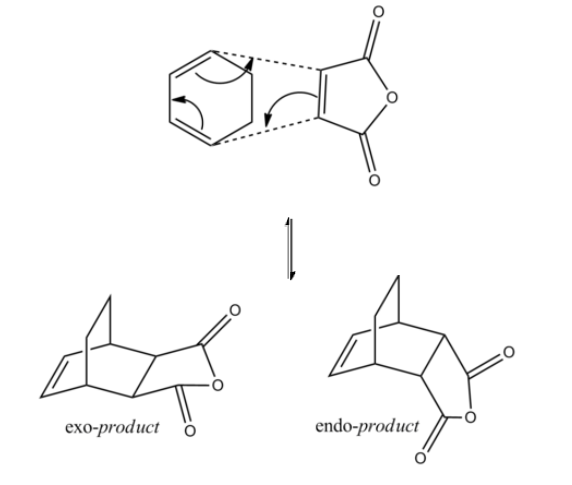
Reaction between maleic anhydride and cyclohexa-1,3-diene

The products formed from reaction between maleic anhydride and cyclohexa-1,3-diene show regio-selectivity. So there are two transition states formed which is given in the mechanism below in Figure 32.

Figure 32. A diagram showing the mechanism of the reaction between maleic anhydride and cyclohexa-1,3-diene

	Endo TS	Exo TS
Energy	-0.057	-0.049
Bond distance from terminal carbons	2.08	2.11
Structure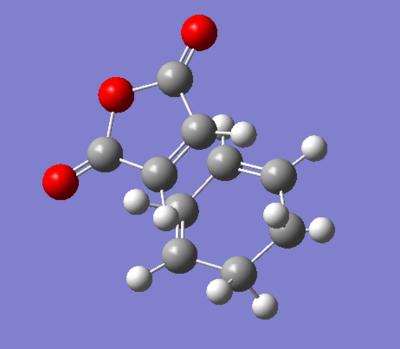

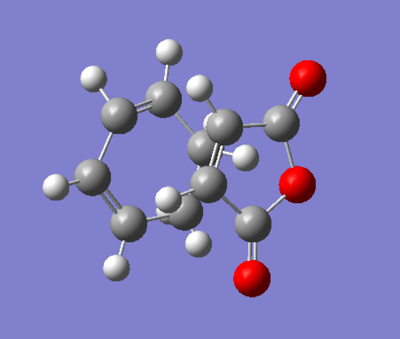
Figure 33. A table showing the structure of exo- and endo- transition state with its energies and bond distances.

By comparing the values of energy of the two transition states, it seems that the endo transition state is slightly lower in energy and therefore more stable than the exo transition state. This could be explained in terms of steric effects of exo, where there is an increased strain between the -(C=O)-O-(C=O)- part of maleic anhydride and the -CH2-CH2- of cyclohexa-1,3-diene moelcule.

The bond distance of the hydrogen atoms are approximately 2.83 Å from the central oxygen atom which is another indicator of torsional strain for the exo structure.For the endo- structure, the bond distance from H to central oxygen is higher by approximately 1.3 Å. The longer bond distance of endo significantly reduces the steric clash hence the lower energy of the molecule.

Conclusion

The computational modelling of the transition states using Gaussian was shown to be successful. It was possible to view the success of transitions state model by looking at its geometry and overall energy. Also, the modelling of the molecular orbitals and their overlap were studied to explain the overall stabilization of the molecules.

Improvements can be made with optimization at a higher level of theory. During the experiment, the minimum reaction path for both reactions could not be found due to failure of the application of the Intrinsic Reaction Coordinate. If given more time on the project, further investigation could have been done to see why the IRC method had failed.

---