User:Htw14
Computational Lab Year 3: Transition States and Reactivity
Introduction
The exercise sets out to understand transition states of reactions, an aspect often difficult to study by experimental means. Through obtaining minimas and transition structures(TS) from energy-optimising computations, as well as further elucidating reaction pathways and trajectory approaches, the study ultimately aims to determine reactivity using energy profiles generated from computed data of studied molecules.
The topic of interest in this wiki concerns the Diels-Alder reaction, a reaction highly powerful in the construction of cyclic compounds within organic synthesis. It is important to understand beforehand that the reactions offers high levels of predictability through stereoselectivity, which would be beneficial in predicting transition structures prior to any computational studies.
Originated from the strict rules of orbital symmetry conservation, such reactions are performed in concerted fashion, meaning that configurations of both reactants will be fully retained in the product, and thus are stererospecific. (For example, a cis alkene will always yield a syn product).
The two terms that would be referred to frequently in this wiki are 'Exo' and 'Endo'. These refer to yet another type of stereoselectivty in Diels-Alder reactions, which governs the position adopted by dienophile substituents relative to the diene system. Such selectivity is attributed to secondary orbital interactions, which will be discussed further in below sections.
Through combining mechanistic and stereoelectronic knowledge of the reaction with computation techniques (such as energy determination and MO visualisations), we would be able to correctly determine the specific diastereomers from reactions.This grants us the ability of disastreoselection control of mutiple stereogenic centered products, which is a powerful skill in organic synthesis.
In the following exercises, three different instances of the reaction are studied.
Nice intro but you should have defined a TS here.
Exercise 1: Butadiene with Ethene
Molecular Orbitals
MO Diagram
As shown below, the diagram illustrates what a standard MO diagram for a general Diels Alder reaction would have. Though butadiene and ethene are used to provide frontier orbitals as reactants here, according to substituents of different reactants, the relative energies of reactants and product orbitals in specific reactions may differ.
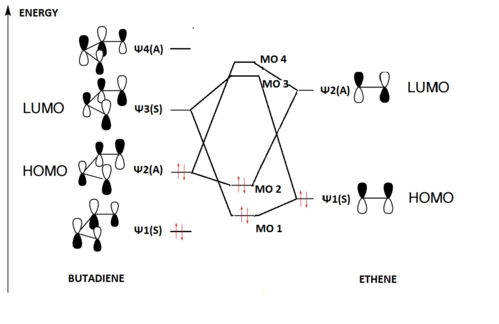
Symmetry requirement
For a successful reaction, symmetries of the HOMO and the LUMO must match, while violations to this will lead a forbidden reaction. These orbitals generated from wavefunctions can be either symmetric or anti-symmetric. As shown in the MO diagram, as frontier orbitals Ψ2 of butadiene and Ψ2 of ethene are both symmetric,a MO-forming interaction is allowed. An interaction of Ψ3 instead of Ψ2 however, would be forbidden as only A-to-A and S-to-S interactions are allowed. The expression of the overlapping intergral shown below illustrates this concept mathematically:
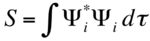
When S=0, this implies a zero overlap, which is typical when anti-symmetric and symmetric orbitals attmept to interact. On the other hand, any allowed overlap would have an S value in between close to 1, and these will be found in SS and AA overlaps.
Quantitative MO Visualisations
All MOs shown below correlates to the above MO diagram. It can be seen that the varying degree of delocalisation and shapes of the HOMOs and LUMOs correspond well with the phases of orbitals shown in the MO diagram.
|
|
|
| ||||||||||||
|
|
|
|
Reaction Analysis
Bond Formation and Lengths
As shown in the diagram below, relationships between atoms can be divided into three categories, two of which being covalent interactions (sp3 and sp2) whilst the other a non-bonding interaction. These distances can be defined as the covalent and Van der Waal radius respectively. Typically, the distances (in Angstroms Å) between two carbon atoms of these relationships are as follows: Van de Waal (VdW): 1.680 Å[1]; Covalent sp3: 1.537 Å[1]; Covalent sp2 : 1.347 Å[1]
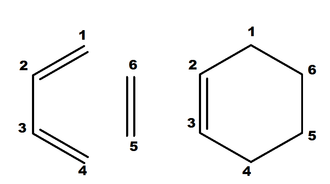
| Bonds | Reactant | Type | TS | Process | Product | Type |
|---|---|---|---|---|---|---|
| 1,2 | 1.33539 | sp2 | 1.37978 | Lengthen | 1.50090 | sp3 |
| 2,3 | 1.46834 | sp3 | 1.41107 | Shorten | 1.33784 | sp2 |
| 3,4 | 1.33539 | sp2 | 1.37978 | Lengthen | 1.50090 | sp3 |
| 4,5 | 3.41334 | 2VdW | 2.11461 | Shorten | 1.54040 | sp3 |
| 5,6 | 1.32736 | sp2 | 1.38177 | Lengthen | 1.54091 | sp3 |
| 6,1 | 3.41425 | 2VdW | 2.11469 | Shorten | 1.54041 | sp3 |
Firstly, it should be noted that the sum two Van de Waal radius of neigbouring atoms measures the internuclear distance of two non-interacting atoms prior to bond formation, hence it should be longer than those of bonding (i.e. sp2 and sp3). From the table, we can see that a smooth transition from non-bonding to sp3(shortening), sp3 to sp2 (shortening) and sp2 to sp3 (lengthening), thus turning the butadiene and alkene in to a cyclohexene in the process. As the alternating lengthening and shortening process of the bonds is yet another feature of the concerted process in the Diels Alder, the computated transiton state structure supports mechanism.
Vibrational Modes
|
|
The vibrational mode corresponding to the transition state agrees with the concerted nature of the Diels-Alder reaction, during which two sp3 bonds are formed synchronously. The resultant single imgainary frequency proves that a maximum has been reached in only one dimension on the potential energy surface, which verifies the existence of a transition structure. Next to it shows the lowest positive frequency mode,where the two reactants rotates in opposite directions of a 2D plane. In comparison, the illustration on the right is non-reactive and minute in energy, which matches well with a typical rotational mode.
Nf710 (talk) 18:26, 20 January 2017 (UTC) Nicely written section, however you havent shown an understanding of inverse/normal DA reactions
Exercise 2: Benzoquinone with Cyclopentadiene
Molecular Orbitals
The orbitals below illustrates the four key resultant molecular orbitals (MO1-MO4) from the MO diagram shown in Exercise 1, where in this case are derived from the four frontier orbitals of cyclopentadiene (the diene equivalent) and the two from Benzoquinone (the alkene equivalent). Both the Exo and Endo reactions computated in this exercise are cases of normal electron demand, the most common electronic interaction in Diels-Alder reactions, where the dienophile is electron poor while the diene being electron rich. On the other hand, inverse demand suggests the opposite, thus allowing that the alkene HOMO to be at a close energy level to interact strongly the the diene LUMO. If this is the case MO1 (referring to the MO Diagram above) will be the HOMO of the transition state as opposed to MO2. By examining phases from both HOMOs of the Exo and Endo approaches, this is evident that the reaction is not a case inverse demand, as both corresponded to the phase pattern that a MO2 equivalent would possess. We can therefore conclude that the reaction is in normal electron demand.
(Yes, this is true. How might the MO diagram in exercise 1 be adjusted to reflect this? Paying attention to the symmetry, you can see some of the MOs are swapped as a result of the MO energies changing in the reactants Tam10 (talk) 14:34, 4 January 2017 (UTC))
Exo Approach Key MOs
|
|
|
|
Endo Approach Key MOs
|
|
|
|
Reaction Analysis
Energetics and Pathway
Through analysing resultant thermodynamic data extracted from optimised structures of the reactants, products and transition states, a highly useful comparison could be made between the two reactant approaches. This will ultimately allow us to predict the reaction outcome expected in reality, thus showing the importance of computational techniques in chemistry. Such data is shown below:
| Energy(kJ/mol) | Exo | Endo |
|---|---|---|
| Reactant | -1510772.498 | -1510762.046 |
| Product | -1510782.951 | -1510783.751 |
| TS | -1510663.669 | -1510670.285 |
| Ea | 108.8296005 | 91.761225 |
| ΔE | -10.4521155 | -21.7050085 |
While the activation energy (Ea) gives information about the minimum energy input required to drive the reaction forwards, the total energy difference (ΔE) allows the judgement of the energy of stabilisation achievable for each reaction. From the table we see that less Ea is required initially, as well as a larger extent of stabilisation if the reaction were in the endo approach (reasons for this discussed in the below section). Therefore, we can conclude that the Endo adduct is both the Kinetic and Thermodynamic product.

Orbital Stereoelectronics
The endo reaction undergoes with dienophile benzoquinone sitting on top of the cyclopentadiene (Cp), which grants an additional opportunity for a favourable orbital interaction. As seen on the right, the p orbitals at the 2,3 position of Cp is within proximate distance to interact with the rear C=C π* orbitals of the dienophile, alongside the bond-forming front C=C π* orbitals. From the white arrows indicated, the Cp HOMO is also in correct phase to overlap with the second double bond of the Benzoquinone. This is known as a secondary orbital interaction, a stabilising interaction which does not involve bond formation.
Therefore, by having a second double bond within the same molecule in the dienephile, as opposed to a simpler alkene (eg. ethene), the additional interaction available plays the role in attracting the diene to adapt the Endo position while approaching. This lowers the activation energy of the Endo pathway, therefore transition structures are more favoured to be endo despite the associated sterics hinderance thermodynamically. This shows diels-alder reactions are often kinetically driven.
Nf710 (talk) 18:40, 20 January 2017 (UTC) Your energies are spot on, good understanding of the electron demand. The only thing that would have made this script better is if you had shown some understanding of the methods.
Exercise 3: Xylylene with Sulphur Dioxide
Reactant Approach via IRC
| Diels Alder Endo | Diels Alder Exo | Cheletropic |
|---|---|---|
|
|
|
Reaction Analysis
Energetics and Profile
The reaction of concern in the exercise introduces a possibility of a third reaction alongside the two approaches from the Hetero Diels Alder, known as the Cheletropic reaction. Again, computationally-calculated data of Gibbs free energy will be useful here to judge and compare the different reaction paths available, the reaction profile below should also provide a much clearer representation of how the three reactions compare:
| Energy(kJ/mol) | Exo | Endo | Cheletropic |
|---|---|---|---|
| Reactant | 177.69384 | 178.3790955 | 186.3606155 |
| Product | 56.3301025 | 56.983852 | -0.005251 |
| TS | 241.745538 | 237.7626545 | 260.08203 |
| Ea | 64.051698 | 59.383559 | 73.7214145 |
| ΔE | -121.3637375 | -121.3952435 | -186.3658665 |
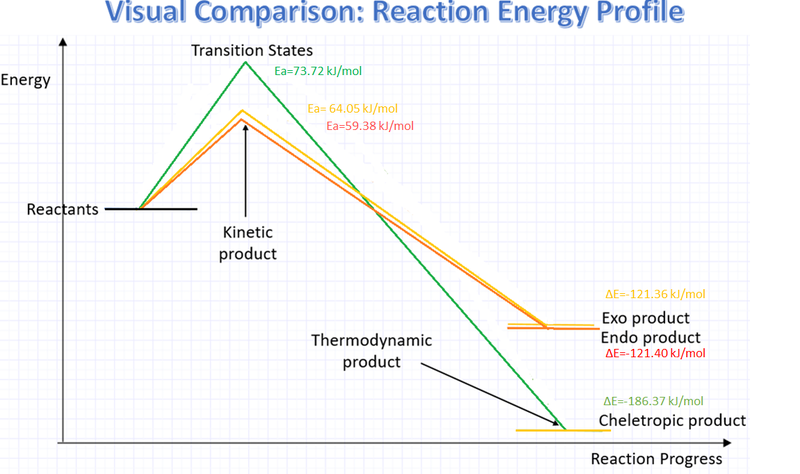
With the lowest energy activation energy amongst all, the Endo pathway can be concluded to be the Kinetic product. In terms of the overall energy change, although very similar, endo also appears as the more thermodynamically favourable between the two Diels-Alder reactions. Though given the small margin of difference, such a statement should be treated with discretion. It is however very clear that the Cheletropic pathway is the Thermodynamic product overall over Endo and Exo. This margin of difference that Cheletropic reactions show owes to the relatively stable five-membered adduct, as opposed to a six-membered one.
Having identified the KE and TD products, reactions conditions as well as solvents can be altered in order to obtain a desired product specifically.
Reactant Transformation
Through studying the reaction visualisations from above, we can see that as the reactive butadiene fragment in xylene cyclizes, a conjugated system can been seen to establish at the rear ring. As the major driving force for all three reactions,which are all 2π electrons away from satisfying the Huckel rule of 4n+2 delocalised electrons, the aromatisation of xylyene provides sufficient aromatic stabilisation energy to the reactants to interact.
(Be careful: "butadiene fragment in xylene cyclizes". This suggests the formation of a 4-membered ring Tam10 (talk) 14:34, 4 January 2017 (UTC))
Pathway Alternative
A second Diels-Alder reaction possibility comes at the rear diene, as part of the 1,3 cyclohexadiene system. Compared to the Exo and Endo diels-alder reaction computed above, the clear inability to aromatise in this alternative pathway, where a bridged ring system will give rise to a sizable thermodynamic penalty for both orientation approaches.Though the bridged system does not incur significant additional thermodynamic instability (because bonds formed and broken are identical to its aromatisable alternative, and that both S=O bonds in the products are pointing towards empty space), it does suffer from the following kinetic implication: The o-xylylene group, being originally a fully planar structure with a coplanar eight π-orbital system, is forced to distort from its conformation, as carbons at the 1,4 positions are essentially 'pushed' upwards, in order to accommodate the approaching sulpur dioxide. As this effect is present for both Exo and Endo approaches, Kinetic unavailability will also be realized across this alternative position for cyclisation. In conclusion, the thermodynamic stability for a reaction at the this diene would be high thermodynamically and kinetically disfavored over the the acyclic diene (whose reaction is illustrated and discussed in the above sections). Thus, the latter will be the the overwhelming major product.
(A good hypothesis. . It's not too difficult to try running the calculations however, and would give evidence supporting your hypothesis Tam10 (talk) 14:34, 4 January 2017 (UTC))
Conclusion
Throughout the exercises, recognising relationships of different calculations with the potential energy surface has been important in understanding what each step had meant. By grasping specific PES positions through calculations, useful information can be extracted for the different structures of concern (such as reactants,products and transition states). This has allowed energetic comparisons, molecular orbital interactions and reaction visualisation to be obtained and understood.
The most common calculation used was the minimisation, which is often used to obtain the lowest energy conformation of a molecule. From the PES surface, this is the global minimum as opposed to other local minimums, therefore approximating calculations were often ran beforehand to ensure the reliability of the obtained minimum values. Therefore, a standard protocol would be to perform a semi-empirical calculation (the rough approximation), before moving on to the B3LYP (the accurate calculation, a basis set based method involving both HF and DFT functions).
As transition states would also have zero gradients, second derivatives are required to differentiate between the two. Frequency calculations act as the key method of such verification, where a single imaginative force constant (the second derivative) would prove the achievement of a TS. This point should have all but one dimension amongst the 3N-6 dimensions minimised, leaving a maximum just a single dimension.
Given all the computation methods utilized throughout the task, it can be argued that the DFT-based B3LYP method is the most attractive: As although the quantum mechanical method DFT are able to produce relatively reliable approximations, this is in expense of poor results in terms of exchange correlations.The ab intito HF on the other hand, is highly effective in analytically solving exchange correlations, but as the method ruses electron positions, this requires higher degrees of freedom in the process of solving and thus suffers from longer computation times. Thus, putting both factors of accuracy and time penalty into perspective, as B3LYP which is able to solve exchange correlations accurately by using the same analytical approach as the HF , benefits from strengths of both methods mentioned above. Moreover, its accuracy is considered to have made up for its expensiveness in terms of time.
All in all, the applications used for this exercise has demonstrated just a small part of the capabilities in computation chemistry. Higher levels of accuracies (via basis sets) and calculations method (other Ab Initito implementations) has yet to be explored. Complex biological molecules modelling, reaction dynamics, excited electronic states just some other key examples where computations are of high utility to chemists.
References
- ↑ 1.0 1.1 1.2 Pauling, Linus and L. O. Brockway. "Carbon—Carbon Bond Distances. The Electron Diffraction Investigation Of Ethane, Propane, Isobutane, Neopentane, Cyclopropane, Cyclopentane, Cyclohexane, Allene, Ethylene, Isobutene, Tetramethylethylene, Mesitylene, And Hexamethylbenzene. Revised Values Of Covalent Radii". Journal of the American Chemical Society 59.7 (1937): 1223-1236. Web.
