User:Hs5017
Introduction to Molecular Modelling 2
Optimising a NH3 molecule
Summary Information of NH3
| Molecule Summary Information | ||||
|---|---|---|---|---|
| Calculation method | Geometry optimization DFT: B3LYP
Basis set: 6-31G(d,p) | |||
| Final energy | -56.55776873 au | |||
| RMS gradient | 0.00000485 | |||
| Point Group | C3V | |||
| N-H Bond Length | 1.01798 Å | |||
| H-N-H Bond Angle | 105.741° | |||
| Link to log file | File:HS5017 NH3 OPT.LOG | |||
Explanation of terminology
Final Energy: Energy calculated from the differentiation of the potential energy curve of the molecule to find its stationary point.
Basis Set: Identifies the 'resolution' of the optimization calculation
RMS gradient: Gradient close to the value of zero indicates that the energy value given above is at its stationary point.
However Gaussian can sometimes have errors in their optimization program so checking whether the optimization has run correctly by directly checking values has converged is necessary. We can find this from the log file of our molecule.
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000070 0.001800 YES RMS Displacement 0.000033 0.001200 YES
The crucial point here is to see that the maximum force is close to zero. Here we have a value of 0.00004 which is reasonable to accept as our stationary point to give its minimum energy.
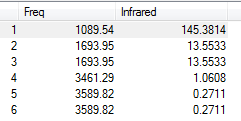
Vibrational Analysis of NH3
1. how many modes do you expect from the 3N-6 rule?
There are 4 molecules in NH3 so we expect 6 modes of vibration which we have.
2. which modes are degenerate (ie have the same energy)?
Modes 2 and 3, and 5 and 6 are degenerate as indicated by the same frequency value. This means that the same frequency is absorbed in altering the bond hence indicates that the modes are degenerate.
3. which modes are "bending" vibrations and which are "bond stretch" vibrations?
Modes 1 to 3 are bending and 4 to 6 are stretching. We can tell this because the frequencies absorbed for modes 4 to 6 are significantly larger. It takes more energy to stretch than bend abond.
4. which mode is highly symmetric?
Mode 2 and 4 as shown by the same changes of dipole moment for each mode.
5. one mode is known as the "umbrella" mode, which one is this?
Mode 1 mimics the motion of an umbrella.
6. how many bands would you expect to see in an experimental spectrum of gaseous ammonia?
4 bands as there are 4 different frequencies absorbed in creating 6 modes of vibration.
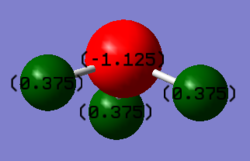
Charge distribution of a NH3 molecule
This is an expected result considering the difference in electronegativity of the two atoms. Comparing the electronegativity of the two atoms, N has a value of 3 and H has a value of 2.1. N is significantly more electronegative than H therefore drawing the electron density towards it hence has a negative charge, while H has a partial positive charge from the electron density drawn away. The overall charge of the atoms sum to 0 as the molecule is neutral.
Optimizing a H2 molecule
Summary Information of H2
| Molecule Summary Information | ||||
|---|---|---|---|---|
| Calculation method | Geometry optimization DFT: B3LYP
Basis set: 6-31G(d,p) | |||
| Final energy | -1.17853936 au | |||
| RMS gradient | 0.00000017 | |||
| Point Group | D*H | |||
| H-H Bond Length | 0.74279 Å | |||
| Link to log file | File:HS5017 H2 OPT.LOG | |||
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
Charge distribution of H2
A H2 atom has a charge distribution of 0 as it is a diatomic molecule that has no difference in electronegativity. Compare this to the vibrational frequencies of a NH3 molecule. H2 has a higher vibrational frequency because the N atom is much heavier than the H atom hence reducing inertia of the molecule.
Vibrational analysis of H2
a H2 molecule only has one mode of vibration which is a symmetric stretch. It has a high frequency of absorbtion because it has a small moment of inertia. The reduced mass is lower hence the atoms can vibrate at higher frequency. It has an infrared value of 0 because there is no dipole change as it is a diatomic molecule with the same electronegativity values.
Optimising a N2 molecule
Summary Information of N2
| Molecule Summary Information | ||||
|---|---|---|---|---|
| Calculation method | Geometry optimization DFT: B3LYP
Basis set: 6-31G(d,p) | |||
| Final energy | -109.52412867 au | |||
| RMS gradient | 0.00006156 | |||
| Point Group | D*H | |||
| N-N Bond Length | 1.10553 Å | |||
| Link to log file | File:HS5017 N2 OPT.LOG | |||
Item Value Threshold Converged? Maximum Force 0.000107 0.000450 YES RMS Force 0.000107 0.000300 YES Maximum Displacement 0.000033 0.001800 YES RMS Displacement 0.000047 0.001200 YES
Charge distribution of N2
Vibrational analysis of N2
Like the H2 molecule, the N2 molecule only has one mode of vibration as well which is a symmetric stretch. Compare this result to the vibrational frequency of a H2 molecule. It is significantly lower. This can be explained by the high moment of inertia of a N2 molecule experiences from its high atomic mass compared to that of H2 molecule therefore giving a lower vibrational frequency. Again, it has an infrared of 0 because there is no dipole moment.
Haber-Bosch reaction energy calculation
E(NH3)=-56.55776873 au 2*E(NH3)=-113.1155375 au E(N2)=-109.52412867 au E(H2)=-1.17853936 au 3*E(H2)=-3.53561808 au ΔE=2*E(NH3)-[E(N2)+3*E(H2)]=-0.05579071 au=-146.48 kJ/mol
Enthalpy is -146.48 kJ/mol indicating that the reaction is an exothermic reaction. The free energy of the reactants are higher than the products resulting in the negative free energy change and hence the stabalisation of reactants to the products. Hence we can conclude that gases are less stable in their diatomic states compared to NH3.
Optimising your own choice of molecule
Molecule Summary Information
| Molecule Summary Information | ||||
|---|---|---|---|---|
| Calculation method | Geometry optimization DFT: B3LYP
Basis set: 6-31G(d,p) | |||
| Final energy | -10529.67123680 au | |||
| RMS gradient | 0.00000246 au | |||
| Point Group | TD | |||
| Al-Br Bond Length | 2.32611 Å | |||
| Br-Al-Br Bond Angle | 109.471° | |||
Item Value Threshold Converged? Maximum Force 0.000005 0.000450 YES RMS Force 0.000003 0.000300 YES Maximum Displacement 0.000029 0.001800 YES RMS Displacement 0.000020 0.001200 YES
Vibrational Analysis of AlBr4-

As this is a non-linear molecule with a tetrahedral geometry, the number of modes of vibration is given by 3N-6 as well. We expect 3(5)-6=9 modes of vibration which we have.
Modes 1 and 2, 3 to 5 and 7 to 9 are degenerate. They indicate pairs or groups that have the same vibrational modes. Modes 1 to 5 are bending modes from the relatively low frequency of absorbance, and Modes 6 to 9 are stretching modes.
Modes 1 and 2 are scissoring motions of 2 pairs of the Br atoms where their planes of bending are perpendicular to each other. One pair can scissor in the xy plane (in the plane of the page) or the yz plane (out of the plane) which gives two mode of vibration each hence two degenerate modes.
Modes 3 to 5 are bending modes that scissor between 3 Br atoms and a single Al-Br bond unchanged such that it mimics an umbrella motion.
Mode 6 is a highly symmetric stretching mode. The Al atom is fixated and the 4 Br atoms stretch in the same direction as each other in phase.The frequency absorbed doubles from modes 4 to 6 from 102 Hz to 206 Hz indicating the significant increase in energy required to carry out this stretching motion.
Modes 7 to 9 are asymmetric stretching vibrations where the Br is fixed and the Al stretches significantly giving a high frequency of 408 Hz. This change in frequency from mode 6 can be explained from the motion of the Al atom rather than the Br atom. The frequency is inversely proportional to the moment of inertia where the heavier the atom, the lower the frequency absorbed. Therefore, with mode 7 to 9 the lighter Al atom moves while in mode 6 the heavier Br atom moves, hence giving a larger frequency for modes 7 to 9.
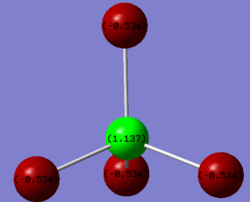
Charge distribution of AlBr4-
The Al atom bears a partial positive charge of 1.137 and the Br atoms bear a negative charge of -0.534 This is an expected result if we compare their electronegativity values where Al is 1.5 and Br is 2.8.
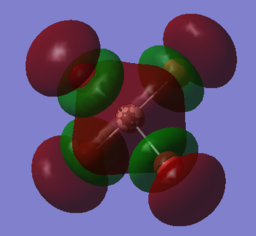
The energy of the orbitals are shown on the chk page when visualising the molecular orbitals. The MOs of interest were identified on the log files to find the contribution of each atomic orbital of each of the atoms as shown by the coefficients making up the MO. Only the coefficients and AO that significantly contribute to the MO are given in the table below. The higher the magnitude of the coefficient, the higher the contribution. The negative value indicates a destructive contribution of the AO on the MO.
| Molecular Orbital | Energy (eV) | Coefficients of contributing AOs from Al | Coefficients of contributing AOs from Br | Explanation |
|---|---|---|---|---|
| LUMO | 0.15202 |
4s: 0.93401 3s: 0.80932 |
2s: -0.24676 2pxyz:0.02097 3pxyz: -0.06493 4pxyz:0.11429 5pxyz:0.22850 |
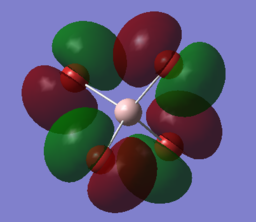
This is an anti-bonding orbital as shown by a nodal plane between the Al-Br bond. It has no electrons occupying it that allows it to accomodate electrons if a nucleophile were to attack. There is a significant contribution of AOs from the Al atom compared to the relatively diffuse contribution of the p orbitals from the Br atom. The pyrimidal MO shape on the Al atom supports the finding that the 6s is the most contributing from the aluminium atom as the the bromine p orbitals of all orientations x,y,z can overlap with the spherical s orbital. The coefficient of the s orbitals for the aluminium atom being close to 1 indicates that the s orbital contributes to the MO almost in its complete form. Contribution from the aluminium atom is significantly larger than the Bromine atom, hence yhis indicates that if a strong nucleophile were to attack the molecule, it would attack on to the Al atom where the LUMO predominantly resides at. |
| HOMO | -0.12453 | none |
1px:0.03929 1py:0 1pz:-0.03929 2px:-0.12103 2py:0 2pz:0.12103 3px:0.19683 3py:0 3pz:-0.19683 |
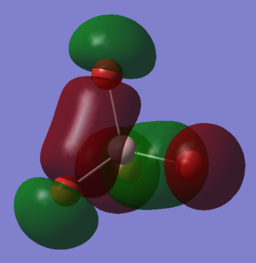
This is a non-bonding MO as indicated by the lack of electron density around the Al-Br bond. All of the AO from the aluminium atom has a coefficient of zero which indicates that there is zero contribution of the Al atom on the HOMO of the molecule. The electron density of this HOMO purely resides on the bromine atom. From the presence of two other degenerate MO indicates that the electrons are the lone pairs of the bromine atom in the valence 4p orbitals. However, this MO is also generated by the contribution of lower energy p orbitals of 2p, 3p, 4p and even some contribution of a higher 5p orbital. These p orbitals overlap to produce this diffuse HOMO which makes this such a good Lewis base. The HOMO is most close in energy to the non-bonding 4p orbitals. Therefore contribution to the HOMO from the other p orbitals decreases as you go lower in energy.
As mentioned earlier, there are three degenerate MOs but have different geometric contributions from the p orbitals. The MO is generated by the contribution of p orbitals in the same orientation, and none from the third orientation. Furthermore, the two contributing AOs have opposite signs on their coefficients showing that the MO is generated from the linear combination of two AOs out of phase with one another. The lack of contribution from the p orbital in the third orientation is because the AOs does not have the right geometry to overlap with one another. |
| 62nd MO | -0.60894 |
1s -0.01739 2s 0.08578 3s 0.15112 |
1s 0.02521 2s -0.16409 3s 0.19113 4s 0.33659 |
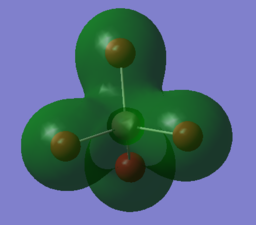
The MO is a bonding MO with no change of phases throughout the molecule. It is predominantly formed from the combination of s orbitals from both aluminium and bromine atom hence giving a spherical electron distribution on all of the atoms. The contributions of the s orbital on the bromine atom increases as the energy level increases for the better overlap with the 3s orbital of the aluminium. The lack of electron density near the aluminium atom, as seen by the empty spherical shape, can be accounted by the extremely low contribution from the 1s orbital from aluminium. Comparing the radial distribution of a 1s and 2s orbital, the 1s orbital much more compact than the 2s orbital. Therefore, the lack of contribution from the 1s of aluminium prevents the MO to spread its electron density in close proximity with the atom. |
| 69th MO | -0.19803 |
3px 0.27538 3py 0 3pz 0 |
3px -0.04377 3pyz -0.19007 4px -0.02336 4pyz -0.13942 |
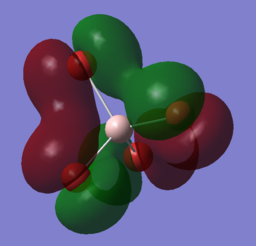
This is a bonding orbital where we finally see a contribution of the p orbitals from aluminum. The higher MO are all predominantly formed by the bromine's AO as the MOs are closer in energy to the orbitals of bromine which are higher in energy than aluminum. The fact that a p orbital from the aluminum atom contributes to the MO in a single orientation, it gives two 'barrel' structures of electron density above and below the atom. The fact that we have three degenerate MOs of this energy supports the fact that this MO exists in each of the x,y,z orientation, each time with only one orientation of the aluminum 3p orbital contributing to it. |
| 71st MO | -0.15118 |
3dxx -0.03479 3dyy 0.05952 3dzz -0.02472 |
3px -0.13529 3py 0.23142 3pz -0.09613 4px -0.12797 4py 0.21889 4pz -0.09093 |
The MO is a bonding MO with full electron occupancy. The MO is now so high in energy that there is contribution from the 3d orbitals from the aluminum atom. It is interesting to see that there is almost equal contributions of the 3p and 4p orbitals from bromine. This could be explained by the extremely diffuse shape of the 3d orbital of aluminum allowing overlap of p orbitals that are in separate principle quantum numbers. |