User:Ds2909mod3
The Cope rearrangement
Introduction
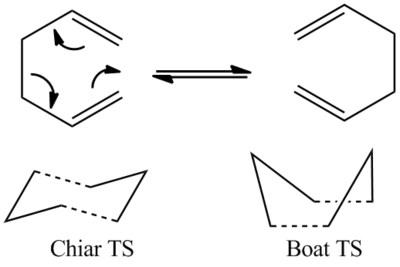
The Cope rearrangement is a landmark reaction in organic chemistry. Since its discovery in the 1940s [1] , its mechanism has sparked much interest leading to a multitude of experimental and computational studies in the past 50 years[2]. In the last two decades a consensus was reached that the reaction occurs in a concerted fashion via either a "chair" or a "boat" transition structure. The aim of the project is to locate the low-energy minima and transition structures on the C6H10 potential energy surface and to determine the preferred reaction mechanism.
Optimizing the Reactants and Products
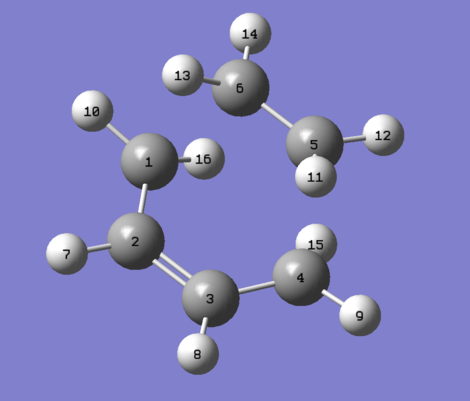
Using GaussView5, a molecule of 1,5-hexadiene was drawn. First the central 4 atoms were drawn with an sp3 configuration, putting them all in an anti-periplanar configuration (the dihedral angle was checked to be 180o), then the terminal atoms were set to sp2 configuration and finally the last two termini sp2 carbons were added. The structure was cleaned using the Clean function in Gaussview. The geometry was then optimised using the HF/3-21G level of theory. The summary of the calculation was examined and it the symmetry field was blank. The symmetrize function was used, and the symmetry was read from the Current point group field. The above were repeated with another molecule of 1,5-hexadiene this time with the 4 central carbon atoms set to a gauche linkage. The results are presented in Table 1 below
| Conformer | Anti2 (click for jmol) | Gauche4 (click for jmol) | |
|---|---|---|---|
| Point group | Ci | C1 | |
| Level of theory | HF/3-21G | HF/3-21G | |
| Total energy / a.u | -231.69254 | -231.69153 | |
| RMS gradient norm / a.u. | 0.00001891 | 0.00003354 | |
| Dipole moment / D | 0.01 | 0.13 | |
| Relative energy* / kcal/mol | 0.08 | 0.71 |
- Relative energy to most stable conformer
The Anti2 and Gauche4 conformations described in Appendix 1 of wiki lab script were obtained. The gauche conformer is higher in energy by about 0.63 kcal/mol, as expected from the secondary interactions that occur with the centre sp3 carbons. In the the anti conformer, there are two σC-H/σ*C-H and one σC-C/σ*C-C stabilizing interactions occur due to the anti-periplanar arrangement. In the gauche conformer, only one σC-H/σ*C-H interaction exists, and instead there is one σC-H/σ*C-C, and one σC-C/σ*C-H, both of which are less stabilizing. The gauche conformer gains some stabilisation due to the favorable 2.5A H-H close contacts of the olephinic hydrogens but this is not enough to overturn the electronic destabilisation. By modyfing the orientation of the double bonds, a few other stable 'anti' and 'gauche' conformations can be drawn. These were also optimised using the method above. The conformer with the minimum energy was taken as reference, and the relative energy of the other isomers was calculated.
| Conformer | Anti1 (click for jmol) | Anti3 (click for jmol) | Anti4 (click for jmol) | Gauche1 (click for jmol) | Gauche2 (click for jmol) | Gauche3 (click for jmol) | Gauche5 (click for jmol) | Gauche6 (click for jmol) |
|---|---|---|---|---|---|---|---|---|
| Point group | C2 | C2h | C1 | C2 | C2 | C1 | C1 | C1 |
| Level of theory | HF/3-21G | HF/3-21G | HF/3-21G | HF/3-21G | HF/3-21G | HF/3-21G | HF/3-21G | HF/3-21G |
| Total energy / a.u | -231.69260 | -231.68907 | -231.69097 | -231.68772 | -231.69167 | -231.69266 | -231.68962 | -231.68916 |
| RMS gradient norm / a.u. | 0.00002330 | 0.00001095 | 0.00000890 | 0.00001160 | 0.00000995 | 0.00000761 | 0.00002085 | 0.000001630 |
| Dipole moment / D | 0.01 | 0.00 | 0.30 | 0.32 | 0.38 | 0.34 | 0.38 | 0.32 |
| Relative energy / kcal/mol | 0.04 | 2.25 | 1.06 | 3.10 | 0.62 | 0.00 | 1.91 | 2.20 |
UPLOAD THE ACTUAL FILES AS PROOF
The results of the optimisations are in good agreement with the data in Appendix 1, with energies and point groups matching. Based on the same analysis as in the case of Anti2 and Gauche4, it would be expected that 'anti' conformers are lower in energy than 'gauche' conformers mainly due to the more stabilizing hyperconjugation experienced by the former. By looking at the relative energies, it can be seen that this is indeed the case: the average relative energy for the 6 gauche conformers is 1.42 kcal/mol whereas the one for the 4 anti isomers is 0.86 kcal/mol. It is surprising to see however, that the reference (i.e. the lowest energy conformer) is the gauche3 conformer. By looking at its structure it can be seen that the from all the other structures it has the most 'chair' like structure with the two double bonds in close proximity to each other. Computing the MOs of the molecule reveals the reason why this conformer is so favored: a secondary orbital interaction between the pi clouds of the two alkenes, lowering the energy of the HOMO. As can be seen from the computed HOMO of the molecule there is considerable overlap in an antarafacial fashion between the pi clouds of the two double bonds.
The Anti2 HF/3-21G structure was re-optimised at the DFT-B3LYP/6-31G(d) level, and below comparison is made with the results obtained using HF.
| Parameter | HF/3-21G | DFT-B3LYP/6-31G(d) | Literature value[3] |
|---|---|---|---|
| Energy / a.u | -231.69254 | -234.61170 | N/A |
| C=C bond/ A | 1.32 | 1.33 | 1.34 |
| =C-C bond /A | 1.51 | 1.50 | 1.50 |
| C-C bond / A | 1.55 | 1.55 | 1.54 |
| Central dihedral angle / o | 180 | 180 | 180 |
A direct comparison of the energy between the HF/3-21G and the DFT-B3LYP/6-31G(d) is not possible because they are complete different methods which use different approximations. The DFT-B3LYP/6-31G(d) method is more complex and should be more 'accurate'; the energy is expected to be more negative as the method uses more Slater Functions to model the system but the geometry suffers little changes.
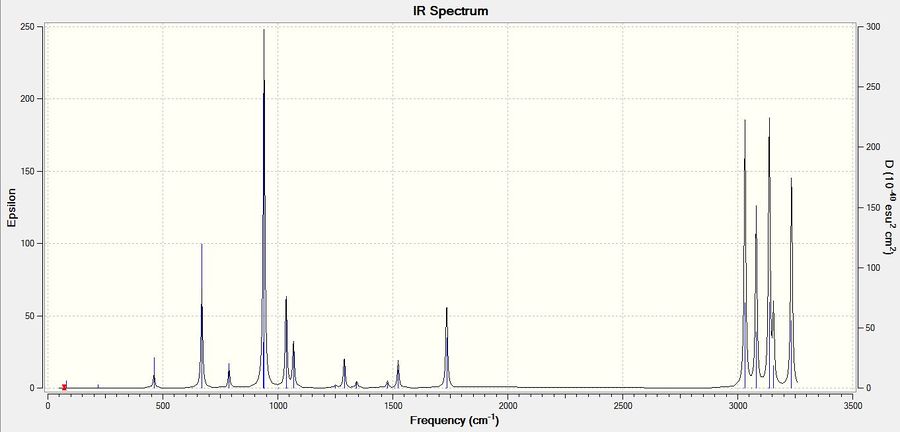
An frequency calculation is needed to ensure that the obtained structure is an actual energy minima. The frequency analysis is effectively the second derivative of the Potential energy curve, hence if all the frequencies are positive, the PE curve is 'convex up' (i.e. an energy minima), if one negative frequencies appears it means we have a transition state and if more than one negative frequencies appear it means that the structure was not optimised successfully. Starting from the DFT-B3LYP/6-31G(d) optimised structure a frequency calculation was performed at the same level of theory.
The log file of the calculation can be found here. All the frequencies were positive, confirming that the obtained minima is genuine. The simulated IR spectra can be found below.
More information can be found by exploring the log file:
Sum of electronic and zero-point Energies= -234.469212 Sum of electronic and thermal Energies= -234.461856 Sum of electronic and thermal Enthalpies= -234.460912 Sum of electronic and thermal Free Energies= -234.500821
Optimising the Chair and Boat Transition Structures
The transition state of the Cope rearrangement can have two possible conformations: a C2h chair conformation or a C2v boat conformation. In this section both of these conformations will be studied using different computational methods in order to determine the most likely transition state structure.
Chair optimisation
An allyl fragment (CH2CHCH2) was drawn and optimised at the HF/3-21G level of theory. Using two optimised allyl fragments a 'chiar' like transition state was built with the distance between the two allyl fragments set to 2.2 Å. Transition state optimisations are more difficult than minimisations because the calculation needs to know where the negative direction of the curvature is (i.e. where the actual transition state lies on the reaction coordinate). This requires manual optimisation of the transition state, and in the following section the chiar like transition state will be optimised using two different methods: the TS (Berny) Method and the Freeze Coordinate Method.
The Transition State (Berny) method
Starting from a reasonable guess of the transition state geometry, the force constant matrix (also known as the Hessian) is computed in the first step which will then be updated as the optimisation proceeds. However this may not work if the guess structure for the transition state is far from the actual structure, where curvature on the Potential Energy Surface may be quite different. This is done by selecting Opt+Freq in the Job type in the calculation setup together with choosing the Optimisation to a TS(Berny). The force constant were calculated only Once and 'Opt=NoEigen' keyword was added to stop the calculation from crashing if more than one negative frequencies were detected which is quite a likely scenario if the guess for the transition state structure is not good enough. The results are presented in Table 4:
| Optimised structure | Imaginary frequency animation |
|---|---|
 |
 |
| Energy / a.u. | -231.619322 |
| ΔE* / kcal/mol | 46.0 |
| Imaginary frequency / cm-1 | 818 |
| Point group | C2h |
| C-C bond lenght / Å | 1.39 |
| Allyl fragments separation / Å | 2.02 |
| C-C-C angle/ o | 120 |
- Difference in energy relative to the lowest energy conformer gauche3.
As can be seen from the results in Table 4, the imaginary frequency is at 818 cm-1, the animation shows the concerted process of bond forming and bond breaking in good agreement with the concerted mechanism of the reaction. Evidence that support the homo-aromatic transition state present in peryclic reactions are present: sp2hybridisation of all carbons, delocalised structure with C-C bonds all the same lenght, 1.39 A, intermediate between single C-C bonds (1.47 A) and double bonds 1.40 A. A transition state barrier (or Activation Energy) can also be calculated by comparing the energy obtained here to the one of the lowest energy structure at the HF/3-21G level obtained in the previous section: 46.0 kcal/mol.
The Freeze Coordinate Method
To overcome the difficulty of both optimising the transition state and following the reaction coordinate which can lead to false results if the geometry guess is not good enough, the two are separated into individual tasks. Thus the first step is to freeze the reaction coordinate and minmising the rest of the molecule. This is done in the Redundant Coordinate Editor by using Freeze Coordinate and Specify Value to 2.2A option on the two terminal carbons from the ally fragments which form/break a bond during the rearrangement. The structure is the minimised using the same HF/3-21G method. Using the minimised structure, the previous frozen bonds were optimised by changing Freeze Coordinate to Derivative and doing a minimisation this time.
| Optimised structure | Imaginary frequency animation |
|---|---|
 |
|
| Energy / a.u. | -231.619322 |
| ΔE / kcal/mol | 46.0 |
| Imaginary frequency / cm-1 | 818 |
| Point group | C2h |
| C-C bond lenght / Å | 1.39 |
| Allyl fragments separation / Å | 2.02 |
| C-C-C angle/ o | 120 |
It can be seen that the result is identical to the one of previous method, with the same geometry and 818 cm-1 imaginary frequency obtained. This confirms that the transition state geometry guess in the TS(Berny) method was good enough. For larger systems this approach would be preferable as it harder to make a good guess of the transition state structure.
Boat optimisation
The QST2 method will be used to obtain the geometry of the boat transition state. In this method, reactants and products can be specified and the calculation will interpolate between the two to try and find the transition state. Firstly, because the reactant and product are both 1,5-haxadiene, the product molecule was manually edited so that it corresponded to the numbering obtained if the reactant had rearranged.
In the Gaussian Calculation Setup the Job type was set to Opt+Freq, optimising to a Transition State with the TS(QST2); the level of theory was HF/3-21G. The job failed to converge; upon examining the chk file, the structure looked like the chair transition, but more dissociated. This was due to the fact that the starting guessed transition state structure is very far from the sought boat structure and the programme only translated the top allyl fragment without even consider the possibility of a rotation around the central bonds.
The initial gjf file was reloaded and manually modified so that the two molecules are closer to the boat transition structure.
The QST2 calculation was re-run and this time it converged.
| Optimised structure | Imaginary frequency animation |
|---|---|
 |
 |
| Energy / a.u. | -231.602802 |
| Imaginary frequency / cm-1 | 840 |
| ΔE / kcal/mol | 56.4 |
| Point group | C2v |
| C-C bond lenght / Å | 1.38 |
| Allyl fragments separation / Å | 2.14 |
| C-C-C angle/ o | 121.6 |
The presence of a single negative frequency at 840 cm-1 confirms that the obtained structure is the boat transition state. As with the chiar transtion state, the bond breaking/bond forming process occurs in a concerted manner. The HF/3-21G level of theory puts the boat transition state structure 10.0 kcal/mol highier than the chair. The fragments are also farther apart by 0.1 Å, in good agreement with the higher energy of the boat transition state
Intrinsic Reaction Coordinate (IRC) Method
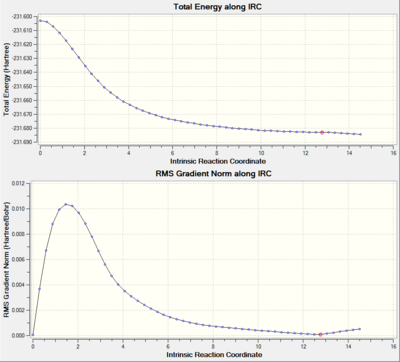
Looking at the transition state structures, there is no way to tell which of the 10 conformers correspond to the starting material leading to the transition state. Here the Intrinsic Coordinate Method will be used to follow a minimm energy path from the transition state structure down to its local minimum on a potential energy surface. This is done by creating a series of points and taking small geometry steps in the direction where the slope of the energy surface is steepest. Because the reaction coordinate is symmetrical in this example, only the forward direction will be computed with the number maximum number of steps set to 50 at first.
Intrinsic Reaction Coordinate of the Chair Transition state structure
| IRC last structure | Intrinsic reaction coordinate animation |
|---|---|
 |
 |
| Energy / a.u. | -231.68907 |
| ΔE / kcal/mol | to calc |
| Point group | C2 |
| C1-C6 bond lenght / Å | 1.56 |
| C1-C2 bond lenght / Å | 1.52 |
| C2-C3 bond lenght / Å | 1.32 |
| central C-C-C-C dihedral/ o | 68.9 |
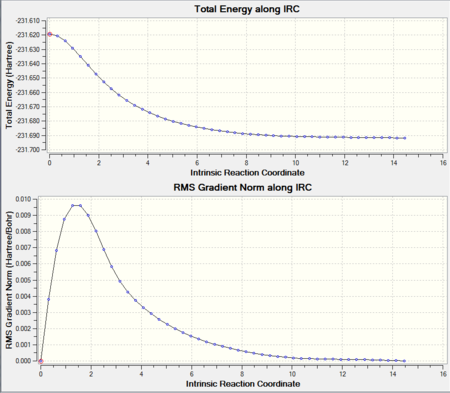
It can be seen that the energy minima has not yet been reached. There are 3 options to complete the calculation: a) run a normal minimisation on the last point (i.e. the closest point to the eneergy minima structure). This would be the fastest method but has the downfall that if started too far away from the local minima it may not reach it and return possibly another local minima en-route to the south local minima. b) redo the IRC and specify a larger number of points until it reaches a minimum. This approach is more reliable than a) but has the same pitfall that if too far away from the minima it may also end up with a wrong minimum. c) redo the IRC the option to compute the force constants at every step (i.e. until no more negative frequencies are present.This is the most reliable approach but also the most expensive in term of computational cost and time, and it may become unfeasable for larger systems.
Since our system is small, it is withing computational reach of option c).
| IRC last structure | Intrinsic reaction coordinate animation | |
|---|---|---|
 |
 | |
| Energy / a.u. | -231.69165 | |
| ΔE / kcal/mol | 0 | |
| Point group | C2 | |
| C1-C6 bond lenght / Å | 1.55 | |
| C1-C2 bond lenght / Å | 1.51 | |
| C2-C3 bond lenght / Å | 1.32 | |
| central C-C-C-C dihedral/ o | 65.4 |
It can now be seen that the calculation did converge and the structure of the gauche4 isomer has been obtained.
Intrinsic Reaction Coordinate of the Boat Transition state structure
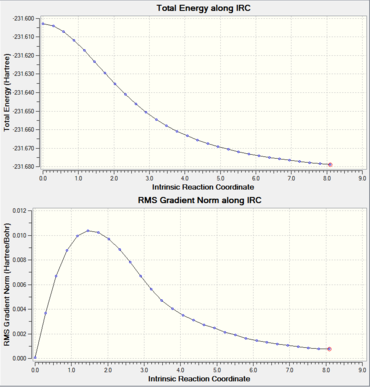
| IRC last structure | Intrinsic reaction coordinate animation |
|---|---|
 |
 |
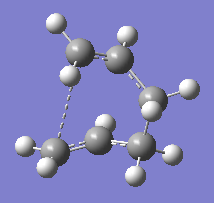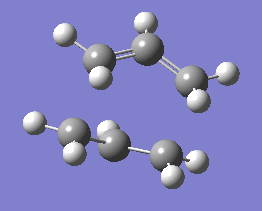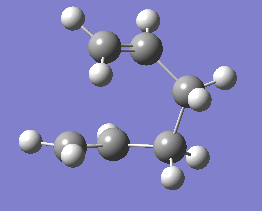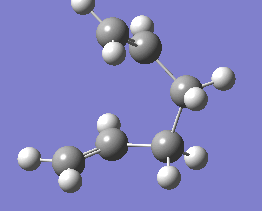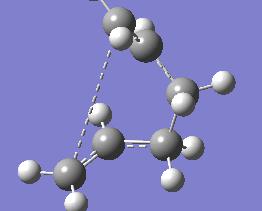| Energy / a.u. | -231.67891 |
| ΔE / kcal/mol | to calc |
| Point group | C1 |
As with the chiar IRC, the calculation did not reach the energy minimum. The IRC was redone specifying to compute the force constants at every step and the step number was increased to 100.
| IRC last structure | Intrinsic reaction coordinate animation |
|---|---|
 |
|
| Energy / a.u. | -231.68566 |
| ΔE / kcal/mol | to calc |
| Point group | C2 |
In the 50 steps of the IRC it seems that it reached a local minimum corresponding to the gauche 1 conformer, then it went on further to try on find the global minimum. The energy reported above corresponds to the local minimum energy.
Calculating the activation energies
The chiar and boat HF/3-21G optimised structures were re-optimised and their force constants calculated with the B3LYP/6-31G* level of theory.
| Chiar TS | Boat TS | |
|---|---|---|
| HF/3-21G energy/ a.u. | -231.6193 | -231.6028 |
| Activation energy HF/3-21G (0K) / kcal/mol | 45.2 | 56.4 |
| HF/3-21G imaginary frequency/ cm-1 | 818 | 840 |
| B3LYP/6-31G* energy / a.u. | -234.5570 | -234.5413 |
| Activation energy B3LYP/6-31G* (0K) / kcal/mol | 36.2 | 42.7 |
| B3LYP/6-31G* imaginary frequency / cm-1 | 566 | 530 |
The experimental activation energies are 33.5 ± 0.5 kcal/mol via the chair transition structure and 44.7 ± 2.0 kcal/mol via the boat transition structure at 0 K. It can be seen that the values computed with the B3LYP/6-31G* are in good agreement with literature values.
The Diels Alder Cycloaddition
The Diels Alder reaction of butadiene with ethene is a type of peryclic reaction in which the π orbitals of the dieneophile are used to form new σ bonds with the π orbitals of the diene. This is a concerted process and the conservation of orbital symmetry dictates if the reactions are allowed or forbidden. Here we will look at the transition state structure of and .... at the symmetry of orbitals to help predict if a reaction is allowed or not;
Optimising the reactants
Budadiene and ethene were sketched and optimised using the AM1 semi-empirical molecular orbital method. The HOMO and LUMO of the two molecules was then visualized and the orbitals were assigned their symmetry with respect to the plane of the molecule.
| Butadiene HOMO | Butadiene LUMO | Ethylene HOMO | Ethylene LUMO |
|---|---|---|---|
 |
 |
ethene HOMO !! Ethene LUMO | |
| Anty-Symmetric | Symmetric | Symmetric | Anti-Symmetric |
It can be seen that the butadiene LUMO - ethylene HOMO and butadiene HOMO - ethylene LUMO pairs are of the same symmetry and can interact.
Computating of the Transition State geometry
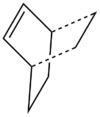
Knowing that the transition state of the reaction has an envelope geometry, the starting point was the bicyclo system on the right. The first step was sketching a cyclohexane in the chiar conformation, adding the -CH2-CH2- bridge, using the Clean function to tidy up the structure and and optimising it at the AM1 level. The optimised structure was modified to look like the transition state: one of the -CH2-CH2- fragments was deleted, the bonds were deleted to the remaining -CH2-CH2- fragment and the distance between the two was increased to 2.2 A. The structure was then optimised as the transition state TS (Berny) using the AM1 semi-empirical molecular orbital method.
| Optimised structure | Imaginary frequency animation |
|---|---|
 |
 |
| Energy / a.u. | 0.11165468 |
| ΔE / kcal/mol | 46.0 |
| Imaginary frequency / cm-1 | 956 |
| fragments separation (C1-C6 and C4-C5 bond lenghts) / Å | 2.12 |
| C3-C4 bond length / Å | 1.38 |
| C2-C3 bond length / Å | 1.40 |
| C5-C6 bond length / Å | 1.38 |
| H(9)-C(4)-H(15) angle / o | 114.8 |
| H(11)-C(5)-H(12) angle / o | 115.3 |
As can be seen there is only one imaginary frequency at 956 cm-1 corresponding to forming two bonds between the two fragments in a concerted manner, confirming that the structure at hand is the transition state. All the bond lenghts are very close and intermediate between a C-C single bond, 1.54 Å, and a C=C double bond, 1.34 Å. The 1.38 Å - 1.40 Å bonds look more like benzene 1.40 Å, in good agreement with the homo-aromatic delocalised transition state of peryciclic reactions. As the van der Waals radius of the C atom is 1.70 Å, two carbon atoms at less that their combined van der Waals radius (3.4 Å) should be able to exchange electron density. The butadiene-ethylene separation is 2.12 Å, which is larger than a C-C single bond but smaller than the van der Waals radius of two carbons, hence there is a bond forming process in place. This is better illustrated in Table 7, where significant overlap can be seen between the pi clouds of the two alkenes. The butadiene C1 and C4 and the ethylene carbons are begining to rehybridise to from sp2 to sp3 as can be seen from the angles which have departed from the 120o ideal sp2 angle towards the 109.5 ideal sp3 angle.
The imaginary frequency corresponds to a synchronous bond forming process between the butadiene and ethylene in good agrrement with the concerted nature of peryciclic reactions. The lowest positive frequency is at 147 cm-1 and corresponds to asynchronous twisting of the two fragments. This is expected to be the lowest frequency since the butadiene-ethylene bonds are weaker. Nevertheless, the fact that it involves both fragments implies significant electronic overlap between the two.
| HOMO | LUMO |
|---|---|
 |
 |
| Anti-symmetric | Symmetric |
In can be seen that the HOMO of the transition state is Anti-symmetric, since it is formed butadiene HOMO and ethylene LUMO both of which are anti-symmetric. The opposite is true for the LUMO: it is formed from butadiene LUMO and ehylene HOMO, both of which are symmetric, hence the transition state LUMO is symmetric. Since all of the components of the reaction are suprafacial, i.e. the HOMO-LUMO interactions ca take place, the [4πs + 2πs] thermal reaction is allowed.
Studying the regioselectivity of the Diels Alder Reaction
Cyclohexa-1,3-diene 1 undergoes a facile [4πs + 2πs] cyclo-addition with maleic anhydride 2 to give primarily the endo adduct. This is known as the Endo rule and is a consequence of the reaction being kinetically controlled, with the endo transition state being lower in energy. Here we will look at the two transition states to try and rationalise this behaviour.
Locating the transition state structures
As the systems are larger than the dealt with so far, The Freeze Coordinate method was used for both the endo and the exo. The low level AM1 semi empirical molecular orbital method was used first. After the transition state structure was obtained it was re-optimised using the DFT-B3LYP/6-31G* for better accuracy in order to compare energies.
| Exo TS | Endo TS | |
|---|---|---|
| Optimised structure |  |
 |
| Imaginary frequency animation |  |
 |
| Total Energy / a.u. | -612.6793 | -612.6834 |
| Imaginary frequency / cm-1 | 448 | 447 |
| Fragments separation (C3-C8 , C6-C7 bond lenghts)/ A | 2.29 | 2.27 |
| C2-C3 bond length / A | 1.39 | 1.39 |
| C2-C3 bond length / A | 1.40 | 1.40 |
| C7-C8 bond length / A | 1.40 | 1.39 |
| C9-C4, C11-C13 distance / A | 3.02 | 2.99 |
| C9-H17, C11-H16 distance / A | 2.53 | N/A |
| Exo TS MOs | Endo TS MOs | |
|---|---|---|
| HOMO |  |
 |
| HOMO-1 |  |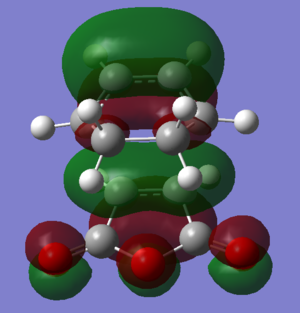
 |
| HOMO-2 |  |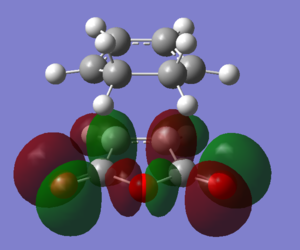
 |
The DFT-B3YP/6-31G* calculation places the Exo transition state 0.0041 Eh or 2.6 kcal/mol higier in energy than the endo transition state, in good agreement with the endo structure being a kinetic product. The difference in enegy can be rationalised based on a combination of steric and electronic factors. By looking at the structure of the optimsed exo transition state, it can be seen that the -(C=O)-O-(C=O)- has a steric clash with the -CH2-CH2- fragment. The C9-C4, C11-C13 distance is 3.02 A, less than the combined van der waals radius of two carbon atoms, 3.4A. Similarly the C9-H17, C11-H16 distance is 2.53 A, whereas the combined van der Waals radius of the two is 2.89 A. In contrast, in the endo transition state, the steric clashed are much diminished since the opposing -CH=CH- fragment is flat and occupies much less space. There is also a favorable secondary orbital overlap interaction between the -(C=O)-O-(C=O)- and the -CH=CH- fragment (see below).
From an electronic point of view, the endo transition state is stabilised by secondary orbital interactions between the -(C=O)-O-(C=O)- group and the newly forming double bond. In the HOMO-1 of the endo transition state, in phase overlap between the π cloud of the C=O bonds and the π* orbital of the newly forming bond can be seen; in the HOMO-2, in phase overlap is seen between the π orbital of the newly forming double bond and one of the oxygen lone pairs. It should also be noted that these interactions occur in the HOMO-1 and HOMO-2 and not in the HOMO because the C=O and O based Fragment Orbitals are lower in energy due to the presence of the electronegative oxygen whereas the HOMO is only based on less electronegative carbon.
Conclusion
Computational methods have been successfully used to obtain the boat and chair transition states of the Cope rearangement of 1,5-hexadiene and rationalise that the reaction proceeds via concerted fashion via chair transition state starting from the gauche2 conformer.
In the Diels Alder Cycloaddition the stereselectivity was rationalised using secondary orbital interactions in the transition state.
References
- ↑ Cope, A. C.; Hardy, E. M. J. Am. Chem. SOC. 1940,62,441
- ↑ Graulich, N. (2011), ChemInform Abstract: The Cope Rearrangement — The First Born of a Great Family. ChemInform, 42: no. doi: 10.1002/chin.201148231
- ↑ Yates T., J Am Chem, 1972 , vol. 94, p. 3074,3075 DOI:10.1021/ja00764a031