User:Ds2909mod2
Introduction
In this module, ab initio-DFT calculations are used to predict and rationalise the properties of small molecules. Ab initio refers to the fact that the calculations are 'from scratch', by directly solving the Schrodinger Equation (with the appropriate approximations), with no inclusion of experimental data. DFT refers to solving for the total energy in terms electron density rather than the wavefunction. The basis set refers to how the atomic orbitals function are expanded to create molecular orbitals. It is important to notice that different calculations using different methods and basis sets are not comparable, because they all use different approximations. In this project the DFT-B3LYP/LANL2MB and DFT-B3LYP/LANL2DZ methods were used the most and only calculations using the same method were compared.
Optimising BH3
A BH3 molecule was sketched in GausView05 and the B-H bond length was set to 1.5A. An optimization using the DF3-B3LYP method and the 3-21G basis set was performed.
The molecule was then inspected and the B-H bond lenght was found to be 1.193A and the H-B-H angles 120o in good agreement with literature[1] values of 1.19 A and 120o. It is interesting to note that at room temperature BH3 exists as the dimer B2H6, a molecule which has D2h symmetry and 3c-2e bonding and has puzzled chemists with an unusual up until the 1940s when its correct structure was proposed by H. Christopher Longuet-Higgins, which was still an undergraduate at that time. In order to obtain and study BH3, the authors of the paper had to use high temperature gas IR spectroscopy in which BH3 was generated by breaking down B2H6using electrical discharges. Thus, even using a very simple method and basis set, properties were predicted with surprisingly good accuracy.
A summary of the calculations and result is presented below; the actual optimization file can be found here
BH3 optimisation File Name = BH3_OPT_OUTPUT File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = 3-21G Charge = 0 Spin = Singlet E(RB3LYP) = -26.462 a.u. RMS Gradient Norm = 0.00020672 a.u. Imaginary Freq = Dipole Moment = 0.000 Debye Point Group = D3H Job cpu time: 7.0 seconds.
The .log file was checked to see if the calculation had converged. As can be seen from below the calculations did converge and a stationary point was found.
Item Value Threshold Converged?
Maximum Force 0.000413 0.000450 YES
RMS Force 0.000271 0.000300 YES
Maximum Displacement 0.001610 0.001800 YES
RMS Displacement 0.001054 0.001200 YES
Predicted change in Energy=-1.071764D-06
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1935 -DE/DX = 0.0004 !
! R2 R(1,3) 1.1935 -DE/DX = 0.0004 !
! R3 R(1,4) 1.1935 -DE/DX = 0.0004 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
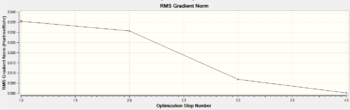
In order to find the optimised geometry, Gaussian starts from the initial imputed geometry, assumes the nuclear position is fixed (i.e. it makes use of the Born-Oppenheimer approximation) and calculates Schrodinger's Equation for the electrons. Thus in the first step, Gaussian calculates an energy E(R1) and a densisty rho(R1) for the nuclei in positions represented by R1. Then Gaussian solves for the position of the nuclei: the nuclei are moved and the first step above is repeated for each geometry. If a geometry with a lower energy is found, E(R2) < E(R1), then the whole cycle restarts from R2 and it keeps going until the lowest energy geometry is found. The gradient is calculated at each geometry, to be at the bottom of the Potential Energy Surface means having a gradient of 0, or very close to 0. Below is the graphical representation of the cycle described above; it can be seen that the job converged in 4 steps, and that the Root Mean Square of the gradient of the energy is <0.001.
| Total Energy | RMS gradient | Animation |
|---|---|---|
 |
 |
 |
IR frequency analysis
A frequency analysis was performed in order to determine if the obtained structure is in fact a minima (and not a Transition State/false global minima).The frequency analysis is effectively the second derivative of the Potential energy curve, hence if all the frequencies are positive, the PE curve is 'convex up' (i.e. an energy minima), if one negative frequencies appears it means we have a transition state and if more than one negative frequencies appear it means that the structure was not optimised succesfully.
IR Calculation.log file
| No | Form of virbration | Frequency | Intensity | Symmetry |
|---|---|---|---|---|
| 1 |  |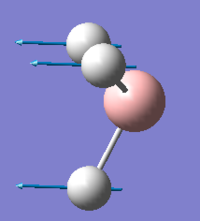
1144, lit.[2]1141 | 92.87 | A2`` |
| 2 |  |
1204 lit2. 1204 | 12.31 | E` |
| 3 |  |
1204 lit2 1204 | 12.31 | E` |
| 4 |  |
2598 lit N/A | 0.00 | A1` |
| 5 |  |
2737 lit* [3] 2592 | 103.74 | E` |
| 6 |  |
2737 lit3* 2592 | 103.74 | E` |
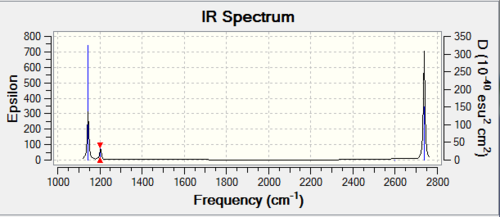
The predicted IR spectra include 6 vibrations (3N-6). However the actual computed spectra only has 3 peaks. This is due to the fact that 2 vibrations are degenerate ( (in plane rocking-in place scissoring; the two asymmetric stretches) and the A1` vibration is not IR active.
Molecular orbitals of BH3
Molecular orbitals have been computed using the DF3-B3LYP method and the 3-21G basis set DOI: http://hdl.handle.net/10042/to-9854. The resulting MOs are compared with the 'ones made by hand' using the LCAO method.
| Orbital | Energy /eV |
| 1a1' | -183.02 |
| 2a'1 | -14.14 |
| 1e' | -9.74 |
| 1a2' | -2.01 |
| 2e' | 5.22 |
| 3a'1 | 5.41 |
As can be seen from the figure on right, the computed MOs resemble the ones derived by hand, and the relative ordering of the orbitals is well predicted* which aids in rationalizing the Lewis acidity of BH3 by having a LUMO low-lying p-orbital in which it can accept electron density. However, it only provides us with a qualitative picture, and computational calculations provide a much accurate (quantitative) picture. *It is difficult to assign the order of the 2e` and 3a` orbitals and a reasonable assignment can be made on the basis that s-s anti-bonding interaction in 3a` being larger than the s-p antibonding interaction in the 2e`. This is confirmed by the calculations: the 3a` is slightly higher in energy by 0.19eV than the 2e`. Another useful number is the energy of the empty p-orbital, -2.01 eV which is clearly negative (i.e. it is favorable to accept electrons) and it also gives insight into what makes a good donor, for example NH3, in which the HOMO lone pair has a 2.26 eV energy[4] (i.e. almost perfect for HOMO-LUMO interaction and donation).
NBO analysis
NBO analysis takes a delocalised MO picture and computes an 'organic chemist' 2 electron-2 centre picture of bonding; i.e. where the electron density from the bond lies.
| Charge separation in terms of colour | Quantitative NBO charges |
|---|---|
 |
 |
As can be seen from the picture above, boron is bright green, which indicates indicates highly positive charge, as expected because the boron atom which is Lewis deficient is highly positively charged. Bright red indicates highly negative charege, thus the hydrogen atoms tend to have hydride character.
The graphical interface of GaussView5 only provides a limited set of information. Much more useful information can be found by examining the .LOG file. Thus the Summary of Natural Population Analysis:, which is the information displayed graphically in the pictures above can be found:
Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
B 1 0.33161 1.99903 2.66936 0.00000 4.66839
H 2 -0.11054 0.00000 1.11021 0.00032 1.11054
H 3 -0.11054 0.00000 1.11021 0.00032 1.11054
H 4 -0.11054 0.00000 1.11021 0.00032 1.11054
The ''Bond orbital/ Coefficients/ Hybrids'' section can provide insight into the bonding of the molecule in terms of contribution from each atom, and moreover contribution from each orbital.
1. (1.99853) BD ( 1) B 1 - H 2
( 44.48%) 0.6669* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.0000 0.0000
0.8165 0.0000 0.0000 0.0000
( 55.52%) 0.7451* H 2 s(100.00%)
1.0000 0.0000
2. (1.99853) BD ( 1) B 1 - H 3
( 44.48%) 0.6669* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 55.52%) 0.7451* H 3 s(100.00%)
1.0000 0.0000
3. (1.99853) BD ( 1) B 1 - H 4
( 44.48%) 0.6669* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 -0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 55.52%) 0.7451* H 4 s(100.00%)
1.0000 0.0000
4. (1.99903) CR ( 1) B 1 s(100.00%)
1.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000
5. (0.00000) LP*( 1) B 1 s( 0.00%)p 1.00(100.00%)
Thus the first three occupancies are bonding orbitals (BD); the three B-H bonds; 44.49% of each bond is contributed from the B orbitals which have a hybridisation of 33%s+66%p (i.e. normal sp2), while 55.51% of the bond comes from the H orbital which is 100%s. The 4th occupancy is the B 1s core electrons, which do not participate in bonding; the last occupancy is the B empty p orbital which is 100% p. Another useful section is the Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis which outlines the various interactions between various MOs, like mixing and secondary interactions. In this case this section is not populated, as there are no significant interactions. If however, the molecule at hand would be BCl3 one would expect to see interactions between the Cls lone pairs and the empty p-orbital.
Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis
Threshold for printing: 0.50 kcal/mol
E(2) E(j)-E(i) F(i,j)
Donor NBO (i) Acceptor NBO (j) kcal/mol a.u. a.u.
The last section provides a summary of the NBO analysis; including a negative energy on the B lone pair (i.e. empty p orbital).
Natural Bond Orbitals (Summary):
Principal Delocalizations
NBO Occupancy Energy (geminal,vicinal,remote)
====================================================================================
Molecular unit 1 (H3B)
1. BD ( 1) B 1 - H 2 1.99853 -0.43712
2. BD ( 1) B 1 - H 3 1.99853 -0.43712
3. BD ( 1) B 1 - H 4 1.99853 -0.43712
4. CR ( 1) B 1 1.99903 -6.64476 10(v),11(v),12(v)
5. LP*( 1) B 1 0.00000 0.67666
6. RY*( 1) B 1 0.00000 0.37177
7. RY*( 2) B 1 0.00000 0.37177
8. RY*( 3) B 1 0.00000 -0.04532
9. RY*( 4) B 1 0.00000 0.43446
10. RY*( 1) H 2 0.00032 0.90016
11. RY*( 1) H 3 0.00032 0.90016
12. RY*( 1) H 4 0.00032 0.90016
13. BD*( 1) B 1 - H 2 0.00147 0.41201
14. BD*( 1) B 1 - H 3 0.00147 0.41201
15. BD*( 1) B 1 - H 4 0.00147 0.41201
-------------------------------
Total Lewis 7.99463 ( 99.9329%)
Valence non-Lewis 0.00441 ( 0.0551%)
Rydberg non-Lewis 0.00097 ( 0.0121%)
-------------------------------
Total unit 1 8.00000 (100.0000%)
Charge unit 1 0.00000
TlBr3 analysis
TlBr3 was drawn in Gaussview, its point group restricted to D3h and was optimised using the DFT-B3LYP method. The basis chosen was LanL2DZ because it uses pseudo-potentials to model core electrons for group 2 and below elements (which for a molecule with 181 electrons speeds up calculations considerably) and can take into account the relativistic effects which heavier elements experience and which the Schrodinger equation does not take into account.
The resulting Tl-Br bond lenght and Br-Tl-Br bond angles were 2.65 A and 120o. The values are in good agreeement with the ones found in literature[5] of 2.51A for the bond length and 120o for the angle. Note that TlBr3 is very unstable and the cited paper the measurement was made in water, where TlBr3 is tough to coordinate with 2 molecule of water to form a trigonal bypiramidal species. Nevertheless the bond lenght value is more than accurate given the simplicity of the technique.
TlBr3 geometry DFT-B3LYP/LANL2DZ optimization output
Frequency analysis
In order to determine that the obtained structure is in fact an energy minima and not a Transition state (or an un-optimised structure) a frequency analysis needs to be carried out (as discussed in the previous section). TlBr3_Frequency.LOG file
| Vibration | Frequency/ cm-1 | Intensity/ e | Symmetry label |
|---|---|---|---|
| Scissoring | 46 | 4 | E` |
| Rocking | 46 | 4 | E` |
| Wagging | 52 | 6 | A2`` |
| Symmetric Stretch | 165 | 0 | A1` |
| Asymmetric Stretch | 211 | 25 | E` |
| Asymmetric Stretch | 211 | 25 | E` |
The same vibration modes available to BH3 are available to TlBr3 as they both have the same D3h geometry. What differs is the the actual magnitude, the TlBr3 one are about an order or magnitude smaller, reflecting the weaker Tl-Br bonds. Given the fact that thermal energy is about 220 cm-1 all the above modes are expected to be populated; thus the molecule would be in its highest vibrational state, very close to dissociating. It is also interesting to note that the E` scissoring mode is now lower in energy that A2`` wagging mode, probably due to the sterics involved in bringhing closer 3 bulky Br atoms.
By looking inside the .log file a number of Low frequencies can be found.
Low frequencies --- -3.4213 -0.0026 -0.0004 0.0015 3.9367 3.9367 Low frequencies --- 46.4289 46.4292 52.1449
These correspond to translating the molecule and ideally they should be as close to 0 as possible. Here some vibrations are at 46 and 52 cm-1; with a more accurate method and basis set these would probably disappear.
What is a bond?
A bond between elements A and B happens when the two atoms are put close enough in distance so that their AO wavefunctions can overlap to produce MOs leading to an overall system stabilization. The optimum distance is considered to be the ground state of the molecule AB. In the early days of Chemistry, a bond was viewed as a exclusive 2c-2e interaction but as Chemistry evolved it was clear that more complex bonding, like the 3c-2e bonding found in B2H6 can exist. In the diagram on the left, two Hydrogen atoms are approaching each other from infinite distance. The stabilizing interaction starts to take place at more than 2 A (3 times the equilibrium bond length), thus a bond exists even if H is excited to a state where the bond length is 1.5A. The environment and rest of bonding in the system can play a big role in the equilibrium bond length, and what is a ground state length for a bond in a system may be correspondent to an excited state in another system. For example
What happened to the bonds in Gaussview?
Gaussian has a predefined value range for bonds which is derived from organic molecules. As is the case for the P-Cl bonds in the task below, Gaussian removed the bonds as they exceeded a predefined length. That does not mean that there are no bonds there, only that the equilibrium bonds distance for an inorganic complex is different from that of an organic purely covalent molecule.
Cis-trans isomerism
Introduction
The complex cis-Mo(CO)4(PPh3)2 isomerises when refluxed in toluene to the thermodinamically more stables trans isomer [6]. A quick method of determining is the trans isomer had formed is to do an IR analysis; the cis isomer has 4 IR C=O stretches whereas the trans has only one. The aim of this project is to rationalize this behavior using computational tools. Because the phenyl groups would be too computationally demanding, these are replaced with Cl groups, which should provide us with meaningfull data whilst minimizing computational cost.
Optimising the strucutures
The two complexes were drawn in Gaussview5; first the DFT-B3LYP method, using the low level basis set LANL2MB and loose convergence criteria, was used to get a rough geometry. The summary of the data is found below: cis optimisation log trans optimisation log
| Cis isomer | Trans isomer |
|---|---|
cisiso_opt File Name = cis_lanl2mb_output File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2MB Charge = 0 Spin = Singlet E(RB3LYP) = -617.52509161 a.u. RMS Gradient Norm = 0.00000306 a.u. Imaginary Freq = Dipole Moment = 8.6274 Debye Point Group = C1 Job cpu time: 39.2 seconds. |
od2_trans_iso_LANL2DZ_input File Name = trans_lanl2mb_output File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2MB Charge = 0 Spin = Singlet E(RB3LYP) = -617.52209141 a.u. RMS Gradient Norm = 0.00001167 a.u. Imaginary Freq = Dipole Moment = 0.2998 Debye Point Group = C1 Job cpu time: 16 minutes 28.6 seconds. |
Although the method can supply good bond lenght and angles, dihedral angles are often poorly optimised. Taking the B3LYP/LANL2MB structure, as instructed by the lab script, the dihedral angles of the formed by the PCl3 group were manually modified. For the cis conformer, one Cl was set to point up parallel to the axial bond, and that one Cl of the other group points down; for the trans isomer, the PCl3 groups were set in an eclipsed geometry with one Cl of each group parallel to one Mo-C bond. A new B3LYP optimisation was performed on the structures, this time using the more accurate LANL2DZ basis set and with int=ultrafine scf=conver=9 added to increase electronic convergence.The results are displayed below:
| Cis isomer | Trans isomer |
|---|---|
 File Name = cis lanl2dz File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2DZ Charge = 0 Spin = Singlet E(RB3LYP) = -623.57707194 a.u. RMS Gradient Norm = 0.00000767 a.u. Imaginary Freq = Dipole Moment = 1.3095 Debye Point Group = C1 Job cpu time: 1 hours 11 minutes 39.1 seconds. |
 File Name = trans_lanl2dz File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2DZ Charge = 0 Spin = Singlet E(RB3LYP) = -623.57603100 a.u. RMS Gradient Norm = 0.00003328 a.u. Imaginary Freq = Dipole Moment = 0.3051 Debye Point Group = C1 Job cpu time: 49 minutes 2.7 seconds. |
Cis LANL2DZ opt log Trans LANL2DZ opt log
However, the LANL2DZ pseudo-potential and basis set does not take into account the low-lying D orbitals of the P atom, which contribute to bonding and further stabilisation of the complex. In order to add these, manual editing of the a .gjf file derived from the last optimisation is needed. Thus, at the begining of each file the word extrabasis was added after the line begining with a # and at the end of the file the text which adds a D function to the P atoms with a decay rate of 0.55 0.100D+01:
(blank line) P 0 D 1 1.0 0.55 0.100D+01 **** (blank line)
The .gjf file was resubmitted for optimisation:
| Cis isomer | Trans isomer |
|---|---|
cis_LANL2DZ_withD File Name = cis_LANL2DZ_withD_output File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = Gen Charge = 0 Spin = Singlet E(RB3LYP) = -623.6929 a.u. RMS Gradient Norm = 0.00005559 a.u. Imaginary Freq = Dipole Moment = 0.0714 Debye Point Group = C1 Job cpu time: 38 minutes 17.5 seconds. |
trans_LANL2DZ_withD_input File Name = trans_LANL2DZ_withD_output File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = Gen Charge = 0 Spin = Singlet E(RB3LYP) = -623.6941 a.u. RMS Gradient Norm = 0.00000798 a.u. Imaginary Freq = Dipole Moment = 0.2293 Debye Point Group = C1 Job cpu time: 43 minutes 39.4 seconds. |
Cis including D functions Trans with D functions
Relative energy comparison
Looking at the last optimasaton, which takes into account the low-lying D orbitals of Phophorus, the trans isomer is more stable by 3.2 kJ/mol. Thus one would expect that the cis isomer, would isomerise at room temperature to the trans isomer. However, this is from the thermodynamic point of view. The isomerisation reaction proceeds via a Dissoaciative Mechanism, involving the breaking of one of the Mo-P bonds, thus the isomerisation is kinetically controlled. It has been shown however that there is an alternative isomerisation mechanism, which occurs if the phosphorus ligands have a cone angle of less than 132o. P(Ph)3 has a cone angle of 145 whereas PCl3 has a cone angle of 125o(thus it has a lower activation pathway). This is a shortfall of the compatational analysis made here; it cannot be said with certainty if the cis-Mo(CO)4(PCl3)2 will isomerise to the trans isomer at room temperature. Given the low predicted energy separation between the two isomers it will be a matter of weather sterics or electronics govern the stability. From a steric point of view, the cis isomer is disfavored as it has two bulky PCl3 groups adjacent to each. However the cis isomer is favored from an electronic point of view due to the trans effect, donation of electron density from the P lone pair to the trans C=O pi* low lying empty orbital. In our optimised cis structure the C=O bond is 0.02 A longer for the trans C=O. The opposite apply to the trans isomer, it is favored from a sterics point of view (as it puts the bulky phosphorus ligands 180o to each other) but it is disfavored from an electronic point of view (trans effect cannot occur). One way to overturn the thermodicamic stability of the cis isomer would be to introduce a favorable interactions between the PX3 ligands. One could envisage putting OH groups (making H bonding), replacing the PX3 ligand all together with something smaller like H2O (which can also H bond) or using med-chem methods such as sticking a CH2-CF3 group instead of the Cls.
Bond lengths and angles
| Mo-P bond lengths | Mo-P lit. value[7](A) | P-Mo-P angle(o) | P-Mo-P lit.value(o) | ||
|---|---|---|---|---|---|
| Cis | 2.48 | 2.58 | 94 | 94 | |
| Trans | 2.42 | 2.50 | 177 | 180 |
Given the fact that the PPh3 ligands have been replaced by PCl3, the obtained values are in very good agreement with literature; both shorter which can be rationalised in the terms of the smaller cone angles of the PCl3 group compared to the PPh3 group, allowing ligands to come closer and form a shorter bond. The trans effect can be seen on the Mo-P bonds: in the cis isomer, back donation occurs, strengthening (and thus shortening) the Mo-P bond by 0.08 A.
Frequency analysis
An IR frequency analysis is done to ensure the obtained geometry the actual minimum. There were no negative frequencies confirming that the obtained geometry is the actualy minima. There were however, a few very low frequencies: Cis frequency calculation .log Trans frequency calculation .log
| Isomer | Form of vibration | Frequency/cm-1 | Intensity | |
|---|---|---|---|---|
| Cis | Paralel rotation of the PCl3 ligands  |
12 | 0 | |
| cis | Antiparalel rotation of the PCl3 ligands  |
20 | 0 | |
| trans | Paralel rotation of the PCl3 ligands  |
4 | 0 | |
| trans | Antiparalel rotation of the PCl3 ligands  |
7 | 0 |
These correspond to free rotation of the PCl3, as the thermal energy at room temperature is about 220 cm-1 these as populated at room temperature. Note that this is in the gas phase or in solution, in the crystal structure, free rotation probably does not exist. This has important consequences when designing for example ligands for asymmetric synthesis, ideally one single rotamer should exits. One way of locking the conformation would be linking the two ligands together, for example with an alkyl group.
It is also interesting to note that the paralel rotation is lower in energy for both the cis and the trans; and that the rotation barrier is highier in the cis isomer (12 and 20 cm-1 in the cis vs. 4 and 7 in the trans) as expected due to the steric clash of rotating the PCl3 ligands past one another in the cis isomer.
C=O stretching frequencies
| Frequency / cm-1 | Frequency lit. value / cm-1 | Intensity | Symmetry label |
|---|---|---|---|
| 1938 | 1986 | 1604 | B2 |
| 1942 | 1994 | 813 | B1 |
| 1952 | 2004 | 588 | A1 |
| 2019 | 2072 | 545 | A1 |
| Frequency / cm-1 | Frequency lit. value / cm-1 | Intensity | Symmetry label |
|---|---|---|---|
| 1939 | 1896 | 1606 | Eu |
| 1940 | 1896 | 1606 | Eu |
| 1966 | N/A | 6 | B1g |
| 2025 | N/A | 6 | A1g |
For the cis isomer, which has C2v symmetry, the irreducible representation is 2A1+B1+B2, all of these lead to a change in dipole moment thus 4 C=O vibrations are expected. The trans effect is also visible here, the C=O pair which is not trans to a phosphorus ligand has the highest C=O vibration, 2019 cm-1.
For the trans isomer, which should have D4h symmetry, using the reduction formula we arrive at A1g+B1g+2Eu, thus 4 vibrations are predicted. However, only the degenerate Eu vibrations lead to a change in dipole moment and therefore only one IR peak is expected. The reason why the 2Eu are not degenerate (but off by 1 cm-1) and the appearance of the two very faint B1g and A1g absorbtions is the fact that the symmetry of the molecule was not restricted to D4h, but instead was calculated as C1.
Mini Project - Analysing and comparing the XeF4, XeF3Cl and XeF2Cl2 molecules
Introduction
Since the discovery of the first noble gas compound in 1962, XeFPtF6, a variety of noble gas compounds which break the 'octet rule' have been prepared. In particular Xe shows the widest spectrum of chemistry; in recent years even organo-xenon compounds with a Xe-C bond have been prepared[8]. This mini-project will look at the rare gas combinations XeF4, XeF3Cl, and cis and trans XeF2Cl2. While XeF4 is a known compound, the rest have not been reported and even though they are only theoretical, looking at their electronic structure and bonding should be very interesting.
First, the structure and geometry of the 4 molecules will be examined and compared, then a frequency analysis will take place, electronic structure, MOs and NBOs will be analyzed. All calculations were done using the same method and basis set: the DFT-B3LYP method and LANL2DZ basis set. The LANL2DZ basis set was chosen because it uses pseudopotentials to model core electrons of group 2 and below elements (thus shortening computational time and cost at minimal loss of accuracy) and can model the relativistic effects experienced by heavier elements which are not taken into account by the Schrodinger equation. First each molecule was drawn using GW5 and optimised. The first challange was actually to draw the square planar Xe, as there was only the option to draw Xe as an atom or with an octahedral geometry. Initially, the swaure planar XeF4 moelcule was made tetrahedral IF4 and then editing the .gjf. After doing the optimisation and frequency calculation, negative frequencies were discovered, indicating that the obtained minima was a false one. This happened with all the molecules, which were drawn starting from the IF4 molecule. An analysis of the .gjf file revealed the culprit: IF4 molecule is actually a doublet, i.e. 0 2. modifying the file to 0 1, fiexed the problem. In the end the method of starting from a octahedral Xe, deleting two axial atoms and adding the F and Cl atoms was chosen.
| XeF4 | XeF3Cl | cis-XeF2Cl2 | trans-XeF2Cl2 |
|---|---|---|---|
Title Card Required File Name = XeF4_geom_opt File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2DZ Charge = 0 Spin = Singlet E(RB3LYP) = -414.5246 a.u. RMS Gradient Norm = 0.00000183 a.u. Imaginary Freq = Dipole Moment = 0.0000 Debye Point Group = D4H Job cpu time: 14.0s |
XeF3Cl geom opt File Name = XEF3CL GEMOPT# File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2DZ Charge = 0 Spin = Singlet E(RB3LYP) = -329.6409 a.u. RMS Gradient Norm = 0.00000417 a.u. Imaginary Freq = Dipole Moment = 0.8110 Debye Point Group = C2V Job cpu time: 55.0s |
cis geom opt File Name = CIS_GEOM_OPT File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2DZ Charge = 0 Spin = Singlet E(RB3LYP) = -244.7590 a.u. RMS Gradient Norm = 0.00000083 a.u. Imaginary Freq = Dipole Moment = 1.2880 Debye Point Group = C2V Job cpu time: 46.0s |
Title Card Required File Name = TRANS_GEOM_OPT File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2DZ Charge = 0 Spin = Singlet E(RB3LYP) = -244.7671 a.u. RMS Gradient Norm = 0.00001167 a.u. Imaginary Freq = Dipole Moment = 0.0000 Debye Point Group = D2H Job cpu time: 21s |
As can be seen from the output summary, all optimasations have converged (the RMS << 0.001), the assigned point group and dipole moments are in good agreement with expectation. Thus the XeF4 molecule has D4H simmetry and o dipole moment, XeF3Cl is C2v and has a dipole of 0.81D, cisXeF2Cl2 is C2v and has a dipolo of 1.28, trans XeF2Cl2 is D2h and has no dipole moment.
From the optimised geometries bond lenght and angles can be gathered and comapred to literature.
| ' | XeF4 | XeF3Cl | Cis-XeF2Cl2 | transXeF2Cl2 |
| Xe-F bond length / A | 2.09 | 2.10 cis/ 2.14 trans F | 2.15 | 2.11 |
| Xe-Cl bond length / A | / | 2.66 | 2.69 | 2.75 |
| F-Xe-F angle | 90 | 89.6 | 85.2 | 180 |
| Cl-Xe-F angle | / | 90.4 | 90.9 | 90 |
| Cl-Xe-Cl angles | / | / | 92.9 | 180 |
The predicted bond length of 2.09A and D4h geometry for XeF4 is in good agreement with the literature value[9] of 1.98 A and D4h symmetry. Data for the other compounds is not available. It can be seen that replacing F atoms with more electropositive Cl atoms, has the effect of lengthening of the Xe-F bond. In XeF3Cl, there are two Xe-F bonds lenghts, and Cl seems to have a trans effect of lengthening the Xe-F trans. The same effect is present in cis-XeF2Cl2, the trans Xe-F bond lenght, 2.15 A is comparable to the one is XeF3Cl 2.14A. The same effect is seen in the trans XeF2Cl2, where Xe-Cl exibits its trans effect on another Xe-F. The Xe-Cl bond is lengthened by 0.06A compared to the cis isomer.
Frequency analysis
In order to determine weather the obtained conformational was actually a minima, a frequency analysis must be performed to check that there are no negative frequencies. As can be seen from the tables below, there are no negative frequencies, confirming that we are at a minima.
XeF4_freq.log XeF3Cl_freq.log cisXeF3Cl2_freq.log transXeF2Cl2_freq.log
| Vibration | Frequency / cm-1 | Intensity / ε | Symmetry (D4h p.g.) |
2 X In plane orthogonal degenerate bend  |
122 | 5.70 | Eu |
Out of plane scissoring  |
136 | 0 | A2g |
In plane scissoring  |
165 | 0 | B2g |
Wagging  |
231 | 62.85 | A2u |
Symmetric concerted stretching/compression of F-Xe-F trans bonds  |
428 | 0 | B1g |
Xe-F Symmetric stretch of all bonds  |
446 | 0 | A1g |
2 X degenerate trans F-Xe-F Assymetric stretch  |
524 | 111.49 | Eu |
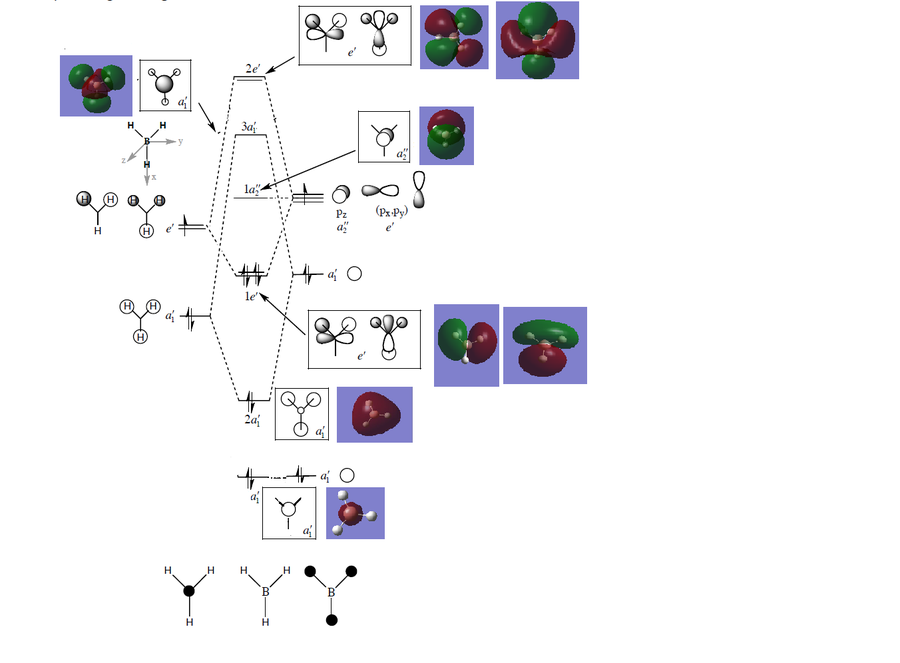
For XeF4 there are 9 frequencies present but only 3 absorption bands in the IR spectra. This is due to the fact that quite a few vibrations are not IR active because there is no change in dipole moment and some are degenerate. The out of plane and in plane scissoring vibrations, A2g and B2g lead to no change in dipole moment as they are both concerted and in an opposite direction thus they are not IR active. The same applies to the B1g mode, where the change in dipole accompanied by the stretching of two trans Xe-F bonds is compensated by the compression of the other Xe-F bonds; the A1g mode is totally symmetric and does not lead to a change in dipole moment. The two Eu bending modes are degenerate, while the assymetric Eu stretches are also degenerate. This leaves us with only 3 peaks corresponding to 5 vibrations, 2 degenerate Eu in plane bend modes, 2 degenerate asymmetric stretches and the A2u wagging mode. In terms of the magnitude of the actual bond stretching modes (which give an indication of the bond strength), these are in the region of 500 cm-1, much less than the C-F 1000 cm-1, but comparable to the transition metal M-X stretches.
| Vibration | Frequency / cm-1 | Intensity / ε | Symmetry (C2v p.g.) |
Cl-Xe-f in plane bend  |
84 | 3.40 | B2 |
Cl-Xe-F out of plane bend  |
108 | 1.29 | B1 |
F-Xe-F in plane bend  |
132 | 2.80 | A1 |
In plane scissoring (all bonds) |
138 | 0.25 | B2 |
F-Xe-F out of plane bend  |
200 | 43.47 | B1 |
Cl-Xe-F asymmetric stretch |
255 | 2.79 | A1 |
F-Xe-F symmetric stretch  |
427 | 0.01 | A1 |
Cl-Xe-F asymmetric stretch |
440 | 86.37 | A1 |
F-Xe-F asymmetric stretch  |
514 | 100.73 | B2 |
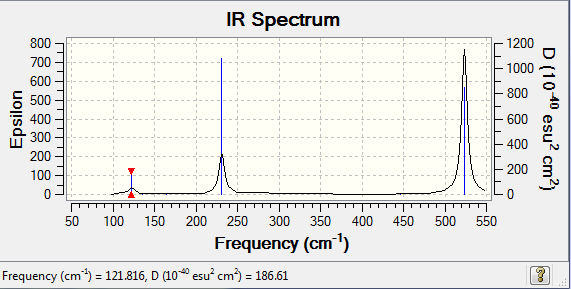
The XeF3Cl spectra has now much more peaks reflecting the lower symmetry of the molecule; with the presence of the Cl atoms now most of the frequencies lead to a change in dipole moment and thus are IR active. Replacing a F atoms with a Cl has a significant effect on the frequencies. The lowest energy modes now correspond to vibrations involving the Cl atom, with the Cl-Xe-F in plane bend at only 84 cm-1, while the lowest bond stretch is now at only 255 cm-1 compared to 428 cm-1 in XeF4, reflecting the weaker bond made with the Cl atom. Interestingly the F-Xe-F in plane bend in XeF3Cl is highier in energy than then corresponding one in XeF4: 132 vs. 122 cm-1. This can be explained in terms of sterics, more energy is needed to put the F atoms next to the bulkier Cl. The F-Xe-F symmetric and asymmetric stretches have now decreased in XeF3Cl (446 vs.427 for the symmetric stretch and 514 vs 524 for the asymmetric stretch) reflecting the effect of introducing the highier energy AOs of Cl to forms slightly higher in energy delocalised MOs (and thus weaker bonds and vibrations).
| Vibration | Frequency / cm-1 | Intensity / ε | Symmetry (C2v p.g.) |
Clorine atoms in plane bend  |
78 | 1.15 | A1 |
F atoms in plane wagging |
86 | 2.18 | B2 |
F atoms twisting |
92 | 0 | A2 |
F atoms scissoring  |
128 | 0.95 | A1 |
Wagging (all molecule, F at highier amplitute)  |
143 | 28.15 | B1 |
Cl atoms asymmetric stretch  |
243 | 4.14 | B2 |
Cls Symmetric stretch  |
257 | 1.40 | A1 |
Fs symmetric stretch  |
430 | 83.07 | A1 |
Fs assymetric stretch  |
430.28 | 66.87 | B2 |
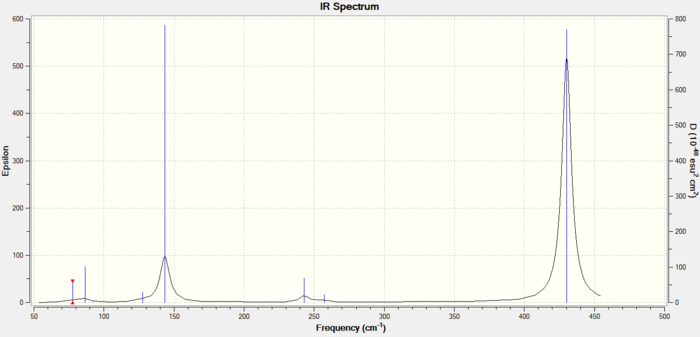
Replacing another Flourine with a Chlorine leads to a further decrease in all common frequencies. The minimum frequency is now at 78 cm-1, the wagging mode decreased from 231 cm-1 in XeF4 to 143 cm-1 in cis-XeF2Cl2, the Cl-Xe-F decreased from 255 cm-1 in XeF3Cl to 243 cm-1 (again as a result of raising the energy of all MOs by adding an extra Cl)
| Vibration | Frequency / cm-1 | Intensity / ε | Symmetry (D2h p.g.) |
Cl atoms in plane scissoring  |
56 | 1.56 | B2u |
Cl out of plane scissorin g |
66 | 1.09 | B3u |
F atoms rocking  |
117 | 0 | B3g |
F atoms in plane scissoring  |
141 | 1.41 | B1u |
Cls symmetric stretch  |
188 | 0 | Ag |
Fs out of plane scissoring  |
189 | 33.09 | B3u |
Cls asymmetric stretch  |
279 | 30.19 | B1u |
F symmetric stretch  |
419 | 0 | Ag |
F asymmetric stretch  |
505 | 92.87 | B2u |
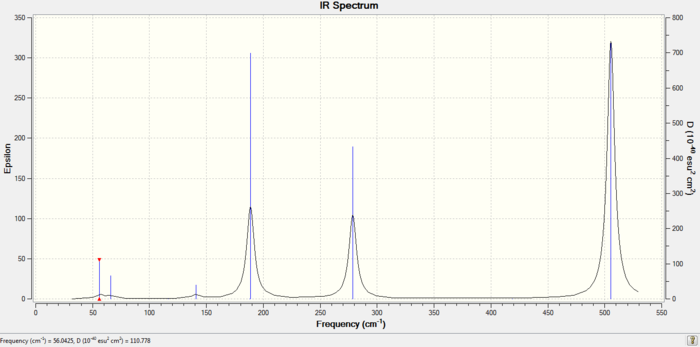
The trans-XeF2Cl2 has D2h symmetry and its vibrations can somewhat be compared with D4h XeF4. The F-Xe-F asymmetric stretch continues the trend and is even lower at 505 cm-1 compared to 514 in XeF3Cl and 524 cm-1 in XeF4; the same applies to the symmetric F-Xe-F stretch. The minimum bond stretching frequency is now the Cl-Xe-Cl at 188 cm-1, which should be populated at room temperature given the thermal energy available is about 220 cm-1.
Electronic structure and MOs analysis
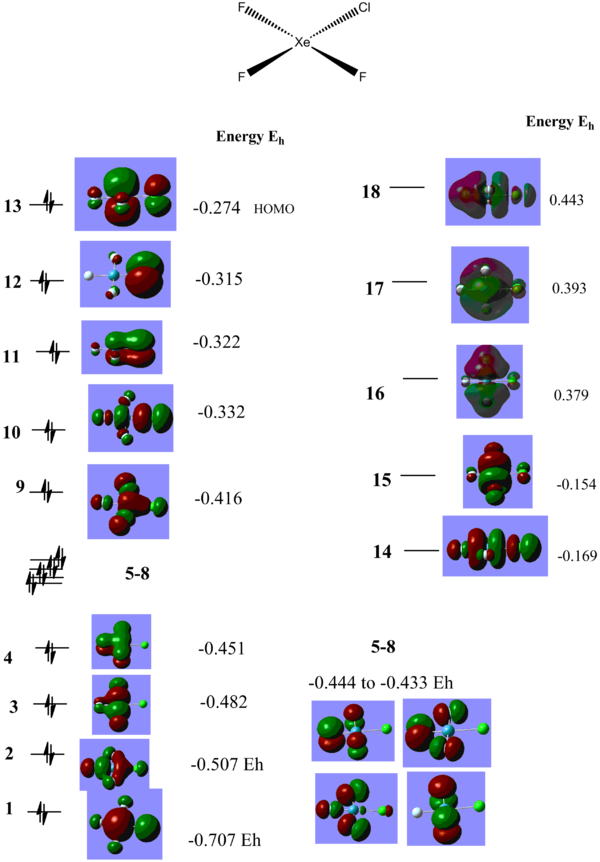
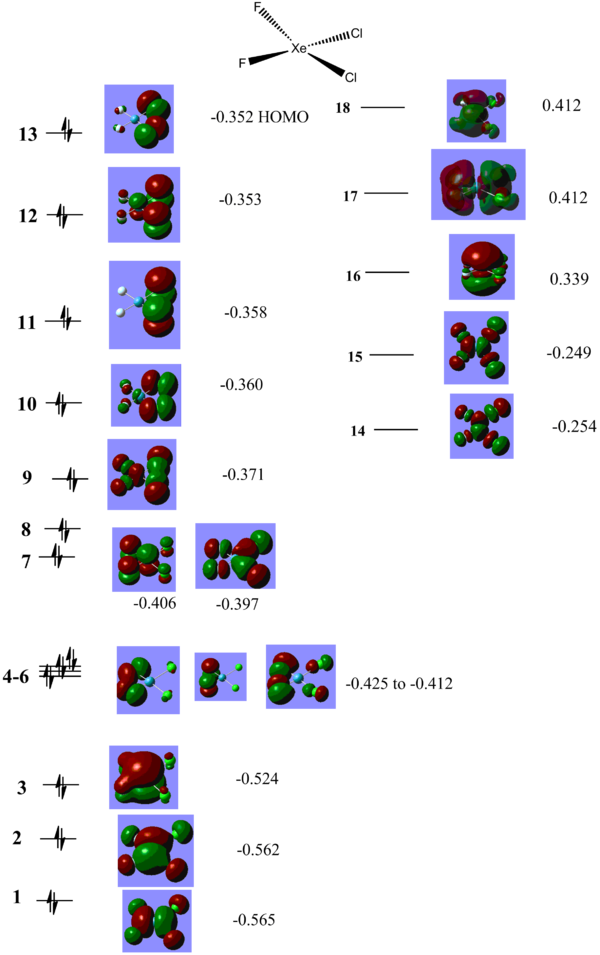
For XeF4 an MO diagram based on F4 SALC can be easily constructed. As can be seen from the diagram below, the prediected MOs correlate well with what is calculated.The diagram and computed MOs can be used as a reference point as we move on and study the other molecules MOs. XeF4_MOs DOI XeF3Cl MOs DOI cisXeF2Cl MOs DOI transXeF2Cl2 MOs DOI
 |
 |
 |
 |
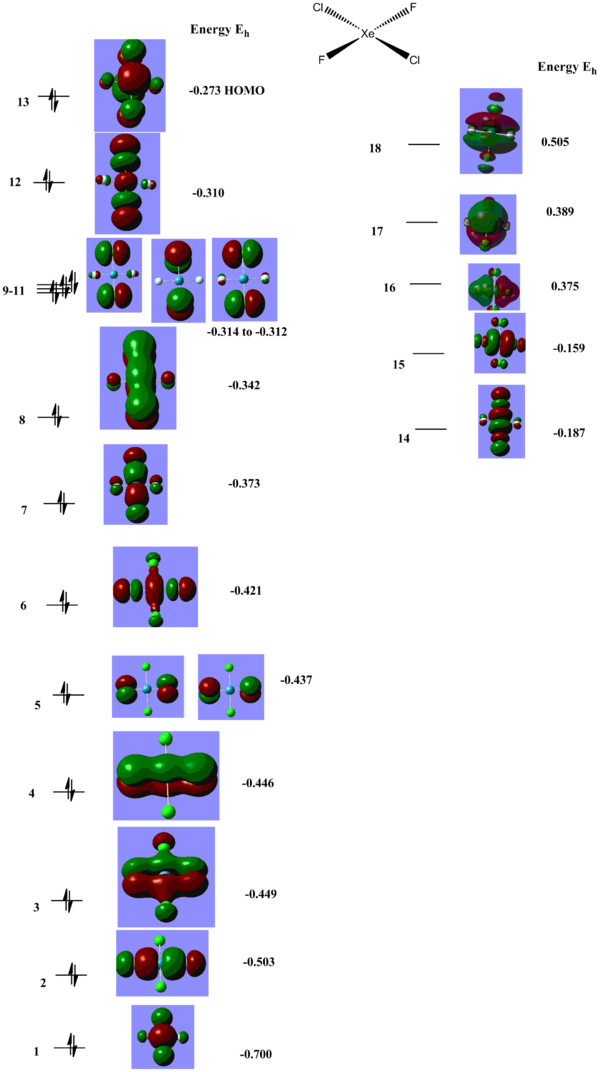From looking at the lowest energy MO in all 4 molecules (a1g in XeF4 and MO 1 in the rest of the molecules), it can be seen that it becomes higher in energy from going from XeF4 -0.724 Hartree, to XeF3Cl -0.707 Eh, to -0.700 Eh in trans XeF2Cl2 corresponding to adding more Cls, which has higher in energy AOs which leads to an increase in energy of all MOs.The cis XeF2Cl2 lowest energy MO is much more highier in energy, 0.565 Eh, due to the fact that the 1 MO has 3 nodes (cf. only one in the other three molecules), one which goes through the Xe atom. It can also be seen that the Cl contributes less to bonding than Fs and more to anti-bonding (for example in MO 1 in XeF3Cl).
Another interesting orbital to compare across the 4 structures is the 1a2g in XeF4, which is pi orbital, corresponding to a totally bonding interaction above and below the plane of the molecule, with a node in the plane of the molecule. It has an energy of -0.458 Hartree in XeF4, which only slightly increases in XeF3Cl to -0.451 Hartree. The corresponding MO in XeF3Cl is split into two separate MOs, one which includes the Fluorine atoms at -0.451 Hartree, and one interacting with the Cl atom, much highier in energy, MO 11 at -0.322 Hartree. This is higher in energy than the Fluorine lone pairs and even the Xe s based lone pair, MO 10 reflecting the much higher energy of the Cl p orbitals.
The HOMO of XeF4 corresponds to the Xe p based lone pair with an energy of -0.275 Hartree. It is a fully anti-bonding with respect to the F4 symmetry adapted fragment from the Fs lone pairs which should exhibit a slight trough speace bonding interaction. On XeF3Cl the HOMO is also the Xe p based lone pair (MO 13); the energy increased negligibly to -0.274 Hartree. Since this is not a bonding orbital it is expected that the presence of the Cl atom to have little impact on its energy. Since the orbital is fully anti-bonding with respect to the F4 SALC fragment orbital, the Cl atom contributes more to the anti bonding (represented by the increased size of the Cl lobes) since it is less electronegative. One noticeable difference is that the other Xe lone pair, which is the HOMO-1 in XeF4 with an energy of -0.386 Hartree, dropped by a significant amount in XeF3Cl, where it is MO 9 with an energy of -0.416 Hartree and it now below the Cl lone pair MO 12. This is due to less anti-boding interaction with only with 3 F SALC orbitals and actually forming a bonding interaction with an orbital of appropriate symmetry of Cl. As can be seen from the actual representation, there is in phase overlap between the Xe lone pair and the Cl atom.
The situation in the trans-XeF2Cl2 D2h molecule resembles the one in the XeF4 D4h molecule. The HOMO, MO 13, is the Xe p based lone pair with an energy of -0.273 Hartree (cf. -0.275 in XeF4 ) and the HOMO-1 is the Xe s based lone pair, MO 12, which is higher in energy (-0.310 vs. -0.386 Hartree in XeF4). The difference in energy is due to the fact that the MO is fully anti-bonding, and Cls have a bigger contribution to anti-bonding, hence putting in the Cls makes the MO more anti-bonding and higher in energy. The difference in energy is much less pronounced in the p based lone pair because p-p interactions are weaker leading to less destabilisation.
The situation is very different in cis-XeF2Cl2 where the HOMO is a Symmetry adapted MO from the two Cl lone pairs, MO 13. It has a relatively low energy of -0.352 Hartree, much lower in energy that the HOMO of the rest of the molecules (-0.273 to -0.275 Hartree). To compare, the Cl lone pairs in trans-XeF2Cl2 have an energy of - 0.314 to -0.312 Hartree (i.e. about 1 eV higher in energy). One explanation for this behaviour would be trans effect exhibited by the more electronegative F atoms, which bring down in energy the Cl orbitals. It can also be seen that the Xe based lone pairs are much lower in energy as they form much more MOs with both F2 and Cl2 fragments.
One of the first things noticeable by looking at the energies of the orbitals is that all of these molecules are predicted to be highly Lewis acidic as they have low lying empty orbitals in which they can accept electron density. Both the LUMO and LUMO+1 MOs are of low energy and can readily accept electrons. XeF4 LUMO and LUMO+1 are around -0.150 Hartree, for XeF3Cl they go down in energy to -0.169 and -0.154 Hartree, reflecting the lower stability of the molecule, which can theoretically react more easily with another F2 molecule to form the XeF4Cl2 or be subject to a SN2 type mechanism to replace one of the Cl with something more electronegative. The trend of decrease in energy of the LUMO and LUMO+1 follows to trans-XeF2Cl2, which are now -0.187 and -0.159 Hartree. For the case of cis-XeF2Cl2 the decrease is even more pronounced, -0.254 and -0.249 is now the energy of the LUMO and LUMO+1 which can be explained in terms of the trans effect exhibited by the F atoms since all these orbitals are a combination of Xe p symmetry adapted orbitals and F2 and Cl2 p symmetry adapted orbitals. Given the fact that all these molecules are Lewis acidic and also have readily accessible lone pairs it would be expected that they are very reactive. XeF4 readily reacts with moisture from the air to release Xe gas, HF and XeO3 and must be kept in anhydrous conditions. It is also used as decomposing agent for silicone rubber[10] for analyzing trace metal impurities.
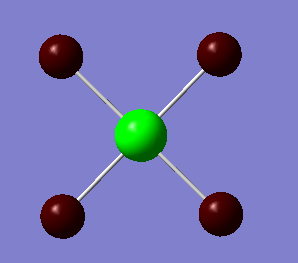
NBO analysis
| XeF4 | XeF3Cl | cis-XeF2Cl2 | trans-XeF2Cl2 |
|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
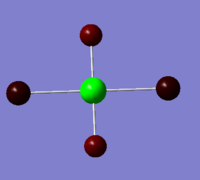
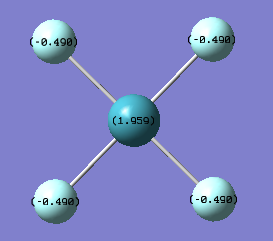
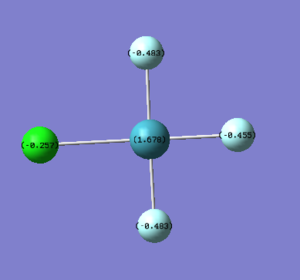
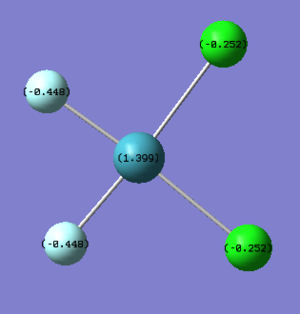
As expected the Xe atom is coloured bright green which indicates that it is highly positivly charged while the F and Cl atoms are coloured bright red which indicates that they are highly negatively charged. Substituting F atoms with less electronnegative Cl atoms has the effect of decreasing the positive charge at the Xe from 1.959 in XeF4 to 1.678 in XeF3Cl and 1.399 in cis-XeF2Cl2. The Pauling electronegativity of Xe is 2.6, for F is 4.0 and for Cl is 3.2. Thus as replacing the highly electronegative F atom with Cl atoms the bonds become less polarised.
By inspecting the .log file more information can be found. In the Bond orbital/ Coefficients/ Hybrids section information about the individual orbital components involved in bonding can be found.
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.99963) BD ( 1)Xe 1 - F 2
( 32.24%) 0.5678*Xe 1 s( 0.03%)p99.99( 99.97%)
-0.0001 -0.0162 0.0001 0.0000 -0.9993
-0.0329 0.0000 0.0000
( 67.76%) 0.8231* F 2 s( 2.59%)p37.54( 97.41%)
0.0000 -0.1606 0.0121 0.0000 0.0000
0.9869 0.0085 0.0000 0.0000
2. (1.99963) BD ( 1)Xe 1 - F 3
( 32.24%) 0.5678*Xe 1 s( 0.03%)p99.99( 99.97%)
-0.0001 -0.0162 -0.9993 -0.0329 0.0001
0.0000 0.0000 0.0000
( 67.76%) 0.8231* F 3 s( 2.59%)p37.54( 97.41%)
0.0000 -0.1606 0.0121 0.9869 0.0085
.......
43. (0.55243) BD*( 1)Xe 1 - F 2
( 67.76%) 0.8231*Xe 1 s( 0.03%)p99.99( 99.97%)
-0.0001 -0.0162 0.0001 0.0000 -0.9993
-0.0329 0.0000 0.0000
( 32.24%) -0.5678* F 2 s( 2.59%)p37.54( 97.41%)
0.0000 -0.1606 0.0121 0.0000 0.0000
0.9869 0.0085 0.0000 0.0000
44. (0.55243) BD*( 1)Xe 1 - F 3
( 67.76%) 0.8231*Xe 1 s( 0.03%)p99.99( 99.97%)
-0.0001 -0.0162 -0.9993 -0.0329 0.0001
0.0000 0.0000 0.0000
( 32.24%) -0.5678* F 3 s( 2.59%)p37.54( 97.41%)
0.0000 -0.1606 0.0121 0.9869 0.0085
0.0000 0.0000 0.0000 0.0000
The first occupancy is the bond between the Xe atom 1 and Fluorine 2 and 32.24% of the bond is contributed from the Xe orbitals which have a hybridisation of 0.03% s + 99.97% p, while 67.76% of the bond is contributed from the F orbitals which have a hybridisation of 2.59% s and 97.41% p. The second occupancy is the bond between Xe and Fluorine atom 3 and it exactly the same as the bonding between Xe and Fluorine 3.
Occupancies 3-6 are each of the four Fluorine core (CR) AOs which are 100% s hybridized.Occupancy 7 is the lone pair (LP) on the Xe atom which is 100% p hybridised.Occupancy 8 is the 2nd lone pair on the Xe atom as predicted by VSEPR but it hybridisation is 100%p hybridised. Occupancies 9 to 22 correspond to the F lone pairs, one s based (97.42%) lone pair for each F atom, the rest being p based. 23 to 42 are the Rydberg functions (higher energy orbitals like the Xe 6s) which arise because of using non basic basis set. These show very little occupancy and are of low interest.
43 is anti-bond (BD*) between the Xe and the Fluorine 2 and 67.76% of the bond is contributed from the Xe orbitals which have a hybridisation of 0.03% s and 99.97% p, while 32.24% of the bond is contributed from the F orbitals which have a hybridisation of 2.59% s and 97.41% p. The occupancy. The electron density is only 0.55 cf. 1.99 in the bonding (BD)occupancy. Occupancy 44 is an anti-bond(BD*)between Xe and Fluorine atom 3 and shows the same properties as 43.
The presence of these anti-bonds may due be a limitation of the method and basis set used or it may be Gaussian interpretation of breaking the octet rule, the fact that Xe has all its valencies satisfied and it doesn’t need to form any more bonds and the fact that its putting electrons in a bond with F atoms is considered to be anti-bonding.
There is no bond between the Xe atoms and the Fluorine atoms 4 and 5, only their lone pairs and Rydberg functions are present. This must be a limitation of the method and basis set used. For example the LANL2DZ basis set does not take into account the D orbitals of the Xe atoms which may have a pronounced effect in bonding.
Scrolling down, In the Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis quite a few interactions are seen between the Xe lone pairs and the Rydgberd orbitals on the F atoms, between the F lone pairs and the Xe atom Rydberg orbitals. There are also interactions between the Xe-F BD and Xe-F BD*. Most of these interactions are of the order of 2 to 15 kcal/mol. At the bottom we find the missing bonds between the Xe and Fluorine 4 and 5. These are listed as an interaction between one of F lone pairs and the trans-Xe-F BD*, each bond is 141 kcal/mol. This is probably a limitation of the method/basis set used and further research is needed to determine why the other two bonds are seen as secondary interactions.
Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis
Threshold for printing: 0.50 kcal/mol
(Intermolecular threshold: 0.05 kcal/mol)
E(2) E(j)-E(i) F(i,j)
Donor NBO (i) Acceptor NBO (j) kcal/mol a.u. a.u.
===================================================================================================
within unit 1
1. BD ( 1)Xe 1 - F 2 / 43. BD*( 1)Xe 1 - F 2 6.60 0.31 0.047
2. BD ( 1)Xe 1 - F 3 / 44. BD*( 1)Xe 1 - F 3 6.60 0.31 0.047
8. LP ( 2)Xe 1 / 27. RY*( 1) F 2 1.06 2.26 0.044
8. LP ( 2)Xe 1 / 31. RY*( 1) F 3 1.06 2.26 0.044
8. LP ( 2)Xe 1 / 43. BD*( 1)Xe 1 - F 2 4.03 0.65 0.054
8. LP ( 2)Xe 1 / 44. BD*( 1)Xe 1 - F 3 4.03 0.65 0.054
11. LP ( 3) F 2 / 44. BD*( 1)Xe 1 - F 3 8.05 0.12 0.033
14. LP ( 3) F 3 / 43. BD*( 1)Xe 1 - F 2 8.05 0.12 0.033
...............................
18. LP ( 4) F 4 / 43. BD*( 1)Xe 1 - F 2 140.72 0.17 0.139
22. LP ( 4) F 5 / 44. BD*( 1)Xe 1 - F 3 140.72 0.17 0.139
Next in the .log file is the NBO summary:
Natural Bond Orbitals (Summary):
Principal Delocalizations
NBO Occupancy Energy (geminal,vicinal,remote)
====================================================================================
Molecular unit 1 (F2Xe)
1. BD ( 1)Xe 1 - F 2 1.99963 -0.62107 43(g),35(r)
2. BD ( 1)Xe 1 - F 3 1.99963 -0.62107 44(g),39(r)
3. CR ( 1) F 2 2.00000 -24.53774
4. CR ( 1) F 3 2.00000 -24.53774
7. LP ( 1)Xe 1 1.99983 -0.52030
8. LP ( 2)Xe 1 1.99692 -0.96389 43(g),44(g),35(r),39(r)
27(v),31(v)
9. LP ( 1) F 2 1.99995 -0.43583
10. LP ( 2) F 2 1.99946 -1.30476
11. LP ( 3) F 2 1.95572 -0.43368 44(v),40(r)
12. LP ( 1) F 3 1.99995 -0.43583
13. LP ( 2) F 3 1.99946 -1.30476
14. LP ( 3) F 3 1.95572 -0.43368 43(v),36(r)
23. RY*( 1)Xe 1 0.00223 1.08382
24. RY*( 2)Xe 1 0.00220 0.43805
25. RY*( 3)Xe 1 0.00150 12.47738
26. RY*( 4)Xe 1 0.00013 0.33908
27. RY*( 1) F 2 0.00130 1.29388
28. RY*( 2) F 2 0.00027 0.81869
29. RY*( 3) F 2 0.00006 0.78357
30. RY*( 4) F 2 0.00001 1.08029
31. RY*( 1) F 3 0.00130 1.29388
32. RY*( 2) F 3 0.00027 0.81869
33. RY*( 3) F 3 0.00006 0.78357
34. RY*( 4) F 3 0.00001 1.08029
43. BD*( 1)Xe 1 - F 2 0.55243 -0.31081 44(g),25(g),23(g),27(g)
44. BD*( 1)Xe 1 - F 3 0.55243 -0.31081 43(g),25(g),23(g),31(g)
-------------------------------
Total Lewis 69.90626 ( 98.4312%)
Valence non-Lewis 1.10487 ( 1.5557%)
Rydberg non-Lewis 0.00934 ( 0.0131%)
-------------------------------
Total unit 1 71.02046 (100.0000%)
Charge unit 1 0.97954
Interestingly the Xe-F anti-bond (BD*) is seen as a favorable interaction with in which delocalisation around the whole molecule happens.
For the case of XeF3Cl the first occupancy is the bond (BD) between the Xe atom 1 and the Fluorine atoms 2 and 33.29% of the bond is contributed from the Xe orbitals, which have a hybridization of 0.02%s+99.98%p, while 66.71% of the bond comes from the F orbitals which have a hybridization of 2.64%s+97.36%p.
The second occupancy is the bond (BD) between the Xe atom 1 and the Chlorine atom 5 and 49.17% of the bond is contributed from the Xe orbitals, which have a hybridisation of 0.26%s+99.74%p, while 50.83% of the bond comes from the Cl orbitals which have a hybridisation of 0.59%s+99.41%p.
By replacing a F atom with a Cl one, the bonding is expected to change as the Cl is less electronegative and is a period down (thus with more diffuse orbitals). Thus, the bond contribution changes from 66.71% contribution in from F to 50.83% when Cl and from 2.59%s character to 0.59%, in line with the fact that s-p gap increases when going down the group.
Occupancies 3 to 41 are the lone pairs and the Rydberg orbitals, similar to the XeF4 case.
The 42nd occupancy is an anti-bond (BD*) between the Xe and the Fluorine 2 and 66.71% of the bond is contributed from the Xe orbitals, which have a hybridisation of 0.02%s+99.98%p, while 33.29% of the bond comes from the F orbitals which have a hybridisation of 2.64%s+97.36%p. The 43rd occupancy is an anti-bond(BD*) between the Xe atom 1 and the Chlorine atom 5 and of the bond is 50.83% contributed from the Xe orbitals, which have a hybridisation of 0.26%s+99.74%p, while49.17% of the bond comes from the Cl orbitals which have a hybridisation of 0.59%s+99.41%p.
In the Second Order Perturbation Theory Analysis of Fock Matrix the two missing bonds are found listed as secondary interactions between the lone pairs on the F atoms and the Xe-F and Xe-Cl BD*. The Fluorine labelled 3 (trans to Cl) has a bond energy of 131 kcal/mol and the other F has a slightly higher bond energy of 141 kcal/mol. In the cis-XeF2Cl2, the first occupancy is the bond (BD) between the Xe atom 1 and the Chlorine atom 4 and 50.02% of the bond is contributed from the Xe orbitals, which have a hybridisation of 0.32%s+99.68%p, while 49.98% of the bond comes from the Cl orbitals which have a hybridisation of 0.61%s+99.39%p.
The 2nd occupancy is bond(BD) ) between the Xe atom 1 and the Chlorine atom 5, identical with the other Xe-Cl bond. Analogous to XeF4 and XeF3Cl, the next occupancies are the lone pairs and Rygberg AOs.
Occupancies 41 and 42 are the Xe-Cl anti-bond(BD*), and 49.98% of the bond is contributed from the Xe orbitals, which have a hybridisation of 0.32%s+99.68%p, while 50.02% of the bond comes from the Cl orbitals which have a hybridisation of 0.61%s+99.39%p.
The Xe-F bonds are again listed in the Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis as F lone pairs donating into the Xe-Cl BD*, and have an energy of 134 kcal/mol comparable to the Xe-F bond trans to Cl in XeF3Cl (131 kcal/mol).
In the trans-XeF2Cl2, the first occupancy is the bond between the Xe atom 1 and Fluorine 3 and 33.88% of the bond is contributed from the Xe orbitals which have a hybridisation of 0.02% s + 99.98% p, while 66.12% of the bond is contributed from the F orbitals which have a hybridisation of 2.61% s and 97.39% p.
The second occupancy is the bond between Xe and Fluorine atom 3 and it exactly the same as the bonding between Xe and Fluorine 3.
The second occupancy is the bond (BD) between the Xe atom 1 and the Chlorine atom 5 and 50.00% of the bond is contributed from the Xe orbitals, which have a hybridisation of 0.26%s+99.74%p, while 50.00% of the bond comes from the Cl orbitals which have a hybridisation of 0.26%s+99.74%p.
Occupancies 3 to 40 as previously are the lone pairs of the Xe, F and Cl atoms and at the bottom, occupancies 41 is the Xe(1)-F(3) anti-bond (BD*) in which Xe orbitals contribute 66.12% and F orbitals 33.88% while the hybridasation remains the same as in the bonding Xe-F. Occupancy 42 is the anti-bond (BD*) Xe(1)-Cl(5), with 50/50 contributions from each atom orbitals.
XeF4 square planar or tetrahedral
VSEPR predicts that the XeF4 molecule will be square planar with the two lone pairs occupying an axial position where they are 180o to each other. The energy of each isomer can be calculated and compared. The tetrahedral XeF4 was constructed stating from carbon tetrahedral, manually editing of the.gjf file to add the Xe. The geometry was fixed to the Td point group and Tolerance was set to very tight. A DFT-B3LYP/LANL2DZ geometry optimisation was performed on the structure, a summary of which can be found below:
Filename = H:\3rdyearlab\mini project\new and last attempt\xef4 tetraheral\XeF4 tetrahedral geom opt with td set and ultrafine.log XeF4 tetrahedral geom opt set to td and ultra tight File Name = XeF4 tetrahedral geom opt with td set and ultrafine File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2DZ Charge = 0 Spin = Singlet E(RB3LYP) = -414.5067 a.u. RMS Gradient Norm = 0.00019724 a.u. Imaginary Freq = Dipole Moment = 0.0069 Debye Point Group = Td Job cpu time: 1 minutes 59.0 seconds.
As can be seen, the square planar arrangement is more stable by about 0.17 Hartree or approx 4.6eV, in good agreement with the 5eV value found in literature[11]
Is trans-XeF2Cl2 more stable than cis?
The absolute energies of the trans and cis isomers can be readily compared. Thus the trans isomer is 0.22 eV (21 kJ/mol) more stable than the cis.
References
- ↑ Kawaguchi, Kentarou, Journal of Chemical Physics, 1992 , vol. 96, p. 3411 - 3415 , DOI: 10.1063/1.461942.
- ↑ Kawaguchi, Kentarou; Butler, J. E.; Yamada, Chikashi; Bauer, S. H.; Minowa, Tatsuya; et al. Journal of Chemical Physics, 1987 , vol. 87, p. 2438 - 2441 10.1063/1.453135.
- ↑ Schwenke, David W. Journal of Physical Chemistry, 1996 , vol. 100, p. 2867 - 2884 DOI: 10.1021/jp9525447.
- ↑ Edard F., Tronc M., Chemical Physics Letters Volume 167, Issue 6, 13 April 1990, Pages 602-606
- ↑ Blixt J., Glaser J., Mink M., Persson I., Persson N., Journal of the American Chemical Society,1995 ,vol. 117,p. 5089 - 5104
- ↑ M. Y. Darensbourg and D. J. Darensbourg, J. Chem. Ed. 1970, 47, 33.
- ↑ G. Hogarth, T. Norman, Inorganica Chimica Acta, 1997, 254, 167-171
- ↑ Valery K., Namig S., Pirkuliev V., Zefirov S.,Russian Chemical Reviews, Vol..70, 2001, 3, 231-242 doi:10.1070/RC2001v070n03ABEH000626
- ↑ Grant, Daniel J.; Wang, Tsang-Hsiu; Dixon, David A.; Christe, Karl O. Inorganic Chemistry, 2010 , vol. 49, p. 261 - 270
- ↑ Rigin, V., Nikolaj K., Vassili V., Analytica Chimica Acta, 340, 1970, 1–3, doi:10.1016/S0003-2670(96)00563-6
- ↑ Buerger, H.; Ma, S.; Breidung, J.; Thiel, W. Journal of Chemical Physics, 1996 , vol. 104, p. 4945 - 4953 DOI: 10.1063/1.471266.