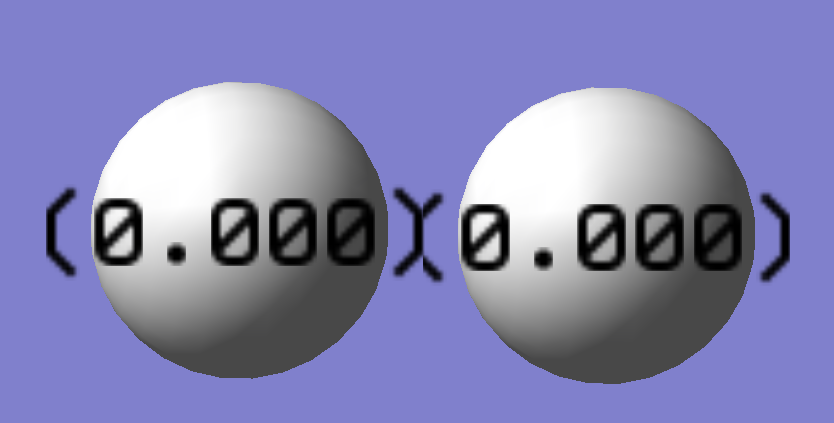User:Ce1116
NH3 Molecule
molecule name: NH3
calculation method: RB3LYP
basis set: 6-31G(d,p)
final energy in atomic units: -56.55776873
point group: C3V
bond distance: 1.01798 au
Bond angle (H-N-H): 105.741 degrees
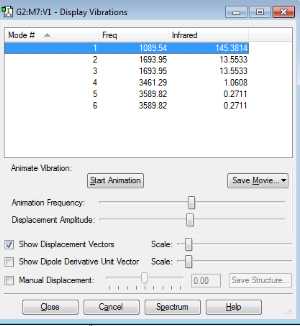
The below table is for optimized NH3.This is shown by the fact that the maximum force is less than 0.00045 au, the maximum displacement is also less than 0.0003 which is required for optimisation to be complete.
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES Predicted change in Energy=-5.986292D-10
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
File:CATHYEAGLE NH3 MOLECULE1.LOG
test molecule |
The optimisation file is linked to here
The table above shows the different vibrational modes in an ammonia molecule. We would expect there to be 6 different modes due to the 3N-6 rule, however, there are only 4 different distant modes. There are 2 sets of 2 degenerate modes 2/3 and 5/6. Modes 1,2 and 3 are bending modes whereas 4,5 and 6 are stretching modes. Mode 4 is highly symmetric and mode 1 is known as the "umbrella" mode. I would expect to see four different bands in an experimental spectrum for gaseous ammonia. The modes 5 and 6 show very low intensities due to the nature of the bend which produces a very small change in dipole moment in comparison to mode 1 which show a large change in dipole moment, therefore, a large peak.
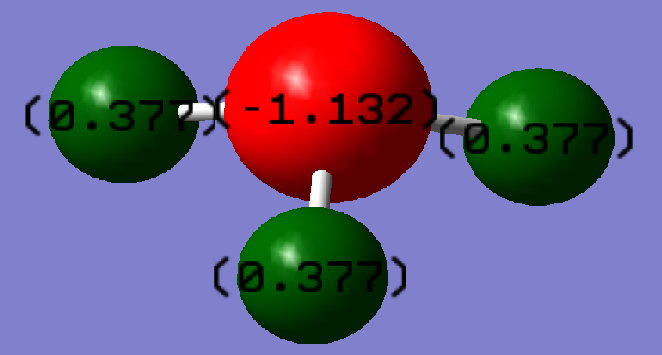
The charge distribution throughout the molecule is shown in the illustration above. The nitrogen atom is more negative than any of the hydrogens in NH3. This is expected since nitrogen is more electronegative than hydrogen so tends to attract electrons more easily.
N2 Molecule
molecule name: N2
calculation method: RB3LYP
basis set: 6-31G(d,p)
final energy in atomic units: -109.52412868
point group: Dinfh
bond distance: 1.10550 au
An N2 molecule is illustrated below: File:CATHYEAGLEN2OPT.LOG
test molecule |
The optimisation file is linked to here
The below table is for optimised N2, this is shown by the fact that the maximum force is less than 0.00045 au, the maximum displacement is also less than 0.0003 which is required for optimisation to be complete.
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES Predicted change in Energy=-3.401057D-13
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
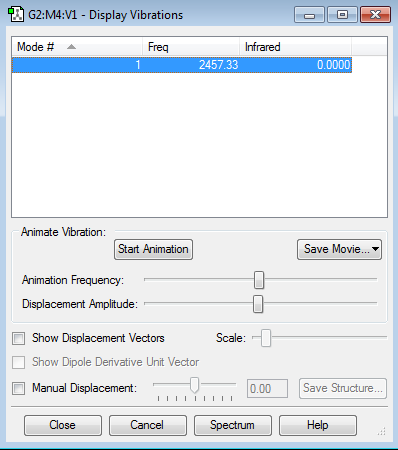
The table above shows the vibrational mode in an N2 molecule. There is only one mode which is a bond stretch which is expected due to the 3N-5 rule for linear molecules. The vibrational mode has an intensity of zero since the vibration produces no change in dipole moment which is responsible for the intensity of the vibration on the spectrum.
The image below shows the charge distribution in a nitrogen molecule by colour:
As expected the charge is distributed symmetrically in the nitrogen molecule since it is homonuclear so there is no difference in electronegativity between the two atoms.
H2 Molecule
molecule name: H2
calculation method: RB3LYP
basis set: 6-31G(d,p)
final energy in atomic units: -1.17853936
point group: Dinfh
bond distance: 0.74279
The animation below shows an H2 molecule.
File:CATHYEAGLEH2MOLECULE2.LOG The optimisation file is linked to here
test molecule |
The below table is for optimised H2, this is shown by the fact that the maximum force is less than 0.00045 au, the maximum displacement is also less than 0.0003 which is required for optimisation to be complete.
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES Predicted change in Energy=-1.164080D-13
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
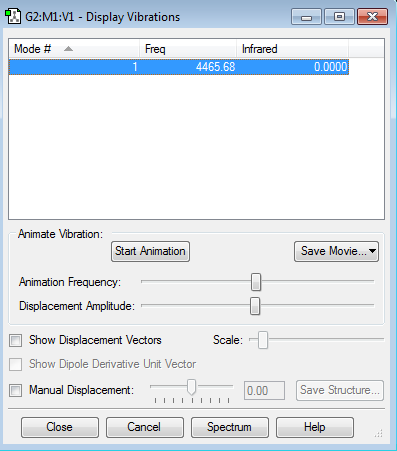
The table above shows one vibrational mode, this is to be expected since the molecule is composed of only two atoms in a linear formation so using the 3N-5 rule we predict only one vibrational mode. The intensity of the vibration is zero since there is no change in dipole moment when the bond stretches.
The electrons are evenly distributed in this molecule since there is no electronegativity difference between the H atoms.
Reaction Energies
N2 + H2 -> 2NH3 E(NH3)= -56.55776873au = -148836.2335 kJ/mol
2*E(NH3)= -297672.467 kJ/mol
E(N2)= -109.52412868au = -288221.3913 kJ/mol
E(H2)= -1.17853936au = -3101.419668 kJ/mol
3*E(H2)= -9304.258105 kJ/mol
change in E= 2*E(NH3)-[E(N2)+3*E(H2)]= -146.817595 kJ/mol
The enthalpy of the reaction found in literature is -92 kJ/mol (http://www.chemguide.co.uk/physical/equilibria/haber.html , data accessed: 24/02/17). The large difference in the values here may be due to the computer programme using purely theoretical reasoning and calculations to find the energy of the molecules rather than reality, where the conditions are very different with other molecules involved.
The products are more stable than the reactants which can be predicted by the fact that the enthalpy change is negative so the products are formed more readily.
Cl2 Molecule
molecular name: Cl2
calculation method: RB3LYP
basis set: 6-31G(d,p)
final energy in atomic units: -920.34987886
point group: Dinfh
bond distance: 2.04174
An optimised rotatable image of Cl2 is given below:
The optimisation file is linked to here
test molecule |
The below table is for optimised Cl2, this is shown by the fact that the maximum force is less than 0.00045 au, the maximum displacement is also less than 0.0003 which is required for optimisation to be complete.
Item Value Threshold Converged? Maximum Force 0.000043 0.000450 YES RMS Force 0.000043 0.000300 YES Maximum Displacement 0.000121 0.001800 YES RMS Displacement 0.000172 0.001200 YES Predicted change in Energy=-5.277187D-09
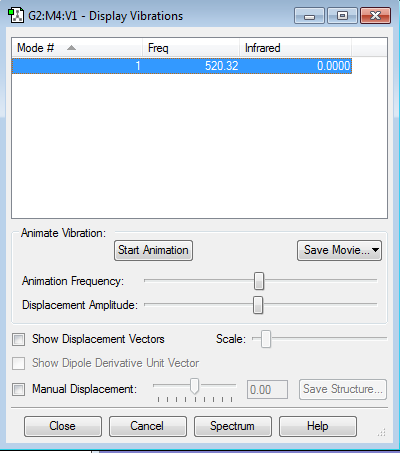
The vibrational mode of Cl2 is shown in the table below. There is only one mode due to the 3N-5 rule for linear molecules. Additionally, the intensity of the peak is zero since there is no change in dipole moment during the molecular vibration.
The charge distribution of a chlorine molecule is represented below. The charge is evenly distributed between the two atoms because they are identical and uncharged.
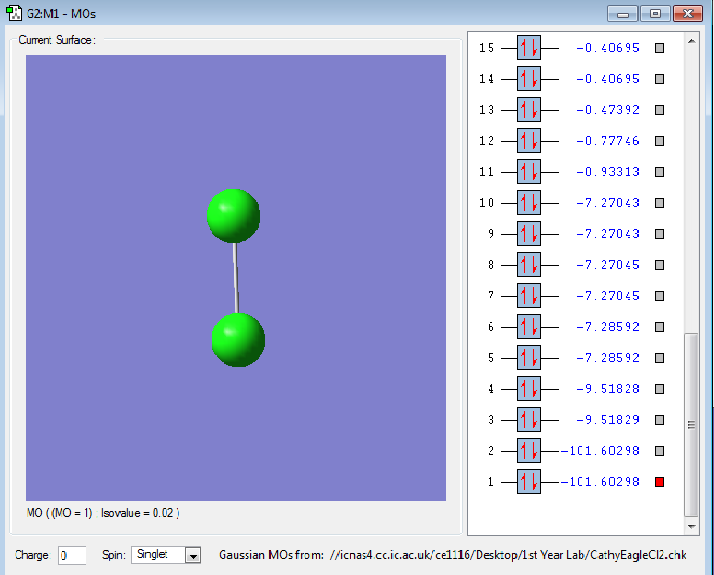
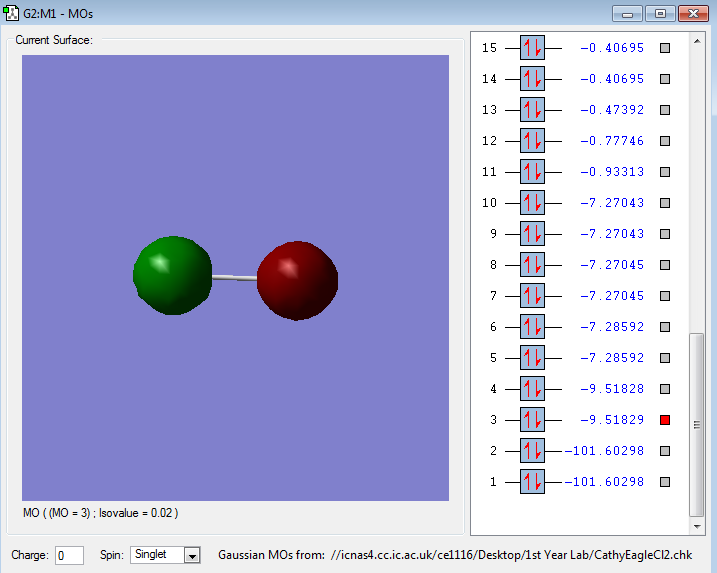
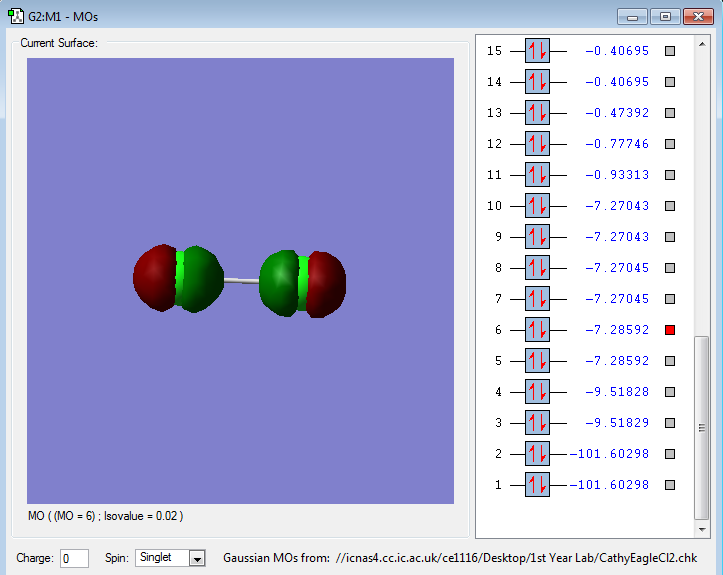
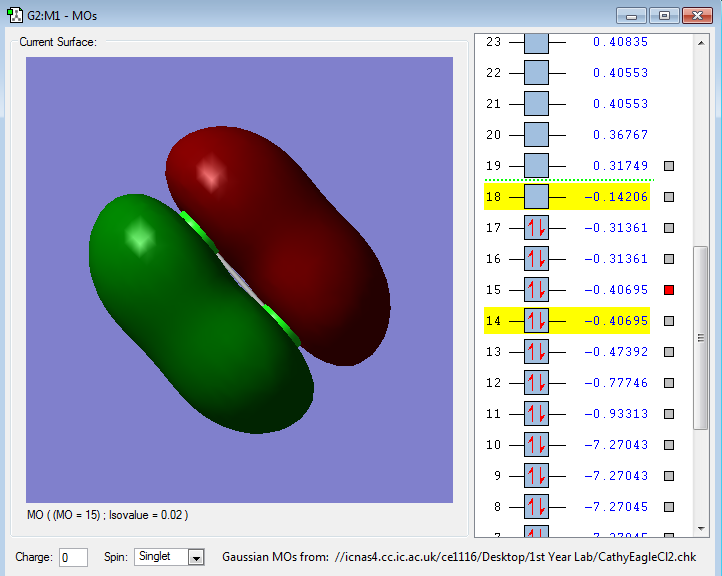
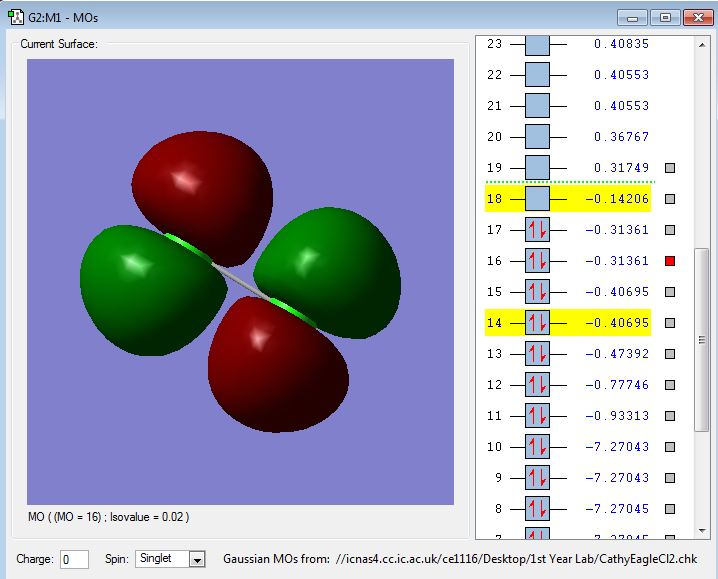
The following images are representations of molecular orbitals in a chlorine molecule.
The diagram of the molecule above shows the 1s orbitals in each Cl atom which are non bonding.
The diagram of the Cl2 molecule above shows the 2s orbitals, these are core so not involved in bonding.
The molecular orbitals shown in the diagram above show a sigma bond between the two 2pz atomic orbitals in each Cl as they are in phase and bonding.
The molecular orbitals in the illustration above show the 2px pi bonding orbital which is higher in energy than the sigma bond.
The molecular orbitals in this illustration show the pi antibonding orbitals which the out-of-phase interaction of the 2px orbitals causes.