User:Ap5817
NH3 molecule
NH3 calculations
Calculation method:RB3LYP
Basis Set = 6-31G(d,p)
Final Energy: E(RB3LYP) = -56.557768 a.u.
Bond length:1.01789 Å
Bond angle: 105.741 °C
Point Group: C3v
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
test molecule |
Media:ADRIAN_POPESCU_PHUNT_NH3_OPTF_POP.LOG
Vibration analysis of NH3
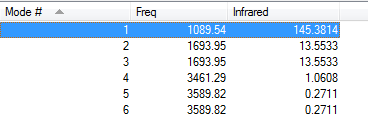
Vibrational modes
Number of vibrational modes: 6
Number of degenerate modes: 4 (2 pairs of degenerate vibrational modes )
Number of bending motions: 3
Number of stretching motions: 3
The most symmetric vibrational mode: mode #4
The umbrella mode: mode #1
Number of bands expected to be seen in an experimental spectrum of gaseous ammonia: 5
Charge Analysis
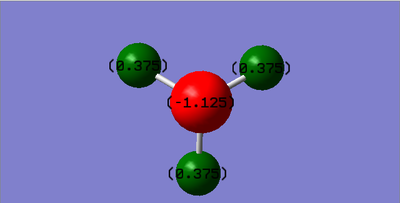
Charge on the N atom: -1.125
Charge on the H atom: 0.375
As Nitrogen has an electronegativity value of 3.04, which is significantly larger than the one of Hidrogen (2.2), it is expected that on the Nitrogen there will be a negative charge and on Hidrogen a possitive charge.
Reactivity of the Haber-Bosch process
Analysis of H2
Calculation method: RB3LYP
Basis Set = 6-31G(d,p)
Final Energy: E(RB3LYP) = -1.1785393 a.u.
Bond length: 0.7428 Å
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000005 0.001800 YES RMS Displacement 0.000007 0.001200 YES
Vibrational mode Frequency Infrared #1 4465.6 0.0000
There are no vibrational modes with negative frequencies
Analysis of N2
Calculation method: RB3LYP
Basis Set = 6-31G(d,p)
Final Energy: E(RB3LYP) = -109.5241268 a.u.
Bond length: 1.1055 Å
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
Vibrational mode Frequency Infrared #1 2457.33 0.0000
There are no vibrational modes with negative frequencies.
Calculation of the energy of the Haber-Bosch process
N2 + 3H2 -> 2NH3
E(NH3)= -56.557768 a.u.
2*E(NH3)= -113.115536 a.u.
E(N2)= -109.5251268 a.u.
E(H2)= -1.1785393 a.u.
3*E(H2)= -3.5359617 a.u.
ΔE= 2*E(NH3) - [E(N2) + 3*E(H2)] = -145.57 kj/mol
As the reaction is exothermic, the ammonia product is more stable than the gaseous reactants.
The literature value of the Haber-Bosch process is ΔE= -45.8 kj/mol [1], which indicates that the process is still exothermic, but the amount of energy released is significantly smaller.
Analysis of Cl2
General Analysis
Calculation method: RB3LYP
Basis Set = 6-31G(d,p)
Final Energy: E(RB3LYP) = -920.3498788 a.u.
Bond length: 2.0417 Å
Vibrational Analysis
Item Value Threshold Converged? Maximum Force 0.000043 0.000450 YES RMS Force 0.000043 0.000300 YES Maximum Displacement 0.000121 0.001800 YES RMS Displacement 0.000172 0.001200 YES
Vibrational mode Frequency Infrared #1 520.32 0.0000
There are no vibrational modes with negative frequencies
Charge Analysis
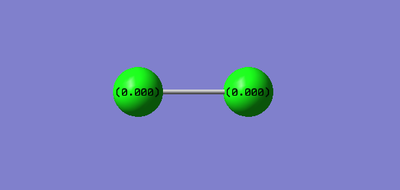
As the Cl2 molecule is made up of identical Cl atoms, the bond between them will be 100% covalent, the electrons that form the sigma bond are equally shared between the Cl atoms, so the charge on each Cl atom is zero.
Molecular orbitals Analysis

The 2σg bonding orbital is deep in energy, occupied, and corresponds to the bonding orbital formed by the 2s AOs of the Cl atoms.
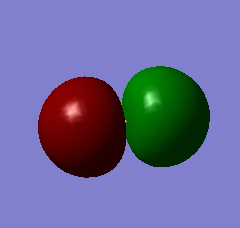
The 2σu* orbital is higher in energy than the 2σg orbital, is occupied, and corresponds to the antibonding orbital formed by the 2s AOs of the Cl atoms.

The 3σg orbital is deep in energy, occupied, and corresponds to the bonding orbital formed by the 3px AOs of the Cl atoms.
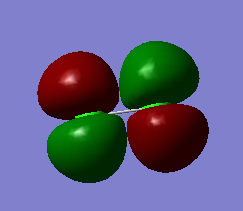
The 1πg* orbital is high in energy, and is the HOMO (Highest Occupied Molecular Orbital). It corresponds to the antibonding orbital formed by the 3py (or 3pz, as the orbitals are degenerate) AOs of the Cl atoms.

The 3σu* orbital is high in energy, and is the LUMO (Lowest Unoccupied Molecular Orbital). It corresponds to the antibonding orbital formed by the 3px AOs of the Cl atoms.
