User:Am3912

EX₃ section

Parameter	BH3	GaBr3	BBr3
r(E-X) Å	1.19	2.35	1.93
θ(X-E-X) degrees(º)	120.0	120.0	120.0

BH₃

B3LYP/3-21G level

Optimisation log file here

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000217 0.000450 YES RMS Force 0.000105 0.000300 YES Maximum Displacement 0.000919 0.001800 YES RMS Displacement 0.000441 0.001200 YES Predicted change in Energy=-1.635270D-07 Optimization completed.	Optimised Borane Molecule

B3LYP/6.21G(d,p) level

Optimisation log file here

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000203 0.000450 YES RMS Force 0.000098 0.000300 YES Maximum Displacement 0.000867 0.001800 YES RMS Displacement 0.000415 0.001200 YES Predicted change in Energy=-1.436186D-07 Optimization completed.	Optimised Borane Molecule

GaBr₃ B3LYP/LANL2DZ

Optimization log file DOI:10042/143660

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000003 0.001800 YES RMS Displacement 0.000002 0.001200 YES Predicted change in Energy=-1.307764D-12 Optimization completed.	Optimised GaBr3

BBr₃ B3LYP/6-31G(d,p)LANL2DZ

Optimization log file DOI:10042/143661

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000011 0.000450 YES RMS Force 0.000007 0.000300 YES Maximum Displacement 0.000047 0.001800 YES RMS Displacement 0.000031 0.001200 YES Predicted change in Energy=-6.887156D-10 Optimization completed.	Optimised BBr3

BBr₃ D_3h Symmetry Imposed B3LYP/6-31G(d,p)LANL2DZ

Optimization log file DOI:10042/143667

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000008 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.000035 0.001800 YES RMS Displacement 0.000023 0.001200 YES Predicted change in Energy=-3.932635D-10 Optimization completed.	Optimised BBr3

Questions

Each of the molecules are EX₃, with a trigonal planar structure and 120 degree bond angles, and as the central atom for each is in group 13, they are all slightly electron deficient, with an incomplete octet. One would expect that moving through the compounds, from BH₃ to BBr₃ and to GaBr₃, the bond length would increase if we use a purely atomic radii based argument. This is obviously not the whole description and ignores any contributions non-covalent. If we look at BH₃, we see a very accurate covalent description, with the predicted bond length of 115 pm, very similar to our calculated value of 119 pm. Bromine is an electronegative atom and hence gives an ionic contribution to the now polarised bond also. This leads to our calculate value of 193 pm being slightly away from the suggested 204 pm bond length. As stated before, the molecules are electron deficient, and bromine can donate electron density from its lone pairs in order to stabilise the compound. This pi donation into the empty sp₂ orbital on B and Ga gives a small amount of double bond character, and hence reduces the bond distance, as seen. Hydrogen on the other hand has no lone pairs of electrons and therefore cannot stabilise the central atom like bromine can. Boron is a better electron acceptor than gallium is and is therefore stabilised greater than gallium is, as is shown by the greater bond length in GaBr₃, which appears to have very little pi stabilisation at all, with the predicted covalent radius of 238 pm matching up with the calculate radius of 235 pm. This can be explained by the difference in size of the orbitals on gallium and bromine and therefore ineffective overlapping being present, so pi overlap is very minimal.¹

A bond is the attraction between 2 or more different atoms which holds them together in a definable arrangement. They are present in various different forms, from strictly covalent bonds, as seen above in BH₃ to ionic interactions, such as those between sodium and chlorine ions in NaCl, to metallic bonds where delocalised electrons hold together a lattice of metallic atoms, where the oppositely charged particles stronly attract one another. Other less strictly defined as bonds would be hydrogen bonds, which are present between hydrogen and electronegatively charged elements such as oxygen. Hydrogen bonding can be relatively strong when between hydrogen and fluorine. Ionic and metallic bonds are typical strong, requiring large amounts of energy to overcome. Covalent bonds come in various forms also, ranging from some of the strongest bonds such as the nitrogen-nitrogen triple bond in N₂, with a bond dissociation energy of 945 kJ/mol, to weak 3/4-centre-2-electron bonds as seen in some bridging systems. A medium strength bond would be something like a simple carbon-carbon bond present in organic molecules, with a dissociation energy of around 350 kJ/mol. Bonds between halogens are some of the weakest singular covalent bonds, with a strong repulsion between lone pairs of electrons on each halogen giving a large destabilising effect. The bond between two iodine atoms has a dissociation energy of just 151 kJ/mol.

Gaussview doesn't always draw bonds which are still in fact present as bonds, working purely on a distance basis of pre-calculated values, so if the bond is just weak, gauss view may not show it if it's not within the required distance. An example where this is the case is the bridging boron-hydrogen bond in diborane, which gaussian assumes is the same as a standard B-H bond as seen above.

BH₃ B3LYP/6.21G(d,p)

Frequency file here

Summary Data	Low modes
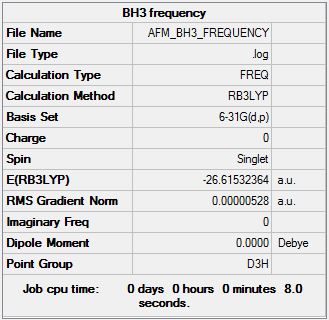	Low frequencies --- -14.4997 -14.4956 -10.7948 0.0013 0.0169 0.3459 Low frequencies --- 1162.9510 1213.1232 1213.1234

Wavenumber/cm-1	Intensity	IR active?	Type
1163	93	Yes	Bend (Wag)
1213	14	Yes (Weak)	Bend (Scissoring + Rocking)
1213	14	Yes (Weak)	Bend (Scissoring)
2583	0	No	Stretch (Symmetric)
2716	126	Yes	Stretch (Anti symmetric)
2716	126	Yes	Stretch (Anti symmetric)

Questions

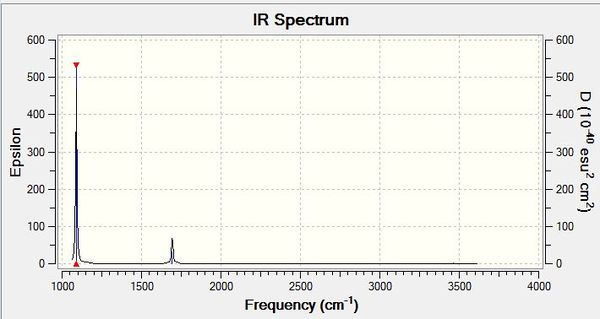
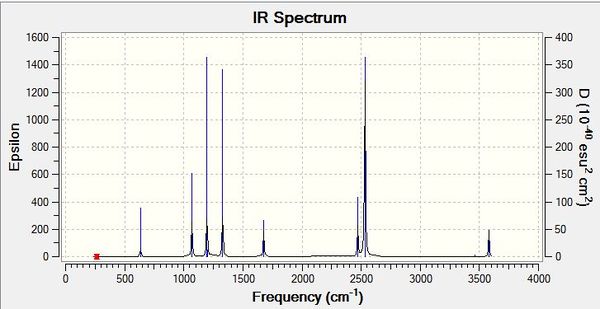
As can be seen in the table above, there are 6 different vibrations present in the molecule, however there are not 6 peaks in the spectrum. This follows from non-linear molecules possessing 3N-6 vibrational modes of freedom, where N is the number of atoms present. Not all vibrations are IR active and have to show a change in dipole moment in order to show up on the spectrums. The symmetric stretch at 2583 cm ^-1 in this case is not IR active, with no change in dipole moment and hence shows no peak on the spectrum. Also, some of the vibrations are degenerate and hence are shown overlapping in the spectrum.

GaBr₃ Frequency B3LYP/LANL2DZ

Frequency log file DOI:10042/143671

Summary Data	Low modes
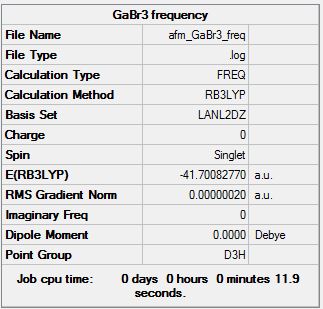	Low frequencies --- -1.4878 -0.0015 -0.0002 0.0096 0.6540 0.6540 Low frequencies --- 76.3920 76.3924 99.6767

Wavenumber/cm-1	Intensity	IR active?	Type
76	3	Yes (Weak)	Bend
76	3	Yes (Weak)	Bend
100	9	Yes (Weak)	Bend
197	0	No	Stretch (Symmetric)
316	57	Yes	Stretch (Asymmetric)
316	57	Yes	Stretch (Asymmetric)

Questions

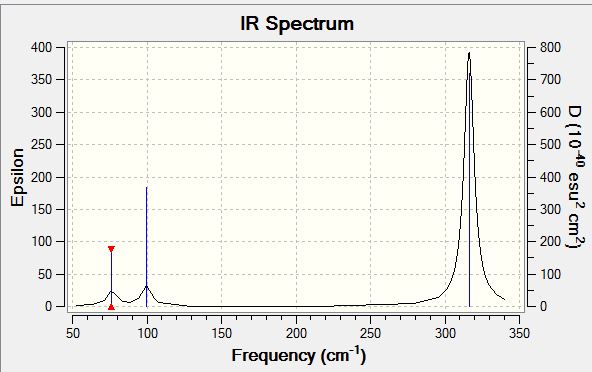
Both BH₃ and GaBr₃ have 6 different vibrational modes, as they are both non-linear and have 4 atoms in the system. Both molecules have 5 IR active modes with 2 degenerate pairs (as they both have the same trigonal planar structure). The most obvious difference is the large gap in IR frequencies, with all of the GaBr₃ being below 320 cm^-1, and the lowest in BH₃ being over 1160 cm^-1. This can be rationalised by the difference in size and bond strength of the two molecules, whereby GaBr₃ is much larger and possesses weaker bonds, which vibrate at a much lower frequency, and are also less intense than their BH₃ counterparts. The force constant, k, for GaBr₃ has decreased and the reduced mass has increased, which according to the simple harmonic motion formula where vibrational frequency is proportional to the square root of k/reduced mass, and therefore is at lower frequency, thus indicating the much weaker Ga-Br bonds.²

There is also a change in order of the modes, with the A2" umbrella motion moving from lowest frequency in BH₃ to the third lowest in GaBr₃, rationalised by the change in masses of the atoms, where boron is heavier than hydrogen (heavier than the combination of 3 also in fact), whereas gallium is lighter than bromine. In the animation for BH₃, the hydrogen atoms perform the majority of the vibrational movement, whereas in GaBr₃, the converse is true with the central gallium moving a greater displacement than the outer bromines. This is a greater overall frequency of movement, relative to other vibrations and hence is higher up in the vibrational series.

In order for a valid analysis to be conducted, the same method and basis set must be used otherwise large energy differences may be observed due to the difference in accuracy level of the varying calculations. If this were the case, a valid comparison could not be made. A frequency analysis is conducted in order to assess whether optimisation has been completed successfully or not and to ensure the compound calculated on is not a transition state and is indeed the minimum in energy. If the frequency analysis comes back with negative frequencies, then it has been calculated on a transition state instead. The "low frequencies" represent the minute variations from the optimised structure when performing the frequency analysis and are caused by translations and rotations about the centre of mass, in addition to the vibrational modes.

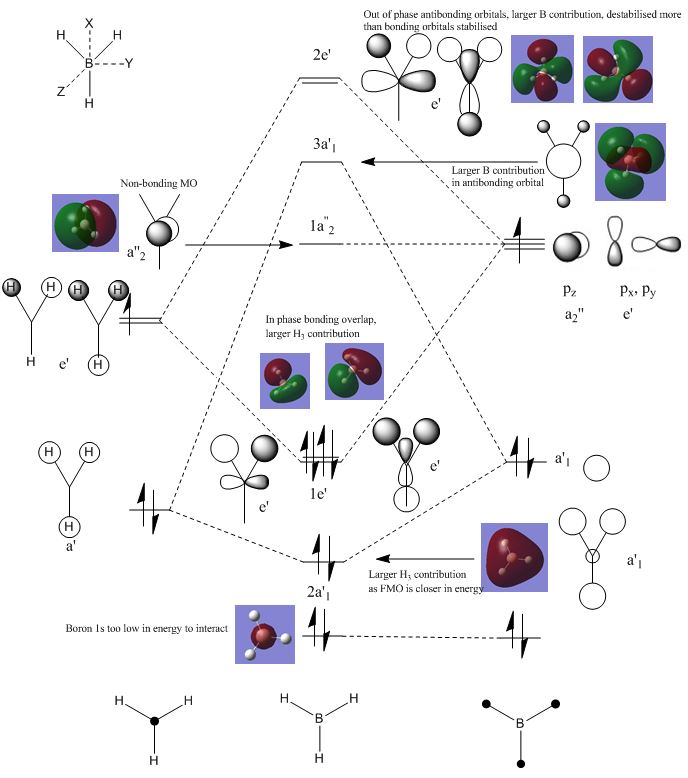
BH₃ Molecular Orbital Analysis B3LYP/6-31G

DOI:10042/143673

Questions

As can be seen from the orbital diagrams above, the real and LCAO MO's show a very good comparison, with the s-character orbitals in particular showing a very similar shape for both real and LCAO MO's. At higher energies, such as those for the unoccupied orbitals, the LCAO theory starts to break down, but for all relevant orbitals, up to the LUMO +2, the approximation is quite accurate. As there is good overlap between the similarly electronegative boron and hydrogen, the orbitals are all recognisable shapes, and are not significantly polarised. It can be seen that the optimisation was not completely successful though, with slightly skewed orbitals in some cases, which should, in theory, be completely symmetrical.

NH₃ B3LYP/6.21G(d,p)

Optimisation log file here

Summary Data	Convergence	Jmol
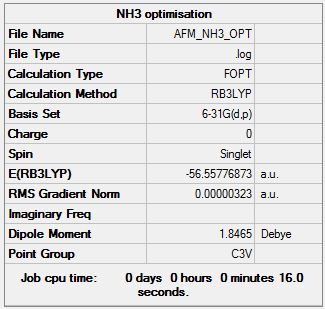	Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000012 0.001800 YES RMS Displacement 0.000008 0.001200 YES Predicted change in Energy=-9.843882D-11 Optimization completed.	Optimised NH3

Frequency Analysis B3LYP/6.21G(d,p)

Frequency log file here

Summary Data	Low modes
	Low frequencies --- -0.0128 -0.0012 0.0018 7.0724 8.1020 8.1023 Low frequencies --- 1089.3849 1693.9369 1693.9369

Wavenumber/cm-1	Intensity	IR active?	Type
1089	145	Yes	Bend
1694	14	Yes (Weak)	Bend
1694	14	Yes (Weak)	Bend
3461	1	No	Stretch (Symmetric)
3590	0	No	Stretch (Asymmetric)
3590	0	No	Stretch (Asymmetric)

Population Analysis B3LYP/6.21G(d,p)

Population analysis: DOI:10042/143685

Atom	Charge
H	0.375
N	-1.125

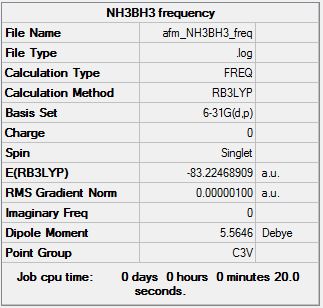
Optimization of BH₃NH₃

Optimisation log file here

Summary Data	Convergence	Jmol
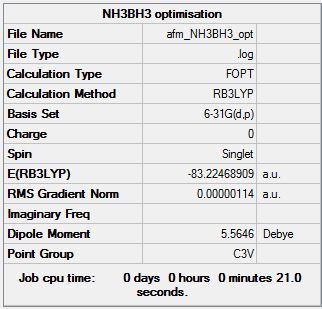	Item Value Threshold Converged? Maximum Force 0.000002 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000009 0.000060 YES RMS Displacement 0.000002 0.000040 YES Predicted change in Energy=-2.750138D-11 Optimization completed.	Optimised NH3BH3

Frequency analysis B3LYP/6.21G(d,p)

Frequency log file here

Summary Data	Low modes
	Low frequencies --- -5.1672 -0.3088 -0.0453 0.0010 1.1923 1.2688 Low frequencies --- 263.2988 632.9555 638.4580

Wavenumber/cm-1	Intensity	IR active?	Type
263	0	No	Bend
633	14	Yes (Weak)	Stretch
638	4	No	Bend
638	4	No	Bend
1069	41	Yes	Bend
1069	41	Yes	Bend
1196	109	Yes	Bend
1204	3	No	Bend
1204	3	No	Bend
1329	114	Yes	Bend
1676	28	Yes	Bend
1676	28	Yes	Bend
2472	67	Yes	Stretch
2532	231	Yes	Stretch
2532	231	Yes	Stretch
3464	3	No	Stretch
3581	28	Yes	Stretch
3581	28	Yes	Stretch

E(NH3) = -56.55776873 au

E(BH3) = -26.61532350 au

E(NH3BH3) = -83.22468909 au

ΔE = E(NH3BH3) - [E(NH3) + E(BH3)]

ΔE = (-83.22468909) - (-83.17309223)

ΔE = -0.05159686 au = -135.47 kJ/mol

Using the discussion made previously, this can be described as a weak bond, similar in energy to the iodine-iodine single bond mentioned above. It isn't as weak as most hydrogen bonds, (although it can be argued that these are not strictly "bonds" in the same sense) but is as weak as some of the weakest covalent interactions. It is of appropriate magnitude, and is not an excessively large or small so can be deemed a sensibly accurate result.

Introduction

Not all bonds are as straight forward as a mutually beneficial sharing of two electrons between 2 atoms, 2c-2e (2-centre, 2-electrons) bonds. In systems such as B₂H₆, electron density is shared between three atoms at a time, with hydrogens "bridging" between both boron atoms. These 3c-2e bonds are different to the exhibited 2c-2e terminal B-H bonds, with the bridging B-H bonds having a bond length of 133 pm whereas the terminal B-H bonds have a length of 119 pm. The relative strengths of these bonds can be shown by their IR spectra, where bridging B-H bonds show a vibration at ~2100 cm^-1 and terminal at ~2500 cm^-1, where typically a higher vibrational wavenumber indicates a stronger bond.³

The initial suggested structure to explain this behaviour, with a D_2H point group as proposed by Longuet-Higgins, is shown below.⁴

Figure 1: Proposed structure of diborane, with tetrahedral boron atoms and bridging hydrogens.

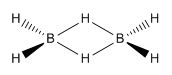
Longeut-Higgins could not however explain why there was still a boron-boron vibration present, which can now be explained through the interactions of its molecular orbitals.

In a similar manner, it is suggested that Al₂Cl₄Br₂ also adopts a dimeric structure with bridging chlorine or bromine atoms. In order to assess which is the most stable dimeric conformation, and if indeed a dimeric structure is more favourable that monomeric, a series of calculations was carried out, using the following isomers:

Figure 2: 6 different isomers of Al₂Cl₄Br₂, including enantiomers.

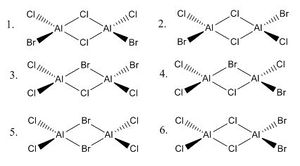
As can be seen above, isomers 1 and 2 are cis/trans bromine variants of one another, and isomers 3 and 4 are mirror-image enantiomers of each other. When first observing isomer 6, one might suggest that it has not been produced by 2 distinct AlCl₂Br monomers, but as will be discussed later, through a dynamic equilibrium, this conformation is also possible.

Isomeric Optimisation

Note, all optimisations below were performed after imposing the point group symmetry onto each molecule, as Gaussian cannot always accurately determine this during its calculations. Optimisations were performed using the same criteria as before, with the same checks made to assure the steps were not completed on a transition state.

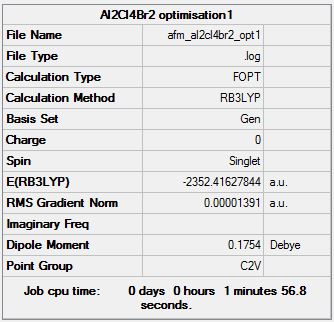
Isomer 1

Optimisation log file here

DOI:10042/150003

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000016 0.000450 YES RMS Force 0.000009 0.000300 YES Maximum Displacement 0.000861 0.001800 YES RMS Displacement 0.000245 0.001200 YES Predicted change in Energy=-5.654014D-10 Optimization completed.	Optimised Al2Cl4Br2

Frequency Analysis

Frequency log file here

DOI:10042/150005

Summary Data	Low modes
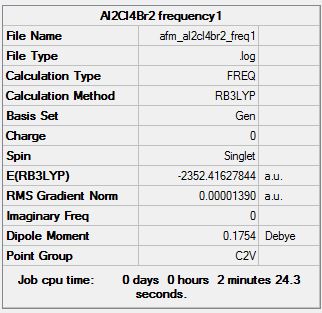	Low frequencies --- -1.3642 -0.7174 0.0009 0.0017 0.0023 2.2122 Low frequencies --- 17.4868 51.1472 78.5167

Wavenumber/cm-1	Intensity	IR active?	Type
17	0	No	Bend
51	0	No	Bend
79	0	No	Bend
99	0	No	Bend
103	3	No	Bend
121	13	Yes (Weak)	Bend
123	6	Yes (Weak)	Bend
157	0	No	Bend
158	5	Yes (Weak)	Bend
194	2	No	Stretch
263	0	No	Stretch
279	26	Yes	Stretch
308	2	No	Stretch
413	149	Yes	Stretch
419	410	Yes	Stretch
461	35	Yes	Stretch
571	33	Yes	Stretch
583	277	Yes	Stretch

Isomer 2

Optimisation log file here

DOI:10042/150007

Summary Data	Convergence	Jmol
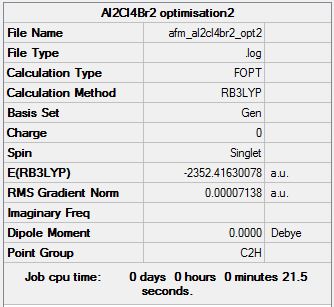	Item Value Threshold Converged? Maximum Force 0.000163 0.000450 YES RMS Force 0.000043 0.000300 YES Maximum Displacement 0.000542 0.001800 YES RMS Displacement 0.000194 0.001200 YES Predicted change in Energy=-1.483080D-07 Optimization completed.	Optimised Al2Cl4Br2

Frequency Analysis

Frequency log file here

DOI:10042/150010

Summary Data	Low modes
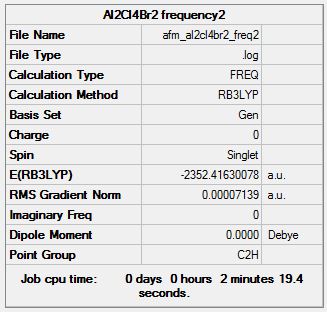	Low frequencies --- -0.6157 -0.0053 -0.0043 -0.0043 1.9696 4.0000 Low frequencies --- 18.6070 49.3252 72.9226

Wavenumber/cm-1	Intensity	IR active?	Type
19	0	No	Bend
49	0	No	Bend
73	0	No	Bend
105	0	No	Bend
109	3	No	Bend
118	9	Yes (Weak)	Bend
120	13	Yes (Weak)	Bend
157	0	No	Bend
159	6	Yes (Weak)	Bend
192	0	No	Stretch
264	0	No	Stretch
280	29	Yes	Stretch
308	0	No	Stretch
413	149	Yes	Stretch
421	438	Yes	Stretch
459	0	No	Stretch
574	0	No	Stretch
579	316	Yes	Stretch

Isomer 3

Optimisation log file here

DOI:10042/150028

Summary Data	Convergence	Jmol
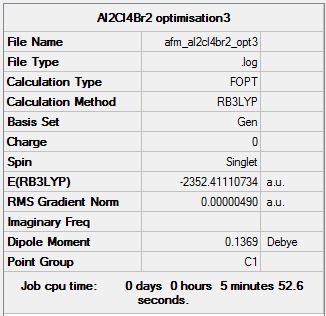	Item Value Threshold Converged? Maximum Force 0.000010 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000421 0.001800 YES RMS Displacement 0.000156 0.001200 YES Predicted change in Energy=-1.781167D-09 Optimization completed.	Optimised Al2Cl4Br2

Frequency Analysis

Frequency log file here

DOI:10042/150034

Summary Data	Low modes
	Low frequencies --- -0.5522 -0.0024 -0.0018 -0.0018 0.8963 1.6897 Low frequencies --- 16.9322 55.9187 80.0655

Wavenumber/cm-1	Intensity	IR active?	Type
17	0	No	Bend
56	0	No	Bend
80	0	No	Bend
92	0	No	Bend
107	3	No	Bend
110	5	Yes (Weak)	Bend
121	8	Yes (Weak)	Bend
149	5	Yes (Weak)	Bend
155	6	Yes (Weak)	Bend
186	1	No	Stretch
211	21	Yes	Stretch
257	10	Yes (Weak)	Stretch
289	48	Yes	Stretch
384	153	Yes	Stretch
424	275	Yes	Stretch
493	107	Yes	Stretch
575	122	Yes	Stretch
615	197	Yes	Stretch

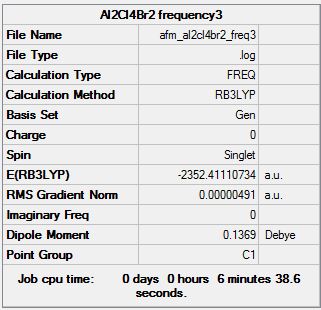
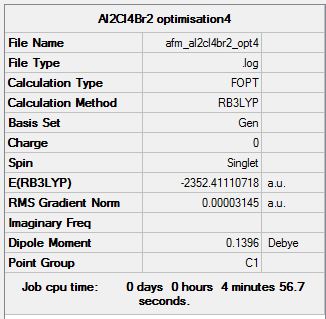
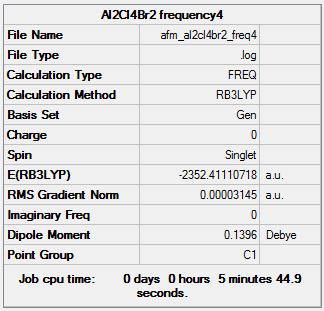
Isomer 4

Optimisation log file here

DOI:10042/157844

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000074 0.000450 YES RMS Force 0.000030 0.000300 YES Maximum Displacement 0.000968 0.001800 YES RMS Displacement 0.000403 0.001200 YES Predicted change in Energy=-8.186031D-08 Optimization completed.	Optimised Al2Cl4Br2

Frequency Analysis

Frequency log file here

DOI:10042/157850

Summary Data	Low modes
	Low frequencies --- -1.0720 -0.0034 -0.0026 0.0011 1.3940 1.9188 Low frequencies --- 16.9537 55.8869 80.0642

Wavenumber/cm-1	Intensity	IR active?	Type
17	0	No	Bend
56	0	No	Bend
80	0	No	Bend
92	1	No	Bend
107	3	No	Bend
110	5	Yes (Weak)	Bend
121	8	Yes (Weak)	Bend
149	5	Yes (Weak)	Bend
154	6	Yes (Weak)	Bend
186	1	No	Stretch
211	21	Yes	Stretch
257	10	Yes (Weak)	Stretch
289	48	Yes	Stretch
384	153	Yes	Stretch
424	275	Yes	Stretch
493	107	Yes	Stretch
575	122	Yes	Stretch
615	197	Yes	Stretch

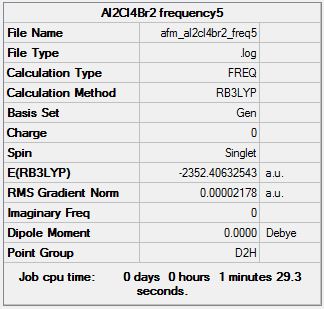
Isomer 5

Optimisation log file here

DOI:10042/157889

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000042 0.000450 YES RMS Force 0.000018 0.000300 YES Maximum Displacement 0.000924 0.001800 YES RMS Displacement 0.000298 0.001200 YES Predicted change in Energy=-1.919413D-10 Optimization completed.	Optimised Al2Cl4Br2

Frequency Analysis

Frequency log file here

DOI:10042/157898

Summary Data	Low modes
	Low frequencies --- -0.4550 -0.0039 -0.0025 -0.0024 1.3606 1.6872 Low frequencies --- 16.0957 63.6185 86.1024

Wavenumber/cm-1	Intensity	IR active?	Type
16	0	No	Bend
64	0	No	Bend
86	0	No	Bend
87	0	No	Bend
108	5	Yes (Weak)	Bend
111	0	No	Bend
126	8	Yes (Weak)	Bend
135	0	No	Bend
138	7	Yes (Weak)	Bend
163	0	No	Stretch
197	0	No	Stretch
241	100	Yes	Stretch
247	0	No	Stretch
341	161	Yes	Stretch
468	346	Yes	Stretch
494	0	No	Stretch
609	0	No	Stretch
617	332	Yes	Stretch

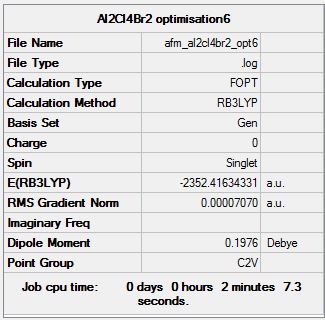
Isomer 6

Optimisation log file here

DOI:10042/157918

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000171 0.000450 YES RMS Force 0.000047 0.000300 YES Maximum Displacement 0.001362 0.001800 YES RMS Displacement 0.000405 0.001200 YES Predicted change in Energy=-3.621078D-07 Optimization completed.	Optimised Al2Cl4Br2

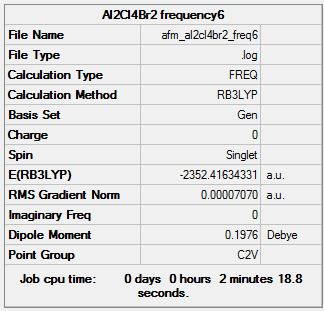
Frequency Analysis

Frequency log file here

DOI:10042/157922

Summary Data	Low modes
	Low frequencies --- -0.0007 0.0020 0.0047 1.4161 2.6788 3.6283 Low frequencies --- 18.8512 51.2590 72.1839

Wavenumber/cm-1	Intensity	IR active?	Type
19	0	No	Bend
51	0	No	Bend
72	1	No	Bend
98	0	No	Bend
112	0	No	Bend
112	8	Yes (Weak)	Bend
120	11	Yes (Weak)	Bend
160	1	No	Bend
166	7	Yes (Weak)	Bend
187	2	No	Stretch
263	0	No	Stretch
270	14	Yes (Weak)	Stretch
322	41	Yes	Stretch
413	150	Yes	Stretch
418	308	Yes	Stretch
495	134	Yes	Stretch
503	105	Yes	Stretch
616	177	Yes	Stretch

Discussion

As can be seen from the tables above, the lowest energy isomer is isomer 6, with both bromine atoms on the same aluminium atom, and thus the energies relative to the lowest energy conformer are with reference to this isomer.

Isomer 1: 0.170 kJ/mol

Isomer 2: 0.112 kJ/mol

Isomer 3: 13.7 kJ/mol

Isomer 4: 13.7 kJ/mol

Isomer 5: 26.3 kJ/mol

Isomer 6: 0 kJ/mol

As can be seen from these data, the highest energy conformation is isomer 5, with both bromines bridging between aluminiums. It would be quick and easy to place an order on these based on the numbers above, however, this is not strictly accurate, as the calculations have an error of ±10 kJ/mol, and hence from this error it cannot be concluded that isomers 1, 2 and 6 are in fact of different energies. We can only assume degeneracy is the case. Isomer 3 and 4 both show the same energies relative to isomer 6, which is the expected result as they are both enantiomers of each other, with no chemical difference.

It can be seen that the most stable conformations all have bromine atoms terminal and not bridging. This can be rationalised due to chlorines superior ability to donate electron density to the electron deficient aluminium atoms, when bridging. If we base our stability argument purely on the halogens ability to act as sigma donors into empty p-orbitals, theorising a purely dative covalent bond from the bridging halogens, then one would expect isomer 5 with bromines bridging to be most stable, as bromine is happier to donate its lone pair than chlorine is. This is clearly not the case however and as such, other factors must be considered. As you go down group 3, the tendency to oligomerise increases. Boron typically forms monomers whereas aluminium tends to dimerise. They are each electron deficient and possess an orthogonal empty p-orbital into which pi donation can occur. The overlap of this p-orbital with a filled p-orbital on bonded atoms, in this case, halogens, directly affects the stabilisation that the central atom achieves. Due to size constraints, this overlap is most beneficial to boron and is hence stabilised greatest. For aluminium however, the overlap is with one of aluminiums 3p orbitals, as opposed to borons 2p orbital, and hence is less significant as the orbitals are more diffuse. Therefore aluminium must look for additional ways to stabilise itself as the pi donation is only weak, and thus a dimeric structure with addition electron donation is favoured. Combining this with the electron donation argument, it is clear that orbital overlap is key in determining stabilisation factors. Aluminium and chlorine are both in the 3rd row of the periodic table and are fairly similar in orbital size. Bromine is in row 4 however and possesses a large amount of extra electrons in comparison to chlorine. Since chlorine will donate from the same sub level as aluminiums acceptor orbitals, it is expected that good overlap is achieved, in contrast to donation from a bromine 4p orbital, which is more diffuse in the first place, and hence will not achieve as successful of an overlap. This leads to the assessment that the isomers without bridging bromines should be most stable, which is in agreement with the energy data presented above. This argument ignores any others interactions, such as those present between aluminium atoms and assumes that these are similar for each isomer and so don't affect the stability argument. These would have to be considered if different metals were being analysed in turn, as it would be expected that different nuclei have differing affects on stability. Further studies comparing the lowest energy isomer above, and a similar one with gallium instead of aluminium could be conducted to try and assess this affect. This would not be trivial though, as stated before, as we move down the group, the tendency to oligomerise and subsequently polymerise increases, so finding a directly comparable dimerically structured molecule may be difficult. Interestingly, it can be seen from the energy data above that adding a bromine molecule bridging increases the energy by about 13 kJ/mol at a time. Interesting to examine are the vapour pressures when Al₂Cl₆ and Al₂Br₆ are mixed at room temperature to produce Al₂Cl₄Br₂, as discussed by Dunne and Gregory.⁵

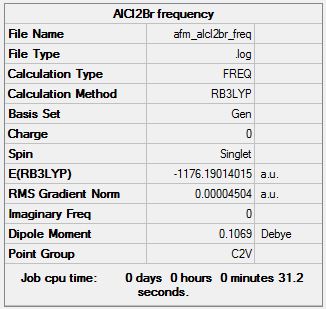
The monomer AlCl₂Br, as shown below, is what forms each of the dimers above. Via a dynamic equilibrium of ligand exchange, both bromines can be transferred onto one aluminium atom, which is what gives the lowest energy conformation.

AlCl₂Br Monomer

Optimisation log file here

DOI:10042/160767

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000149 0.000450 YES RMS Force 0.000078 0.000300 YES Maximum Displacement 0.000797 0.001800 YES RMS Displacement 0.000541 0.001200 YES Predicted change in Energy=-9.241428D-08 Optimization completed.	Optimised AlCl2Br

Frequency Analysis

Frequency log file here

DOI:10042/160770

Summary Data	Low modes
	Low frequencies --- -0.0036 -0.0035 -0.0022 3.3756 3.6552 4.1209 Low frequencies --- 120.7185 133.9343 185.8750

From these data the relative stability of the dimer over monomeric structure can be calculated as such:

ΔE = E(Al2Cl4Br2) - [E(AlCl2Br) + E(AlCl2Br)]

= 6176174.896404 kJ/mol - 6176269.5798437 kJ/mol

ΔE = -0.03606 au = -94.68 kJ/mol

So as can be seen, the most stable dimer is almost 100 kJ/mol more stable than the two separate monomers, as is expected from the pi stabilisation effect.

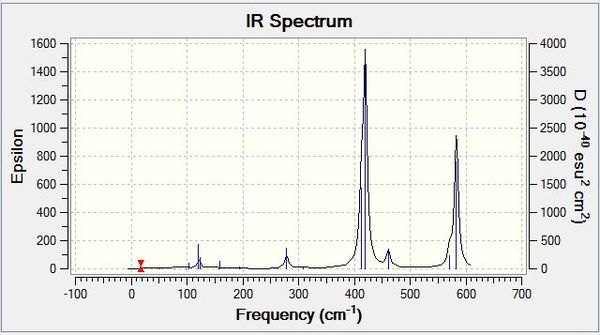
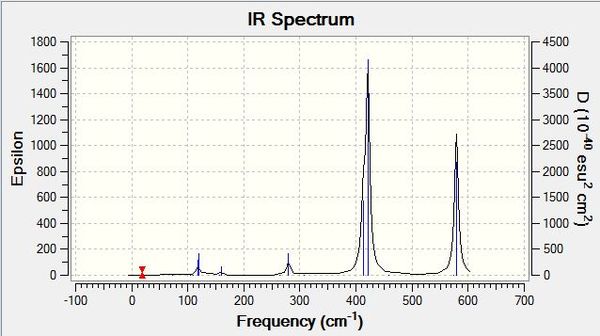
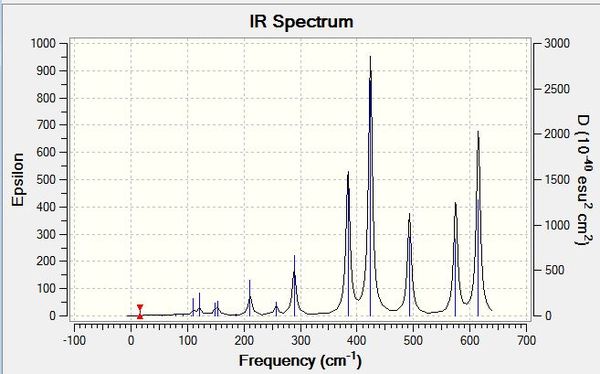
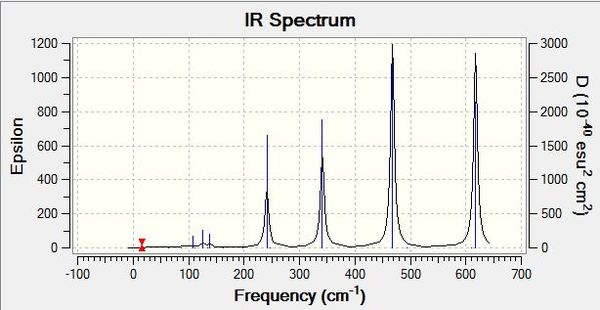
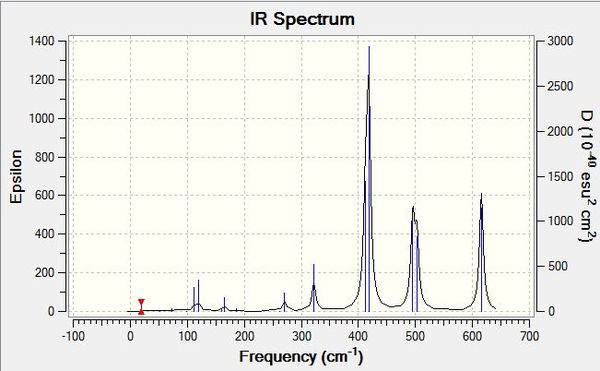
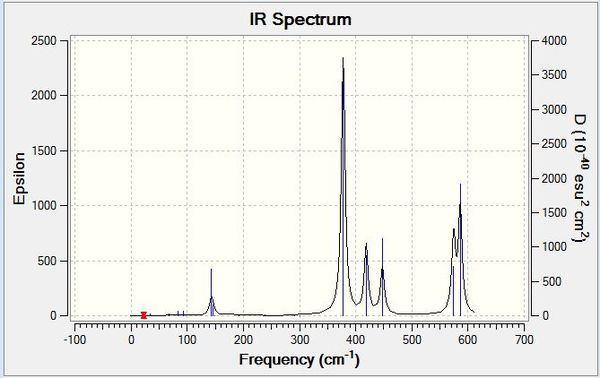
Each of the IR spectra of the isomers shows only the active bands. For a band to be IR active there must be a change in overall dipole moment, which is not always the case for certain vibrations. For simplicity, extremely weakly active bands are marked as non-IR active. The quantity of active bands is determined by the molecules symmetry and since each of the isomers has a different point group, they have different amounts of IR active bands. The lower the symmetry of a molecule, the greater the number of IR active bands. If a molecule is less symmetrical, more of its bond stretches will be asymmetric as opposed to symmetric, which results in a change in dipole moment. It stands to reason then that the least symmetrical molecule, isomers 3 and 4 with point group C₁, will have the most IR active bands, which is evidently the case, showing seven intensely active bands with an intensity greater than 15 (arbitrarily chosen). This is in stark contrast to the most symmetrical molecule, isomer 5, with point group of D_2H, which has just four intensely IR active bands. Various weak signals are seen in most of the isomers, as even though there are different atoms attached to the aluminiums, bromine and chlorine are quite similar, so some seemingly symmetrical movements show a change in dipole due to the albeit small difference between the atoms in question. As is also expected, intermediately symmetrical molecules, such as isomers 1 and 6 with point group C_2V and isomer 2 with point group C_2H, show an intermediate amount of IR active bands. 1 and 6 both show the same amount of bands, six, in agreement with our point group argument, and the more symmetrical isomer 2 shows four bands like isomer 5.

When we change the position of the bromine atoms, between bridging and terminal, we see observable differences in the nature of the Al-Br stretches. Tabulated below are the terminal Al-Br stretches and the bridging Al-Br stretches.

Molecule	Wavenumber/cm-1	Intensity
Isomer 1	420 & 461	410 & 35
Isomer 2	421 & 459	438 & 0
Isomer 3	424	275
Isomer 4	424	275
Isomer 5	-	-
Isomer 6	495	134

Table 1: Terminal Al-Br stretches

Molecule	Wavenumber/cm-1	Intensity
Isomer 1	263 & 279	0 & 26
Isomer 2	264 & 280	0 & 29
Isomer 3	211 & 257	21 & 10
Isomer 4	211 & 257	21 & 10
Isomer 5	241 & 247	100 & 0
Isomer 6	-	-

Table 2: Bridging Al-Br stretches

Note: For isomers 1, 2, and 6, bridging "Al-Br" bonds are not present so some appropriate data for bridging "Al-Cl" bonds is provided for comparison instead.

For some vibrations, the stretch seen is mainly between aluminium and chlorine, which is as expected due to the mass mismatch between chlorine and bromine. As such, the data reported above is such as to focus on what appear to be mainly Al-Br stretches.

Both symmetric and asymmetric stretches have been reported for most of the isomers above, even though some of the "symmetric" stretches are not IR active, they still show an interesting comparison. Focusing first on terminal Al-Br stretches, it is seen that isomer 6 with two terminal bromines vibrates at the highest frequency wavenumber but at the lowest intensity. Al-Br bonds are weaker than their Al-Cl counterparts, as discussed previously, and hence do not vibrate as vigorously. This trend continues when bromines are replaced with chlorines, so when there is one of each atom present on aluminium, the vibration is intermediate of when there are two chlorines or two bromines on the aluminium. This is in line with the bond strengths and orbital overlap arguments. It is also noted that the terminal stretches are all much higher frequencies than the bridging stretches, another expected consequence, but this time of the difference in covalent bonding type between the atoms. The terminal stretches are 2c-2e bonds whereas the bridging stretches are 3c-2e bonds and thus much weaker. The stronger a bond, the higher frequency it vibrates at. With regards to the bridging stretches, isomers 1 and 2 with just bridging chlorines showed the highest frequency of vibration. Interestingly, while it was at a higher frequency, it was not significantly higher than those of bromine. The small amplitude of the bond length variations is a reason these values are quite similar, with the stretching not occurring over a significant distance. Of the bridging bromine isomers, when two bromines were present bridging, the vibration was at its highest frequency and most intense (for the active asymmetric mode). When observing the stretches, the much heavier bromines appear to fix the molecule in place at times, and conversely when bromines are vibrating simultaneously, the rest of the molecule vibrates around them with a large amplitude. Thus the arguments to explain the bridging trends appear in converse to the arguments for terminal stretches, with the weaker Al-Br bonds in fact sometimes producing a more intense vibration than the Al-Cl analogue, and the symmetry of having two bridging bromines perhaps as centrally massive atoms, leading to more intense vibrations across the rest of the molecule.

Examples of some of the stretches in question are shown below:

Figure 3: Isomer 1, terminal stretch.

Figure 4: Isomer 4, bridging stretch.

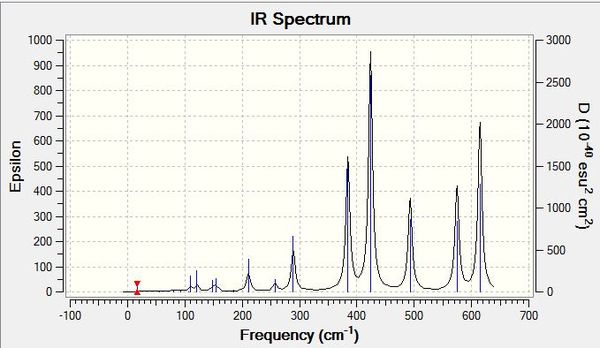
Also briefly studied was the theoretical trimer Al₃Cl₆Br₃, with the isomers chosen having bridging chlorine atoms and cis terminal bromine atoms on the aluminiums for one and two bromines on one aluminium for the other, in order to see if the molecule can be optimised to a stable minimum and which of these two structures would be of the lowest energy. Results of the optimisations are shown below:

Al₃Cl₆Br₃ (cis bromines)

Optimisation log file here

DOI:10042/161053

Summary Data	Convergence	Jmol
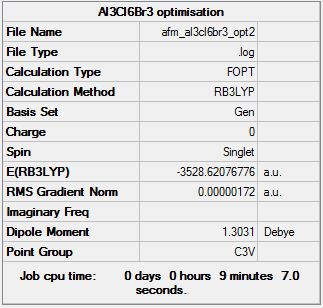	Item Value Threshold Converged? Maximum Force 0.000002 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000071 0.001800 YES RMS Displacement 0.000025 0.001200 YES Predicted change in Energy=-1.736612D-10 Optimization completed.	Optimised Al3Cl6Br3

Frequency Analysis

Frequency log file here

DOI:10042/161054

Summary Data	Low modes
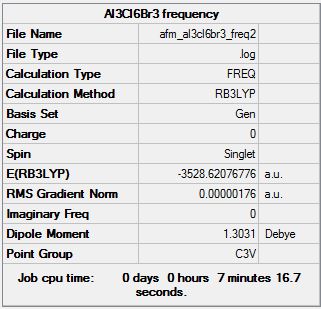	Low frequencies --- -2.3702 -2.3659 -2.2217 0.0051 0.0075 0.0143 Low frequencies --- 23.2884 23.2889 34.6103

As can be seen, a successful optimisation of this molecule was achieved. The terminal Al-Br stretches were seen at 448 cm^-1 and two degenerate modes at 419 cm^-1. These frequencies are interestingly fairly similar to the dimer structures above, but are of lower intensities of 125 and 91 respectively. The large bromines appear to have an even greater anchoring effect in the trimer than in the dimer, therefore reducing the amplitude of their vibrations. This molecule is highly symmetric with a C_3V point group and hence has only 10 strongly IR active modes, despite its much increased modes of freedom over the dimer. An image of the IR frequencies table is shown below:

Table 3: Al₃Cl₆Br₃ vibrations.

Unfortunately, all attempts to optimise the alternative theorised structure were unsuccessful and hence no data is presented. The above optimised structure is likely stabilised by an additional pi interaction of the cis bromine p-orbitals, which the alternative does not possess.

Molecular Orbital Analysis

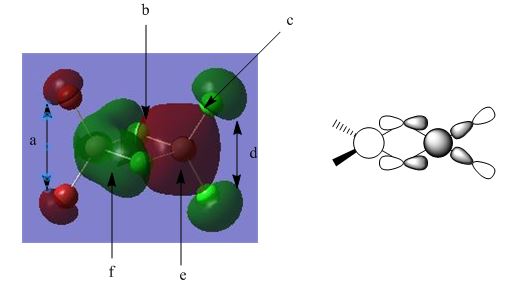
The occupied molecular orbitals (MO's) of the most stable conformation, isomer 6, were visualised in Gaussian via the formatted checkpoint file. Presented below are a range of non-core MO's, from bonding to antibonding combinations. Also presented are the suggested linear combination of atomic orbitals (LCAO's), responsible for the MO's. The initial calculations can be found in the frequency file of isomer 6 presented previously.

Molecular Orbital 37

This is the lowest energy non-core orbital and is overall bonding in its character,

Figure 5: MO 37 with LCAO.

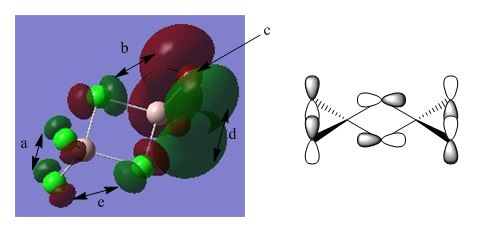
A: A weakly bonding, in phase interaction between p-orbitals on terminal bromines. These orbitals do not contribute largely to the central orbitals and hence are left out of the LCAO drawing.

B: Nodal planes runs through the centre of the bridging chlorine atoms. The uneven nature of the MO here is of interest as it shows how the difference in electronegativities of the terminal atoms, with chlorine being more electronegative than bromine, skewing the orbital shape, with a greater electron density being attracted to the more electronegative terminal chlorines. Present in the centre of the two aluminium atoms is an antibonding, out of phase interaction, and causes the uneven distribution of the large central MO's, with the one presented in green appearing to "bend" away from the centre.

C: Nodal Plane between large red shaded orbital and opposite phase of chlorine p-orbital.

D: Similar to interaction A above, a weakly bonding, in phase interaction between p-orbitals on terminal chlorines.

E: Large orbital showing no nodes, with a large contribution from central aluminium 3s orbital (hence the rather spherical shape). Electron density is distributed quite evenly across the contributing atoms, both bridging chlorines, aluminium and both terminal bromines. Nodal planes can be seen passing through chlorine atoms. The strong bonding interaction seen here between aluminium 3s and chlorine p-orbitals is also evident throughout the molecule, contributed to the good overlap between the atoms 3rd sub level orbitals. In contrast to bromines p-orbitals, where the overlap and direct interaction is weaker with aluminiums 3s due to the size mismatch.

F: Similar to point E above, but now more polarised towards aluminium, due to the increased size of terminal atoms, where bromine is more less electronegative than chlorine and hence does not hold electron density quite as closely.

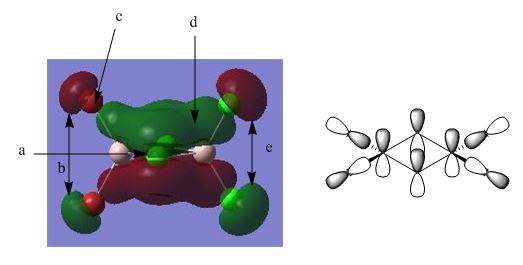
Molecular Orbital 40

Figure 6: MO 40 with LCAO.

A: This point shows the nodal plane passing through the central four atom cores, between the pi-bonding bridging interactions described below.

B: Weakly antibonding, through space interaction between terminal bromines.

C: Node at the centre of interacting p-orbital of terminal bromines.

D: This MO is dominated by this strongly bonding pi interaction between the central aluminiums and bridging chlorines p-orbitals. This describes the 3c-2e electron bonding situation quite nicely in diagram form.

E: Similar to B above, a through space, weakly antibonding interaction between terminal chlorines. An additional weakly bonding interaction, between terminal chlorines on one side and terminal bromines on the other side, are present, although the lack of proximity of these orbitals means this contribution is small at best.

This MO is also overall bonding in character and is clear portrayal of the pi-interactions between central p-orbitals.

Molecular Orbital 44

Figure 7: MO 44 with LCAO.

A: Weakly antibonding through space interaction of terminal chlorine p-orbitals.

B: Same as above.

C: Bonding through space interaction between terminal chlorine p-orbitals and bridging chlorine p-orbitals. Close proximity due to large central orbital size means this interaction is greater than the weakly antibonding interactions above. It cannot be described as strong though, as typical that label would be reserved for directly overlapping interactions.

D: Same as C, both phases of terminal chlorine p-orbitals interact in phase with the orthogonal bridging chlorine p-orbitals.

E: Antibonding through space interaction. Fairly significant interaction due to largely dominant, close proximity, bridging chlorine p-orbitals in this MO.

F: Large nodal plane running through central aluminum and chlorine atoms, through the centre of the bridging chlorine p-orbitals.

This orbital would be slightly antibonding in nature, with the direct proximity and large contribution of central bridging chlorine orbitals winning over the diagonal interaction from less significant terminal chlorine p-orbitals. The central orbitals have a lsight elongation at each end which also suggests that a through bond interaction with the bridging chlorines and aluminiums is present, but is not shown in this case.

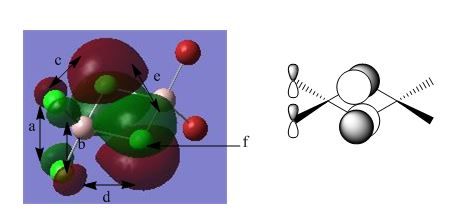
Molecular Orbital 48

Figure 8: MO 48 with LCAO.

A: Weak through space bonding interaction between terminal bromine p-orbitals. Only small contributions from these orbitals are present.

B: Weak through space bonding interaction between terminal bromine p-orbital and bridging chlorine p-orbital

C: Moderate antibonding through space interaction between very large terminal chlorine p-orbitals and smaller contributing bridging chlorine p-orbital. A possible weakly bonding interaction between the terminal chlorines p-orbital and the other phase of the bridging chlorines p-orbital may be present, but would be insignificant in comparison, so can be largely ignored.

D: Strong pi-bonding interaction between neighbouring terminal chlorine p-orbitals. A nodal plane is seen through the centres of these orbitals. Interestingly, as seen below, this interaction is seemingly almost identical in size and contribution to the pi-bonding between bromine p-orbitals in MO 52.

Interactions between bridging chlorine p-orbitals will also contribute and will be antibonding in nature, with a moderate strength due to being through space and not directly through a atoms and a bond.

This orbital is bonding in character, with the largest contributions being from bonding interactions. The p-orbitals on the terminal chlorines dominate in this case, as shown by the LCAO diagram above.

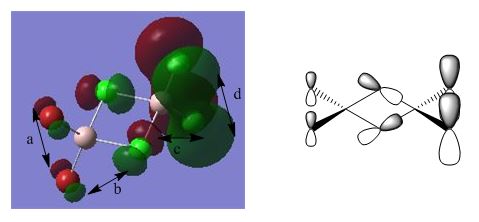
Molecular Orbital 52

Figure 9: MO 52 with LCAO.

Similar to orbital 48 above, but now with the dominating orbitals coming from the terminal bromines as opposed to the terminal chlorines and slightly different orientation of bridging chlorine p-orbitals.

A: As before, a weakly bonding through space interaction, but now between terminal chlorine p-orbitals as opposed to bromines.

B: As point C above, antibonding in nature. Directionality is slightly different due to now orthogonal orientation of bridging chlorine p-orbitals. This would slightly increase the strength of this interaction, but not to a significant degree.

C: Distinct nodal plane, as seen through the centre of all p-orbitals, is seen here between pi-bonding interaction of bromine orbitals.

D: As point D above, a strong bonding pi interaction between neighbouring terminal bromines p-orbitals. Largest contribution to the MO comes from this interaction. Symmetry of the molecule leaves these orbitals in a nice circular arrangement, with no skewed polarisation.

E: As point B of MO 48, but now antibonding as opposed to bonding.

Slightly weaker than in MO 48 will be the interactions between bridging chlorines, as the new directionality separates them slightly more than before. As through space interaction are based on the vicinity of the orbitals to one another, this greater distance reduces the strength of this antibonding interaction by a small amount.

Overall this orbital would likely be antibonding, due to the greatest contributing factors being from the pi interactions of the bromine p-orbitals, where despite this appears bonding, bromines have a larger coefficient than chlorine and will be higher up in an MO diagram, and hence contribute more to the overall antibonding character of the molecule. The generality is what must be focussed on as opposed to the direct portion of the molecule.

Conclusion

This project, focusing on the Lewis acidity and basicity of the dimer Al₂Cl₄Br₂, has demonstrated how the distribution of bromine atoms across the molecule affects the stability and vibrational activity. The lowest energy conformation was found and molecular orbital analysis was conducted on five of its non-core orbitals. Isomer 6 with two bromine atoms terminal on one aluminium, generated by a dynamic exchange equilibrium, was found to be most stable, but within the error range of the calculations, this could not be ascertained for definite.

Further experiments could involve the change of central metal atom, to gallium for example, or change of some of the halogen components, introducing an iodine atom into the system for example. It would be expected that the most stable isomers would have the lowest mass halogens in the system bridging, for the same reasons as chlorine bridging is more stable than bromine bridging.

References

1. B. Cordero, V. Gómez, A. E. Platero-Prats, M. Revés, J. Echeverría, E. Cremades, F. Barragán and S. Alvarez, Dalt. Trans., 2008, 21, 2832–2838.

2. P. Gans, Vibrating Molecules, Chapman and Hall, New York, 1971.

3. P. Laszlo, Angew. Chemie Int. Ed., 2000, 39, 2071–2072.

4. H. C. Longuet-Higgins and R. P. Bell, J. Chem. Soc., 1943, 1, 250–255.

5. T. G. Dunne and N. W. Gregory, J. Am. Chem. Soc, 1958, 80, 1526–1530.