Talk:SL7514

JC: General comments: Well written report, code is very well commented and results look good. You show a good understanding of the background theory and nice idea to extend the analysis to compare with theoretical results from the literature, well done.

Report Info

DOI: DOI:10042/a3v2y

1. Introduction to the Ising Model

Task 1

The interaction energy is given by:

$E = - \frac{1}{2} J \sum_{i}^{N} \sum_{j \in n e i g h b o u r s (i)} s_{i} s_{j}$

where $s_{i} \in (- 1, 1)$

Since the spin can only be either +1 or -1 the first summation term will be maximum if all spins have the identical sign (i.e. $s_{i} = s_{j}$ then $s_{i} s_{j} = 1$ ). The number of neighbours each cell have is equal to 2D, where D is the dimension of the system (in one dimension each cell has two directly touching cells, in two dimension each cell has four directly touching cells etc). Therefore for the general case the minimum energy is given by:

$E = - \frac{1}{2} J \sum_{i}^{N} 2 D (1)$

$E = - \frac{1}{2} J (2 D N)$

$E = - D J N$

When all spins are pointing the same direction, there is only one distinguishable state where all spins pointing the same direction. Hence, multiplicity or W = 1. The Boltzmann entropy equation can be used to calculate the entropy:

$S = k_{B} \ln W$

$S_{0} = 1.38064 \times 1 0^{- 23} \times \ln 1 = 0$

v

Task 2

In three dimensions, each cell have 6 different interactions. When all spins are in the same direction the energy is given by:

$E_{a l i g n e d} = - D N J = - D (N - 1) J - 6 J$

JC: This isn't correct, check the maths. When you remove a spin by changing N to N-1, you are not removing the interactions of other spins with the spin that's been removed, in total you should remove 2DJ from the ground state to account for the interactions made by a single spin.

When one spin is flipped the energy is given by:

$E_{o n e f l i p} = - D (N - 1) J + 6 J$

Therefore, the difference in energy is given by:

$Δ E = E_{o n e f l i p} - E_{a l i g n e d} = - D (N - 1) J + 6 J - (- D (N - 1) J - 6 J)$

$Δ E = 6 J + 6 J = + 12 J$

JC: Correct answer, but check the maths in the working.

In three dimension, again the multiplicity is one when all spin points the same direction and hence the entropy is zero for the lowest energy state. When one spin is flipped there are 1000 different microstates as any one of the thousand cell can flip its spin. The multiplicity is then given by ^[1]:

$W = \frac{N!}{n_{1}! n_{2}!}$

where N = total number of ways the system can be arranged, $n_{1}$ is the number of flipped state and $n_{1}$ is the number of unflipped state. Hence

$W = \frac{1000!}{1! 999!} = 1000$

$S_{1} = k_{B} \ln 1000 = 9.537 \times 1 0^{- 23} J K^{- 1}$

$Δ S = S_{1} - S_{0} = + 9.537 \times 1 0^{- 23} J K^{- 1}$

JC: Correct.

Task 3

The magnetisation of 1D and 2D lattices are given by:

$M_{1 D} = 1$

$M_{2 D} = 1$

At absolute zero, the system will adopt the lowest energy configuration as there is no thermal energy available to overcome energy barriers. Therefore, the energy contribution will dominate the entropic contribution and all the spins will point the same direction. Therefore magnetisation will be 1000 since N = 1000.

JC: Correct.

2. Calculating the energy and magnetisation

The source code for the energy() function is shown below:

    def energy(self):
        "Return the total energy of the current lattice configuration."
        constant = -0.5
        energy = 0.0

        # double for loop: one loops through the rows and the other loops through the columns in 2D array
        for i in range(self.n_rows):
            for j in range(self.n_cols):
                # each cell receives an index
                index_1 = i
                index_2 = j
               
                # use index to find coordinates of the cell above, below, left and right to the cell of interest
                # there are four possible interactions for each cell in 2D lattice
                right = [index_1,index_2+1]
                left = [index_1,index_2-1]
                below = [index_1+1,index_2]
                above = [index_1-1,index_2]
                
                # implement periodic boundary conditions - negative array index automatically corresponds to last index but for the highest index values, there is a need to change the index to zero
                # if statement checks whether the cell is at the boundary and changes the index to zero
                if right[1] >= (self.n_cols):
                    right[1] = 0

                if below[0] >= (self.n_rows):
                    below[0] = 0
                
                # multiply the spins between the cells interacting
                interaction_right = (self.lattice[index_1][index_2])*(self.lattice[right[0]][right[1]])
                interaction_left = (self.lattice[index_1][index_2])*(self.lattice[left[0]][left[1]])
                interaction_above = (self.lattice[index_1][index_2])*(self.lattice[above[0]][above[1]])
                interaction_below = (self.lattice[index_1][index_2])*(self.lattice[below[0]][below[1]])

                # sum the four interaction for each cell and add to the cumulative energy variable
                local_sum = interaction_right + interaction_left + interaction_above + interaction_below
                energy = energy + local_sum + 0

        # divide by half to avoid double counting
        energy = energy * constant

        return energy

JC: Code looks good and is very well commented.

The source code for the magnetisation() function is given below:

    def magnetisation(self):
        "Return the total magnetisation of the current lattice configuration."
        magnetisation = 0.0
        for i in range(self.n_cols):
            for j in range(self.n_cols):
                magnetisation = magnetisation + self.lattice[j][i]
        return magnetisation

The output PNG image from running ILcheck.py file is given below:


The output image when ILcheck.py was ran

The code was tested for several random configurations and the image above was one of the performed test. From the tests it was observed that the Expected E and Actual E values were the same for minimum, random and maximum configurations suggesting that the code was running correctly.

3. Introduction to Monte Carlo Simulations

Task 1

Since each state has two possible configurations the multiplicity is given by:

$W = 2^{N}$

hence for 100 configurations

$W = 2^{100}$

The computation time is given by:

$t i m e = \frac{2^{100}}{1 \times 1 0^{9}} = 1.27 \times 1 0^{21} s$

JC: Correct, but can you convert this to more intuitive units - e.g. years?

Task 2

The implemented montecarlocycle(T) function is given below:

    def montecarlostep(self, T):
        # complete this function so that it performs a single Monte Carlo step
        energy_0 = self.energy()
        magnetisation_0 = self.magnetisation()

        #the following two lines will select the coordinates of the random spin for you
        random_i = np.random.choice(range(0, self.n_rows))
        random_j = np.random.choice(range(0, self.n_cols))        

        # copy initial lattice to a variable and flip one spin
        # unflipped_lattice = np.copy(self.lattice)
        self.lattice[random_i][random_j] = (self.lattice[random_i][random_j])*(-1)

        # find energy of the new lattice and calculate energy difference
        energy_1 = self.energy()
        magnetisation_1 = self.magnetisation()
        energy_difference = energy_1 - energy_0

       # implement part 4 of the algorithm
        if energy_difference <= 0:
            self.E = self.E + energy_1
            self.E2 = self.E2 + (energy_1)**2
            self.M = self.M + magnetisation_1
            self.M2 = self.M2 + (magnetisation_1)**2
            self.n_cycles = self.n_cycles + 1
            return energy_1, magnetisation_1

        if energy_difference > 0:
            #the following line will choose a random number in the rang e[0,1) for you
            random_number = np.random.random()
            transition_probability = math.exp(-energy_difference/T)

            # implement part 4 of the algorithm
            if random_number <= transition_probability:
                self.E = self.E + energy_1
                self.E2 = self.E2 + (energy_1)**2
                self.M = self.M + magnetisation_1
                self.M2 = self.M2 + (magnetisation_1)**2
                self.n_cycles = self.n_cycles + 1
                return energy_1, magnetisation_1

            # implement part 4 of the algorithm
            if random_number > transition_probability:
                self.E = self.E + energy_0
                self.E2 = self.E2 + (energy_0)**2
                self.M = self.M + magnetisation_0
                self.M2 = self.M2 + (magnetisation_0)**2
                self.n_cycles = self.n_cycles + 1
                self.lattice[random_i][random_j] = (self.lattice[random_i][random_j])*(-1)
                return energy_0, magnetisation_0

The implemented statistics function is given below:

    def statistics(self):
        # complete this function so that it calculates the correct values for the averages of E, E*E (E2), M, M*M (M2), and returns them
        E = self.E/self.n_cycles
        E2 = self.E2/self.n_cycles
        M = self.M/self.n_cycles
        M2 = self.M2/self.n_cycles
        return E, E2, M, M2, self.n_cycles

JC: Code looks correct.

Task 3

At lower temperature T< Tc, energy driving forces will dominate and the system will adopt the lowest energy configuration where the spins are all pointing in the same direction. Therefore the expected value for magnetisation will differ from 0 and the final magnetisation per spin will be either 1 or -1.

The output PNG image from running ILanim.py is given below:


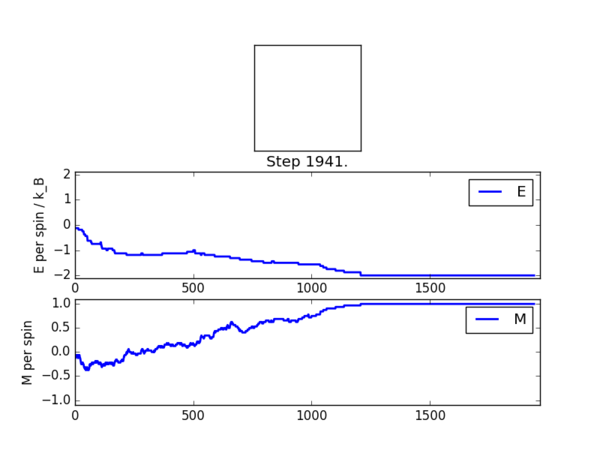
The output image when ILanim.py was ran at low T

The simulation above was performed at T=1 for 8x8 system size. Since the simulation was performed at a low temperature, the energy contribution dominates and hence the equilibrium configuration is the one in which all spins are parallel.


The output image when ILanim.py was ran at high T

The simulation above was performed at T=5 for 8x8 system size. Since the simulation was performed at a high temperature, the entropy contribution dominates and hence the equilibrium configuration is the one in which all spins are mixed. The entropy is maximised in this configuration as there are greater number of microstates available when the composition of spin up and spin down is closer to 50:50.

The output from the statistics() function is given below:

Averaged quantities:
E =  -1.58218809751
E*E =  2.70491194132
M =  0.627449808795
M*M =  0.584413838432

4. Accelerating the code

Task 1

Before optimisation
Trial number	Time taken for 2000 steps / s
1	10.2088440000000
2	10.2851739999999
3	10.1375520000000
4	10.2407219999999
5	10.0511209999999
6	10.1640249999999
7	10.0929270000000
8	10.1978689999999
9	10.2675140000000
mean	10.1828608888888
sample standard deviation	0.07884604
sample standard error	±0.024933307

Task 2

The energy() function after optimisation is given below:

    def energy(self):
        "Return the total energy of the current lattice configuration."
        energy = 0.0

        # create array shifted once upwards and to the left
        array_up = np.roll(self.lattice, 1, axis=0)
        array_left = np.roll(self.lattice, 1, axis=1)

        # multipy up and left array with the original array
        up_multiply = np.multiply(array_up, self.lattice)
        left_multipy = np.multiply(array_left, self.lattice)

        # sum the two multiplication together
        up_sum = float(np.sum(up_multiply))
        left_sum = float(np.sum(left_multipy))

        energy = (up_sum + left_sum)*(-1) + 0.0

        return energy

The magnetisation() function after optimisation is given below:

    def magnetisation(self):
        "Return the total magnetisation of the current lattice configuration."
        # simply sum the spins in the lattice
        magnetisation = float(np.sum(self.lattice))
        return magnetisation

JC: Good use of roll and multiply functions.

Task 3

After optimisation
Trial number	Time taken for 2000 steps / s
1	0.1340480000000
2	0.1425120000000
3	0.1443890000000
4	0.1430170000000
5	0.1419850000000
6	0.1477260000000
7	0.1402430000000
8	0.1423540000000
9	0.1408900000000
mean	0.1419071111111
sample standard deviation	0.003663881
sample standard error	±0.001158621

By comparing the two tables from Task 1 and Task 3, it can be seen that the time taken to compute 2000 steps has decreased after optimisation as mean ± standard error do not overlap. The double for loop was removed from the python code meaning the computer did not have to assign new values to the variables every time the code looped through the 2D array.

JC: The speed up is pretty significant - 2 orders of magnitude.

5. The effect of temperature

Task 1

In order to determine how many cycles were needed for the system to go from random starting position to equilibrium, different temperature and lattice sizes were tested. Equilibrium was reached when no further change in energy and magnetism value was observed (but the system may oscillate around the average value). During the test it was found that the larger lattice size led to greater equilibration time. Later in the script the largest lattice size investigated was 32x32 and hence N was determined using the 32x32 lattice. For the temperature, there were two possible regions which could have been used to determine N; above Tc and below Tc. When the temperature is above Tc, the system configuration changes from initially random to final random configuration whereas when the temperature is below Tc, the system configuration changes from initially random to ordered configuration. Therefore, it can be concluded that the equilibration time will be longer when the system changes from a random to an ordered configuration. Hence lowest temperature should be used to determine N where the system will equilibrate to completely ordered state. Furthermore, no oscillations were observed when T=0.25 was used and hence N could be determined with greater precision. Using the figures below, the final N was chosen to be 170000 (not precisely on 160000 to give some room for potential overshoots).

JC: Equilibration may be slowest for temperatures just below Tc rather than the lowest temperature, a long way below Tc.


The figure above shows system with lattice size 32x32 runtime 200000 at T=0.25	The figure above shows system with lattice size 32x32 runtime 200000 at T=1	The figure above shows system with lattice size 32x32 runtime 200000 at T=2

The figure above shows system with lattice size 32x32 runtime 200000 at T=3	The figure above shows system with lattice size 32x32 runtime 200000 at T=4	The figure above shows system with lattice size 32x32 runtime 200000 at T=5

The figure above shows system with lattice size 16x16 runtime 200000 at T=0.25

The modified montecarlostep() function is shown below:

    def montecarlostep(self, T):
        
        # complete this function so that it performs a single Monte Carlo step
        energy_0 = self.energy()
        magnetisation_0 = self.magnetisation()
        
        #the following two lines will select the coordinates of the random spin for you
        random_i = np.random.choice(range(0, self.n_rows))
        random_j = np.random.choice(range(0, self.n_cols))
        
        # copy initial lattice to a variable and flip one spin
        # unflipped_lattice = np.copy(self.lattice)
        self.lattice[random_i][random_j] = (self.lattice[random_i][random_j])*(-1)
        
        # find energy of the new lattice and calculate energy difference
        energy_1 = self.energy()
        magnetisation_1 = self.magnetisation()
        energy_difference = energy_1 - energy_0
        
        # check whether n_cycles is larger than N
        if self.n_cycles < self.N:

            if energy_difference <= 0:
                self.n_cycles = self.n_cycles + 1
                return energy_1, magnetisation_1

            if energy_difference > 0:
                random_number = np.random.random()
                transition_probability = math.exp(-energy_difference/T)
    
                if random_number <= transition_probability:
                    self.n_cycles = self.n_cycles + 1
                    return energy_1, magnetisation_1

                if random_number > transition_probability:
                    self.n_cycles = self.n_cycles + 1
                    self.lattice[random_i][random_j] = (self.lattice[random_i][random_j])*(-1)
                    return energy_0, magnetisation_0

        else:
        
            if energy_difference <= 0:
                self.E = self.E + energy_1
                self.E2 = self.E2 + (energy_1)**2
                self.M = self.M + magnetisation_1
                self.M2 = self.M2 + (magnetisation_1)**2
                self.n_cycles = self.n_cycles + 1
                return energy_1, magnetisation_1
        
            if energy_difference > 0:
                #the following line will choose a random number in the rang e[0,1) for you
                random_number = np.random.random()
                transition_probability = math.exp(-energy_difference/T)

                if random_number <= transition_probability:
                    self.E = self.E + energy_1
                    self.E2 = self.E2 + (energy_1)**2
                    self.M = self.M + magnetisation_1
                    self.M2 = self.M2 + (magnetisation_1)**2
                    self.n_cycles = self.n_cycles + 1
                    return energy_1, magnetisation_1

                if random_number > transition_probability:
                    self.E = self.E + energy_0
                    self.E2 = self.E2 + (energy_0)**2
                    self.M = self.M + magnetisation_0
                    self.M2 = self.M2 + (magnetisation_0)**2
                    self.n_cycles = self.n_cycles + 1
                    self.lattice[random_i][random_j] = (self.lattice[random_i][random_j])*(-1)
                    return energy_0, magnetisation_0

The modified statistics() function is shown below:

    def statistics(self):
        # complete this function so that it calculates the correct values for the averages of E, E*E (E2), M, M*M (M2), and returns them
        E = self.E/(self.n_cycles - self.N)
        E2 = self.E2/(self.n_cycles - self.N)
        M = self.M/(self.n_cycles - self.N)
        M2 = self.M2/(self.n_cycles - self.N)
        

        return E, E2, M, M2, self.n_cycles

JC: Good choice of number of steps to ignore to allow for equilibration and well implemented in code.

Task 2

For the final simulations performed in ILfinalframe.py, the total number of time-step was chosen to be 500000 with N = 170000 for 8x8 lattice size. This choice meant that there were plenty of time-steps between 170000 and 500000 to take average values from. Temperature spacing of 0.01 was used since when smaller the spacing was used, more accurately the variations in energy and magnetisation were captured. The plots with error bars are shown later in this section.


The plot above shows the plot of average energy for each temperature with 0.01 temperature spacing			The plot above shows the plot of average magnetisation for each temperature with 0.01 temperature spacing

The matplotlib source code for the plot of average energy for each temperature with 0.01 temperature spacing is given below

# energy vs temperature plot for 8x8 with error bars large intervals
# color scheme generated using html color codes from webpage http://htmlcolorcodes.com/
  
 %pylab inline
 import numpy as np
  
 data = np.loadtxt("8x8_trial_1.dat", delimiter=' ')
  
 T = data[:,0]
 E = data[:,1]
  
 # change list to array
 T_array = np.array(T)
 E_array = np.array(E)
  
 figure(figsize=(8,5))
  
 font = {'size'   : 16}
  
 # plot using matplotlib
 matplotlib.rc('font', **font)
  
 ax = gca()
 ax.spines['right'].set_linewidth(3)
 ax.spines['top'].set_linewidth(3)
 ax.spines['bottom'].set_linewidth(3)
 ax.spines['left'].set_linewidth(3)
 ax.xaxis.set_ticks_position('bottom')
 ax.yaxis.set_ticks_position('left')
  
 grid(b=True, which='major', color='grey', linestyle='--')
  
 xlabel('Temperature', fontsize=16, fontweight='bold')
 ylabel('Energy per spin', fontsize=16, fontweight='bold')
 plt.title('A plot of energy per spin vs temperature \n for 8x8 system size small timestep', fontsize=16, fontweight='bold')
  
  
 ttl = ax.title
 ttl.set_position([.5, 1.05])
  
 plot(T_array, E_array, color="#CB4335", label="Energy", linewidth=3)
  
 show()

The matplotlib source code for the plot of average magnetisation for each temperature with 0.01 temperature spacing is given below

# energy vs magnetisation plot for 8x8 with error bars small intervals
# color scheme generated using html color codes from webpage http://htmlcolorcodes.com/
  
 %pylab inline
 import numpy as np
  
 data = np.loadtxt("8x8_trial_1.dat", delimiter=' ')
  
 T = data[:,0]
 M = data[:,3]
  
 # change list to array
 T_array = np.array(T)
 M_array = np.array(M)
  
 figure(figsize=(8,5))
  
 font = {'size'   : 16}
  
 # plot using matplotlib
 matplotlib.rc('font', **font)
  
 ax = gca()
 ax.spines['right'].set_linewidth(3)
 ax.spines['top'].set_linewidth(3)
 ax.spines['bottom'].set_linewidth(3)
 ax.spines['left'].set_linewidth(3)
 ax.xaxis.set_ticks_position('bottom')
 ax.yaxis.set_ticks_position('left')
  
 grid(b=True, which='major', color='grey', linestyle='--')
  
 xlabel('Temperature', fontsize=16, fontweight='bold')
 ylabel('Magnetisation per spin', fontsize=16, fontweight='bold')
 plt.title('A plot of magnetisation per spin vs temperature \n for 8x8 system size small timestep', fontsize=16, fontweight='bold')
  
  
 ttl = ax.title
 ttl.set_position([.5, 1.05])
  
 plot(T_array, M_array, color="#229954", label="Energy", linewidth=3)
  
 show()


The plot below shows the plot of average energy for each temperature with 0.25 temperature spacing with error bars. The temperature spacing was reduced so the error bars can be seen more clearly.			The plot below shows the plot of average magnetisation for each temperature with 0.25 temperature spacing with error bars. The temperature spacing was reduced so the error bars can be seen more clearly.

From the two plots above, it was obvious that as temperature increased, the error in average energy and magnetisation increased. At higher temperatures greater fluctuations around the average values of energy and magnetisation were observed which increased the standard deviations in the averaged values.

The matplotlib source code for the plot of average energy for each temperature with 0.25 temperature spacing with error bars is given below

# energy vs temperature plot for 8x8 with error bars large intervals
# color scheme generated using html color codes from webpage http://htmlcolorcodes.com/
  
 %pylab inline
 import numpy as np
  
 data = np.loadtxt("8x8_trial_2.dat", delimiter=' ')
  
 T = data[:,0]
 E = data[:,1]
 all_stdev = []
  
 # loop through each line in the text file and calculate the standard deviation
for line in data:
    E2 = line[2]
     E_in = line[1]
     stdev = sqrt((E2) - (E_in)**2)
     all_stdev = all_stdev + [stdev]
  
 # change list to array
 T_array = np.array(T)
 E_array = np.array(E)
  
 figure(figsize=(8,5))
  
 font = {'size'   : 16}
  
 # plot using matplotlib
 matplotlib.rc('font', **font)
  
 ax = gca()
 ax.spines['right'].set_linewidth(3)
 ax.spines['top'].set_linewidth(3)
 ax.spines['bottom'].set_linewidth(3)
 ax.spines['left'].set_linewidth(3)
 ax.xaxis.set_ticks_position('bottom')
 ax.yaxis.set_ticks_position('left')
  
 grid(b=True, which='major', color='grey', linestyle='--')
  
 xlabel('Temperature', fontsize=16, fontweight='bold')
 ylabel('Energy per spin', fontsize=16, fontweight='bold')
 plt.title('A plot of energy per spin vs temperature \n for 8x8 system size large timestep', fontsize=16, fontweight='bold')
  
  
 ttl = ax.title
 ttl.set_position([.5, 1.05])
  
 scatter(T_array, E_array, color="#CB4335", label="Energy", linewidth=3)
 plt.errorbar(T_array, E_array, yerr=all_stdev, color='#CB4335', linewidth=3)
  
 # legend(loc="upper left")
  
 show()

The matplotlib source code for the plot of average magnetisation for each temperature with 0.25 temperature spacing with error bars

# energy vs magnetisation plot for 8x8 with error bars large intervals
# color scheme generated using html color codes from webpage http://htmlcolorcodes.com/
  
 %pylab inline
 import numpy as np
  
 data = np.loadtxt("8x8_trial_2.dat", delimiter=' ')
  
 T = data[:,0]
 M = data[:,3]
 all_stdev = []
  
 # loop through each line in the text file and calculate the standard deviation
for line in data:
    M2 = line[4]
     M_in = line[3]
     stdev = sqrt((M2) - (M_in)**2)
     all_stdev = all_stdev + [stdev]
  
 # change list to array
 T_array = np.array(T)
 M_array = np.array(M)
  
 figure(figsize=(8,5))
  
 font = {'size'   : 16}
  
 # plot using matplotlib
 matplotlib.rc('font', **font)
  
 ax = gca()
 ax.spines['right'].set_linewidth(3)
 ax.spines['top'].set_linewidth(3)
 ax.spines['bottom'].set_linewidth(3)
 ax.spines['left'].set_linewidth(3)
 ax.xaxis.set_ticks_position('bottom')
 ax.yaxis.set_ticks_position('left')
  
 grid(b=True, which='major', color='grey', linestyle='--')
 
 xlabel('Temperature', fontsize=16, fontweight='bold')
 ylabel('Magnetisation per spin', fontsize=16, fontweight='bold')
 plt.title('A plot of magnetisation per spin vs temperature \n for 8x8 system size large timestep', fontsize=16, fontweight='bold')
  
  
 ttl = ax.title
 ttl.set_position([.5, 1.05])
  
 plt.scatter(T_array, M_array, color="#229954", label="Energy", linewidth=3)
 plt.errorbar(T_array, M_array, yerr=all_stdev, color='#229954', linewidth=3)
  
 # legend(loc="upper left")
  
 show()

6. Effect of system size

Task 1


The plot above outlines the variations in energy with temperature for five different system sizes.			The plot above outlines the variations in magnetism with temperature for five different system sizes.

It can be seen from the energy plots that at low temperature the system prefers to exist with all spins aligned. However, as the temperature is increased, a phase transition is observed and the system preferentially exist in state which maximises entropy. From the energy plots above, the curvature of the graph became more clearly defined as the lattice size increased. There isn't a precise difference between the curves for 16x16 and 32x32 lattice sizes meaning that 16x16 was good enough to capture the long range interactions. It should also be noted that the first derivative of the energy vs temperature was continuous for all system sizes meaning the second order phase transition was taking place at Tc ^[2].

The magnetisation plots also followed the expected trend; as the temperature was increased, the system preferred to exist in 50:50 spin up and spin down configurations and hence the total magnetisation decreased to zero. However, it can be seen that the curvature of the graphs became more clearly defined as the system size was increased. In contrast to the plots from energy vs temperature, the largest system size 32x32 illustrated far better continuous phase transition compared to 16x16 system size. Therefore, it was concluded that the 32x32 system size most accurately reproduced the expected behaviour of the system. Furthermore, for small system sizes 2x2, 4x4, and 8x8, the curie temperature was not accurately reproduced from magnetisation vs temperature plot. The curie temperature is the point where the magnetisation plot start to oscillate around zero. Compare the location of Tc from the magnetisation plot above to the heat capacity vs temperature plot later in this report. The peak heat capacity all occurred within the temperature range 2-3 but in the magnetisation plot the Tc occurred below 2 for small lattice sizes. When the system size was very small, one spin flip will affect the entire system. In comparison, when the system size is large, when one spin flip occurs, there are many intermediate interactions which must occur before the cell on the other side of the lattice is affected. Therefore, small system sizes do not reproduce the behaviour of the real system and hence contradictory pattern was observed in the magnetisation plot above.

JC: Well noticed that the trend in Curie temperature with system size in the magnetisation graph seems to contradict the trend from the heat capacity graph. In small systems a single spin flip can more easily force the entire lattice to flip from a fully up to fully down state.

It will be shown later in this report that the point of the steepest gradient in Energy vs Temperature plot corresponds to the Curie Temperature.

The python code used to generate the plot outlining the variations in energy with temperature for five different system sizes using matplotlib is shown below:

# energy vs temperature plot for all system sizes
# color scheme generated using html color codes from webpage http://htmlcolorcodes.com/
  
 %pylab inline
 import numpy as np
  
 a2x2 = np.loadtxt("2x2_trial_1.dat", delimiter=' ')
 a4x4 = np.loadtxt("4x4_trial_1.dat", delimiter=' ')
 a8x8 = np.loadtxt("8x8_trial_1.dat", delimiter=' ')
 a16x16 = np.loadtxt("16x16_trial_1.dat", delimiter=' ')
 a32x32 = np.loadtxt("32x32_trial_1.dat", delimiter=' ')
  
 # load each data for different system sizes to a new list

T2x2 = a2x2[:,0]
E2x2 = a2x2[:,1]
newE2x2 = [x/4 for x in E2x2]

T4x4 = a4x4[:,0]
E4x4 = a4x4[:,1]
newE4x4 = [x/16 for x in E4x4]

T8x8 = a8x8[:,0]
E8x8 = a8x8[:,1]
newE8x8 = [x/64 for x in E8x8]

T16x16 = a16x16[:,0]
E16x16 = a16x16[:,1]
newE16x16 = [x/256 for x in E16x16]

T32x32 = a32x32[:,0]
E32x32 = a32x32[:,1]
newE32x32 = [x/1024 for x in E32x32]

# change list to array
  
 T2x2_array = np.array(T2x2)
 E2x2_array = np.array(newE2x2)
  
 T4x4_array = np.array(T4x4)
 E4x4_array = np.array(newE4x4)
  
 T8x8_array = np.array(T8x8)
 E8x8_array = np.array(newE8x8)
  
 T16x16_array = np.array(T16x16)
 E16x16_array = np.array(newE16x16)
  
 T32x32_array = np.array(T32x32)
 E32x32_array = np.array(newE32x32)
  
 figure(figsize=(8,5))
  
 font = {'size'   : 16}
  
 # plot using matplotlib
  
 matplotlib.rc('font', **font)
  
 ax = gca()
 ax.spines['right'].set_linewidth(3)
 ax.spines['top'].set_linewidth(3)
 ax.spines['bottom'].set_linewidth(3)
 ax.spines['left'].set_linewidth(3)
 ax.xaxis.set_ticks_position('bottom')
 ax.yaxis.set_ticks_position('left')
  
 grid(b=True, which='major', color='grey', linestyle='--')
  
 xlabel('Temperature', fontsize=16, fontweight='bold')
 ylabel('Energy per spin', fontsize=16, fontweight='bold')
 plt.title('A plot of energy per spin vs temperature \n for all system sizes', fontsize=16, fontweight='bold')
 ylim(-2.2, -0.2)
  
 ttl = ax.title
 ttl.set_position([.5, 1.05])
  
 plot(T2x2_array, E2x2_array, color="#2E86C1", label="2x2", linewidth=3)
 plot(T4x4_array, E4x4_array, color="#138D75", label="4x4", linewidth=3)
 plot(T8x8_array, E8x8_array, color="#D68910", label="8x8", linewidth=3)
 plot(T16x16_array, E16x16_array, color="#C0392B", label="16x16", linewidth=3)
 plot(T32x32_array, E32x32_array, color="#7D3C98", label="32x32", linewidth=3)
  
 legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0., prop={'size':10})
  
 show()

The python code used to generate the plot to show the variations in magnetism with temperature for five different system sizes using matplotlib is shown below:

# magnetisation vs temperature plot for all system sizes
# color scheme generated using html color codes from webpage http://htmlcolorcodes.com/
 
 %pylab inline
 import numpy as np
 
 a2x2 = np.loadtxt("2x2_trial_1.dat", delimiter=' ')
 a4x4 = np.loadtxt("4x4_trial_1.dat", delimiter=' ')
 a8x8 = np.loadtxt("8x8_trial_1.dat", delimiter=' ')
 a16x16 = np.loadtxt("16x16_trial_1.dat", delimiter=' ')
 a32x32 = np.loadtxt("32x32_trial_1.dat", delimiter=' ')
 
 # load each data for different system sizes to a new list

T2x2 = a2x2[:,0]
M2x2 = a2x2[:,3]
newM2x2 = [x/4 for x in M2x2]

T4x4 = a4x4[:,0]
M4x4 = a4x4[:,3]
newM4x4 = [x/16 for x in M4x4]

T8x8 = a8x8[:,0]
M8x8 = a8x8[:,3]
newM8x8 = [x/64 for x in M8x8]

T16x16 = a16x16[:,0]
M16x16 = a16x16[:,3]
newM16x16 = [x/256 for x in M16x16]

T32x32 = a32x32[:,0]
M32x32 = a32x32[:,3]
newM32x32 = [x/1024 for x in M32x32]

# change list to array
 
 T2x2_array = np.array(T2x2)
 M2x2_array = np.array(newM2x2)
 
 T4x4_array = np.array(T4x4)
 M4x4_array = np.array(newM4x4)
 
 T8x8_array = np.array(T8x8)
 M8x8_array = np.array(newM8x8)
 
 T16x16_array = np.array(T16x16)
 M16x16_array = np.array(newM16x16)
 
 T32x32_array = np.array(T32x32)
 M32x32_array = np.array(newM32x32)
 
 figure(figsize=(8,5))
 
 font = {'size'   : 16}
 
 # plot using matplotlib
 
 matplotlib.rc('font', **font)
 
 ax = gca()
 ax.spines['right'].set_linewidth(3)
 ax.spines['top'].set_linewidth(3)
 ax.spines['bottom'].set_linewidth(3)
 ax.spines['left'].set_linewidth(3)
 ax.xaxis.set_ticks_position('bottom')
 ax.yaxis.set_ticks_position('left')
 
 grid(b=True, which='major', color='grey', linestyle='--')
 
 xlabel('Temperature', fontsize=16, fontweight='bold')
 ylabel('Magnetisation per spin', fontsize=16, fontweight='bold')
 plt.title('A plot of magnetisation per spin vs temperature \n for all system sizes', fontsize=16, fontweight='bold')
 ylim(-1.1, 1.1)
 
 ttl = ax.title
 ttl.set_position([.5, 1.05])
 
 plot(T2x2_array, M2x2_array, color="#2E86C1", label="2x2", linewidth=1)
 plot(T4x4_array, M4x4_array, color="#138D75", label="4x4", linewidth=1)
 plot(T8x8_array, M8x8_array, color="#D68910", label="8x8", linewidth=1)
 plot(T16x16_array, M16x16_array, color="#C0392B", label="16x16", linewidth=1)
 plot(T32x32_array, M32x32_array, color="#7D3C98", label="32x32", linewidth=1)
 
 legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0., prop={'size':10})
 
 show()

For clarity, magnetisation per spin vs temperature plot is shown for the individual system sizes below:


The plot above outlines the variations in magnetism with temperature for 2x2 system size.	The plot above outlines the variations in magnetism with temperature for 4x4 system size.	The plot above outlines the variations in magnetism with temperature for 8x8 system size.

The plot above outlines the variations in magnetism with temperature for 16x16 system size.	The plot above outlines the variations in magnetism with temperature for 32x32 system size.

The python source code used to generate the figure for the 2x2 system size magnetism is shown below:

# magnetisation vs temperature plot for 2x2 system sizes
# color scheme generated using html color codes from webpage http://htmlcolorcodes.com/
 
 %pylab inline
 import numpy as np
 
 a2x2 = np.loadtxt("2x2_trial_1.dat", delimiter=' ')
 
 T2x2 = a2x2[:,0]
 M2x2 = a2x2[:,3]
 newM2x2 = [x/4 for x in M2x2]
 
 # change list to array
 
 T2x2_array = np.array(T2x2)
 M2x2_array = np.array(newM2x2)
 
 figure(figsize=(8,5))
 
 font = {'size'   : 16}
 
 # plot using matplotlib
 
 matplotlib.rc('font', **font)
 
 ax = gca()
 ax.spines['right'].set_linewidth(3)
 ax.spines['top'].set_linewidth(3)
 ax.spines['bottom'].set_linewidth(3)
 ax.spines['left'].set_linewidth(3)
 ax.xaxis.set_ticks_position('bottom')
 ax.yaxis.set_ticks_position('left')
 
 grid(b=True, which='major', color='grey', linestyle='--')
 
 xlabel('Temperature', fontsize=16, fontweight='bold')
 ylabel('Magnetisation per spin', fontsize=16, fontweight='bold')
 plt.title('A plot of magnetisation per spin vs temperature \n for 2x2 system size', fontsize=16, fontweight='bold')
 ylim(-1.1, 1.1)
 
 ttl = ax.title
 ttl.set_position([.5, 1.05])
 
 plot(T2x2_array, M2x2_array, color="#2E86C1", label="2x2", linewidth=1)
 
 show()

The python source code used to generate the figure for 4x4 system size magnetism above is shown below:

 magnetisation vs temperature plot for 4x4 system sizes
# color scheme generated using html color codes from webpage http://htmlcolorcodes.com/
 
 %pylab inline
 import numpy as np
 
 a4x4 = np.loadtxt("4x4_trial_1.dat", delimiter=' ')
 
 T4x4 = a4x4[:,0]
 M4x4 = a4x4[:,3]
 newM4x4 = [x/16 for x in M4x4]
 
 # change list to array
 
 T4x4_array = np.array(T4x4)
 M4x4_array = np.array(newM4x4)
 
 figure(figsize=(8,5))
 
 font = {'size'   : 16}
 
 # plot using matplotlib
 
 matplotlib.rc('font', **font)
 
 ax = gca()
 ax.spines['right'].set_linewidth(3)
 ax.spines['top'].set_linewidth(3)
 ax.spines['bottom'].set_linewidth(3)
 ax.spines['left'].set_linewidth(3)
 ax.xaxis.set_ticks_position('bottom')
 ax.yaxis.set_ticks_position('left')
 
 grid(b=True, which='major', color='grey', linestyle='--')
 
 xlabel('Temperature', fontsize=16, fontweight='bold')
 ylabel('Magnetisation per spin', fontsize=16, fontweight='bold')
 plt.title('A plot of magnetisation per spin vs temperature \n for 4x4 system size', fontsize=16, fontweight='bold')
 ylim(-1.1, 1.1)
 
 ttl = ax.title
 ttl.set_position([.5, 1.05])
 
 plot(T4x4_array, M4x4_array, color="#138D75", label="4x4", linewidth=1)
 
 show()

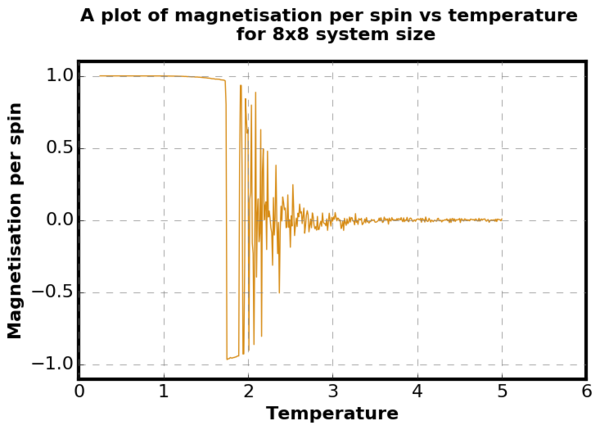
The python source code used to generate the figure for 8x8 system size magnetism above is shown below:

# magnetisation vs temperature plot for 8x8 system sizes
# color scheme generated using html color codes from webpage http://htmlcolorcodes.com/
 
 %pylab inline
 import numpy as np
 
 a8x8 = np.loadtxt("8x8_trial_1.dat", delimiter=' ')
 
 T8x8 = a8x8[:,0]
 M8x8 = a8x8[:,3]
 newM8x8 = [x/64 for x in M8x8]
 
 # change list to array
 
 T8x8_array = np.array(T8x8)
 M8x8_array = np.array(newM8x8)
 
 figure(figsize=(8,5))
 
 font = {'size'   : 16}
 
 # plot using matplotlib
 
 matplotlib.rc('font', **font)
 
 ax = gca()
 ax.spines['right'].set_linewidth(3)
 ax.spines['top'].set_linewidth(3)
 ax.spines['bottom'].set_linewidth(3)
 ax.spines['left'].set_linewidth(3)
 ax.xaxis.set_ticks_position('bottom')
 ax.yaxis.set_ticks_position('left')
 
 grid(b=True, which='major', color='grey', linestyle='--')
 
 xlabel('Temperature', fontsize=16, fontweight='bold')
 ylabel('Magnetisation per spin', fontsize=16, fontweight='bold')
 plt.title('A plot of magnetisation per spin vs temperature \n for 8x8 system size', fontsize=16, fontweight='bold')
 ylim(-1.1, 1.1)
 
 ttl = ax.title
 ttl.set_position([.5, 1.05])
 
 plot(T8x8_array, M8x8_array, color="#D68910", label="8x8", linewidth=1)
 
 show()

The python source code used to generate the figure for 16x16 system size above is shown below:

# magnetisation vs temperature plot for 16x16 system sizes
# color scheme generated using html color codes from webpage http://htmlcolorcodes.com/
 
 %pylab inline
 import numpy as np
 
 a16x16 = np.loadtxt("16x16_trial_1.dat", delimiter=' ')
 
 T16x16 = a16x16[:,0]
 M16x16 = a16x16[:,3]
 newM16x16 = [x/256 for x in M16x16]
 
 # change list to array
 
 T16x16_array = np.array(T16x16)
 M16x16_array = np.array(newM16x16)
 
 figure(figsize=(8,5))
 
 font = {'size'   : 16}
 
 # plot using matplotlib
 
 matplotlib.rc('font', **font)
 
 ax = gca()
 ax.spines['right'].set_linewidth(3)
 ax.spines['top'].set_linewidth(3)
 ax.spines['bottom'].set_linewidth(3)
 ax.spines['left'].set_linewidth(3)
 ax.xaxis.set_ticks_position('bottom')
 ax.yaxis.set_ticks_position('left')
 
 grid(b=True, which='major', color='grey', linestyle='--')
 
 xlabel('Temperature', fontsize=16, fontweight='bold')
 ylabel('Magnetisation per spin', fontsize=16, fontweight='bold')
 plt.title('A plot of magnetisation per spin vs temperature \n for 16x16 system size', fontsize=16, fontweight='bold')
 ylim(-1.1, 1.1)
 
 ttl = ax.title
 ttl.set_position([.5, 1.05])
 
 plot(T16x16_array, M16x16_array, color="#C0392B", label="16x16", linewidth=1)
 
 show()

The python source code used to generate the figure for 32x23 system size magnetism above is shown below:

# magnetisation vs temperature plot for 32x32 system sizes
# color scheme generated using html color codes from webpage http://htmlcolorcodes.com/
 
 %pylab inline
 import numpy as np
 
 a32x32 = np.loadtxt("32x32_trial_1.dat", delimiter=' ')
 
 T32x32 = a32x32[:,0]
 M32x32 = a32x32[:,3]
 newM32x32 = [x/1024 for x in M32x32]
 
 # change list to array
 
 T32x32_array = np.array(T32x32)
 M32x32_array = np.array(newM32x32)
 
 figure(figsize=(8,5))
 
 font = {'size'   : 16}
 
 # plot using matplotlib
 
 matplotlib.rc('font', **font)
 
 ax = gca()
 ax.spines['right'].set_linewidth(3)
 ax.spines['top'].set_linewidth(3)
 ax.spines['bottom'].set_linewidth(3)
 ax.spines['left'].set_linewidth(3)
 ax.xaxis.set_ticks_position('bottom')
 ax.yaxis.set_ticks_position('left')
 
 grid(b=True, which='major', color='grey', linestyle='--')
 
 xlabel('Temperature', fontsize=16, fontweight='bold')
 ylabel('Magnetisation per spin', fontsize=16, fontweight='bold')
 plt.title('A plot of magnetisation per spin vs temperature \n for 32x32 system size', fontsize=16, fontweight='bold')
 ylim(-1.1, 1.1)
 
 ttl = ax.title
 ttl.set_position([.5, 1.05])
 
 plot(T32x32_array, M32x32_array, color="#7D3C98", label="16x16", linewidth=1)
 
 show()

JC: All code looks well laid out and is well commented.

7. Determining the Heat Capacity

Task 1

The derivation for the heat capacity equation is outlined below ^[3]:

$⟨ E ⟩ = \sum_{α} E_{α} P (E_{α}) = \frac{\sum_{α} E_{α} e^{- β T}}{\sum_{α} e^{- β T}}$

$⟨ E^{2} ⟩ = \sum_{α} E_{α}^{2} P (E_{α}) = \frac{\sum_{α} E_{α}^{2} e^{- β T}}{\sum_{α} e^{- β T}}$

$V a r (E) = ⟨ E^{2} ⟩ - {(⟨ E ⟩)}^{2}$

where

$P (E_{α}) = \frac{e^{- \frac{E_{α}}{k_{B}}}}{\sum_{α} e^{- \frac{E_{α}}{k_{B} T}}} = \frac{e^{- β T}}{\sum_{α} e^{- β T}}$

$β = \frac{1}{k_{B} T}$

$C_{v} = \frac{\partial ⟨ E ⟩}{\partial T} = \frac{\partial β}{\partial T} \frac{\partial ⟨ E ⟩}{\partial β} = - \frac{β}{T} \frac{\partial ⟨ E ⟩}{\partial β}$

$C_{v} = - \frac{β}{T} \frac{\partial}{\partial β} (\frac{\sum_{α} E_{α} e^{- β T}}{\sum_{α} e^{- β T}})$

Using quotient rule:

$C_{v} = - \frac{β}{T} \frac{- \sum_{α} E_{α}^{2} e^{- β E_{α}} \sum_{α} e^{- β E_{α}} + {(\sum_{α} E_{α} e^{- β E α})}^{2}}{{(\sum_{α} e^{- β E_{α}})}^{2}}$

$C_{v} = \frac{β}{T} [\frac{\sum_{α} E_{α}^{2} e^{- β E_{α}} \sum_{α} e^{- β E_{α}}}{{(\sum_{α} e^{- β E_{α}})}^{2}} - {(\frac{\sum_{α} E_{α} e^{- β E α}}{\sum_{α} e^{- β E_{α}}})}^{2}]$

$C_{v} = \frac{β}{T} [(\frac{\sum_{α} E_{α}^{2} e^{- β E_{α}}}{\sum_{α} e^{- β E_{α}}}) - {(\frac{\sum_{α} E_{α} e^{- β E α}}{\sum_{α} e^{- β E_{α}}})}^{2}]$

$C_{v} = \frac{β}{T} [⟨ E^{2} ⟩ - {(⟨ E ⟩)}^{2}]$

$C_{v} = \frac{V a r (E)}{k_{B} T^{2}}$

JC: Good derivation, but be careful with notation, the Boltzmann factor in the average energy should be exp(E_alpha*beta) not exp(T*beta).

Task 2

The plot below shows heat capacity vs temperature plots for all five lattice sizes:


The plot above outlines the variations in heat capacity per spin with temperature for five different system sizes.

There were few interesting trends which were identified from the plots above. Firstly, no divergence were observed for all plots which is characteristic of second order phase transitions. This was due to the limitation of the model as no investigation was performed at the infinite lattice. The usage of periodic boundary condition minimises the effect and it can be seen that as the system size increases, the shape of the curve became more increasingly sharpened. The original paper by Onsager ^[4] also outlines this phenomenon where it is stated that for a finite crystal, the heat capacity is expected to be finite at all temperatures. Furthermore, the critical temperature decreased as the system size increased. The Energy vs Temperature plots showed that the location of the steepest gradient occurred at lower temperature which agreed with the observed trend. The peak heat capacity also increased with increasing system size. This result was also consistent with the original paper by Onsager and is discussed further in the extension section 9. Intuitively this observation was agin in agreement with Energy vs Temperature plots as the value of the steepest gradient increased with the increasing system size.

The python source code for the plot above is shown below:

# heat capacity vs temperature plot for all system sizes
# color scheme generated using html color codes from webpage http://htmlcolorcodes.com/
 
 %pylab inline
 import numpy as np
 
 a2x2 = np.loadtxt("2x2_trial_1.dat", delimiter=' ')
 a4x4 = np.loadtxt("4x4_trial_1.dat", delimiter=' ')
 a8x8 = np.loadtxt("8x8_trial_1.dat", delimiter=' ')
 a16x16 = np.loadtxt("16x16_trial_1.dat", delimiter=' ')
 a32x32 = np.loadtxt("32x32_trial_1.dat", delimiter=' ')
 
 # load each data for different system sizes to a new list

T2x2 = a2x2[:,0]
hc2x2 = []
for line in a2x2:
    temperature = line[0]
     energy = line[1]
     energy2 = line[2]
     system_size = 4
     heat_capacity = ((energy2) - (energy)**2)/((temperature**2)*(system_size))
    hc2x2 = hc2x2 + [heat_capacity]
     
 T4x4 = a4x4[:,0]
 hc4x4 = []
 for line in a4x4:
     temperature = line[0]
     energy = line[1]
     energy2 = line[2]
     system_size = 16
     heat_capacity = ((energy2) - (energy)**2)/((temperature**2)*(system_size))
    hc4x4 = hc4x4 + [heat_capacity]
 
 T8x8 = a8x8[:,0]
 hc8x8 = []
 for line in a8x8:
     temperature = line[0]
     energy = line[1]
     energy2 = line[2]
     system_size = 64
     heat_capacity = ((energy2) - (energy)**2)/((temperature**2)*(system_size))
    hc8x8 = hc8x8 + [heat_capacity]
 
 T16x16 = a16x16[:,0]
 hc16x16 = []
 for line in a16x16:
     temperature = line[0]
     energy = line[1]
     energy2 = line[2]
     system_size = 256
     heat_capacity = ((energy2) - (energy)**2)/((temperature**2)*(system_size))
    hc16x16 = hc16x16 + [heat_capacity]
 
 T32x32 = a32x32[:,0]
 hc32x32 = []
 for line in a32x32:
     temperature = line[0]
     energy = line[1]
     energy2 = line[2]
     system_size = 1024
     heat_capacity = ((energy2) - (energy)**2)/((temperature**2)*(system_size))
    hc32x32 = hc32x32 + [heat_capacity]
 
 # change list to array
 
 T2x2_array = np.array(T2x2)
 hc2x2_array = np.array(hc2x2)
 
 T4x4_array = np.array(T4x4)
 hc4x4_array = np.array(hc4x4)
 
 T8x8_array = np.array(T8x8)
 hc8x8_array = np.array(hc8x8)
 
 T16x16_array = np.array(T16x16)
 hc16x16_array = np.array(hc16x16)
 
 T32x32_array = np.array(T32x32)
 hc32x32_array = np.array(hc32x32)
 
 figure(figsize=(8,5))
 
 font = {'size'   : 16}
 
 # plot using matplotlib
 
 matplotlib.rc('font', **font)
 
 ax = gca()
 ax.spines['right'].set_linewidth(3)
 ax.spines['top'].set_linewidth(3)
 ax.spines['bottom'].set_linewidth(3)
 ax.spines['left'].set_linewidth(3)
 ax.xaxis.set_ticks_position('bottom')
 ax.yaxis.set_ticks_position('left')
 
 grid(b=True, which='major', color='grey', linestyle='--')
 
 xlabel('Temperature', fontsize=16, fontweight='bold')
 ylabel('heat capacity per spin', fontsize=16, fontweight='bold')
 plt.title('A plot of heat capacity per spin vs temperature \n for all system sizes', fontsize=16, fontweight='bold')
 
 ttl = ax.title
 ttl.set_position([.5, 1.05])
 
 plot(T2x2_array, hc2x2_array, color="#2E86C1", label="2x2", linewidth=1)
 plot(T4x4_array, hc4x4_array, color="#138D75", label="4x4", linewidth=1)
 plot(T8x8_array, hc8x8_array, color="#D68910", label="8x8", linewidth=1)
 plot(T16x16_array, hc16x16_array, color="#C0392B", label="16x16", linewidth=1)
 plot(T32x32_array, hc32x32_array, color="#7D3C98", label="32x32", linewidth=1)
 
 legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0., prop={'size':10})
 
 show()

For clarity, the individual plots for each lattice sizes are illustrated below:


A plot showing heat capacity vs spin for 2x2 system size	A plot showing heat capacity vs spin for 4x4 system size	A plot showing heat capacity vs spin for 8x8 system size

A plot showing heat capacity vs spin for 16x16 system size	A plot showing heat capacity vs spin for 32x32 system size

The python source code for 2x2 plot is shown below:

# heat capacity vs temperature plot for 2x2 system size
# color scheme generated using html color codes from webpage http://htmlcolorcodes.com/
 
 %pylab inline
 import numpy as np
 
 a2x2 = np.loadtxt("2x2_trial_1.dat", delimiter=' ')
 
 # load each data for different system sizes to a new list

T2x2 = a2x2[:,0]
hc2x2 = []
for line in a2x2:
    temperature = line[0]
     energy = line[1]
     energy2 = line[2]
     system_size = 4
     heat_capacity = ((energy2) - (energy)**2)/((temperature**2)*(system_size))
    hc2x2 = hc2x2 + [heat_capacity]
 
 # change list to array
 
 T2x2_array = np.array(T2x2)
 hc2x2_array = np.array(hc2x2)
 
 figure(figsize=(8,5))
 
 font = {'size'   : 16}
 
 # plot using matplotlib
 
 matplotlib.rc('font', **font)
 
 ax = gca()
 ax.spines['right'].set_linewidth(3)
 ax.spines['top'].set_linewidth(3)
 ax.spines['bottom'].set_linewidth(3)
 ax.spines['left'].set_linewidth(3)
 ax.xaxis.set_ticks_position('bottom')
 ax.yaxis.set_ticks_position('left')
 
 grid(b=True, which='major', color='grey', linestyle='--')
 
 xlabel('Temperature', fontsize=16, fontweight='bold')
 ylabel('heat capacity per spin', fontsize=16, fontweight='bold')
 plt.title('A plot of heat capacity per spin vs temperature \n for 2x2 system size', fontsize=16, fontweight='bold')
 ylim(0,3)
 
 ttl = ax.title
 ttl.set_position([.5, 1.05])
 
 plot(T2x2_array, hc2x2_array, color="#2E86C1", label="2x2", linewidth=1)
 
 legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0., prop={'size':10})
 
 show()

The python source code for 4x4 plot is shown below:

# heat capacity vs temperature plot for 4x4 system size
# color scheme generated using html color codes from webpage http://htmlcolorcodes.com/
 
 %pylab inline
 import numpy as np
 
 a2x2 = np.loadtxt("4x4_trial_1.dat", delimiter=' ')
 
 # load each data for different system sizes to a new list

T4x4 = a4x4[:,0]
hc4x4 = []
for line in a4x4:
    temperature = line[0]
     energy = line[1]
     energy2 = line[2]
     system_size = 16
     heat_capacity = ((energy2) - (energy)**2)/((temperature**2)*(system_size))
    hc4x4 = hc4x4 + [heat_capacity]
 
 # change list to array
 
 T4x4_array = np.array(T4x4)
 hc4x4_array = np.array(hc4x4)
 
 figure(figsize=(8,5))
 
 font = {'size'   : 16}
 
 # plot using matplotlib
 
 matplotlib.rc('font', **font)
 
 ax = gca()
 ax.spines['right'].set_linewidth(3)
 ax.spines['top'].set_linewidth(3)
 ax.spines['bottom'].set_linewidth(3)
 ax.spines['left'].set_linewidth(3)
 ax.xaxis.set_ticks_position('bottom')
 ax.yaxis.set_ticks_position('left')
 
 grid(b=True, which='major', color='grey', linestyle='--')
 
 xlabel('Temperature', fontsize=16, fontweight='bold')
 ylabel('heat capacity per spin', fontsize=16, fontweight='bold')
 plt.title('A plot of heat capacity per spin vs temperature \n for 4x4 system size', fontsize=16, fontweight='bold')
 ylim(0,3)
 
 ttl = ax.title
 ttl.set_position([.5, 1.05])
 
 plot(T4x4_array, hc4x4_array, color="#138D75", label="4x4", linewidth=1)
 
 legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0., prop={'size':10})
 
 show()

The python source code for 8x8 plot is shown below:

# heat capacity vs temperature plot for 8x8 system size
# color scheme generated using html color codes from webpage http://htmlcolorcodes.com/
 
 %pylab inline
 import numpy as np
 
 a8x8 = np.loadtxt("8x8_trial_1.dat", delimiter=' ')
 
 # load each data for different system sizes to a new list

T8x8 = a8x8[:,0]
hc8x8 = []
for line in a8x8:
    temperature = line[0]
     energy = line[1]
     energy2 = line[2]
     system_size = 64
     heat_capacity = ((energy2) - (energy)**2)/((temperature**2)*(system_size))
    hc8x8 = hc8x8 + [heat_capacity]
 
 # change list to array
 
 T8x8_array = np.array(T8x8)
 hc8x8_array = np.array(hc8x8)
 
 figure(figsize=(8,5))
 
 font = {'size'   : 16}
 
 # plot using matplotlib
 
 matplotlib.rc('font', **font)
 
 ax = gca()
 ax.spines['right'].set_linewidth(3)
 ax.spines['top'].set_linewidth(3)
 ax.spines['bottom'].set_linewidth(3)
 ax.spines['left'].set_linewidth(3)
 ax.xaxis.set_ticks_position('bottom')
 ax.yaxis.set_ticks_position('left')
 
 grid(b=True, which='major', color='grey', linestyle='--')
 
 xlabel('Temperature', fontsize=16, fontweight='bold')
 ylabel('heat capacity per spin', fontsize=16, fontweight='bold')
 plt.title('A plot of heat capacity per spin vs temperature \n for 8x8 system size', fontsize=16, fontweight='bold')
 ylim(0,3)
 
 ttl = ax.title
 ttl.set_position([.5, 1.05])
 
 plot(T8x8_array, hc8x8_array, color="#D68910", label="4x4", linewidth=1)
 
 legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0., prop={'size':10})
 
 show()

The python source code for 16x16 plot is shown below:

# heat capacity vs temperature plot for 16x16 system size
# color scheme generated using html color codes from webpage http://htmlcolorcodes.com/
 
 %pylab inline
 import numpy as np
 
 a16x16 = np.loadtxt("16x16_trial_1.dat", delimiter=' ')
 
 # load each data for different system sizes to a new list

T16x16 = a16x16[:,0]
hc16x16 = []
for line in a16x16:
    temperature = line[0]
     energy = line[1]
     energy2 = line[2]
     system_size = 256
     heat_capacity = ((energy2) - (energy)**2)/((temperature**2)*(system_size))
    hc16x16 = hc16x16 + [heat_capacity]
 
 # change list to array
 
 T16x16_array = np.array(T16x16)
 hc16x16_array = np.array(hc16x16)
 
 figure(figsize=(8,5))
 
 font = {'size'   : 16}
 
 # plot using matplotlib
 
 matplotlib.rc('font', **font)
 
 ax = gca()
 ax.spines['right'].set_linewidth(3)
 ax.spines['top'].set_linewidth(3)
 ax.spines['bottom'].set_linewidth(3)
 ax.spines['left'].set_linewidth(3)
 ax.xaxis.set_ticks_position('bottom')
 ax.yaxis.set_ticks_position('left')
 
 grid(b=True, which='major', color='grey', linestyle='--')
 
 xlabel('Temperature', fontsize=16, fontweight='bold')
 ylabel('heat capacity per spin', fontsize=16, fontweight='bold')
 plt.title('A plot of heat capacity per spin vs temperature \n for 16x16 system size', fontsize=16, fontweight='bold')
 ylim(0,3)
 
 ttl = ax.title
 ttl.set_position([.5, 1.05])
 
 plot(T16x16_array, hc16x16_array, color="#C0392B", label="16x16", linewidth=1)
 
 legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0., prop={'size':10})
 
 show()

The python source code for 32x32 plot is shown below:

# heat capacity vs temperature plot for 32x32 system size
# color scheme generated using html color codes from webpage http://htmlcolorcodes.com/
 
 %pylab inline
 import numpy as np
 
 a32x32 = np.loadtxt("32x32_trial_1.dat", delimiter=' ')
 
 # load each data for different system sizes to a new list

T32x32 = a32x32[:,0]
hc32x32 = []
for line in a32x32:
    temperature = line[0]
     energy = line[1]
     energy2 = line[2]
     system_size = 1024
     heat_capacity = ((energy2) - (energy)**2)/((temperature**2)*(system_size))
    hc32x32 = hc32x32 + [heat_capacity]
 
 # change list to array
 
 T32x32_array = np.array(T32x32)
 hc32x32_array = np.array(hc32x32)
 
 figure(figsize=(8,5))
 
 font = {'size'   : 16}
 
 # plot using matplotlib
 
 matplotlib.rc('font', **font)
 
 ax = gca()
 ax.spines['right'].set_linewidth(3)
 ax.spines['top'].set_linewidth(3)
 ax.spines['bottom'].set_linewidth(3)
 ax.spines['left'].set_linewidth(3)
 ax.xaxis.set_ticks_position('bottom')
 ax.yaxis.set_ticks_position('left')
 
 grid(b=True, which='major', color='grey', linestyle='--')
 
 xlabel('Temperature', fontsize=16, fontweight='bold')
 ylabel('heat capacity per spin', fontsize=16, fontweight='bold')
 plt.title('A plot of heat capacity per spin vs temperature \n for 32x32 system size', fontsize=16, fontweight='bold')
 ylim(0,3)
 
 ttl = ax.title
 ttl.set_position([.5, 1.05])
 
 plot(T32x32_array, hc32x32_array, color="#7D3C98", label="32x32", linewidth=1)
 
 legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0., prop={'size':10})
 
 show()

8. Locating the Curie Temperature

Task 1

Two plots below compares the data obtained from C++ with python for variation in energy per spin and magnetisation per spin with temperature. Both plots below used system size 32x32. For energy vs temperature plots, python and C++ data were very consistent for all lattice sizes and overlapped almost perfectly when plotted on top of each other. For magnetisation, C++ plots showed more clearly defined gradient than the python plots, especially for the larger lattices.


A plot showing energy per spin vs temperature for 32x32 system size comparing data from C++ and python			A plot showing magnetisation per spin vs temperature for 32x32 system size comparing data from C++ and python

The python source code for the energy plot comparing python with C++ data is shown below:

# energy vs temperature plot for 32x32 system sizes
# color scheme generated using html color codes from webpage http://htmlcolorcodes.com/
 
 %pylab inline
 import numpy as np
 
 p32x32 = np.loadtxt("32x32_trial_1.dat", delimiter=' ')
 c32x32 = np.loadtxt("32x32.dat", delimiter=' ')
 
 # load each data for different system sizes to a new list

pT32x32 = p32x32[:,0]
pE32x32 = p32x32[:,1]
newpE32x32 = [x/1024 for x in pE32x32]

cT32x32 = c32x32[:,0]
cE32x32 = c32x32[:,1]
newcE32x32 = cE32x32

# change list to array
 
 pT32x32_array = np.array(pT32x32)
 pE32x32_array = np.array(newpE32x32)
 
 cT32x32_array = np.array(cT32x32)
 cE32x32_array = np.array(newcE32x32)
 
 figure(figsize=(8,5))
 
 font = {'size'   : 16}
 
 # plot using matplotlib
 
 matplotlib.rc('font', **font)
 
 ax = gca()
 ax.spines['right'].set_linewidth(3)
 ax.spines['top'].set_linewidth(3)
 ax.spines['bottom'].set_linewidth(3)
 ax.spines['left'].set_linewidth(3)
 ax.xaxis.set_ticks_position('bottom')
 ax.yaxis.set_ticks_position('left')
 
 grid(b=True, which='major', color='grey', linestyle='--')
 
 xlabel('Temperature', fontsize=16, fontweight='bold')
 ylabel('Energy per spin', fontsize=16, fontweight='bold')
 plt.title('A plot of energy per spin vs temperature \n for 32x32 system sizes', fontsize=16, fontweight='bold')
 ylim(-2.2, -0.2)
 
 ttl = ax.title
 ttl.set_position([.5, 1.05])
 
 plot(pT32x32_array, pE32x32_array, color="#C39BD3", label="python 32x32", linewidth=3)
 plot(cT32x32_array, cE32x32_array, color="#7D3C98", label="C++ 32x32", linewidth=3)
 
 legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0., prop={'size':10})
 
 show()

The python source code for the magnetisation plot comparing python with C++ data is shown below:

# magnetisation vs temperature plot for 32x32 system size
# color scheme generated using html color codes from webpage http://htmlcolorcodes.com/
 
 %pylab inline
 import numpy as np
 
 p32x32 = np.loadtxt("32x32_trial_1.dat", delimiter=' ')
 c32x32 = np.loadtxt("32x32.dat", delimiter=' ')
 
 # load each data for different system sizes to a new list

pT32x32 = p32x32[:,0]
pM32x32 = p32x32[:,3]
newpM32x32 = [x/1024 for x in pM32x32]

cT32x32 = c32x32[:,0]
cM32x32 = c32x32[:,3]
newcM32x32 = cM32x32

# change list to array
 
 pT32x32_array = np.array(pT32x32)
 pM32x32_array = np.array(newpM32x32)
 
 cT32x32_array = np.array(cT32x32)
 cM32x32_array = np.array(newcM32x32)
 
 figure(figsize=(8,5))
 
 font = {'size'   : 16}
 
 # plot using matplotlib
 
 matplotlib.rc('font', **font)
 
 ax = gca()
 ax.spines['right'].set_linewidth(3)
 ax.spines['top'].set_linewidth(3)
 ax.spines['bottom'].set_linewidth(3)
 ax.spines['left'].set_linewidth(3)
 ax.xaxis.set_ticks_position('bottom')
 ax.yaxis.set_ticks_position('left')
 
 grid(b=True, which='major', color='grey', linestyle='--')
 
 xlabel('Temperature', fontsize=16, fontweight='bold')
 ylabel('Magnetisation per spin', fontsize=16, fontweight='bold')
 plt.title('A plot of magnetisation per spin vs temperature \n for 32x32 system sizes', fontsize=16, fontweight='bold')
 ylim(-1.1, 1.1)
 
 ttl = ax.title
 ttl.set_position([.5, 1.05])
 
 plot(pT32x32_array, pM32x32_array, color="#C39BD3", label="python 32x32", linewidth=1)
 plot(cT32x32_array, cM32x32_array, color="#7D3C98", label="C++ 32x32", linewidth=1)
 
 legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0., prop={'size':10})
 
 show()

Task 2 & 3

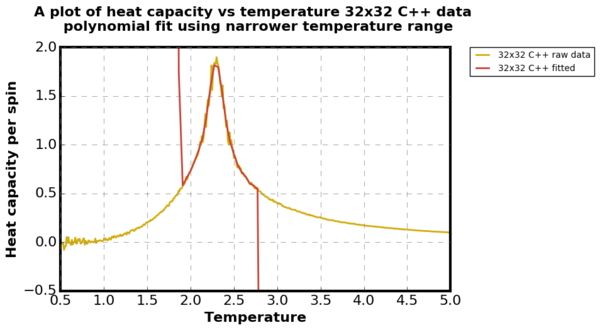
The plot below shows polynomial fit for 32x32 system size using C++ data using the entire temperature range and using a narrower temperature range. Degree of polynomial was used up to 50th order with 1000 spacing between T max and T min for the fit. It was wise to avoid using very high polynomial order as then the fitted function was too similar to the unfitted plot. In this situation, the fitted plot did not have a clear bell shape and hence the maximum of the curve was not clearly defined.


A plot showing heat capacity polynomial fit using entire temperature range for data obtained from C++			A plot showing heat capacity polynomial fit using narrower temperature range for data obtained from C++

The python source code used for the entire temperature range fit for the heat capacity is shown below:

%pylab inline
import numpy as np

data = np.loadtxt("32x32.dat") #assume data is now a 2D array containing two columns, T and C
T = data[:,0] #get the first column
C = data[:,5] # get the second column

#first we fit the polynomial to the data
 fit = np.polyfit(T, C, 50) # fit a third order polynomial
 
 #now we generate interpolated values of the fitted polynomial over the range of our function
T_min = np.min(T)
T_max = np.max(T)
T_range = np.linspace(T_min, T_max, 1000) #generate 1000 evenly spaced points between T_min and T_max
fitted_C_values = np.polyval(fit, T_range) # use the fit object to generate the corresponding values of C

figure(figsize=(8,5))

font = {'size'   : 16}

# plot using matplotlib
 
 matplotlib.rc('font', **font)
 
 ax = gca()
 ax.spines['right'].set_linewidth(3)
 ax.spines['top'].set_linewidth(3)
 ax.spines['bottom'].set_linewidth(3)
 ax.spines['left'].set_linewidth(3)
 ax.xaxis.set_ticks_position('bottom')
 ax.yaxis.set_ticks_position('left')
 
 grid(b=True, which='major', color='grey', linestyle='--')
 
 xlabel('Temperature', fontsize=16, fontweight='bold')
 ylabel('Heat capacity per spin', fontsize=16, fontweight='bold')
 plt.title('A plot of heat capacity vs temperature 32x32 C++ data \n polynomial fit using entire temperature range', fontsize=16, fontweight='bold')
 
 ttl = ax.title
 ttl.set_position([.5, 1.05])
 
 plot(T, C, color="#D4AC0D", label="32x32 C++ raw data", linewidth=2)
 plot(T_range, fitted_C_values, color="#CB4335", label="32x32 C++ fitted", linewidth=2)
 
 legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0., prop={'size':10})
 
 show()

The python source code used for the narrower temperature range fit for the heat capacity is shown below:

%pylab inline
import numpy as np

data = np.loadtxt("32x32.dat") #assume data is now a 2D array containing two columns, T and C
T = data[:,0] #get the first column
C = data[:,5] # get the sixth column

#now we generate interpolated values of the fitted polynomial over the range of our function
T_min = np.min(T)
T_max = np.max(T)

Tmin = 1.9 #for example
Tmax = 2.8 #for example

selection = np.logical_and(T > Tmin, T < Tmax) #choose only those rows where both conditions are true
peak_T_values = T[selection]
peak_C_values = C[selection]

fit = np.polyfit(peak_T_values, peak_C_values, 50) # fit a 100 order polynomial

T_range = np.linspace(T_min, T_max, 100) #generate 1000 evenly spaced points between T_min and T_max
fitted_C_values = np.polyval(fit, T_range) # use the fit object to generate the corresponding values of C

figure(figsize=(8,5))

font = {'size'   : 16}

# plot using matplotlib
 
 matplotlib.rc('font', **font)
 
 ax = gca()
 ax.spines['right'].set_linewidth(3)
 ax.spines['top'].set_linewidth(3)
 ax.spines['bottom'].set_linewidth(3)
 ax.spines['left'].set_linewidth(3)
 ax.xaxis.set_ticks_position('bottom')
 ax.yaxis.set_ticks_position('left')
 ttl = ax.title
 ttl.set_position([.5, 1.05])
 
 grid(b=True, which='major', color='grey', linestyle='--')
 
 ylim(-0.5,2)
 xlabel('Temperature', fontsize=16, fontweight='bold')
 ylabel('Heat capacity per spin', fontsize=16, fontweight='bold')
 plt.title('A plot of heat capacity vs temperature 32x32 C++ data \n polynomial fit using narrower temperature range', fontsize=16, fontweight='bold')
 
 plot(T, C, color="#D4AC0D", label="32x32 C++ raw data", linewidth=2)
 plot(T_range, fitted_C_values, color="#CB4335", label="32x32 C++ fitted", linewidth=2)
 
 legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0., prop={'size':10})
 
 show()

The python source code used to determine the temperature at which the peak heat capacity occurs for the narrower plot above is shown below:

new_T_range = np.linspace(Tmin, Tmax, 1000)
new_fitted_C_values = np.polyval(fit, new_T_range)
Cmax = np.max(new_fitted_C_values)
Tmax = new_T_range[new_fitted_C_values == Cmax]
print(Cmax)
print(Tmax)

JC: Fit looks good and good understanding of polyfit, polyval and loadtxt functions.

Task 4

The variation in the Curie Temperature for different lattice sizes can be modelled by the equation below:

$T_{c, L} = \frac{A}{L} + T_{c, \infty}$

The plot below shows the linear plot of 1/L vs $T_{c, L}$ . The point for 2x2 was ignored as it was anomalous and did not follow the linear trend. Ignoring this point improved the accuracy of Tc for infinite lattice significantly where the literature value was 2.269. Despite the use of small lattice sizes, the obtained y-intercept from the plot below was 2.258 and hence the percentage error was was less than 1% (actual error: 0.48%).


A plot of 1/L vs Tc to determine the Curie Temperature for infinite lattice

JC: Make sure you include a reference in the text for the literature value. Good idea to ignore the 2x2 data.

There were several factors which affected the accuracy of the results. The greatest source of error was due to the fact that only small system sizes were investigated. As mentioned previously, for a small lattice, one spin flip will have a greater impact across the whole system than a larger lattice. Therefore, with more time investigating larger system sizes will more likely to improve the accuracy as they would compensate the poor statistics from the small system sizes. Furthermore, the original paper by Onsager stated that the maximum heat capacity will not occur precisely at the asymptotic critical temperature for the finite crystals. Hence, despite the good accuracy, a precise calculation of Tc is impossible with a finite model. In the literature it was stated that incorporating finite size scaling to this model can improve the accuracy further ^[5]. Finally, increasing the number of Monte Carlo steps in the simulation would lead to higher quality data. Greater time step would lead to greater number of samples collected around the states the system is most likely to occupy leading to better distribution.

The python source code used to determine the Curie Temperature for the infinite lattice is shown below:

%pylab inline
import numpy as np

data = np.loadtxt("curie_temp.txt") 
L = data[:,0] #get the first column
Tc = data[:,1] # get the second column
rev_L = []

for i in L:
    rev_L = rev_L + [1/i]
 
 new_L = rev_L[1:]
 new_Tc = Tc[1:]
 
 #first we fit the polynomial to the data
 fit = np.polyfit((new_L), new_Tc, 1) # fit a first order polynomial
 
 #now we generate interpolated values of the fitted polynomial over the range of our function
L_min = np.min(new_L)
L_max = np.max(new_L)
L_range = np.linspace(L_min, L_max, 1000) #generate 1000 evenly spaced points between T_min and T_max
fitted_Tc_values = np.polyval(fit, L_range) # use the fit object to generate the corresponding values of C

figure(figsize=(8,5))

font = {'size'   : 16}

# plot using matplotlib
 
 matplotlib.rc('font', **font)
 
 ax = gca()
 ax.spines['right'].set_linewidth(3)
 ax.spines['top'].set_linewidth(3)
 ax.spines['bottom'].set_linewidth(3)
 ax.spines['left'].set_linewidth(3)
 ax.xaxis.set_ticks_position('bottom')
 ax.yaxis.set_ticks_position('left')
 ttl = ax.title
 ttl.set_position([.5, 1.05])
 ylim(2.2, 2.6)
 
 grid(b=True, which='major', color='grey', linestyle='--')
 
 xlabel('1/lattice size', fontsize=16, fontweight='bold')
 ylabel('Temperature', fontsize=16, fontweight='bold')
 plt.title('A plot of heat capacity per spin vs temperature for C++ data \n 32x32 system size with narrower fitting range', fontsize=16, fontweight='bold')
 
 plot(L_range, fitted_Tc_values, color="#2980B9", label="32x32 C++ fitted", linewidth=2)
 scatter(rev_L, Tc, color="#17A589", label="original data", linewidth=3)
 
 legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0., prop={'size':10})
 
 show()

9. Extension

As noted in the original paper by Onsager, the study by Kramers and Wannier ^[6] showed that the maximum heat capacity is expected to increase linearly with log(n) where n is the width of the 2D lattice. An extension plot was carried out to check whether the data collected for this report was consistent with this result. The figure below outlines the variation in heat capacity with log(L) for the C++ data. A clear linear trend was observed, consistent with the expectations.


A plot of Cv vs log(L) illustrating the linear relation between heat capacity and log of lattice width

JC: Nice idea to extend the investigation. The data points look like they fit to a curve, was there any evidence for this in the original paper?

The code used to generate the plot above is shown below:

%pylab inline
import numpy as np

data = np.loadtxt("curie_temp.txt") 
L = data[:,0] #get the first column
Tc = data[:,1] # get the second column
Cv = data[:,2]
log_L = []

for i in range(len(L)):
    log_L = log_L + [log10(L[i])]
 
 fit = np.polyfit(log_L, Cv, 1) # fit a first order polynomial
 
 L_min = np.min(log_L)
 L_max = np.max(log_L)
 L_range = np.linspace(L_min, L_max, 1000) #generate 1000 evenly spaced points between L_min and L_max
 fitted_Cv_values = np.polyval(fit, L_range) # use the fit object to generate the corresponding values of C
 
 figure(figsize=(8,5))
 
 font = {'size'   : 16}
 
 # plot using matplotlib
 
 matplotlib.rc('font', **font)
 
 ax = gca()
 ax.spines['right'].set_linewidth(3)
 ax.spines['top'].set_linewidth(3)
 ax.spines['bottom'].set_linewidth(3)
 ax.spines['left'].set_linewidth(3)
 ax.xaxis.set_ticks_position('bottom')
 ax.yaxis.set_ticks_position('left')
 ttl = ax.title
 ttl.set_position([.5, 1.05])
 
 grid(b=True, which='major', color='grey', linestyle='--')
 
 xlabel('log10(L)', fontsize=16, fontweight='bold')
 ylabel('Cv', fontsize=16, fontweight='bold')
 plt.title('A plot of heat capacity per spin vs log10(L) for C++ data', fontsize=16, fontweight='bold')
 
 plot(L_range, fitted_Cv_values, color="#2980B9", label="fitted", linewidth=2)
 scatter(log_L, Cv, color="#17A589", label="original data", linewidth=3)
 
 legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0., prop={'size':10})
 
 show()
 
 print(fit)

↑ K.A. Dill, S. Bromberg, Molecular Driving Forces , Garland Science, New York, 2nd Ed., pp. 12, 2002
↑ P. Atkins, J. de Paula, "Physical Chemistry", Oxford University Press, Oxford, 8th Ed., pp. 129-130, 2006
↑ W. Karuth, Statistical Mechanics: Algorithms and Computations", Oxford University Press, Oxford, pp. 234-235, 2006
↑ L. Onsager, APS Physics, 1944, 65, 117-149, DOI: https://doi.org/10.1103/PhysRev.65.117
↑ T. Preis, P. Virnau, W. Paul, J.J. Schneider, Elsevier Journal of Computational Physics, 2009, 228, 4468-4477
↑ H.A. Kramers, G.H. Wannier, APS Physics, 1941, 60, 263-276, DOI:https://doi.org/10.1103/PhysRev.60.263

[Driving_Forces-1] K.A. Dill, S. Bromberg, Molecular Driving Forces , Garland Science, New York, 2nd Ed., pp. 12, 2002

[Atkins-2] P. Atkins, J. de Paula, "Physical Chemistry", Oxford University Press, Oxford, 8th Ed., pp. 129-130, 2006

[Statistics-3] W. Karuth, Statistical Mechanics: Algorithms and Computations", Oxford University Press, Oxford, pp. 234-235, 2006

[Onsager-4] L. Onsager, APS Physics, 1944, 65, 117-149, DOI: https://doi.org/10.1103/PhysRev.65.117

[Preis-5] T. Preis, P. Virnau, W. Paul, J.J. Schneider, Elsevier Journal of Computational Physics, 2009, 228, 4468-4477

[Kramers-6] H.A. Kramers, G.H. Wannier, APS Physics, 1941, 60, 263-276, DOI:https://doi.org/10.1103/PhysRev.60.263

[1]

[2]

[3]

[4]

[5]

[6]