Talk:Mod:run simulation run

JC: General comments: This is a very good report, well done. You have carried out all of the tasks very carefully and paid special attention to units and the sources of errors.

Simulation of a simple liquid

Using molecular dynamics, several key physical properties can be calculated under different conditions. For the chosen system, a timestep no larger than 0.0025 u_T* should to be used for accurate results. The density of a gas decreases with increasing pressure and decreasing temperature and is much lower than that predicted by the ideal gas law. Also, heat capacity is not constant but decreases with temperature and increases with pressure. Computing the radial distribution function shows that gases have a preferred interatomic separation but no medium or long range ordering while liquids form shells of atoms. For a solid, there is long range ordering (regular lattice) who's lattice constant can be predicted very well from the RDF. An atom in a face centered cubic lattice has 12 nearest neighbors. Finally, the well known fact that diffusion is fastest in a gas, slower in a liquid and non existent in a crystal can be confirmed. There is a strong pressure dependence for a gas.

Figure 1:Liquid modeled balls n.b. This is a gif but the resolution is too high to be displayd in the main body

Units

Throughout this report arbitrary units will be used since non of the values are empirical. For example, u_r is the unit for r (distance) or u_ρ (density). An asterisk denotes that this is a unit for the reduced quantity e.g. u_r^*. The reduced unit may be converted into the corresponging real unit the same way that the reduced quanitity may be converted into the real quantity i.e. $u_r^{*}=u_r\times \sigma$.

Introduction to molecular dynamics simulation

Velocity Verlet Algorithm

Task

TASK Open the file HO.xls. In it, the velocity-Verlet algorithm is used to model the behaviour of a classical harmonic oscillator. Complete the three columns "ANALYTICAL", "ERROR", and "ENERGY": "ANALYTICAL" should contain the value of the classical solution for the position at time $t$, "ERROR" should contain the absolute difference between "ANALYTICAL" and the velocity-Verlet solution (i.e. ERROR should always be positive -- make sure you leave the half step rows blank!), and "ENERGY" should contain the total energy of the oscillator for the velocity-Verlet solution. Remember that the position of a classical harmonic oscillator is given by $x\left(t\right)=A\cos (\omega t+\varphi )$ (the values of $A$, $\omega$, and $\varphi$ are worked out for you in the sheet).

Analytical is the position of the classical harmonic oscillator as a function of x (see fig. 2a) and given by:

$x\left(t\right)=A\cos (\omega t+\varphi )$

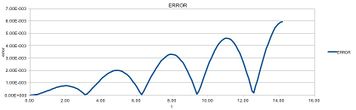
The absolute error between analytical and velocity Verlet (see fig. 2b) is given by:

$Error(t)=\mid x_{v.verlet}(t)-x_{analytical}(t)\mid$

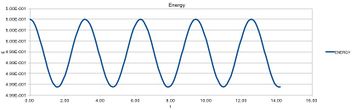
The total energy of the harmonic oscillator (see fig. 2c) is made up of kinetic and potential energy contributions and hence given by:

$E_{total}=E_P+E_K=\frac{1}{2}k{x}^2+\frac{1}{2}{m}^{*}{v}^2$

where E_P = potential energy
        E_K = kinetic energy
        k = spring constant, given by:   $k=\frac{{\omega }^2}{m^{*}}$
        m* = effective (=reduced) mass
        v = velocity

Results:

Figure 2a Position as function of time: The position oscillates arond a mean value. Note how analytical and velocity verlet appear indistinguishable on the graph.

Figure 2b Error as function of time: Note the fluctuating, increasing nature.

Figure 2c Energy as function of time:It oscillates.

As expected, the position of the atoms oscillates around a mean value using the equation for the harmonic oscillator. It can be seen that the velocity verlet algorithm and equatin for harmonic show very similar, but not identical results. This can be seen more clearly by examining error as a function of time (fig. 2b). It is also noteworthy that the error is not constant and resembles the square of a sine wave with increasing amplitude.

The energy of the system oscillates, disobeying the law of conservation of energy, indicating an imperfection in the mathematicl methods.

JC: Why does the error have this shape?

Task
For the default timestep value, 0.1, estimate the positions of the maxima in the ERROR column as a function of time. Make a plot showing these values as a function of time, and fit an appropriate function to the data.

Figure 3: Error peaks against time:a linear relationship can be seen due to accumulation of error.

The dependence of maximum error and time is linearly increasing with a slope of 0.0004 ur* uT*-1 and an intercept of 7 * 10-7 ur*, see figure 3.

Every calculation has some small error and, since every calculation is based on the calculation before, the errors add up becoming larger as the simulation goes on. The error is periodic with the "amplitude" of the function increasing. The error is largest where the function is 0 and smallest (almost 0) where the function has a maximum or minimum.

Task
Experiment with different values of the timestep. What sort of a timestep do you need to use to ensure that the total energy does not change by more than 1% over the course of your "simulation"? Why do you think it is important to monitor the total energy of a physical system when modelling its behaviour numerically?

Figure 4: Maximum energy fluctuation as a function of timestep: A non linear increase can be seen.

Since only the harmonic oscillator is modeled and no other particles (essentially an isolated system) the total energy of the harmonic oscillator is the total energy of the system and hence has to remain constant to conserve energy. The energy is constantly being converted between kinetic and potential energy (they fluctuate) but the sum of both needs to remain constant to describe the system over time. This will never be the case due to computational limits however, one can try to keep the fluctuation as small as possible. Testing different time steps between 0.01 u_T^* and 1.6 u_T^* shows two trends: Firstly, the smaller the timestep, the smaller the difference between global minimum and global maximum. This means the system can be modeled more accurately if the timestep is reduced. However, decreasing the timestep means increasing the number of steps (i.e. calculations) in the simulation by the same factor and hence more computational power is required. Secondly, this dependence is exponential (see fig. 4). This means that at some point decreasing the timestep will not result in a major gain in accuracy and may not be worth it anymore. For a timestep of 0.2 u_T^* the energy change (difference between global maximum and minimum) is 1% of the global maximum. For a timestep of 0.1 u_T^* (twice the computational power required) the resulting change in energy is 0.25 %, i.e. not much smaller.

JC: Nice, methodical analysis and good choice of timestep.

Atomic Forces

Task

For a single Lennard-Jones interaction, $\varphi \left(r\right)=4ϵ(\frac{{\sigma }^{12}}{r^{12}}-\frac{{\sigma }^6}{r^6})$, find the separation, $r_0$, at which the potential energy is zero. What is the force at this separation? Find the equilibrium separation, $r_{eq}$, and work out the well depth ($\varphi \left(r_{eq}\right)$). Evaluate the integrals $\underset{2\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)\mathrm{d}r$, $\underset{2.5\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)\mathrm{d}r$, and $\underset{3\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)\mathrm{d}r$ when $\sigma =ϵ=1.0$

Finding r₀:

$\varphi \left(r\right)=4ϵ(\frac{{\sigma }^{12}}{r_0^{12}}-\frac{{\sigma }^6}{r_0^6})=0$

$\frac{{\sigma }^{12}}{r_0^{12}}=\frac{{\sigma }^6}{r_0^6}$

$\frac{\sigma }{r_0}=1$

$r_0=\pm \sigma$

Obviously, a negative bond distance is not possible, hence there is only one solution:

$r_0=\sigma$

Force is given by the derivative of energy/potential with respect to distance hence:

$F(r)=-\frac{\partial \varphi (r)}{\partial r}=\frac{\partial }{\partial r}4ϵ(\frac{{\sigma }^{12}}{r_0^{12}}-\frac{{\sigma }^6}{r^6})$

$F(r)=24ϵ(\frac{2{\sigma }^{12}}{r^{13}}-\frac{{\sigma }^6}{r^7})$

$F(r_0)=24ϵ(\frac{2{\sigma }^{12}}{{\sigma }^{13}}-\frac{{\sigma }^6}{{\sigma }^7})=24ϵ(\frac{2}{\sigma }-\frac{1}{\sigma })$

$F(r_0)=24\frac{ϵ}{\sigma }$

Finding r_eq:

At the equilibrium bond distance there is no force acting on the bond hence r_eq can be found by setting the first derivative zero.

$F(r_{eq})=-\frac{\partial \varphi (r_{eq})}{\partial r}=0$

$24ϵ(\frac{2{\sigma }^{12}}{r_{eq}^{13}}-\frac{{\sigma }^6}{r_{eq}^7})=0$

$\frac{2{\sigma }^{12}}{r_{eq}^{13}}=\frac{{\sigma }^6}{r_{eq}^7}$

$r_{eq}=\sqrt[6]{2}\sigma$

Note that since the shape of the Lennard Jones potential is well known and doesn't have a maximum or saddle point, it is not necessary to check the second derivative to confirm that this point is a minimum.

The well depth at this position is:

$\varphi \left(r_{eq}\right)=4ϵ(\frac{{\sigma }^{12}}{r^{12}}-\frac{{\sigma }^6}{r^6})$

$\varphi \left(r_{eq}\right)=4ϵ(\frac{{\sigma }^{12}}{(2^{\frac{1}{6}}\sigma {)}^{12}}-\frac{{\sigma }^6}{(2^{\frac{1}{6}}\sigma {)}^6})$

$\varphi \left(r_{eq}\right)=-ϵ$

Integrals: The indefinite integral as general solution is:

$\int \varphi (r)dr=\int 4ϵ(\frac{{\sigma }^{12}}{r^{12}}-\frac{{\sigma }^6}{r^6})dr$

$\int \varphi (r)dr=4ϵ(\frac{{\sigma }^6}{5r^5}-\frac{{\sigma }^{12}}{11r^{11}})+C$

Applying limits and considering that:

$\underset{r\to \mathrm{\infty }}{\lim }(\frac{{\sigma }^6}{5r^5}-\frac{{\sigma }^{12}}{11r^{11}})=0$

and

$ϵ=\sigma =1$

$\underset{2\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi (r)dr=4ϵ(\frac{{\sigma }^6}{5r^5}-\frac{{\sigma }^{12}}{11r^{11}}){|}_{2\sigma }^{\mathrm{\infty }}$

$\underset{2\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi (r)dr=-(\frac{1}{5*2^5}-\frac{1}{11*2^{11}})$

$\underset{2\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi (r)dr=-2.48*10^{-2}{u}_{\mathrm{r}}^{\mathrm{2}}$

Similarly:

$\underset{2.5\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi (r)dr=-8.17*10^{-3}{u}_{\mathrm{r}}^{\mathrm{2}}$

$\underset{3\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi (r)dr=-3.29*10^{-3}{u}_{\mathrm{r}}^{\mathrm{2}}$

The calculated areas are the areas that would be "lost" or ignored in the calculation if the cutoff was performed at 2, 2.5 and 3 σ, respectively. It can be seen that the area between 3 σ and infinity is very small, especially compared to that between 2 and infinity, hence it may be safe to ignore those in order to save computational complexity, while not sacrificing too much accuracy.

JC: All maths correct and well presented.

Periodic Boundary Conditions

Task
Estimate the number of water molecules in 1ml of water under standard conditions. Estimate the volume of $10000$ water molecules under standard conditions.

Assuming standard conditions of T = 25 °C and P = 1 atm:

$1\mathrm{m}\mathrm{o}\mathrm{l}{\mathrm{H}}_{\mathrm{2}}\mathrm{O}...............18.02\mathrm{m}\mathrm{L}$

$1\mathrm{m}\mathrm{L}...............0.055\mathrm{m}\mathrm{o}\mathrm{l}$

$0.055\mathrm{m}\mathrm{o}\mathrm{l}...............3.34*10^{22}\mathrm{m}\mathrm{o}\mathrm{l}\mathrm{e}\mathrm{c}\mathrm{u}\mathrm{l}\mathrm{e}\mathrm{s}$

Hence, there are 3.34 * 10²² molecules in one milliliter of water.

$1\mathrm{m}\mathrm{L}...............3.34*10^{22}\mathrm{m}\mathrm{o}\mathrm{l}\mathrm{e}\mathrm{c}\mathrm{u}\mathrm{l}\mathrm{e}\mathrm{s}$

$1\mathrm{m}\mathrm{o}\mathrm{l}\mathrm{e}\mathrm{c}\mathrm{u}\mathrm{l}\mathrm{e}...............2.99*10^{-23}\mathrm{m}\mathrm{L}$

$10^4\mathrm{m}\mathrm{o}\mathrm{l}\mathrm{e}\mathrm{c}\mathrm{u}\mathrm{l}\mathrm{e}\mathrm{s}...............2.99*10^{-19}\mathrm{m}\mathrm{L}$

Hence 10,000 molecules occupy a volume of 2.99 * 10^-19 mL.

Task
Consider an atom at position $(0.5,0.5,0.5)$ in a cubic simulation box which runs from $(0,0,0)$ to $(1,1,1)$. In a single timestep, it moves along the vector $(0.7,0.6,0.2)$. At what point does it end up, after the periodic boundary conditions have been applied?

The position vectors are added up and periodic boundary conditions are applied by subtracting any value larger than the box length (here 1 in all 3 dimensions) by the box length:

$\left(\begin{array}{c}0.5\\ 0.5\\ 0.5\\ \end{array}\right)+\left(\begin{array}{c}0.7\\ 0.6\\ 0.2\\ \end{array}\right)=\left(\begin{array}{c}1.2\\ 1.1\\ 0.7\\ \end{array}\right)\equiv \left(\begin{array}{c}0.2\\ 0.1\\ 0.7\\ \end{array}\right)$

The final position is (0.2, 0.1, 0.7).

Reduced Units

Task
The Lennard-Jones parameters for argon are $$\begin{gathered} \sigma =0.34\mathrm{n}\mathrm{m},ϵ \\ / \\ {k}_B=120\mathrm{K} \end{gathered}$$. If the LJ cutoff is $r^{*}=3.2$, what is it in real units? What is the well depth in $$\begin{gathered} {\mathrm{k}\mathrm{J} \\ \mathrm{m}\mathrm{o}\mathrm{l}}^{-1} \end{gathered}$$? What is the reduced temperature $T^{*}=1.5$ in real units?

$r=r^{*}\sigma =1.08\mathrm{n}\mathrm{m}$

$$\begin{gathered} \varphi (r_{eq})=-ϵ=-120*k_B=1.656*10^{-21}\mathrm{J}=-0.997{\mathrm{k}\mathrm{J} \\ \mathrm{m}\mathrm{o}\mathrm{l}}^{-1} \end{gathered}$$

$T=T^{*}\frac{ϵ}{k_B}=180\mathrm{K}$

JC: All calculations correct.

Equilibration

Creating the simulation box

Task
Why do you think giving atoms random starting coordinates causes problems in simulations? Hint: what happens if two atoms happen to be generated close together?

First, atoms have to be created at (almost) random positions. The first steps in the calculation will then rearrange these atoms to form an equilibrium state, which can then be measured. Placing the atoms copletly randomly has two main issues: atoms being on the same spot and atoms being very close to each oter. The former could be solved easily by telling the program that the same spacial positon cannot be taken up twice (take it out of the infinite "pool" of positions). The latter is a bigger issiue that cannot be overcome as easily. As the interatomic separation approaches zero the potential approaches infinity. A simulation where two atoms are very close to each other would be unrealistic as the repulsion would be incredibly high. Therefore, one has to start the simulation in a state where neither are possible such as a regular lattice, which is then melted.

JC: A configuration with overlapping atoms and high repulsion will be unstable and will require a much smaller timestep to prevent the simulation from crashing.

Task
Satisfy yourself that this lattice spacing corresponds to a number density of lattice points of $0.8$. Consider instead a face-centred cubic lattice with a lattice point number density of 1.2. What is the side length of the cubic unit cell?'

A cubic lattice with spacing of 1.07722 u_r^* is created. The volume of the box is therefore $1.07722^3{u}_{{\mathrm{r}}^{\mathrm{*}}}^{\mathrm{3}}$. There is lattice point per simple cubic unit cell hence the denisty is

$\frac{N}{V}=\frac{N}{a^3}=\frac{1}{1.07722^3}=0.8\frac{latticepoints}{u_{r^{*}}^3}$

Rearranging the equation and keeping in mind that the FCC unit cell has 4 lattice points:

$a=\sqrt[3]{N(\frac{N}{V}{)}^{-1}}=\sqrt[3]{4\frac{1}{1.2}}=1.49{\mathrm{u}}_{{\mathrm{r}}^{\mathrm{*}}}$

Task
Consider again the face-centred cubic lattice from the previous task. How many atoms would be created by the create_atoms command if you had defined that lattice instead?

1000 unit cells are created. Had the create_atoms command used fcc instead if sc, 4000 atoms would have been created.

JC: Correct.

Setting the properties of the atoms

Task
Using the LAMMPS manual, find the purpose of the following commands in the input script: mass 1 1.0 pair_style lj/cut 3.0 pair_coeff * * 1.0 1.0

 mass 1 1.0 

defines the mass: The first number is the atom type who's mass is being defined (only one type here, if there were more types this command would have to be repeated for each atom type). The second number is the mass of that atom type, which is 1.0 u_m^* in this case.

 pair_style lj/cut 3.0 

defines the cutoff of pairwise interactions between two particles: "lj/cut" defines the type of interaction: the Lennard Jones potential. The LJ cutoff is 3 u_r^* i.e. 3 σu_r. In the previous section it was seen that this cutoff only cuts off very little interactions and will yield accurate results.

 pair_coeff * * 1.0 1.0  

defines the pairwise force field coefficients: the first two values (* and *, here) define to which particles the definition applies. e.g. 1 2 would meen between atoms 1 and 2. The asterisk means all types. The last two values (1.0 and 1.0, here) are the coefficients.

JC: What are the coefficients in this case (considering you are using a Lennard-Jones potential)?

Task
Given that we are specifying ${\mathbf{x}}_i\left(0\right)$ and ${\mathbf{v}}_i\left(0\right)$, which integration algorithm are we going to use?

The velocity verlet algorithm is used: both position and velocity at time 0 are defined and their behavior as a function of time is modeled.

JC: Why can't the standard Verlet algorithm be used in this case?

Running the simulation

Task

Look at the lines below. ### SPECIFY TIMESTEP ### variable timestep equal 0.001 variable n_steps equal floor(100/${timestep}) variable n_steps equal floor(100/0.001) timestep ${timestep} timestep 0.001 ### RUN SIMULATION ### run ${n_steps} run 100000 The second line (starting "variable timestep...") tells LAMMPS that if it encounters the text ${timestep} on a subsequent line, it should replace it by the value given. In this case, the value ${timestep} is always replaced by 0.001. In light of this, what do you think the purpose of these lines is? Why not just write: timestep 0.001 run 100000

This makes it easier to change the timestep. Otherwise one would have to go through the entire script and change it every time it appears to change the timestep. This may not be much more effort here but in a larger script it is always a big help to define variables only once, preferably in a well visible position.

Visualising the trajectory

Figure 5: Liquid modelled as points with two atoms as balls (the gif cannot be displayd in the body because the resolution is too high, it is necessary to open it)

It can be seen that the liquid starts off as a regular lattice as defined by the script and rearranges quickly into a more realistic liquid (see fig. 1 and 5). After a few timesteps the liquid looks completely disordered with no resemblence to the simple cubic lattice it started off as. This can be seen better when only two atoms are treated as balls and all others as points. The balls sometimes jump from one edge to another, showing the periodic boundary conditions.

Checking equilibration

Task

make plots of the energy, temperature, and pressure, against time for the 0.001 timestep experiment (attach a picture to your report). Does the simulation reach equilibrium? How long does this take? When you have done this, make a single plot which shows the energy versus time for all of the timesteps (again, attach a picture to your report). Choosing a timestep is a balancing act: the shorter the timestep, the more accurately the results of your simulation will reflect the physical reality; short timesteps, however, mean that the same number of simulation steps cover a shorter amount of actual time, and this is very unhelpful if the process you want to study requires observation over a long time. Of the five timesteps that you used, which is the largest to give acceptable results? Which one of the five is a particularly bad choice? Why?

Figure 6: Energy, pressure and temperature against time for a timestep of 0.001 note that the magnitude of the fluctuations is very small compared to the mean for energy. This is larger for temperature and pressure. Note also that the first fluctuation is very large for all measurements (about the same dimensions as the y axis).

Figure 7: Energy against time for different timesteps

For dt = 0.001 u_t^* temperature, energy and pressure reach equilibrium after a very short time, after which they fluctuate around a mean value (see fig. 6).

The simulatins use the NVE ensemble, meaning that all other thermodynamic properties are allowed to fluctuate, as can be seen for temperature and pressure.

Energy, however, should not be allowed to fluctuate, even though it clearly does.This is beacuse even though energy was "fixed", the program cannot actually fix the energy entirely. The same is true for temperature in the NVT enemble. It was proposed that applying a thermostat (measuring the temperatrue and readjusting it accordingly) can constrict the temperature to be very close to the defined temperature (as is done in later simulations). It may be possible to apply something similar to this system so that energy is measured and readjusted after every timestep. While this may decrease the extent of the fluctuations (σ(E)) it will not have a signifficant effect on the mean energy. It is also noteworthy that energy fluctuates much less than temperature or pressure compared to the mean, indicating that the program makes a good effort at keeping it constant.

The energy for timesteps 0.001 u_t^*, 0.0025 u_t^*, 0.0075 u_t^* and 0.01 u_t^* reaches a mean equilibrium value very soon while the energy using timestep 0.015 u_t^* doesn't (see fig. 7). Therefore 0.015 u_t^* is clearly too large to be used. Fluctuations around the mean value decrease with decreasing timestep. While 0.01 u_t^* and 0.0075 u_t^* reach equilibrium and have a very small standard deviation, their final mean energies are significantly higher than those of 0.0025 u_t^* and 0.001 u_t^*. It is not uncommon for computational simulations to yield a mean higher energy than the real energy, which will lie just below the lowest computed result. Therefore, 0.0025 u_t^* was chosen as compromise between accuracy and computational cost. See table 1 for mean energy and standard deviation.

JC: Energy should not depend on the choice of timestep. The lowest two timesteps have the same average energy which makes them better choices than the higher timesteps which have a higher average energy.

Timestep /ut*	Mean /uE*	STDEV /uE*	Comment
0.001	-3.1842	0.0007	Accurate and precise
0.0025	-3.1838	0.0004	Accurate and precise
0.0075	-3.1823	0.0005	Inaccurate but precise
0.01	-3.1813	0.0007	Inaccurate but precise
0.015	-3.1495	0.0029	Inaccurate and imprecise

      Table 1: mean energy and standard deviation for the different timesteps.

These values were calculated from the last 200 measurements only. There is a compromise to be made here again: the fewer values the less precise the mean, however, later values will be more accurate than early values as the system will be closer to equilibrium then. Averaging over the last 100 data points doesn't change the result for dt = 0.001 u_t^*. For 0.0025 u_t^* the energy is different by 0.0001 u_t^* for and even more different for larger timesteps, indicating that the mean still changes slightly for higher timesteps even though the graph looks like it doesn't. There was no visible trend (for some, the means over 100 were slightly higher than those over 200 for others slighly lower) and this change may only be error. The smallest timestep seems to have a larger standard deviation than the next largest two, however that is most likely insignificant as the difference is so small that it may just be a coincidence. The only significant difference in standard deviation is that between the largest timestep and all others.

Running simulations under specific conditions

Temperature and Pressure Control

Task

Choose 5 temperatures (above the critical temperature $T^{*}=1.5$), and two pressures (you can get a good idea of what a reasonable pressure is in Lennard-Jones units by looking at the average pressure of your simulations from the last section). This gives ten phase points — five temperatures at each pressure. Create 10 copies of npt.in, and modify each to run a simulation at one of your chosen $(p,T)$ points. You should be able to use the results of the previous section to choose a timestep. Submit these ten jobs to the HPC portal. While you wait for them to finish, you should read the next section.

The following conditions were chosen: timestep = 0.0025 u_t^*, p* = 2.0 and 3.0 u_p^*, T* = 1.5, 2.0, 2.5, 3.0, 3.5 u_T^*

Thermostats and Barostats

Task
We need to choose $\gamma$ so that the temperature is correct $T=\mathfrak{𝔗}$ if we multiply every velocity $\gamma$. We can write two equations: $\frac{1}{2}\sum _i{m}_i{v}_i^2=\frac{3}{2}N{k}_{B}T$ $\frac{1}{2}\sum _i{m}_i{\left(\gamma v_i\right)}^2=\frac{3}{2}N{k}_B\mathfrak{𝔗}$ Solve these to determine $\gamma$

Dividing one equation by the other:

$\frac{\frac{1}{2}\sum _i{m}_i{v}_i^2}{\frac{1}{2}\sum _i{m}_i{\left(\gamma v_i\right)}^2}=\frac{\frac{3}{2}N{k}_{B}T}{\frac{3}{2}N{k}_B\mathfrak{𝔗}}$

Canceling out as much as possible

$\frac{\sum _i{m}_i{v}_i^2}{\sum _i{m}_i{\left(\gamma v_i\right)}^2}=\frac{T}{\mathfrak{𝔗}}$

γ is a constant and can be taken out of the sumation

$\frac{1}{{\gamma }^2}\frac{\sum _i{m}_i{v}_i^2}{\sum _i{m}_i{v}_i^2}=\frac{T}{\mathfrak{𝔗}}$

Now the summation can be canceled out too, so that:

$\gamma =\sqrt{\frac{\mathfrak{𝔗}}{T}}$

JC: Good, clear derivation.

Examining the Input Script

Task
Use the manual page to find out the importance of the three numbers 100 1000 100000. How often will values of the temperature, etc., be sampled for the average? How many measurements contribute to the average? Looking to the following line, how much time will you simulate?

The first number defines how often values will be aquired, i.e. every 100 timesteps. The second number specifies the number of values used to calculate the average will be taken, i.e. 1000. The final nunber speifies the number of timesteps carried out. 100 averages are taken, each over 1000 values hence 100,000 timesteps are needed.

Plotting the Equations of State

Task

When your simulations have finished, download the log files as before. At the end of the log file, LAMMPS will output the values and errors for the pressure, temperature, and density $\left(\frac{N}{V}\right)$. Use software of your choice to plot the density as a function of temperature for both of the pressures that you simulated. Your graph(s) should include error bars in both the x and y directions. You should also include a line corresponding to the density predicted by the ideal gas law at that pressure. Is your simulated density lower or higher? Justify this. Does the discrepancy increase or decrease with pressure?

Figure 8: Density against temperature for 2 different reduced pressures using velocity verlet and ideal gas law. Note that the points are connected with thin dotted lines to make the downwards trend more visible, these are not trendlines or predictions of intermediate points. Note also that it may be necessary to view the picture in full resolution to see y error bars

It can be seen that, as expected increasing temperature as well as decreasing pressure decreases the density (see fig.8). It can also be seen that the ideal gas law (N/V = P/T*) predicts a much higher density than molecular dynamics. This is because molecular dynamics uses the energy surface of the Lennard-Jones potential which considers interparticle interactions. The ideal gas law assumes no such interaction and hence ignores the high repulsion as particles get very close to each other. The discrepancy is largest for low temperatures and high pressures since that's where interatomic interactions are strongest.

Heat Capacity Calculation

Task

As in the last section, you need to run simulations at ten phase points. In this section, we will be in density-temperature $({\rho }^{*},T^{*})$ phase space, rather than pressure-temperature phase space. The two densities required at $0.2$ and $0.8$, and the temperature range is $2.0,2.2,2.4,2.6,2.8$. Plot $C_V/V$ as a function of temperature, where $V$ is the volume of the simulation cell, for both of your densities (on the same graph). Is the trend the one you would expect? Attach an example of one of your input scripts to your report.

Heat capacity can be calculated from fluctuations in energy at constant temperature.The input files from the previous section were modified so that they can be used to calculate heat capacities. Two major changes needed to be made: Firstly, changing ensemble from NPE to NVT (this section seeks to examine energy at constant temperature hence energy has to be unfixed and temperature fixed). The previously described thermostat is used too. Secondly, energy and temperature need to be measured by the system, hence the aves command needs to be modified to include these. The number of atoms is measured too although this is constant and one could simply calculate the number of atoms from the input file or read them off the log file (however, it's easiest to make the program do it). Finally, rather than manually calculating the heat capacity in the analysis, the program can be told to do that too.

An example of the input script can be found here: File:Mod-run simulation run d02t2.in

A few lines to point out:

fix aves all ave/time 100 1000 100000 v_dens v_temp v_etotal v_etotal2 v_atoms 

Measures 100 averages over 1000 measuremnts each (hence 100,000 runs) and calculates average density (first argument), average temperature (second argument), average total energy (3^rd), average of the squared total energy (4^th) and number of atoms (5^th).

Note that average total energy squared i.e. <E²> is not the same as the square of the average total energy <E>² as the former is computed by first squaring, then averaging whereas the latter is computed by first averaging then squaring. Hence the need to define and measure etotal2 separately. The difference between <E²> <E>² gives the fluctuation in energy, which is proportional to heat capacity.

variable cv equal (f_aves[5]^2)*(f_aves[4]-f_aves[3]^2)/(f_aves[2]^2)

Figure 9 Heat capacity agsinst temperature for two different densities Note that low lattice spacing (0.2, blue line) corresponds to high density/pressure.

Is the equation for heat capacity, just written in code:

$C_V=N^2\frac{⟨E^2⟩-{⟨E⟩}^2}{T^{*2}}$

Where
    f_aves[5] = N (the 5^th argument, i.e. number of atoms)
   f_aves[4] = <E²> (4^th argument)
   f_aves[3] = <E>² (3^rd argument)
   f_aves[2] = T*: reduced temperature, (2^nd argument)

Note that the program uses reduced temperature (k_BT) but heat capacity is

$C_V=\frac{⟨E^2⟩-{⟨E⟩}^2}{k_B{T}^2}$

So actually, squaring T* means that k_B is inadvertantly squared too. Hence the output is heat capacity of the entire system divided by boltzmanns constant. The output may be better described as reduced heat capacity. Also, the output energies are divided by N hence the need to multiply by N².

Looking at the graph (see fig. 9) shows that heat capacity decreases with increasing temperature and is lower for higher lattice spacing i.e. lower density and lower pressure. Since all systems have the same number of atoms (3375) they can be compared well (heat capacity is extensive).

The heat capacity depends on how well energy can be stored and hence on the accessible energy states: if a lot energy can be stored through excitations, the temperature doesn't rise (=high heat capacity). The temperature only rises when the energy is not being used for excitations i.e. if only few excitations are possible the heat capacity will be low. If much energy is being used for excitations this can mean two things: firstly, the energy spacing between levels might be large and every single excitation needs a lot of energy. Secondly, it may be that there simply are a lot of possible excitations (large number of degrees of freedom). Note that here, atoms are modeled and hence the only degrees of freedom are translational (assuming no electronic transitions).

In a dense system, where atoms are close to each other, the repulsive force that occurs when atoms are close to each other is felt more strongly. This means every translational transition is associated with higher energy and the heat capacity is high.
Heat capacity decreases with temperature because atoms have more kinetic energy at higher temperature and hence move faster. Therefore, intermolecular interactions are felt less strongly and it becomes easier to excite an atom into a higher translational state.

JC: Some good ideas. Heat capacity per volume increases with density because at high densities there are more atoms in a given volume. The change with temperature is harder to explain without more analysis, but you are right that as temperature increases, there is a higher density of energy levels in each energy interval.

This calculation did not include calculation of error however, it looks like there is some significant error in the calculation: even though the temperature was fixed it is expected to fluctuate as described, hence why the program is told to include average temperature in the output file. The fluctuation should be rather small, but he temperature in the output file differs greatly from what it was fixed to (only accurate to 2 significant figures; see table2). One of the more pronounced examples is T* = 2.6 (for sc=0.8). The value was set to 2.6 but the average temperature recorded in the output file is 2.648. This can be seen very well by close examination of the graph. The points should line up with the x ticks but they clearly don't. Interestingly, even though the output differs greatly from the input, this change is the same for sc=0.2 and sc=0.8. Taking the previous example again, the output for T*=2.6 and sc=0.2 is 2.646. This holds true for all cases.

Input temperature /uT* (both)	Output temperature /uT* for sc=0.2 ur*	Output temperature /uT* for sc=0.8 ur*
2.0	1.9734	1.9872
2.2	2.1740	2.1655
2.4	2.3860	2.3597
2.6	2.6465	2.6482
2.8	2.7572	2.7943

      Table 2: input and output temperatures

Structural properties and the radial distribution function

Task

Perform simulations of the Lennard-Jones system in the three phases. When each is complete, download the trajectory and calculate $g(r)$ and $\int g(r)\mathrm{d}r$. Plot the RDFs for the three systems on the same axes, and attach a copy to your report. Discuss qualitatively the differences between the three RDFs, and what this tells you about the structure of the system in each phase. In the solid case, illustrate which lattice sites the first three peaks correspond to. What is the lattice spacing? What is the coordination number for each of the first three peaks?

Figure 10: RDF and integral of RDF against reduced distance

The following conditions were chosen (table3) :

Phase	Spacing /ur*	Reduced Temperature /uT*	Unit Cell type
Solid	1.2	1.0	fcc
Liquid	0.8	1.2	sc
Gas	0.1	1.7	sc

      Table 3: Input parameters for RDF calculations

Results:

Gas		Liquid		Solid
Distance /ur*	Density /uρ*	Distance /ur*	Density /uρ*	Distance /ur*	Density /uρ*
1.1250	1.7953	1.0750	2.5212	1.0250	4.8984
1.8250	1.0374	2.0750	1.2066	1.4750	1.0000
1.9250	1.0291	3.0250	1.0596	1.8250	2.8762
2.1250	1.0332	3.9250	1.0199	2.1250	1.0365
2.2750	1.0307	4.9250	1.0073	2.3750	1.5738
2.4250	1.0259	5.3750	0.9964	2.7750	2.2869
2.6750	1.0159	5.8250	1.0029	3.1750	1.3860
2.825	1.0109	5.9750	1.0030	3.4750	0.8433

      Table 4: First 8 maxima in the RDF

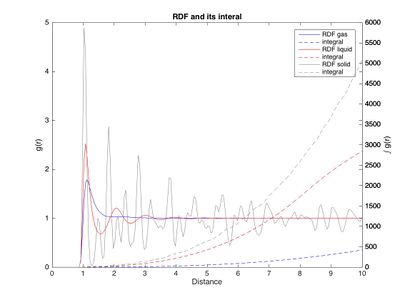
The RDF for a gas only shows one major peak at r = 1.125 σ u^r which is approximately the equilibrium bond length (r_eq = 2^1/6 σ u^r = 1.122σ u^r) in the Lennard-Jones potential (see table 4). This means that from the point of view of one atom, most of the "visible" atoms are at a distance of approximately 1.125 σ u^r, indicating that this is the main atomic spacing in a gas. The existence of a preferred atomic spacing indicates interaction between the atoms. Since the Lennard Jones potential is used, this is to be expected. However, in an ideal gas this would not be the case, where the RDF is constant. The presence of interactions in thee modeled system was previously observed in the calculations for density. Going further away from the central atom, the RDF is nearly constant, almost like a "blurred" environment of atoms that represents the bulk of other atoms. Some very small peaks are still found. These are not equally spaced and there seems to be no trend when it comes to intensity. The peaks represented by these atoms are in no particular order. They are randomly arranged. Overall, there is no long or short range ordering except for the one preferred interatomic separation.

In the liquid the largest peak is again approximately the equilibrium bond length. The RDF appears to have the shape of a damped oscillation, although the peak spacing varies slightly (and randomly). Every peak corresponds to a shell of atoms surrounding the central atom, with low atom density between the shells (represented by the valleys). The peak intensity decreases since the strength of the interactions decreases with distance. The shells become more diffuse until the distribution is random and the RDF becomes constant and 1. This indicates that while there is significant short range ordering and short range interactions, there is no long range ordering in a liquid, as expected. It should be possible to estimate the viscosity of a material from the RDF as a highly visous material has stronger long range interactions.

Figure 11: FCC lattice with neighbors marked. Atom X (red) is the reference atom. The green triangle shows how a can be calculated from atom A, the pink and red triangles show how atom C can be used to do so.

The solid shows very sharp peaks and deep valleys, indicating that the positions are very defined and only shake a little bit around the defined values, with little density between them. The first and largest peak at r*=1.0250 u^r_* corresponds to the next closest neighbor in the lattice (A in fig. 11). The next peaks at 1.4750 u^r_* and 1.8250 u_r^* to the next neighbors (B and C, respectively). It can be seen that there is a significant long range ordering in the lattice, by the fact that even at larger distances the RDF is not constant and still shows significant peaks.

The cell constant for the conventional unit cell, a_c, can be calculated from all three of these peaks (see fig. 11)
From atom B

$a^{*}=\overline{XB}=1.4750\mathrm{\sigma }{\mathrm{u}}_{\mathrm{r}}$

From atom A

$a^{*}=\sqrt{2}\times \overline{XA}=1.4495\mathrm{\sigma }{\mathrm{u}}_{\mathrm{r}}$

From atom C

$\stackrel{2}{\stackrel{‾}{XC}}=a^2+\stackrel{2}{\stackrel{‾}{BC}}$

$a^2=2\stackrel{2}{\stackrel{‾}{BC}}$

$a=\sqrt{\frac{2}{3}}\times \overline{CX}=1.4901\mathrm{\sigma }{\mathrm{u}}_{\mathrm{r}}$

Non of these values are exact but a good approximation. The exact value is (calculated from density in input file, see "equilibration"):

$a=\sqrt[3]{\frac{4}{1.2}}=1.4938\mathrm{\sigma }{\mathrm{u}}_{\mathrm{r}}$

JC: Good diagram to illustrate the position of the nearest neighbours and calculation to get the lattice constant from each peak.

Figure 12: RDF and integral, zoomed in Only showing first 3 peaks and cutoff

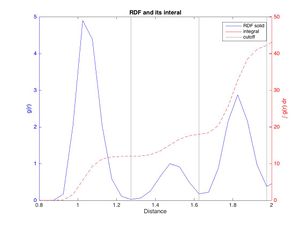
The integral of a peak corresponds to the number of atoms represented by it. Closely examining the RDF and running integral for the solid can be used to calculate the number of neighbors (see fig. 12). The minima between the peaks were taken as cutoff. It can be found by first finding the locations of the valleys left and right of the peak in the RDF, then finding their corresponding integrals and subtracting the running integral at the left hand valley from that at the right hand valley. Doing this gives integrals of approximately 12, 6.5 and 23.8, respectively. This indicates that every atom in the FCC is surrounded by 12 atoms of distance 1.49 σ u_r: these are the nearest neighbors. There are on average approximately 6.5 atoms of distance B and 24 atoms of distance C.

JC: Good idea to plot the RDF and integral on the same axes. How many atoms should there be for the first, second and third nearest neighbours? You should be able to count them using the structure of the fcc lattice and compare this to the number that you get from the integral.

The first peak is the largest for all, however it is much larger for liquid than for gas and even bigger for a solid. The same trend is seen for the integral, which, compared to the gas, is roughly twice as large for a liquid and 4 times as large for a solid. This corresponds to the increasing density going from gas via liquid to solid (more neighbors in the RDF hence higher peak hence larger integral).

For all atoms the RDF falls to zero quickly as atoms get close, showing some minimum separation between atoms. This can be explained by the high repulsion at close distances as described in the LJ potential. Furthermore, LAMMPS assigns a diameter of 1 u_r^* to the atoms by default, meaning that they will clash at distances closer than 1 u_r^* and atoms cannot get closer to each other. It has been observed that the peaks in the RDF get broader as temperature increases, indicating thermal motion.

Dynamical properties and the diffusion coefficient

Background and Methods

Task
Make a plot for each of your simulations (solid, liquid, and gas), showing the mean squared displacement (the "total" MSD) as a function of timestep. Are these as you would expect? Estimate $D$ in each case. Be careful with the units! Repeat this procedure for the MSD data that you were given from the one million atom simulations.

Task

Use the trapezium rule to approximate the integral under the velocity autocorrelation function for the solid, liquid, and gas, and use these values to estimate $D$ in each case. You should make a plot of the running integral in each case. Are they as you expect? Repeat this procedure for the VACF data that you were given from the one million atom simulations. What do you think is the largest source of error in your estimates of D from the VACF?

All simulations were run using a timestep of 0.002. The individual parameters are as follows (table).:

Phase	Density /uρ*	Reduced Temperature /uT*	Unit Cell
Solid	1.2	1.0	fcc
Liquid	0.8	1.2	sc
Gas	0.2	1.8	sc

      Table 5: Conditions for diffusion coefficient simulations

A note on units and dimensions

Diffusion coefficient has the dimensions $\frac{r^2}{t}$ (distance squared or area per time) and hence the SI unit is ${\mathrm{m}}^{\mathrm{2}}{\mathrm{s}}^{\mathrm{-}\mathrm{1}}$. The simulations however use reduced distance and reduced time hence the dimensions will be $\frac{r^{*2}}{t^{*}}$ with the unit $u_{{\mathrm{r}}^{\mathrm{*}}}^{\mathrm{2}}{u}_{{\mathrm{t}}^{\mathrm{*}}}^{\mathrm{-}\mathrm{1}}$ ("unit of reduced distance squared divided by unit of reduced time"). To avoid this awkward unit, the (made up) unit ${\mathrm{u}}_{\mathrm{D}}\mathrm{=}{u}_{{\mathrm{r}}^{\mathrm{*}}}^{\mathrm{2}}{u}_{{\mathrm{t}}^{\mathrm{*}}}^{\mathrm{-}\mathrm{1}}$ (unit for diffusion coefficient) is used here. To convert the diffusion coefficient into SI units one would need to know the Lennard-Jones parameters ε and σ for the system:

$r^{*}=\frac{r}{\sigma }\iff r=r^{*}\sigma$

$t^{*}=\frac{t}{\sigma \sqrt{\frac{ϵ}{m}}}\iff t=t^{*}\sigma \sqrt{\frac{ϵ}{m}}$    

hence D can be converted into SI units using:

$D_{SI}=\frac{r^2}{t}=D\times \frac{r^{*2}\sigma }{\sqrt{\frac{ϵ}{m}}}$

Therefore, the diffusion coefficient calculated here may be better referred to as "reduced diffusion coefficient".

Furthermore, the output for the x values will be in number of timesteps rather than (reduced) time. Note also that number of timestep is equivalent to time, t, divided by the spacing, dt, between timesteps.

The slope of the MSD graph will have the dimensions

$\frac{r^{*2}dt}{t}$

and hence will need to be divided by dt = 0.002.

The VACF has the dimensions

$v^2=(\frac{\partial r}{\partial t}{)}^2$

It's integral therefore will have the dimensions

$\int (\frac{\partial r}{\partial t}{)}^{2}dt=\frac{r^2}{t}dt$

and will need to be multiplied by dt = 0.002 u_t^*.

JC: Great, you are very careful in keeping track of units.

Velocity Autocorrelation Function

Task

In the theoretical section at the beginning, the equation for the evolution of the position of a 1D harmonic oscillator as a function of time was given. Using this, evaluate the normalised velocity autocorrelation function for a 1D harmonic oscillator (it is analytic!): $C\left(\tau \right)=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}v\left(t\right)v(t+\tau )\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{v}^2\left(t\right)\mathrm{d}t}$ Be sure to show your working in your writeup. On the same graph, with x range 0 to 500, plot $C\left(\tau \right)$ with $\omega =1/2\pi$ and the VACFs from your liquid and solid simulations. What do the minima in the VACFs for the liquid and solid system represent? Discuss the origin of the differences between the liquid and solid VACFs. The harmonic oscillator VACF is very different to the Lennard-Jones solid and liquid. Why is this? Attach a copy of your plot to your writeup.

Velocity of the simple harmonic oscillator as a function of t is given by:

$v(t)=\frac{\partial x(t)}{\partial t}=\frac{\partial }{\partial t}[A\cos (\omega t+\varphi )]=-A\omega \sin (\omega t+\varphi )$

Hence, as a function of t + τ

$v(t+\tau )=\frac{\partial x(t+\tau )}{\partial (t+\tau )}=\frac{\partial }{\partial (t+\tau )}[A\cos (\omega (t+\tau )+\varphi )]=-A\omega \sin (\omega (t+\tau )+\varphi )$

Substituting into the velocity autocorrelation function gives:

$C\left(\tau \right)=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{A}^2{\omega }^2\sin (\omega t+\varphi )\sin (w(t+\tau )+\varphi )\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{A}^2{\omega }^2{\sin }^2(wt+\varphi )\mathrm{d}t}$

Which can be rewritten as:

$C\left(\tau \right)=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\sin (\omega t+\varphi )\sin ((\omega t+\varphi )+\omega \tau ))\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{\sin }^2(\omega t+\varphi )\mathrm{d}t}$

It is now apparent that the trigonometric identiy for addition can be used to expand the sine:

$C\left(\tau \right)=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\sin (\omega t+\varphi )(\sin (\omega t+\varphi )\cos (\omega \tau )+\cos (\omega t+\varphi )\sin (\omega \tau ))\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{\sin }^2(\omega t+\varphi )\mathrm{d}t}$

Expanding the equation and splitting the fraction into a sum of two gives:

$C\left(\tau \right)=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{\sin }^2(\omega t+\varphi )\cos (\omega \tau )\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{\sin }^2(\omega t+\varphi )\mathrm{d}t}+\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\sin (\omega t+\varphi )\cos (\omega t+\varphi )\sin (\omega \tau )\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{\sin }^2(\omega t+\varphi )\mathrm{d}t}$

Since cos(ω τ) is not a function of t it can be treated as a constant and taken out of the integration:

$C\left(\tau \right)=\cos (\omega \tau )\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{\sin }^2(\omega t+\varphi )\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{\sin }^2(\omega t+\varphi )\mathrm{d}t}+\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\sin (\omega t+\varphi )\cos (\omega t+\varphi )\sin (\omega \tau )\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{\sin }^2(\omega t+\varphi )\mathrm{d}t}$

No integration is required: the first fraction equals 1 (N.B. same integral in denominator and numerator). Both integrals of the second term are nonconvergent and can be set to zero: if they were integrated they would still be functions of sine and cosine. Approaching them from opposite limits yields different results.

JC: Why can the integrals be set to zero? The integral of sin^2 in the denominator is not zero. The integrand in the numerator is an odd function and the limits of the integral are symmetric about zero so this integral is zero.

Hence, the result will simply be:

$C\left(\tau \right)=\cos (\omega \tau )$

Results and Discussion

Figure 13: VACF

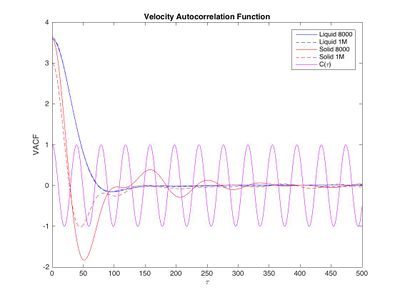
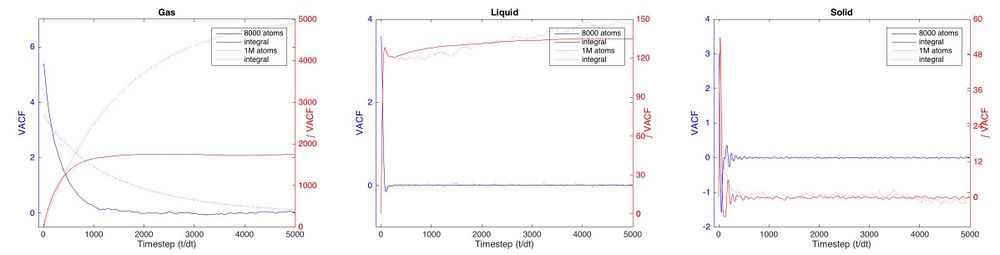
The VACF gives the correlation of the particle's position with its initial position as a function of time. If the particle was in a vacuum, unobstructed by anything, the VACF would be constant and high since the its velocity would not change and hence be the same as the initial velocity. If the particle attempts to travel through something that's not vacuum, it's velocity will change due to interactions with other particles. In an extreme case the particle will collide with another particle and deflect. The sign of the velocity changes as it "bounces back" and the VACF will be negative. The particle doesn't even have to hit another particle, it may just feel attraction or repulsion to other atoms, which will change it's velocity too. For any material the VACF will be flat at first until the particle hits another particle or feels the attraction of another particle. It will then fall initially as it hits other atoms and eventually become zero since it 'forgets' it's initial position. How fast it decorrelates depends on the strength and frequency of the interactions. In a gas, having low density, the VACF will slowly decay. As seen in figure 14, this happens over the first 1000 timesteps. In a liquid or solid, the interactions are stronger since the particle is closer to other particles. Figure 13 shows that for a liquid the VACF falls rapidly in the first 75 timesteps as it feels strong forces from other particles. It briefly goes below zero, hitting another particle hence changing the sign of it's velocity and then eventually becoming uncorrelated. This cannot be seen in the plot but finding and plotting peak height against peak positions shows that even at larger distances the correlation doesn't fall to zero as expected. This may be the computational error of the program, however, it can be seen that both for solid and liquid the correlation is larger in the larger system. If it was a computational error, the error would be smaller for a larger system. Perhaps more interesting is the VACF for a solid which, definitely shows the behavior of a damped oscillator. It falls to negative values slightly earlier than the liquid because it is denser and hits other atoms faster. Comparing decay time of solid, liquid and gas, the difference is larger between gas and all others than between liquid and solid corresponding to the fact that a solid and liquid have more similar densities than a liquid and gas. The particle in the solid keeps hitting other particles hence going to negative regions periodically. This corresponds to the vibration within the lattice. Theoretically, the VACF should therefore be an oscillation with maximum at the first timestep (cosine function, see fig. 13). The fact that is not, is because other forces act on the particle and create imperfections in the regular vibration. The particle becomes less correlated and the extreme values in the VACF decay (damped oscillator) until it eventually reaches zero, when the particle is decorrelated.

JC: Good understanding of VACF, what about the VACF of the harmonic oscillator?

As the VACF is a measure of interatomic interactions, it can be used to calculate diffusion.

The diffusion coefficient

As expected, the diffusion coefficient is largest for a gas (few collisions hence fast diffusion), much smaller for liquid (very dense, collide often) and zero for a solid (constrained to a lattice). Visualizing the trajectory shows fast movement for all three however, for liquid and gas the atoms move around and change position and hence diffuse. For the solid the atoms shake around on the spot, moving in all 3 dimensions but atoms do not change position with each other.

Figure 14: Trendlines are the thin lines. It may be necessary to view the graphs in full resolution to see all details.

Figure 15: VACF VACF and integral VACF vs timestep for 8K and 1M atoms, sol, liquid, gas.

The following results were obtained:

Phase	D / uD using MSD	D / uD using VACF	Difference uD using MSD	Difference as percentage of larger value /%
Gas* (8000 atoms)	1.2087	1.1687	0.0400	3.3
Gas (1M atoms)	3.0158	3.2685	0.2526	7.7
Liquid (8000 atoms)	0.0850	0.0901	0.0051	5.6
Liquid (1M atoms)	0.0886	0.0979	0.0093	9.5
Solid (8000 atoms)	0.0000	0.0002	0.0002	n/a
Solid (1M atoms)	0.0000	0.0000	0.0000	n/a

      Table 6: Results for Diffusion coefficient using both methods.
      * T* = 1.8 /u_t^*, ρ* = 0.2 /u_ρ^*

The mean suqared displacement for a timestep is calculated by squaring the diplacement of each atom and then summing them up (the total displacement of the system will be approximately zero as it is confiend to a box and some particles move one way, some the other way hence the squares must be used for the summation). The MSD is added to that for the previous timestep (like a running summation). The final MSD is proportional to the total distance explored by the "average particle" over the course of the simulation. It is hence also proportional to the diffusion coefficient (diffusion is movement of a particle). Assuming particles move by the same ammount in every timestep, plotting MSD against time will give a straight line. This can be seen very well in a gas or liquid. There is some visible discrepancy from linearity for a gas. This is because when the atoms are first assigned a velocity, they move linearly until they collide. If they move in a straight line their displacement will be linearly dependent on time and hence displacement squared gives a parabola shaped curve. It's only when the particles collide that they transfer momentum and move in the random fashion described by Brownian motion.

Figure 16: MSD for first 500 timesteps

While this is the case in all phases, it is not significant for other phases because of the higher density and hence short collision time. This is confirmed by the fact that increasing the pressure of the gas makes this non linearity disappear faster (see fig. 15).

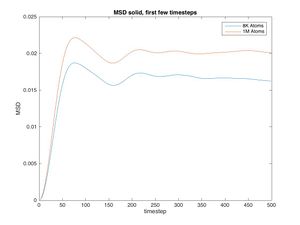
In the solid there should not be any displacement as the particles are assigined to a regular lattice. In reality some fluctuation can be seen throughout the system. Though the fluctuatins after 1000 timeseteps are small and may just be error, the early fluctuations are signifficant (see fig. for an enlarged in version of just the first 500 timesteps).

In the first 76 timesteps the MSD of the system increases in a nearly parabolic shape, for the same reason as before (note that even though the denisty is high, there are few collisions as the atoms have fixed positions, hence the velocities take some time to adjust). What happens next is strange: the MSD falls and oscillates (damed). Seeing as the MSD is a running summation of positive values, it should not be allowed to decrease at any point. Some fluctuations are seen throughout the experiment which may be error but the fluctuatins seen here are defineitly not random and their magnitude exceeds those that might be error.

JC: MSD can reduce if particles move back towards their starting position, it will go to zero if after a certain time all particles return to their starting positions.

After about 1000 timesteps the overall displacement is zero, the curve becomes constant (with some error) and the slope of the MSD graph falls to zero.

Fig. 17: First 2000 timesteps for MSD of gas with trendline (trendline plotted using last 3000 timesteps to which is the linear part and not displayed here). Going down, temperature decreases, going right density decreases.

For the gas the output greatly depends on the exact conditions. As seen in table 6, diffusion gets facilitated with increasing temperature (faster movement of atoms) and decreasing density (fewer collisions).

The same calculations also showed that the non linear part at the beginning lasts over more timesteps at low density. This increases collision time, confirming the aforementioned theory. Temperature appears to increase the duration of nonlinearity very slightly. Theoretically increasing temperature should increase frequency of collisions (atoms move faster) and hence shorten the duration of nonlinearity. It is hard to prove or disproof this using the graphs since the temperature difference is very small.

It is therefore hard to compare the 1M atom system to the 8000 atom system without knowing the exact conditins that were used for the 1M system.

Another simulation was run at ρ*=0.4 u_ρ^* and T*=2.0 u_T^*. Interestingly, the diffusion coefficient for this was approximately 0.6 u_D (0.5949 u_D and 0.5672 u_D for MSD and VCAF, respectively). This value is between liquid and gas but since it is not in the same order of magnitude of either it is highly unlikely that it is one of them. This may represent a supercritical fluid with properties in-between liquid and gas.

JC: What phase should be present at these conditions based on the phase diagram?

Such a pressure dependence is not expected in liquids as their compressibility is very low. A similar temperature dependence is expected. In solids the diffusion coefficient will always be zero.

D	T* = 1.7 uT*	T* = 1.8 uT*
ρ* = 0.1 uT*	2.3245 uD	2.4376 uD
ρ* = 0.2 uT*	1.1534 uD	1.2087 uD

      Table 7: Diffusion coefficient for a gas at different temperatures and pressures. Calculated using MSD. Using VACF the values are similar.

Errors

There are two possible sources of error: the simulation and the analysis. The biggest source of error for D using VCAF is the approximation of the integral. This was estimated using the trapezium rule, applied to every timestep. Considering that the timesteps are very small the estimate should be fairly good (the curve was essentially split into 5000 parts). For D using MSD, the analysis related error is the fitting of the curve. The last 3000 values were taken for the slope to avoid error due to the nonlinear part at the beginning. This was decided by optical examination of the plots: the largest non linearity is seen for gas which in all cases behaved linearly after 2000 timesteps. The same cutoff was applied to all slopes for consistency, even though the system clearly settles much earlier for the other phases. The R² was greater than 0.9999 for all curves except the solid using 1M atoms (for that it was 0.3621). 0.9999 is very good for 3000 points.

Another source of error is the simulation. This is definitely more accurate for larger systems (even if the R² was less good for the solid). As discussed previously, this could also be made more accurate by using a smaller timestep. Both (large system, small timestep) are computationally expensive.

The values were rounded to the 4^th decimal place. Showing all available decimal places, D for the solid is 0.000002314557236 u_D using 8000 atoms and -0.000004208364482 u_D using 1M atoms using MSD. Using VACF the values are: 0.000188095911153 u_D and -0.000007762365573 u_D. The fact that both methods give a negative diffusion coefficient for the 1M simulation indicates that this error originates from an imperfection in the simulation rather than the analysis.

The relatively small difference between the different methods, especially for solid and liquid, indicates that all assumptions that are made were appropriate.

The very small difference between the 8000 atom and 1M atom atom systems for the solid indicates that a small system is sufficient to model the diffusion in a solid (or rather, to proof that there is no diffusion and the solid is indeed a crystal). For the liquid both systems give relatively similar results too, indicating that a system of 1M atoms is not required. For the gas such a comparison cannot be made since, as discussed before, one would need to know the exact conditions of the large system.

The last set of experiments (different conditions for gas) should really have been done using more conditions as it is very risky to make a scientific conclusion based on such little. An interesting but time consuming expansion could be to vary temperature at constant density and density at constant temperature over several points to draw a more representative graph. However, the four findings illustrate this concept very well and hence were included. The VACF was integrated for two of the four conditions and corresponded well to the MSD results (within the expected error), showing the same trends. Hence, it was assumed they would show the same trends for all conditions and not all were analyzed.

JC: Good, thorough analysis of the possible errors.

Conclusion

It was shown that using molecular dynamics a whole range of thermodynamic properties for solid, liquid and gas can be calculated to very high accuracy.. First an appropriate timestep for the simulations were determined by trying different values and finding a compromise between computational cost and accuracy. Using this timestep, the pressure and temperature dependence of the density and heat capacity of a gas were found and compared to an ideal gas. Furthermore, the arrangement of atoms in a solid, liquid and gas were found and even the lattice spacing could be determined to a reasonable accuracy. Finally, diffusion in solid, liquid and gas were modeled and the pressure dependence in a gas was determined.