Talk:Mod:TBLS1115

Theophile Baissas Liquid Simulations Experiment

NJ: General comments: Lovely report, very thorough. Some good insights into the harder questions at the end, too.

INTRODUCTION TO MOLECULAR DYNAMICS SIMULATIONS

TASK: Open the file HO.xls. In it, the velocity-Verlet algorithm is used to model the behaviour of a classical harmonic oscillator. Complete the three columns "ANALYTICAL", "ERROR", and "ENERGY": "ANALYTICAL" should contain the value of the classical solution for the position at time t, "ERROR" should contain the absolute difference between "ANALYTICAL" and the velocity-Verlet solution (i.e. ERROR should always be positive -- make sure you leave the half step rows blank!), and "ENERGY" should contain the total energy of the oscillator for the velocity-Verlet solution. Remember that the position of a classical harmonic oscillator is given by $x(t)=Acos(\omega t+\varphi )$ (the values of A, $\omega$, and $\varphi$ are worked out for you in the sheet).

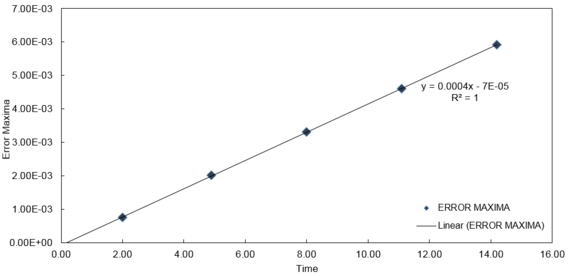
TASK: For the default timestep value, 0.1, estimate the positions of the maxima in the ERROR column as a function of time. Make a plot showing these values as a function of time, and fit an appropriate function to the data.

TASK: Experiment with different values of the timestep. What sort of a timestep do you need to use to ensure that the total energy does not change by more than 1% over the course of your "simulation"? Why do you think it is important to monitor the total energy of a physical system when modelling its behaviour numerically?

The ANALYTICAL value is calculated using the full steady state equation of the harmonic oscillator motion

$x(t)=Acos(\omega t+\varphi )$.

With $A=1$, $\omega =1$, and $\varphi =0$.

Additionally $\omega =\sqrt{(\frac{k}{m})}=\frac{2\pi }{T}$

The initial conditions given were: $k=1.00$, $timestep=0.100$,$mass=1.00$, $A=1.00$, $\omega =1.00$

Figure 1 demonstrates the results from the velocity-Verlet alorithm for the position of the oscillator and from the classical calculation are in good agreement.

Figure 1: Analytical Solution against Time

The ERROR value gives the difference between the ANALYTICAL value and x(t), the position given by the velocity-Verlet algortihm at time t. It varies periodically and is small compared to the actual values which are contained in the interval [-1,1]. It does however gain amplitude with time with the error maxima increasing linearly. The gradient of this variation of the error maxima is found to be $4.22\times 10^{-4}$.

File:Error fit TBLS1115.PNG

Figure 2: Error against Time

Figure 3: Linear Fit to the Error maxima

The ENERGY value is calculated by summing the potential and kinetic energy of the system.

$E=\frac{1}{2}m{v}^2+\frac{1}{2}k{x}^2$

Figure 4: Total Energy against Time

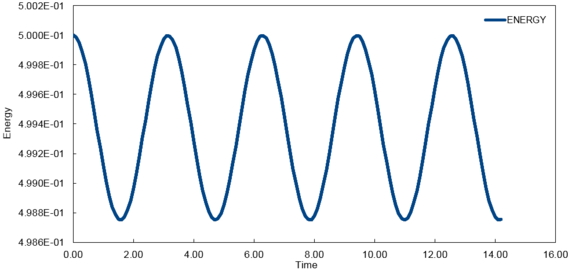
In an ideal harmonic oscillator, the total energy of the system can be expected to remain constant as nothing is lost to the surroundings, thus giving perpetual motion through cycles of extension and compression with the interchange between potential and kinetic energy. It is found here that the total energy has a constant average over time. It does however oscillate slightly around this average, following a periodic sinusoidal behaviour. The oscillations are extremely small in amplitude, only 0.12% of the average value and the model can therefore be considered to be sufficiently close to the expected behaviour.

By experimenting with different timesteps, it can be found that a timestep shorter than 0.28 seconds is necessary for the total energy of the system to stay within 1% of its average value. It is important to monitor this total energy to verify that the system simulated does indeed correspond to a closed system with a constant total energy.

TASK: For a single Lennard-Jones interaction, $\varphi \left(r\right)=4ϵ(\frac{{\sigma }^{12}}{r^{12}}-\frac{{\sigma }^6}{r^6})$, find the separation, $r_0$, at which the potential energy is zero. What is the force at this separation? Find the equilibrium separation, $r_{eq}$, and work out the well depth ($\varphi \left(r_{eq}\right)$). Evaluate the integrals $\underset{2\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)\mathrm{d}r$, $\underset{2.5\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)\mathrm{d}r$, and $\underset{3\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)\mathrm{d}r$ when $\sigma =ϵ=1.0$.

$r_0=\sigma$ ${\displaystyle }$ is the separation at which the $r^{-}12$ term corresponding to short range repulsion and the $r^{-}6$ term corresponding to long range attraction between the pair of atoms cancel each other out to give a zero potential energy.

The force is given by

$\mathbf{F}=-\frac{\mathrm{d}\varphi \left(\mathbf{r}\right)}{\mathrm{d}\mathbf{r}}$

$-\frac{\mathrm{d}\varphi \left(\mathbf{r}\right)}{\mathrm{d}\mathbf{r}}=4ϵ(\frac{12{\sigma }^{12}}{r^{13}}-\frac{6{\sigma }^6}{r^7})$

with

$r_0=\sigma$

,

$F(r_0)=\frac{24ϵ}{\sigma }$

The equilibrium separation is the separation $r_e$ for which $-\frac{\mathrm{d}\varphi \left({\mathbf{r}}_{\mathbf{e}}\right)}{\mathrm{d}\mathbf{r}}=0$

Therefore

$(\frac{12{\sigma }^{12}}{r_e^{13}}=\frac{6{\sigma }^6}{r_e^7})$

$2{\sigma }^6=r_e^6$

$r_{e}q=2^{\frac{1}{6}}\sigma$

Thus

$\varphi \left(r\right)=4ϵ(\frac{{\sigma }^{12}}{2^2{\sigma }^{12}}-\frac{{\sigma }^6}{2{\sigma }^6})$

$\varphi \left(r\right)=4ϵ(\frac{1}{4}-\frac{1}{2})$

$\varphi \left(r\right)=-ϵ$

Evaluating integrals when $\sigma =ϵ=1.0$.

$\underset{2\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)\mathrm{d}r\simeq -0.025$

$\underset{2.5\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)\mathrm{d}r\simeq -0.008$

$\underset{3\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)\mathrm{d}r\simeq -0.003$

NJ: Show a bit more working.

TASK: Estimate the number of water molecules in 1ml of water under standard conditions. Estimate the volume of $10000$ water molecules under standard conditions.

There are approximately $3.34\times 10^{22}$ molecules in 1mL of water under standard conditions. This is calculated using Avogadro's number and the density of water which is $\rho =999.8\times 10^{-1}g.c{m}^{-3}$ under standard conditions.

Using these same numbers, the volume of 10000 water molecules under standard conditions can be calculated and it is approximately $3.0\times 10^{-}19mL$.

TASK: Consider an atom at position $(0.5,0.5,0.5)$ in a cubic simulation box which runs from $(0,0,0)$ to $(1,1,1)$. In a single timestep, it moves along the vector $(0.7,0.6,0.2)$. At what point does it end up, after the periodic boundary conditions have been applied?.

After the periodic boundary conditions have been applied, this atom ends up at position $(0.2,0.1,0.7)$.

TASK: The Lennard-Jones parameters for argon are $$\begin{gathered} \sigma =0.34\mathrm{n}\mathrm{m},ϵ \\ / \\ {k}_B=120\mathrm{K} \end{gathered}$$. If the LJ cutoff is $r^{*}=3.2$, what is it in real units? What is the well depth in $$\begin{gathered} {\mathrm{k}\mathrm{J} \\ \mathrm{m}\mathrm{o}\mathrm{l}}^{-1} \end{gathered}$$? What is the reduced temperature $T^{*}=1.5$ in real units?

If $r^{*}=3.2$, $r=r^{*}\times \sigma =1.09nm$.

The well depth is $ϵ=120K\times k_B$. So $ϵ=1.66\times 10^{-21}J\simeq 1.0kJmo{l}^{-1}$

Finally, $T=120T^{*}=180K$

Reduced units are used throughout all the different simulations and all the graphs presented have axis expressed in reduced units.

EQUILIBRATION

TASK: Why do you think giving atoms random starting coordinates causes problems in simulations? Hint: what happens if two atoms happen to be generated close together?

Giving atoms random coordinates can cause problems in simulations as it can create situations that are physically impossible and lead to absurd values. For instance, atoms could initially be placed too close to each other which given the equation for the Lennard-Jones potential could lead to extremely high energy potentials that do not actually occur in real systems.

NJ: What is the impact of the very high potential energy?

TASK: Satisfy yourself that this lattice spacing corresponds to a number density of lattice points of $0.8$. Consider instead a face-centred cubic lattice with a lattice point number density of 1.2. What is the side length of the cubic unit cell?

File:Cubib lattice.PNG

Figure 5: Simple Cubic Lattice

A simple cubic unit cell contains a single atom. With a lattice spacing of 1.07722, the unit cell has a volume $V=1.07722^3=1.25$ Therefore: $\rho =\frac{1}{1.25}=0.8$

File:Fcc latt.PNG

Figure 6: Face Centred Cubic Lattice

The side length of a face-centred cubic lattice with a lattice point number density of 1.2 is $\sqrt[3]{\frac{4}{d}}=1.49$

TASK: Consider again the face-centred cubic lattice from the previous task. How many atoms would be created by the create_atoms command if you had defined that lattice instead?

There would be a total of 4000 atoms created by the create_atoms command if the lattice defined was fcc (4 atoms per unit cell).

TASK: Using the LAMMPS manual, find the purpose of the following commands in the input script:

mass 1 1.0
pair_style lj/cut 3.0
pair_coeff * * 1.0 1.0

The mass command defines the mass of the different atom types simulated. Here there is only one type and it is given a mass of 1.0.

Pair_styl lj/cut is used to calculate the Lennard-Jones potential between pairs of atoms. The cut (3.0 here) gives the argument for the global cutoff for the Lennard-Jones interactions in distance units.It is the maximal distance for which the Lennard-Jones interaction between pair of atoms will be computed.

Pair_coeff is used to specify the pairwise force field coefficients. The asterix is here to signify this applies to all pairs of atoms (and atom types, only one here) present in the box.

NJ: What are the coefficients in this case?

TASK: Given that we are specifying ${\mathbf{x}}_i\left(0\right)$ and ${\mathbf{v}}_i\left(0\right)$, which integration algorithm are we going to use?

The integration algorithm that will be used is the velocity Verlet algorithm since it requires $x_i\left(0\right)$ and $v_i\left(0\right)$ for the computation to be initiated.

TASK: Look at the lines below.

### SPECIFY TIMESTEP ###
variable timestep equal 0.001
variable n_steps equal floor(100/${timestep})
variable n_steps equal floor(100/0.001)
timestep ${timestep}
timestep 0.001

### RUN SIMULATION ###
run ${n_steps}
run 100000

The second line (starting "variable timestep...") tells LAMMPS that if it encounters the text ${timestep} on a subsequent line, it should replace it by the value given. In this case, the value ${timestep} is always replaced by 0.001. In light of this, what do you think the purpose of these lines is? Why not just write:

timestep 0.001
run 100000

This makes it easier to change the timestep in future copies of the code. The variable's value can simply be changed in the line where the variable is defined. All other lines which call this value will not need to be updated as they call the variable to which the new value is attached.

NJ: This section makes sure that you always simulate the same time (nsteps*dt), no matter what timestep is chosen.

TASK: make plots of the energy, temperature, and pressure, against time for the 0.001 timestep experiment (attach a picture to your report). Does the simulation reach equilibrium? How long does this take? When you have done this, make a single plot which shows the energy versus time for all of the timesteps (again, attach a picture to your report). Choosing a timestep is a balancing act: the shorter the timestep, the more accurately the results of your simulation will reflect the physical reality; short timesteps, however, mean that the same number of simulation steps cover a shorter amount of actual time, and this is very unhelpful if the process you want to study requires observation over a long time. Of the five timesteps that you used, which is the largest to give acceptable results? Which one of the five is a particularly bad choice? Why?

File:0.001equilibration.JPG

Figure 7: Equilibration of Parameters for a Timestep of 0.001

File:Closeup2.PNG

Figure 8: Equilibration of Parameters for a Timestep of 0.001 Close Up

The simulation reaches equilibrium for all the studied parameters after a time 0.4. This can be observed when zooming in on the relevant region of the graphs.

File:Engvariationdifftimesteps.JPG

Figure 9: Energy Variation For Different Timesteps

File:Engvartimestepcloserup.PNG

Figure 10: Energy Variation For Different Timesteps Close Up

A timestep of 0.015 is a particularly bad choice as the system does not equilibrate and the total energy shoots off after a certain time.The largest timestep to give acceptable results is 0.01. For all timesteps under this value, the simulation reaches equilibrium. However, for a better accuracy a timestep of 0.0025 is the best option since the value around which the equilibrium oscillates is slightly lower and matches that of a 0.001 timestep very closely.

RUNNING SIMULATION UNDER SPECIFIC CONDITIONS

TASK: Choose 5 temperatures (above the critical temperature $T^{*}=1.5$), and two pressures (you can get a good idea of what a reasonable pressure is in Lennard-Jones units by looking at the average pressure of your simulations from the last section). This gives ten phase points — five temperatures at each pressure. Create 10 copies of npt.in, and modify each to run a simulation at one of your chosen $(p,T)$ points. You should be able to use the results of the previous section to choose a timestep. Submit these ten jobs to the HPC portal. While you wait for them to finish, you should read the next section.

The time step chosen is 0.0025. The two pressures chosen were $2.5$ and $3.0$ and the temperature range studied was $1.5,2.0,2.5,3.0,5.0$.

TASK: We need to choose $\gamma$ so that the temperature is correct $T=\mathfrak{𝔗}$ if we multiply every velocity $\gamma$. We can write two equations: $\frac{1}{2}\sum _i{m}_i{v}_i^2=\frac{3}{2}N{k}_{B}T$

$\frac{1}{2}\sum _i{m}_i{\left(\gamma v_i\right)}^2=\frac{3}{2}N{k}_B\mathfrak{𝔗}$

Solve these to determine $\gamma$.

By factorising ${\gamma }^2$ out of the sum and combining the two equations we find: $\gamma =\sqrt{\frac{\mathfrak{𝔗}}{T}}$

NJ: Show a bit more working.

TASK: Use the manual page to find out the importance of the three numbers 100 1000 100000. How often will values of the temperature, etc., be sampled for the average? How many measurements contribute to the average? Looking to the following line, how much time will you simulate?

The fix command allows us to calculate the average for any variable (thermodynamic property) previously defined. It is followed by the numbers 100 1000 100000 which indicate how the averaging should be performed.

The first value corresponds to Nevery which tells the program how often (in timesteps) it must take a sample value to calculate the average for the parameter in question. The second value Nrepeat gives the number of samples included in the final average. Finally, Nfreq=100000 and its multiples are the values for which the average quantities will be generated.

Since we are looking at 100000 data points this effectively means that the average over the entire data set is calculated from values sampled every 100 data points.

The timestep has been set to 0.0025. Simulating 100000 data points means 250 reduced time units will be simulated.

Plotting the Equations of State

TASK: When your simulations have finished, download the log files as before. At the end of the log file, LAMMPS will output the values and errors for the pressure, temperature, and density $\left(\frac{N}{V}\right)$. Use software of your choice to plot the density as a function of temperature for both of the pressures that you simulated. Your graph(s) should include error bars in both the x and y directions. You should also include a line corresponding to the density predicted by the ideal gas law at that pressure. Is your simulated density lower or higher? Justify this. Does the discrepancy increase or decrease with pressure?

The density predicted by the ideal gas law was computed using the definition $pV=N{k}_{B}T$ which gives $\frac{N}{V}=\frac{p}{k_{B}T}$ with $k_B=1$ when performing calculations in reduced units.

File:Eqstateplot.PNG

Figure 11: Plotting Equations of State

The simulated density is lower than the density predicted by the ideal gas law at any given pressure and temperature. This is due to the difference between the liquid that is simulated and an ideal gas. In an ideal gas, particles are considered not to interact except when they collide elastically.

NJ: Actually, ideal gas atoms don't collide at all - it's the van-der-Waals gas that has elastic collisions between hard spheres.

This means the Lennard Jones interactions are set to zero and the $r^{-12}$ internuclear repulsion term is not taken into account. However, for the liquid simulation it is included and as a result the atoms are found further apart thus lowering the density.

The discrepancy increases with pressure. This is again due to the fact that in an ideal gas, particles do not interact, whereas in the liquid system simulated, the particles which are pushed closer together at high pressure repel each other more strongly. Thus the difference between the densities predicted becomes greater.

On a different note, increasing the temperature leads to a convergence of the values obtained by the simulation and those predicted by the ideal gas law. Because of the increased thermal motion, the kinetic energy becomes predominant at higher temperatures. As a result, the intermolecular repulsions become more negligible meaning that the behaviour of the liquid effectively tends towards that of an ideal gas. Its density becomes proportional to the inverse of the temperature.

CALCULATING HEAT CAPACITIES USING STATISTICAL PHYSICS

Many quantities in statistical thermodynamics can be calculated by considering how far the system is able to fluctuate from its average equilibrium state. For example, if the temperature is held "constant", then we know that the total energy must be fluctuating. The magnitude of these fluctuations actually tell us about the heat capacity of the system, according to the equation:

$C_V=\frac{\partial E}{\partial T}=\frac{\mathrm{V}\mathrm{a}\mathrm{r}\left[E\right]}{k_B{T}^2}=N^2\frac{⟨E^2⟩-{⟨E⟩}^2}{k_B{T}^2}$

$\mathrm{V}\mathrm{a}\mathrm{r}\left[E\right]$ is the variance in $E$, $N$ is the number of atoms, and it is a standard result from statistics that $\mathrm{V}\mathrm{a}\mathrm{r}\left[X\right]=⟨X^2⟩-{⟨X⟩}^2$. The $N^2$ is required because LAMMPS divides all energy output by the number of particles (so when you measure $E$, you are actually measuring $E/N$).

TASK: As in the last section, you need to run simulations at ten phase points. In this section, we will be in density-temperature $({\rho }^{*},T^{*})$ phase space, rather than pressure-temperature phase space. The two densities required at $0.2$ and $0.8$, and the temperature range is $2.0,2.2,2.4,2.6,2.8$. Plot $C_V/V$ as a function of temperature, where $V$ is the volume of the simulation cell, for both of your densities (on the same graph). Is the trend the one you would expect? Attach an example of one of your input scripts to your report.

The formula above was used in the input script to calculate Cv.

File:CvvT.PNG

Figure 12: Heat Capacity over Volume variations with Time

File:InputFilenvt0.2d2.2t.PNG

Figure 13: Input File for 0.2d and 2.2T

The trend observed corresponds to what could be expected. Logically, $\frac{C_v}{V}$ increases with density at a given temperature. Indeed, the amount of energy required to increase the temperature of the system becomes higher if the system is denser, with more particles to which heat must be transferred in a given volume.#

NJ: C_V is an *extensive* property.

Additionally, this quantity decreases with temperature for a given density. This is a more subtle characteristic and cannot easily be predicted from a classical treatment. Quantum mechanically, it could be thought to result from the convergence of energy levels. At higher temperatures, high energy levels are already occupied, and it becomes less energetically demanding to occupy yet higher energy levels. Heat can therefore be transferred more easily to the system.

STRUCTURAL PROPERTIES AND THE RADIAL DISTRIBUTION FUNCTION

TASK: perform simulations of the Lennard-Jones system in the three phases. When each is complete, download the trajectory and calculate $g(r)$ and $\int g(r)\mathrm{d}r$. Plot the RDFs for the three systems on the same axes, and attach a copy to your report. Discuss qualitatively the differences between the three RDFs, and what this tells you about the structure of the system in each phase. In the solid case, illustrate which lattice sites the first three peaks correspond to. What is the lattice spacing? What is the coordination number for each of the first three peaks?

Reasonable parameters to set for each state were determined from the phase diagram for the Lennard-Jones system:

Gas: Density = 0.05 Temperature = 1.2

Liquid: Density = 0.8 Temperature =1.2

Solid: Density = 1.2 Temperature = 1.2

The RDFs calculated from the trajectories for the three systems are represented below

Figure 14: RDFs for Solid, Liquid, and Gas states

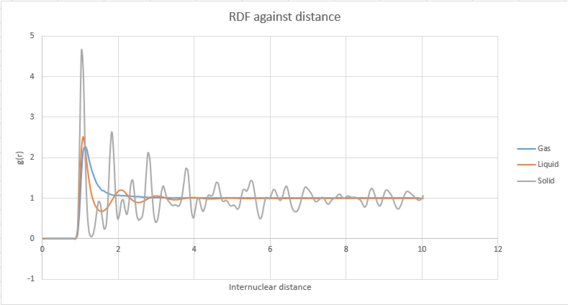
The radial distribution function takes for reference an arbitrarily chosen atom and indicates the density of neighbouring atoms as a function of internuclear distance. It is a good way to understand the relative arrangement of atoms in each different state.

For all cases, the RDF is equal to 0 for interatomic distances smaller than 0.9. This is due to the Lennard Jones repulsion term being high for very short distances which prevents any atom entering withing this range of the reference particle.

In the gas case, only one broad peak can be observed, around a distance of 1. This confirms the gas phase displays the smallest amount of order.

In the liquid case, three peaks with decreasing amplitudes can be observed at short distances. This shows liquids present some amount of order. This is due to interactions between atoms which though able to move are brought closer together and interact. The parallel can be drawn with solvation shells for solutes in water. The configuration directly around the reference atom is somewhat fixed whereas the rest of the surroundings can move freely in any direction.

File:Fcc lattice.PNG

Figure 15: Lattice Sites Corresponding to Peaks

In the solid case, peaks can be observed throughout the entire range of distances simulated. This is indicative of both short and long range order in the solid phase. The peaks, especially the first three, are also narrow and well-defined compared to what can be seen in the other cases. This is because the atoms in a solid are fixed and therefore coordination shells are found consistently at the same positions compared to the other cases which allow more movement and wider variation of the particle's positions. The peaks can therefore be directly related to a specific lattice sites in the face centered cubic lattice. The internuclear distances with these sites have been drawn in fig.15 with the number giving their order of appearance in the RDF. The shortest corresponds to the first peak or coordination sphere and the largest to the third peak.

This implies that the lattice spacing is given by the second peak which corresponds to a distance of 1.825.

File:RDFDissol.PNG

Figure 16: RDF Solid Case

Looking at these specific lattice sites on fig.15, the coordination number of the respective peaks can therefore be determined. It is equal to 12 for the first peak, 6 for the second peak, and 24 for the third peak.

NJ: You've mislablelled the peaks, unfortunately - the small one you ignored counts as a peak. Excellent otherwise.

DYNAMICAL PROPERTIES AND THE DIFFUSION CONSTANT

TASK: In the D subfolder, there is a file liq.in that will run a simulation at specified density and temperature to calculate the mean squared displacement and velocity autocorrelation function of your system. Run one of these simulations for a vapour, liquid, and solid. You have also been given some simulated data from much larger systems (approximately one million atoms). You will need these files later.

TASK: make a plot for each of your simulations (solid, liquid, and gas), showing the mean squared displacement (the "total" MSD) as a function of timestep. Are these as you would expect? Estimate $D$ in each case. Be careful with the units! Repeat this procedure for the MSD data that you were given from the one million atom simulations.

The mean square displacement results for each phase are given below in the respective figures. In the case of a gas, the MSD tends to increase linearly with time after a certain number of initial timesteps.

NJ: Well spotted, do you know why?

A better linear fit can therefore be found by looking at the values obtained after 2000 timesteps, after the system has equilibrated with the atoms moving randomly. This allows to calculate the diffusion coefficient for an equilibrated system with more accuracy. It is found using the formula:

$D=\frac{1}{6}\frac{d<r^2(t)>}{dt}$

The gradient found in timesteps units must be converted to time units.

As $\frac{d<r^2(t)>}{dt}$ has units of $\frac{MSD}{timesteps}$ and the timesteps used was equal to 0.002 time units, it must be divided by 0.002.

File:MSD Gas.PNG

Figure 17: Mean Square Displacements for the Gas Phase

The resulting diffusion coefficients are 3.03 and 3.02 for 1 million atoms.

File:MSD LiquidTB.PNG

Figure 18: Mean Square Displacements for the Liquid Phase

The liquid case presents a very clear linear trend. The mean squared displacement increases linearly with timestep as can be expected in a liquid where atoms move randomly through Brownian motion. From the gradient, the resulting diffusion coefficients calculated are $8.49\times 10^{-2}$ and $8.73\times 10^{-2}$ for 1 million atoms.

File:MSD SolidTB.PNG

Figure 19: Mean Square Displacements for the Solid Phase

The resulting estimated diffusion coefficients are $5.83\times 10^{-7}$ and $4.39\times 10^{-6}$ for 1 million atoms. The mean squared displacement equilibrates around an extremely small value and remains constant after as can be expected from a solid in which the atoms are fixed on specific lattice sites. More than these specific values, the fact that this is negligible compared to the other two cases can be retained.

It can also be concluded that the simulation with 1 million atoms does not bring much more information than the one with tens of thousands as the results are very consistent with the simulations run on these smaller boxes. It simply smoothens the trends observed. It is therefore not necessary to include so many atoms in the calculations especially as it is much more demanding in terms of computations.

TASK: In the theoretical section at the beginning, the equation for the evolution of the position of a 1D harmonic oscillator as a function of time was given. Using this, evaluate the normalised velocity autocorrelation function for a 1D harmonic oscillator (it is analytic!):

$C\left(\tau \right)=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}v\left(t\right)v(t+\tau )\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{v}^2\left(t\right)\mathrm{d}t}$

First, we can give an expression for the functions inside the integrals as we know how velocity depends on the position for a classical 1D harmonic oscillator.

The position $x(t)$ for a classical harmonic oscillator is given as seen in the Introduction section by:

$x=Acos(\omega t+\varphi )$

The velocity can be inferred:

$v(t)=\frac{dx}{dt}=-A\omega sin(\omega t+\varphi )$ as can be calculated by differentiating using the chain rule

With $t=t+\tau$:

$x=Acos[\omega (t+\tau )+\varphi ]$

and:

$v(t+\tau )=-A\omega sin(\omega t+\omega \tau +\varphi )$

This can now be inserted in the equation for $C\left(\tau \right)$:

$C\left(\tau \right)=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}v\left(t\right)v(t+\tau )\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{v}^2\left(t\right)\mathrm{d}t}$

Which gives:

$C(\tau )=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}A\omega sin(\omega t+\varphi )A\omega sin[\omega t+\omega \tau +\varphi ]\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}A\omega sin(\omega t+\varphi )A\omega sin(\omega t+\varphi )\mathrm{d}t}$

$C(\tau )=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}sin(\omega t+\varphi )sin[\omega t+\omega \tau +\varphi ]\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}si{n}^2(\omega t+\varphi )\mathrm{d}t}$

Using the trigonometric identity:

$sin(u+v)=sin(u)cos(v)+cos(u)sin(v)$

It can be expressed as follows:

$sin(\omega t+\omega \tau +\varphi )=sin(\omega t)cos(\omega \tau +\varphi )+cos(\omega t)sin(\omega \tau +\varphi )$

Giving:

$C(\tau )=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}sin(\omega t+\varphi )[sin(\omega \tau )cos(\omega t+\varphi )+cos(\omega \tau )sin(\omega t+\varphi )]\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}si{n}^2(\omega t+\varphi )\mathrm{d}t}$

$C(\tau )=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}sin(\omega t+\varphi )sin(\omega \tau )cos(\omega t+\varphi )+si{n}^2(\omega t+\varphi )cos(\omega \tau )\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}si{n}^2(\omega t+\varphi )\mathrm{d}t}$

$C(\tau )=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}sin(\omega t+\varphi )sin(\omega \tau )cos(\omega t+\varphi )\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}si{n}^2(\omega t+\varphi )\mathrm{d}t}+\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}si{n}^2(\omega t+\varphi )cos(\omega \tau )\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}si{n}^2(\omega t+\varphi )\mathrm{d}t}$

$C(\tau )=\frac{sin(\omega \tau )\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}sin(\omega t+\varphi )cos(\omega t+\varphi )\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}si{n}^2(\omega t+\varphi )\mathrm{d}t}+\frac{cos(\omega \tau )\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}si{n}^2(\omega t+\varphi )\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}si{n}^2(\omega t+\varphi )\mathrm{d}t}$

$C(\tau )=\frac{sin(\omega \tau )\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}sin(\omega t+\varphi )cos(\omega t+\varphi )\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}si{n}^2(\omega t+\varphi )\mathrm{d}t}+cos(\omega \tau )$

With the first term

$C(\tau )=\frac{sin(\omega \tau )\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}sin(\omega t+\varphi )cos(\omega t+\varphi )\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}si{n}^2(\omega t+\varphi )\mathrm{d}t}$

Equal to zero as

$\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}sin(x)cos(x)\mathrm{d}t=0$

Therefore

$C(\tau )=cos(\omega \tau )$

Be sure to show your working in your writeup. On the same graph, with x range 0 to 500, plot $C\left(\tau \right)$ with $\omega =1/2\pi$ and the VACFs from your liquid and solid simulations. What do the minima in the VACFs for the liquid and solid system represent? Discuss the origin of the differences between the liquid and solid VACFs. The harmonic oscillator VACF is very different to the Lennard Jones solid and liquid. Why is this? Attach a copy of your plot to your writeup.

The VACFs from the simulations can be compared to the harmonic oscillator VACF.

File:VACFScomp.PNG

Figure 20: Simulated VACFs compared to Harmonic Oscillator VACF

The minima in the VACFs for the liquid and solid system represent a change in the direction and of the atoms resulting from a collision. After this initial minimum, the behaviour differs between the VACF of the solid and that of the liquid. The VACF for the solid phase displays a decaying oscillation around the value of zero which is due to solids' higher degree of order whereas for the liquid it directly becomes constant and equal to zero as a reference atom only interacts with its direct surrounding (cf. RDFs).

NJ: Precisely - the negative regions of the VACF correspond to collision with other atoms. The single minimum in the liquid VACF is due to collision with the "solvent cage".

This is very different to the harmonic oscillator's behaviour for which no energy is lost through collisions which are considered to be elastical. Therefore its VACF shows a periodic oscillation around the value of 0.

NJ: There's nothing for the HO to collide with, so its velocity can never become decorrelated.

TASK: Use the trapezium rule to approximate the integral under the velocity autocorrelation function for the solid, liquid, and gas, and use these values to estimate $D$ in each case. You should make a plot of the running integral in each case. Are they as you expect? Repeat this procedure for the VACF data that you were given from the one million atom simulations. What do you think is the largest source of error in your estimates of D from the VACF?

From the VACF against time and by using the trapezium rule, it is possible to plot the running integral under the VACF as a function of time. The D value can be estimated from the final values of the running integrals which correspond to the plateau reached after a sufficient time has passed for the VACF to equilibrate around 0.

File:VACF Gas.PNG

Figure 21: VACFs and Running Integrals Gas

For a gas, the diffusion coefficient is estimated to be 3.29 for the simulation performed or 3.27 for 1 million atoms. With few interactions between the atoms and therefore slower loss of energy through collisions, the vapour phase has a characteristic running integral which reaches high values and takes longer to plateau compared to the other phases.

File:VACF Liquid.PNG

Figure 22: VACFs and Running Integrals Liquid

For a liquid, the diffusion coefficient is estimated to be $9.8\times 10^{-2}$ or $9.0\times 10^{-2}$ for 1 million atoms. The running integral equilibrates after the first and only significant minimum.

File:VACF Solid.PNG

Figure 23: VACFs and Running Integrals Solid

For a solid, the diffusion coefficient is estimated to be $3.6\times 10^{-5}$ or$4.6\times 10^{-5}$ for 1 million atoms. It is very small as could be expected from the fact that the VACF against timestep initially presents periodic oscillations around the x-axis which cancel each other out.

These diffusion coefficient values are consistent with the ones obtained using the mean squared displacement method. Extending the calculation to 1 million atoms proves unnecessary again. While the trends are smoothened, the results obtained with a smaller set of atoms are sufficiently accurate.

The use of the trapezium rule for integration can be thought to be a possible source of error in the final values obtained. Indeed, given that the VACFs are not periodic the error from the approximation adds up with time. More accurate mathematical integration methods could be used to refine the plot of the running integral.