Talk:Mod:Hunt Research Group/legendre

Investigation of reorientational dynamics in liquids using the Legendre reorientational time correlation functions.

The rotational motions in liquids are very sensitive on the local environment around the molecules and depend very much on the intermolecular interactions
between each rotating molecule and its surrounding molecules. Very often, in order to investigate the rotational dynamics in molecular liquids
and to provide a quantitative description of these relaxation processes we use the so-called “Legendre Reorientational Time Correlation functions”.
In general, the reorientational dynamics for specified intramolecular vectors are investigated by means of the Legendre reorientational tcfs:

(1)
In this equation u is a unit vector along a specified direction inside a molecule and P is a Legendre polynomial, e.g.:



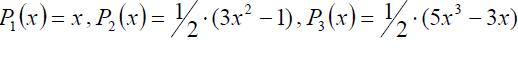
The corresponding reorientational times are defined as follows:

(2)

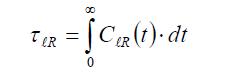
These quantities can be extracted by molecular dynamics simulations, as well as by experimental techniques such as infrared absorption,
dielectric relaxation, Raman and Rayleigh scattering, NMR relaxation as well as time resolved spectroscopy [1].
When investigating reorientational dynamics in liquids we have to take into account at least two extreme cases,
described by the corresponding theoretical models.
The first one is the Debye diffusion model [2], describing the molecular reorientation as an “infinitely small”
step angular random walk (angular Brownian motion).This model is often used to describe reorientation mechanisms in “liquid-like” dense fluids.
The other one, which is frequently applied to analyze reorientational dynamics in low-density “gas-like” fluids,
is called the inertial rotation or free rotor model, according to which the molecules can rotate freely during
a period perturbed by molecular collisions.
In the case of diffusive (Debye) reorientational dynamics, the Legendre reorientational correlation functions exhibit
single exponential time decay. The time constant of this exponential decay is the Legendre reorientational correlation time:
(3)

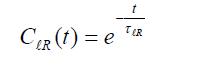
In this case the first, second and third order Legendre reorientational times are related through the equations:
(4)

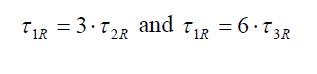
Furthermore, according to the diffusive model the Legendre reorientational times are related to the rotational diffusion
coefficient through the equation:
(5)

Other theoretical models like e.g. the extended J-diffusion model [3] have been also proposed in the literature
to interpret the reorientational dynamic behaviour of several molecular liquid systems.
In the case of strongly hydrogen bonded molecules (e.g. liquid water) the reorientational dynamics cannot
be interpreted by using a diffusive Debye model and a newly presented Extended Jump model has been recently proposed [4].
According to this model, water reorientation proceeds mainly via large angular jumps occurring during an exchange of H-bond
acceptors plus a slower, less important, component related to the H-bond axis diffusive reorientation.

Effect of the local HB network on reorientational dynamics.

In order to depict more clearly the significance of the strength of the intermolecular interactions and of the
local structural network on the reorientational dynamics in hydrogen bonded fluids, we performed an additional analysis
of reorientational dynamics, where we calculated the Legendre reorientational tcfs as a function of the hydrogen bonds per
molecule. These functions can be defined as follows [5]:
... etc (6)
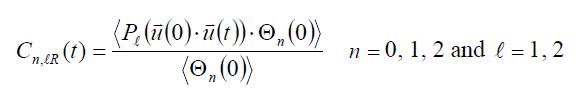
As previously, the index l defines the order of the Legendre polynomial, whereas the index n defines the
instantaneous number of hydrogen bonds which forms a molecule at each time t.
The function is defined as follows:
, if a molecule forms n hydrogen bonds at time t.
, otherwise.
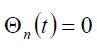
The corresponding reorientational times are defined as:
(7)

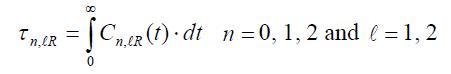
References

1)(a) Spectroscopy and Relaxation of Molecular Liquids; Steele, D., Yarwood, J., Eds.; Elsevier: Amsterdam, 1991 

  (b) Vibrational Spectra and Structure; Durig, J. R., Ed.; Elsevier: Amsterdam, 1977; Vol. 6 

  (c) Steele, W. A. Adv. Chem. Phys. 1977, 34, 1
2) Debye, P. Polar Molecules; Dover: New York, 1945
3) Gordon, R. G. J. Chem. Phys. 1966, 44, 1830
4) Laage, D.; Hynes,J. T. J. Phys. Chem. B 2008, 112, 14230
5) Skarmoutsos, I.; Guardia, E. J. Phys. Chem. B 2009, 113, 8898