Talk:Mod:Hunt Research Group/ion pair scan
How to... conduct a systematic conformational analysis for an ion pair dimer
|
This is a tutorial about a simple procedure to spherical scan of the potential energy surface of one molecule sampled by another molecule used as a probe. For this scan would be convenient to have a referiment atom in the centre of the sphere but not often the centre of the sphere is occupied by an atom and Gaussian do not allow us to use dummy atoms as referiments for relaxed angle scan (keyword: modredundant). To do that we have to define a coordinate system with some dummy atoms and operate a Z-matrix scan on the coordinates by using the keyword opt=z-matrix in the route. Herein, I’ll show step by step what I’ve done to set the PES scan for the [C1C4Im][C2C2DTC] ion pair. |
1 - Set the referiment system of your scan
As first step you’ll introduce these four dummy atoms reported below as the first four atoms of your z-matrix.
0 1 X X 1 3.00000000 X 1 3.00000000 2 A1 X 1 3.00000000 2 90.00000000 3 D1 0
These atoms are set to allow us to rotate X3 and X4 in 2 perpendicular planes by modifying A1 and D1 variables.
2 – Define your molecules
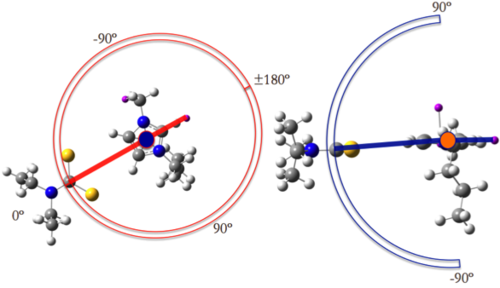
Now we have to define the molecules involved in the scan. Each molecule has to be self-referred. This means that its atoms are referred to atoms inside the same molecule so that when one of the atom coordinates is altered all the other atoms referred to it follows that atom; Notwithstanding, the first three atoms declared are an exception as they has to be referred to atoms external to the molecule. To obtain uniquely the rotation of the molecule around the other these three atoms were referred to a set of dummy atoms. To execute a 2D rotational scan 4 dummy atoms has been used. Two of them are static trough the scan whereas the other two rotates around the two static ones. Thinking thoughtfully to the system can be understood why 4 atoms are used. To define a point in the space by a Z-matrix you define it in relation to other points previously defined. Three parameters are used to define a point in the space : the interatomic distance, the angle, and the dihedral angle. The first two parameters can be defined respectively to the two static dummy atoms. Because the rotation of the other two atoms is in plane with the two static dummy atoms it does not affect a dihedral angle defined by the use of rotating atom as one of the terminal atoms of the dihedral angle.
This is the hard point of the creation of the .com file because you have to set the coordinates of the first three atoms thoughtfully to allow the rotation of the molecule without affecting the coordinates of these atoms during it. This can be checked by rotating the angle in gaussview and seeing if the result is what expected. Hopefully, the procedure described hereafter should work but I do not have occasion to check it onto molecules other than the one displayed.
In order to proceed, we have to distinguish the role of the 2 molecules, one will be our ‘probe’ and the other will be our ‘sample’. The ‘sample’ will rotate on itself whereas the ‘probe’ will move around the ‘sample’. The two molecules will respectively move in 2 perpendicular planes of rotation, which will allow to carry out the spheric scan of the interactions between the two molecules.
The dummy atoms 1 and 2 must be included in the axis of rotation of the ‘sample’ and 1 will be the ‘centre of inversion’ of the sphere.
The first three atoms of the probe must be set like this :
C 1 B1 3 178.99999509 2 -72.98467412 0 S 30 1.72416943 1 58.52894245 2 D2 0 S 30 1.72774347 31 122.85100226 1 1.94989600 0
The first atom (atom 30 in this case) is set so that the sample-probe distance is determined by the variable B1, then the angle defines that the atom will be positioned approximatively in line with the atom 1 and 3 so that moving 3 will inherently move this atom and the dihedral angle defines the plane perpendicular to the 1 2 3 atoms plane where the atom 30 will lay(notice that the plane containing 1 2 3 will change through the scan with the movement of the atom 3).
The second atom (atom 31 in this case) is defined with respect to the previous atom for the interatomic distance. Because 1 is the center of the system the angle 1 30 31 will be constant therefore is a good way to define the atom 31 position. Dihedral angle is defined but left variable so that the molecule can tilt respect to the 30-1 axis. The atom 2 is not modified through the scan so it is a good place holder to be used to define the dihedral angle and the variation of the 30 atom position with respect to the movement of the atom 3 does not affect the 31 30 1 2 dihedral angle because it doesn't vary the plane defined by the atoms 30 1 2.
The third atom is defined for the interatomic distance and the angle with respect of the two other atoms defined before. The dihedral angle is defined with respect of the atom 1 that being the centre of the system does not make the dihedral angle trough the scan (plane defined by 30 31 and 1 does not vary trough the scan)
All the remaining atoms of the molecule are defined with respect to these three atoms defined here so that when these three atoms move all the molecule moves coherently. THis can be imposed by the button in gaussview with the letter 'A' that allows to change the coordinates.
The first three atoms of the sample molecule are defined as it follows :
C 1 1.15771466 2 90.00000000 4 90.00000000 0 N 1 1.17242544 5 71.45544166 2 83.48309458 0 N 1 1.13616026 5 69.80539566 6 -173.48309458 0
The position of the molecule is fixed but the first of the three atoms defines the dihedral angle with respect of the coordinates of the atoms C(5) 1 2 4 therefore the rotation of the dummy atom 4 will result in the inherent rotation of the C atom (the dihedral angle that defines the position of the atom 4 is a variable). The other two atoms are defined with the atoms 1 and 2 that does not move during the scan.
3 – Set the scan
After the z-matrix a white line must be left and then we will set our variables :
B1 5.86611814 A1 90.00000000 S 9 -9.90000 D1 -90.00000000 S 9 +10.00000 D2 -90.00000000
Obviously your values will be different but the scan amongst the angle A1 should rotate the probe over and under the plane formed by the atoms 1,3,4 and D1 should rotate the probe in the plane formed by 1,2,3. It is important to remember that Gaussian has some issues with the limiting angles therefore is better to scan until ~179 or ~1 to avoid script faults. Remember to set the opt=z-matrix in the script route.
%nprocshared=8 %mem=14400MB %chk=test_IN_ON_90.chk # opt=z-matrix b3lyp/6-31g nosymm geom=connectivity empiricaldispersion=gd3 BMIM 0 1 X X 1 2.00000000 X 1 3.00000000 2 A1 X 1 3.00000000 2 90.00000000 3 D1 0 C 1 1.15771466 2 90.00000000 4 90.00000000 0 N 1 1.17242544 5 71.45544166 2 83.48309458 0 N 1 1.13616026 5 69.80539566 6 -173.48309458 0 C 6 2.20589881 7 36.75204317 5 179.62354220 0 C 7 2.20741318 6 36.76548810 5 -179.76966396 0 H 8 3.24571830 6 41.19810842 7 -0.35958291 0 C 6 1.47006172 5 126.67015792 7 179.44651575 0 C 7 1.48214358 6 161.27267589 8 170.17035599 0 H 8 1.07651940 6 167.56517796 7 179.25571448 0 H 9 1.07678623 6 122.06766763 7 179.41091048 0 H 11 1.08952723 6 109.31735900 7 121.89721467 0 H 11 1.08956200 6 109.42948493 7 -117.41092715 0 H 11 1.08825013 6 109.03687137 7 2.28983614 0 C 12 1.53044333 6 112.70900607 7 88.75485300 0 H 12 1.09089731 6 115.47545821 7 -41.55756898 0 H 12 1.09150376 6 96.58931706 7 -154.92737321 0 C 18 1.53159261 12 114.02466815 7 60.21093562 0 H 18 1.09474130 12 106.71484623 7 -178.13510738 0 H 18 1.09574182 12 109.46847196 7 -63.61295391 0 C 21 1.53133717 18 112.36924430 12 177.24888774 0 H 21 1.09703026 18 109.68946719 12 -61.12025577 0 H 21 1.09729776 18 109.24326164 12 55.39969468 0 H 24 1.09178867 21 111.10805048 18 179.79823172 0 H 24 1.09323755 21 111.08215903 18 -60.23501784 0 H 24 1.09375708 21 111.13297855 18 59.78378948 0 C 1 B1 3 178.99999509 2 -72.98467412 0 S 30 1.72416943 1 58.52894245 2 D2 0 S 30 1.72774347 31 122.85100226 1 1.94989600 0 N 30 1.38649628 31 118.69787900 32 179.88857349 0 C 33 1.46198199 30 122.51211282 32 176.69344464 0 C 33 1.46194880 30 122.67895299 34 -179.91918915 0 H 34 1.09727882 33 107.79539191 30 -147.02448390 0 H 34 1.08972480 33 108.19170344 30 -30.07257517 0 C 34 1.53221816 33 112.70644243 30 91.09689577 0 H 35 1.09729025 33 107.78009396 30 -147.24569440 0 H 35 1.08967434 33 108.19965873 30 -30.30969788 0 C 35 1.53224904 33 112.72406370 30 90.88083173 0 H 38 1.09170104 34 108.92193675 33 -62.10201645 0 H 38 1.09523444 34 111.32513550 33 57.95875345 0 H 38 1.09666295 34 110.72033274 33 178.37187932 0 H 41 1.09519819 35 111.31213651 33 57.80156920 0 H 41 1.09171890 35 108.94832172 33 -62.26011562 0 H 41 1.09664056 35 110.70985861 33 178.21143471 0 B1 5.86611814 A1 90.00000000 S 9 -9.90000 D1 90.00000000 S 9 -10.00000 D2 -90.00000000 1 2 1.5 3 2.0 6 1.0 2 5 1.0 7 1.0 3 4 1.5 8 1.0 4 5 2.0 9 1.0 5 10 1.0 6 7 11 1.0 12 1.0 13 1.0 8 14 1.0 15 1.0 16 1.0 9 10 11 12 13 14 17 1.0 18 1.0 19 1.0 15 16 17 20 1.0 21 1.0 22 1.0 18 19 20 23 1.0 24 1.0 25 1.0 21 22 23 24 25 26 27 1.0 28 1.0 29 1.0 27 28 29 30 1.0 31 1.0 30 32 1.0 33 1.0 34 1.0 31 35 1.0 36 1.0 37 1.0 32 33 34 38 1.0 39 1.0 40 1.0 35 36 37 41 1.0 42 1.0 43 1.0 38 39 40 41 42 43
4 – What can go wrong
Personally, I suggest to do multiple ‘little’ scans because in the scan fails the output will not be formatted by gaussview as a X, Y, Z table that is useful for further elaboration. For example, I have done eight scans but two have failed because the butyl chain causes to the script to do not converge. In my case I have tried to add the keyword in the route INT=ultrafine opt=(z-matrix, tight, maxcycles=250) but this does not solve my problem. I have tried to reduce the freedom of the molecule fixing the D2 angle but also that does not deserve to anything. The solution has been to unfreeze the butyl chain. A similar issue can happen also to you and for me the solution has been more conformational freedom, carefully given where needed.
5 – Further elaboration
After gain your data you have to plot them in a graph. Matlab is a big, heavy and powerful suite of mathematical elaboration scripts that is really useful to produce automatized procedures to output your data as a surface plot by the command surf(). If you would like to try to use this software suite I have added a an help page that should help you to plot your scans output.(link available soon) Otherwise you can use a simple plotting software but I think that matlab allows you to have a workspace extremely useful. For example it can produce derivatives of your data spotting out the minimum and maximum of your data.