Talk:Mod2:mathieu08
Module 3
https://www.ch.imperial.ac.uk/wiki/index.php?title=Talk:Mod2:mathieu08&action=edit§ion=1
This tutorial examines the Cope rearrangement of 1,5-hexadiene and uses it as an example of how to study the chemical reactivity of a reaction through transition structure analysis. The Cope rearrangement is illustrated in the diagram below:
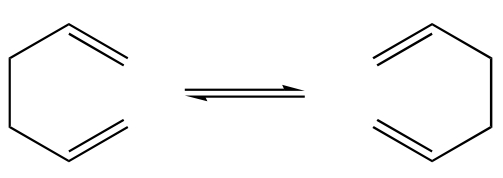
This reaction is an example of a [3,3]-sigmatropic shift rearrangement and has been the centre of much deliberation, primarily as to whether the mechanism it proceeds by occurs in a concerted, stepwise or dissociative manner. It is currently accepted that the reaction proceeds in a concerted fashion via either a "chair" or a higher energy "boat" transition structure. The techniques used to model this computationally are exercised in this tutorial and the results are illustrated in the following section.
Optimisation: HF method/3-21g basis set
Total energy from the 1st optimisation of anti hexadiene was: -231.69260236 a.u.
The Point group of the anti conformer was - C2
This is the anti1 conformer from comparison of the energy and point group with the data in the appendix 1 table.
Anti1 1,5-hexadiene
- [ ASK ABOUT BACKGROUND COLOUR CODE AND BUTTON CODE]
The gauche conformer is expected to have a higher total energy than the anti conformer as it appears to have more steric interaction upon brief observation of the two molecules.
The total energy from the optimised gauche hexadiene was: -231.69266120 a.u.
This value is marginally smaller than that obtained for the anti structure. This observation is opposite to what was expected insomuch that there is less steric repulsion in the gauche structure giving it a lower total energy.
Point group - C1
Comparison of the total energy and the point group with the data in the appendix 1 table elucidates that this is the gauche3 conformer.
Gauche3 1,5-hexadiene
It was believed that the anti C2 conformer would still give the most stable conformation with lowest energy despite the earlier gauche conformer giving a more stable molecule than the initially calculated anti1 conformer.
The anti conformer proposed was the anti2 conformer from the appendix table with Total Energy: -231.69253528 a.u. This energy matches that provided in the table for the anti2 conformer to 5 decimal places in accuracy.
The point group of this structure was Ci, also in accord with the data in the table for the anti2 conformer.
anti2 (table data)
Point group: Ci, Total Energy: -231.69254
Anti2 1,5-hexadiene
Observation of the table at the bottom of the instruction page shows that the C1 gauche conformer is in fact the most stable hexadiene structure. This can be explained due to the 1,4 stabilising hydrogen attractions (gecko effect) . Incidentally the first structure obtained for the gauche conformation is the most stable gauche3 conformer.
Comparison of the energy of the above anti Ci conformer with the value form the table for the same conformer shows that the energies match perfectly.
anti2 (table data)
Point group: Ci, Total Energy: -231.69254, 0.08
The energy of the DFT/B3LYP 6-31g basis set optimised anti2 was found to be: E(RB3LYP) -234.55970424 a.u., lower therefore more stable than that of the optimised structure using the 3-21g basis set.
Difference in geometry between 3-21g basis set and 6-31g: 3-21g: 4 central atoms dihedral = 179.995 end alkenes: 124.808 & 124.810 4 left atoms (dihedral): -114.698 4 right atoms (dihedral): 114.673
6-31g: 4 central atoms dihedral = 180.00 and alkenes: 125.208 & 125.208 4 left atoms (dihedral): -118.776 4 right atoms (dihedral): 118.775
| 3-21g optimisation
|
6-31g optimisation
|
Frequency analysis:
low frequency data: Low frequencies --- -9.3645 0.0006 0.0006 0.0007 3.6221 13.1700 Low frequencies --- 71.9003 79.9172 116.8581
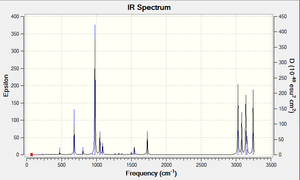
Thermochemistry: the desired energies are provided below -
[Coreections]
[0 K] Sum of electronic and zero-point Energies= -234.416244
[298.15 K & 1 atm] Sum of electronic and thermal Energies= -234.408954
[RT(H= E + RT)] Sum of electronic and thermal Enthalpies= -234.408010
[(G=H-TS)] Sum of electronic and thermal Free Energies= -234.447849
The first of these is the potential energy at 0 K including the zero-point vibrational energy (E = Eelec + ZPE), the second is the energy at 298.15 K and 1 atm of pressure which includes contributions from the translational, rotational, and vibrational energy modes at this temperature (E = E + Evib + Erot + Etrans), the third contains an additional correction for RT (H = E + RT) which is particularly important when looking at dissociation reactions, and the last includes the entropic contribution to the free energy (G = H - TS).
Optimising the "chair" and "boat" transition structures
This section involves setting up a transition state structure optimisation, achieved by computing the force constants at the beginning of the calculation, using the redundant coordinate editor, and QST2. The reaction coordinate will be visualized and the IRC will be run to calculate the activation energies for the Cope rearrangement via the "chair" and "boat" transition states.
The structure of the allyl was produced in gaussview and optimised using the HF/3-21G level of theory, the result is illustrated below:
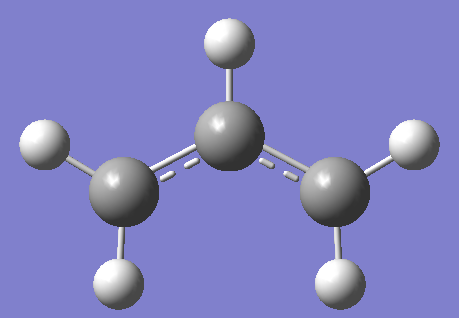
This structure was dubplicated and the bond separation between the terminal carbons was set to 2.2 Angstroms to give the chair conformer of the transition state with C2h symmetry.
Having created the chair conformer of the transition state it will now be optimised manually via two different procedures which are demonstrated in the ensuing section:
We are now going to optimize this transition state manually in two different ways. Transition state optimizations are more difficult than minimizations because the calculation needs to know where the negative direction of curvature (i.e. the reaction coordinate) is. If you have a reasonable guess for your transition structure geometry, then normally the easiest way to produce this information is to compute the force constant matrix (also known as the Hessian) in the first step of the optimization which will then be updated as the optimization proceeds. This is what we will try to do in the next section. However, if the guess structure for the transition structure is far from the exact structure, then this approach may not work as the curvature of the surface may be significantly different at points far removed from the transition structure. In some cases, a better transition structure can be generated by freezing the reaction coordinate (using Opt=ModRedundant and minimizing the rest of the molecule. Once the molecule is fully relaxed, the reaction coordinate can then be unfrozen and the transition state optimization is started again. One advantage of doing this, is that it may not be necessary to compute the whole Hessian once this has been done, and just differentiating along the reaction coordinate might give a good enough guess for the initial force constant matrix. This can save a considerable amount of time in cases where the force constant calculation is expensive.
File:M3 TSberny chair TS -818 movieMF.mng
The vibration shown is that with a frequency of -818 cm-1 and can be seen to simulate the cope rearrangement, whereby the terminal carbons move towards and away from one another simultaneously at opposite ends of the transition state.
The energy of the TS Berny optimised structure was found to equal -231.619322 Hartree with C2h symmetry.
The alternative freeze coordinate method for optimising the transition state is displayed below:
An incorrect transition state was produced upon the second optimisation which is illustrated in the thumbnail alongside. This issue was remedied by altering the opimisation from a minimum to a transition state, TS berny to be precise. The correct final optimised structure of the chair transition state was derived via the freeze coordinate method and is displayed below:
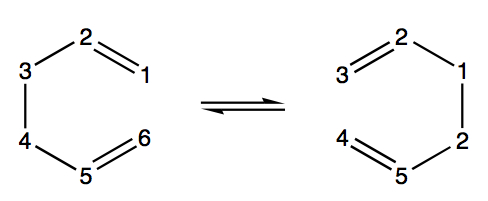
A different approach must be adopted to determine the optimised boat transition structure. Using the QST2 method, the calculation interpolates between two structures, in this case the reactant and the product to try and find the transition sate between them. To ensure this procedure works, one must make sure that the reactant and product are numbered in the same way, especially as both reactant and product are 1,5-hexadiene; the numbering as shown in the diagram below is changed manually.
As expected, the QST2 calculation fails because it is unable to realise that the top allyl fragment can be rotated, therefore simply producing what appears to look like a more dissociated form of the chair transition structure. It is evident that this method will continue to fail to locate the boat transition structure from these reactant and product structures.
To assist the QST2 calculation, the structures of the reactant and the product must be altered to better simulate the boat transition state structure. This was done manually by re numbering the atoms in the two chains and altering the dihedral angles of the central 4 carbon atoms to zero degrees (i.e. C2-C3-C4-C5 = 0o). The inside C-C-C were then selected (i.e. C2-C3-C4 and C3-C4-C5) and the angle reduced to 100o to give the following two structures:
| Reactant | Product |
Check Imaginary frequency, illustrate frequency HERE: