Talk:LiquidSimsJEF15

Overall: Pretty good - everything is there and most things are explained well. Just a comment on your writing style (and we will print these off for you to discuss), needs a bit of improvement before your project. Ensure that you establish the niche and talk about why the reader should be interested. Method should be very structured and easy to read. Results+discussion - make sure you're going to point B from point A without explaining how you get there. Conclusion, not a bad structure. Don't write for writing sake - your future work "we can compare with experimental data" isn't that futuristic! Mark: 66/100

Tasks

TASK: Open the file HO.xls. In it, the velocity-Verlet algorithm is used to model the behaviour of a classical harmonic oscillator. Complete the three columns "ANALYTICAL", "ERROR", and "ENERGY": "ANALYTICAL" should contain the value of the classical solution for the position at time $t$, "ERROR" should contain the absolute difference between "ANALYTICAL" and the velocity-Verlet solution (i.e. ERROR should always be positive -- make sure you leave the half step rows blank!), and "ENERGY" should contain the total energy of the oscillator for the velocity-Verlet solution. Remember that the position of a classical harmonic oscillator is given by $x\left(t\right)=A\cos (\omega t+\varphi )$ (the values of $A$, $\omega$, and $\varphi$ are worked out for you in the sheet).

File:Jef15HO.xls

TASK: For the default timestep value, 0.1, estimate the positions of the maxima in the ERROR column as a function of time. Make a plot showing these values as a function of time, and fit an appropriate function to the data.

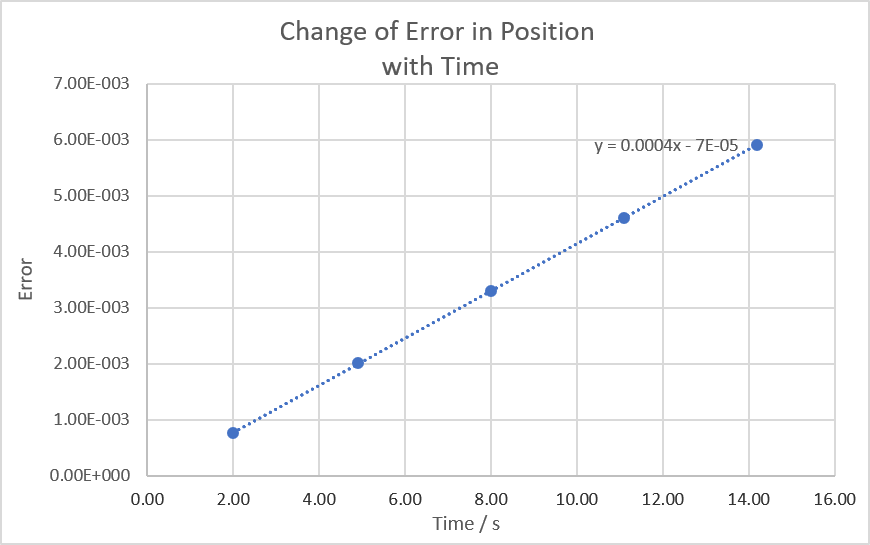Would have been nice for this to be plotted superposed on the original graph but good

TASK: Experiment with different values of the timestep. What sort of a timestep do you need to use to ensure that the total energy does not change by more than 1% over the course of your "simulation"? Why do you think it is important to monitor the total energy of a physical system when modelling its behaviour numerically?

A timestep of more than roughly 0.2 results in a change in total energy of more than 1% over the whole simulation. A smaller timestep (0.1) gives a more accurate result since the energy does not change by much more than 0.2% Tick

TASK: For a single Lennard-Jones interaction, $\varphi \left(r\right)=4ϵ(\frac{{\sigma }^{12}}{r^{12}}-\frac{{\sigma }^6}{r^6})$, find the separation, $r_0$, at which the potential energy is zero. What is the force at this separation? Find the equilibrium separation, $r_{eq}$, and work out the well depth ($\varphi \left(r_{eq}\right)$). Evaluate the integrals $\underset{2\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)\mathrm{d}r$, $\underset{2.5\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)\mathrm{d}r$, and $\underset{3\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)\mathrm{d}r$ when $\sigma =ϵ=1.0$.Tick

Potential energy is zero when r = σ. The force at this separation is 24ε/σ. Equilibrium separation can be calculated by equating the force (derivative of potential) to zero and is given by $\sigma \sqrt[6]{2}$, resulting in a well depth of ε (equilibrium energy is -ε).

$\underset{2\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)\mathrm{d}r=-0.0248$Tick

$\underset{2.5\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)\mathrm{d}r=-0.00818$Tick

$\underset{3\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)\mathrm{d}r=-0.00329$Tick

TASK: Estimate the number of water molecules in 1ml of water under standard conditions. Estimate the volume of 10000 water molecules under standard conditions.

1ml of water weighs 1g. Therefore in 1ml there is $\frac{1}{18}$ moles, there are $\frac{N_A}{18}=3.345\times 10^{22}$ molecules. The volume of a water molecule is roughly $\frac{1}{3.345\times 10^{22}}$ ml, so the volume of 10000 will be $\frac{1}{3.345\times 10^{18}}$ ml = $2.99\times 10^{-19}$ ml.Tick

TASK: Consider an atom at position (0.5,0.5,0.5) in a cubic simulation box which runs from (0,0,0) to (1,1,1). In a single timestep, it moves along the vector (0.7,0.6,0.2). At what point does it end up, after the periodic boundary conditions have been applied?.

(0.2,0.1,0.7)Tick

TASK: The Lennard-Jones parameters for argon are σ=0.34 nm, $\frac{ϵ}{k_B}=120K$. If the LJ cutoff is r*=3.2, what is it in real units? What is the well depth in kJmol^-1? What is the reduced temperature T*=1.5 in real units?

$r=1.088nm,ϵ=0.997kJmo{l}^{-1},T=180K$Tick

TASK: Why do you think giving atoms random starting coordinates causes problems in simulations? Hint: what happens if two atoms happen to be generated close together?

If the atoms are positioned randomly then two (or more) atoms may be generated very close together. This will cause the system to start in a position of high energy and cause a raised temperature.

TASK: Satisfy yourself that this lattice spacing (1.07722) corresponds to a number density of lattice points of 0.8. Consider instead a face-centred cubic lattice with a lattice point number density of 1.2. What is the side length of the cubic unit cell?

$\rho =\frac{N}{V}=\frac{N}{l^3}$

$l=\sqrt[3]{\frac{N}{\rho }}$

$\sqrt[3]{\frac{1}{0.8}}=1.07722$Tick

There are 4 atoms in the FCC lattice.

$\sqrt[3]{\frac{4}{1.2}}=1.4938$Tick

TASK: Consider again the face-centred cubic lattice from the previous task. How many atoms would be created by the create_atoms command if you had defined that lattice instead?

There are 4 atoms in an FCC lattice as opposed to 1. $4\times 10\times 10\times 10=4000$Tick

TASK: Using the LAMMPS manual, find the purpose of the following commands in the input script:

mass 1 1.0
pair_style lj/cut 3.0
pair_coeff * * 1.0 1.0

The first line sets the mass of atom type 1 to 1.0. The second one defines the type of interactions in play - Lennard-Jones with cutoff r=3σ. The third sets the coefficients ε=1 and σ=1.Tick, good

TASK: Given that we are specifying ${\mathbf{x}}_i\left(0\right)$ and ${\mathbf{v}}_i\left(0\right)$, which integration algorithm are we going to use?

Velocity-Verlet

TASK: Look at the lines below.

### SPECIFY TIMESTEP ###
variable timestep equal 0.001
variable n_steps equal floor(100/${timestep})
timestep ${timestep}

### RUN SIMULATION ###
run ${n_steps}

The second line (starting "variable timestep...") tells LAMMPS that if it encounters the text ${timestep} on a subsequent line, it should replace it by the value given. In this case, the value ${timestep} is always replaced by 0.001. In light of this, what do you think the purpose of these lines is? Why not just write:

timestep 0.001
run 100000

Ask the demonstrator if you need help.

Setting variables means that you can easily modify the code by changing either the time or the timestep and the number of steps run will be calculated automatically, rather than the alternative in which you have to manually recalculate each time you modify the code.Tick

TASK: make plots of the energy, temperature, and pressure, against time for the 0.001 timestep experiment (attach a picture to your report). Does the simulation reach equilibrium? How long does this take? When you have done this, make a single plot which shows the energy versus time for all of the timesteps (again, attach a picture to your report). Choosing a timestep is a balancing act: the shorter the timestep, the more accurately the results of your simulation will reflect the physical reality; short timesteps, however, mean that the same number of simulation steps cover a shorter amount of actual time, and this is very unhelpful if the process you want to study requires observation over a long time. Of the five timesteps that you used, which is the largest to give acceptable results? Which one of the five is a particularly bad choice? Why?

Equilibirum is reached for 0.001 timestep - all of the quantities plateau at a constant value. 0.0025 was the best timestep used, which gave very similar results to the 0.001 timestep but is a lot quicker to run. 0.015 timestep was particularly bad as its energy did not converge. Tick

TASK: Choose 5 temperatures (above the critical temperature T*=1.5), and two pressures (you can get a good idea of what a reasonable pressure is in Lennard-Jones units by looking at the average pressure of your simulations from the last section). This gives ten phase points — five temperatures at each pressure. Create 10 copies of npt.in, and modify each to run a simulation at one of your chosen points. You should be able to use the results of the previous section to choose a timestep. Submit these ten jobs to the HPC portal. While you wait for them to finish, you should read the next section.

TASK: We need to choose $\gamma$ so that the temperature is correct $T=\mathfrak{𝔗}$ if we multiply every velocity $\gamma$. We can write two equations:

$\frac{1}{2}\sum _i{m}_i{v}_i^2=\frac{3}{2}N{k}_{B}T$

$\frac{1}{2}\sum _i{m}_i{\left(\gamma v_i\right)}^2=\frac{3}{2}N{k}_B\mathfrak{𝔗}$

Solve these to determine $\gamma$.

$\gamma =\sqrt{\frac{T}{\mathfrak{𝔗}}}$Tick

TASK: Use the manual page to find out the importance of the three numbers 100 1000 100000. How often will values of the temperature, etc., be sampled for the average? How many measurements contribute to the average? Looking to the following line, how much time will you simulate? ????

Nevery = use input values every this many timesteps - 100, this controls how often averages are taken so an average is taken every 100 timesteps Nrepeat = # of times to use input values for calculating averages - 1000, this controls how many times averages are calculated Nfreq = calculate averages every this many timesteps - 100000, this controls when an overall average is calculated.Tick, good

TASK: When your simulations have finished, download the log files as before. At the end of the log file, LAMMPS will output the values and errors for the pressure, temperature, and density $\left(\frac{N}{V}\right)$. Use software of your choice to plot the density as a function of temperature for both of the pressures that you simulated. Your graph(s) should include error bars in both the x and y directions. You should also include a line corresponding to the density predicted by the ideal gas law at that pressure. Is your simulated density lower or higher? Justify this. Does the discrepancy increase or decrease with pressure?

The simulated density is lower than the ideal gas law. This is due to Lennard-Jones repulsions in the simulated gases causing the particles to spread out. In an ideal gas there are now such forces so the particles can coexist closer together. The discrepancy increases as pressure increases because the at an increased gram pressure there are a higher fraction of particles are experiencing attractive Lennard-Jones forces whereas the ideal gas law does not model these. The discrepancy also decreases as temperature increases because the Lennard-Jones forces become less significant compared to the thermal energy.Tick, nice

TASK: As in the last section, you need to run simulations at ten phase points. In this section, we will be in density-temperature $({\rho }^{*},T^{*})$ phase space, rather than pressure-temperature phase space. The two densities required at $0.2$ and $0.8$, and the temperature range is $2.0,2.2,2.4,2.6,2.8$. Plot $C_V/V$ as a function of temperature, where $V$ is the volume of the simulation cell, for both of your densities (on the same graph). Is the trend the one you would expect? Attach an example of one of your input scripts to your report.

Heat capacities are lower for lower density, this is because at higher densities the particles are closer together so heat can be transmitted between particles more effectively. As temperature increases, energy increases. At higher energies, the energy levels get closer together which means that exciting electrons to higher energy levels becomes comparatively easier.

FCC Lattice

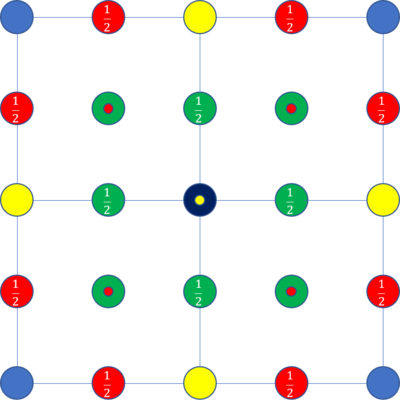
TASK: perform simulations of the Lennard-Jones system in the three phases. When each is complete, download the trajectory and calculate $g(r)$ and $\int g(r)\mathrm{d}r$. Plot the RDFs for the three systems on the same axes, and attach a copy to your report. Discuss qualitatively the differences between the three RDFs, and what this tells you about the structure of the system in each phase. In the solid case, illustrate which lattice sites the first three peaks correspond to. What is the lattice spacing? What is the coordination number for each of the first three peaks?

The gas RDF shows a single peak which converges to 1. The liquid RDF shows a similar pattern but oscillates around 1 before converging. The solid RDF shows many peaks which slowly decrease in size. Using the running integral, we can see that the first lattice site holds 12 atoms, the second lattice site holds 6 atoms and the third holds 24 atoms. specify the phase...If the dark blue atom denotes the atom around which we are studying, the lattice sites displayed in green are the first lattice site, remembering there are atoms at height $\frac{1}{2}$ and $-\frac{1}{2}$ resulting in 12 atoms in that site. The second site is denoted in yellow, there are also atoms 1 lattice spacing above and 1 below (small yellow dot), giving 6 atoms. The third lattice site is shown in red, there are atoms at height $\frac{1}{2}$ and height $-\frac{1}{2}$ as well as the 4 atoms at height 1 above and 4 at height 1 below the central atoms (small red dots) giving 24 atoms. The lattice spacing can be calculated from the density (1.2 in this case) which results in a lattice spacing of 1.494. This is confirmed by the location of the peaks. The peaks are calculated to be at 1.056, 1.494 and 1.830 from the central atom. This is observed in the RDF.Tick

TASK: In the D subfolder, there is a file liq.in that will run a simulation at specified density and temperature to calculate the mean squared displacement and velocity autocorrelation function of your system. Run one of these simulations for a vapour, liquid, and solid. You have also been given some simulated data from much larger systems (approximately one million atoms). You will need these files later.

TASK: make a plot for each of your simulations (solid, liquid, and gas), showing the mean squared displacement (the "total" MSD) as a function of timestep. Are these as you would expect? Estimate D in each case. Be careful with the units! Repeat this procedure for the MSD data that you were given from the one million atom simulations.

The "total" MSD increases rapidly for gases to a very large value (compared to liquid or solid). This is expected since the particles in a gas have much more freedom and so have the greatest displacement. The liquid molecules have a smaller MSD but still move around. The solid molecules do not have any freedom and so have a very small MSD.Tick

TASK: In the theoretical section at the beginning, the equation for the evolution of the position of a 1D harmonic oscillator as a function of time was given. Using this, evaluate the normalised velocity autocorrelation function for a 1D harmonic oscillator (it is analytic!):

$C\left(\tau \right)=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}v\left(t\right)v(t+\tau )\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{v}^2\left(t\right)\mathrm{d}t}$

Be sure to show your working in your writeup. On the same graph, with x range 0 to 500, plot $C\left(\tau \right)$ with $\omega =1/2\pi$ and the VACFs from your liquid and solid simulations. What do the minima in the VACFs for the liquid and solid system represent? Discuss the origin of the differences between the liquid and solid VACFs. The harmonic oscillator VACF is very different to the Lennard Jones solid and liquid. Why is this? Attach a copy of your plot to your writeup.

$x\left(t\right)=A\cos (\omega t+\varphi )$

Differentiating gives:

$v\left(t\right)=-A\omega \sin (\omega t+\varphi )$

$C\left(\tau \right)=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{A}^2{\omega }^2\sin (\omega t+\varphi )\sin (\omega (t+\tau )+\varphi )\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{A}^2{\omega }^2{\sin }^2(\omega t+\varphi )\mathrm{d}t}$

Using the fact that

$\sin \alpha \sin \beta =\cos \alpha \cos \beta -\cos (\alpha +\beta )$ and ${\sin }^2\alpha =\frac{1}{2}(1-{\cos }^{2}2\alpha )$

we can substitute to give:

$C\left(\tau \right)=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}(\cos (\omega t+\varphi )\cos (\omega t+\omega \tau +\varphi )-\cos (2\omega t+\omega \tau +2\varphi ))\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\left(\frac{1}{2}(1-\cos (2\omega t+2\varphi ))\right)\mathrm{d}t}$

we can also use the product-to-sum formula:

$2\cos \theta \cos \varphi =cos(\theta -\varphi )+\cos (\theta +\varphi )$

$C\left(\tau \right)=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}(\frac{1}{2}(\cos (-\omega t)+\cos (2\omega t+\omega \tau +2\varphi ))-\cos (2\omega t+\omega \tau +2\varphi ))\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\left(\frac{1}{2}(1-\cos (2\omega t+2\varphi ))\right)\mathrm{d}t}$

$C\left(\tau \right)=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}(\cos (-\omega t)-\cos (2\omega t+\omega \tau +2\varphi ))\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}(1-\cos (2\omega t+2\varphi ))\mathrm{d}t}$

$C\left(\tau \right)={\left[\frac{t\cos (-\omega \tau )-\frac{1}{2\omega }\sin (2\omega t+\omega \tau +2\varphi )}{t-\frac{1}{2\omega }\sin (2\omega t+\omega \tau +2\varphi )}\right]}_{-\mathrm{\infty }}^{\mathrm{\infty }}$

$C\left(\tau \right)={\left[\frac{\cos (-\omega \tau )-\frac{1}{2\omega t}\sin (2\omega t+\omega \tau +2\varphi )}{1-\frac{1}{2\omega t}\sin (2\omega t+\omega \tau +2\varphi )}\right]}_{-\mathrm{\infty }}^{\mathrm{\infty }}$

$C\left(\tau \right)=\frac{\cos (-\omega \tau )-0}{1-0}$

$C\left(\tau \right)=\cos (-\omega \tau )$

$C\left(\tau \right)=\cos \left(\omega \tau \right)$ Tick, good. In theory papers, ensure if you break up equations with "using the fact that e.t.c you complete the sentence. Example: Using the fact that, <equation> it can be seen.... even if you paragraph the equation, ensure you finish the sentence with a full-stop and don't start the continaution of the sentence after the equation with a capital letter.

The minima in the VACFs represent the change in direction of an atom, in the solid case this is an atom oscillating, with the oscillation eventually becoming zero. The atoms in a solid oscillate because they are fixed in position. For the liquid, the atoms are not fixed in position so they separate from the initial conditions due to Lennard Jones repulsions and come to an equilibrium much faster.But more, the first peak represents the time at which all particles have collided at least once

TASK: Use the trapezium rule to approximate the integral under the velocity autocorrelation function for the solid, liquid, and gas, and use these values to estimate D in each case. You should make a plot of the running integral in each case. Are they as you expect? Repeat this procedure for the VACF data that you were given from the one million atom simulations. What do you think is the largest source of error in your estimates of D from the VACF?

For the smaller simulations, the diffusion constants were:

Gas: 3.2945874

Liquid: 0.0978888780249

Solid: -0.000184298225191

For the million atom case, the diffusion constants were:

Gas: 3.26846579767

Liquid: 0.0900914762785

Solid: 4.55294848307e-05

These are as expected - the diffusion constants should be large for gas and almost zero for solid. The largest source of error is likely to be in the calculation of the integral using the trapezium. Because the trapezium rule divides the curve up into trapezia, they are consistently smaller than the segment of the curve leading to an underestimate. This error will be small because the curve has been broken up into many trapezia (one between each timestep) but the error may still be significant. Tick

Report

Abstract

Various systems were modelled using LAMMPS, a large scale atom simulator, applying the Lennard-Jones pairwise potential. The ideal gas law was tested against the modelled system and found to deviate significantly. Heat capacities for a system at different densities were calculated, showing it to decrease as temperature increases or density decreases. Radial distribution functions were computed for gas, liquid and solid states. Diffusion coefficients were also calculated for gas, liquid and solid states via two methods giving similar results, suggesting they are both good methods. Never say "various systems" whilst writing scientifically. What systems have you modelled and why? Additionally, we have been modelling the dynamics and the diffusive properties of phase in this lab - it's good that we've explored different methods and they compare, but you should tie this to the underlying theme. "The diffusion coffiecients calculated were.. as expected due to the typical physical behaviours of these phases". You should include results in an abstract and comment on your conclusions - not overall depth. Your conclusion is for that depth.

Introduction

You're still writing as a first/second year and could develop this. If you read any research paper out there (as explained in the manual, this report was meant to be more along those lines), they don't have main body/any explanation of technical stuff in the intro. The intro is for setting the scene. Why does the work you've just performed have any relevance? Tie in it with a hot topic - for this lab we could have any phase related/climate change/water and our understanding of its behaviour/something like that. Your derivation (although misplaced) of heat capacity is good, but you're missing the explanation of the first statement and there's a minus sign error on chain rule. But not bad just your style needs a revamp before Bsc/MSci. Modelling a system at the atomic scale is particularly useful because if you can model the smallest scale correctly then both the microscopic and macroscopic properties should be correctly modelled. Large-scale Atomic/Molecular Massively Parallel Simulator, or LAMMPS for short, is a code which models classical molecular dynamics. It models the motions of a set of atoms or molecules and calculates many different physical and thermodynamic properties. The atoms are set up in a strict crystal structure and then "melted". In this experiment, the Lennard-Jones pairwise potentials were used. The Lennard-Jones potential is given by:

$V=4ϵ({\left(\frac{\sigma }{r}\right)}^{12}-{\left(\frac{\sigma }{r}\right)}^6)$

$V$ is the potential and $r$ is the bond length. The well-depth is given by $ϵ$ and is easily confirmed by setting the derivative of the potential to zero to find the equilibrium bond length and then calculating the potential. $\sigma$ gives the bond length at zero potential.

The heat capacity describes how easy it is to heat up a material. A high heat capacity means that a lot of energy is required to increase the temperature of the material.

$C_V=\left(\frac{\partial U}{\partial T}\right)$

It can be shown that:

$\frac{\partial U}{\partial \beta }=⟨E{⟩}^2-⟨E^2⟩$

and

$\frac{\partial U}{\partial T}=\frac{\partial U}{\partial \beta }\frac{\partial \beta }{\partial T}=\frac{\partial U}{\partial \beta }\frac{\partial }{\partial T}\left(\frac{1}{k_{B}T}\right)=\frac{\partial U}{\partial \beta }\frac{-1}{k_B{T}^2}$

Therefore

$C_V=\frac{⟨E{⟩}^2-⟨E^2⟩}{k_B{T}^2}$

The energy calculated by LAMMPS is per atom so

$C_V=N^2\frac{⟨E{⟩}^2-⟨E^2⟩}{k_B{T}^2}$

This allows the heat capacity to be calculated easily from the LAMMPS output.

The radial distribution function gives information about the proximity of other atoms to the atom being studied. It gives the probability that an atom will be found at distance r from the reference atom.

The diffusion coefficient D describes the variation of concentration with distance.

The diffusion coefficient can be linked to the mean square displacement (MSD) like so:

$D=\frac{1}{6}\frac{\partial ⟨r^2\left(t\right)⟩}{\partial t}$

It can also be linked to the velocity autocorrelation function (VACF):

$D=\frac{1}{3}\underset{0}{\overset{\mathrm{\infty }}{\int }}⟨v\left(0\right)\cdot v\left(\tau \right)⟩d\tau$

The velocity autocorrelation function simply correlates the velocity of a particle at one time to the velocity of it at a different time.

Aims and Objectives

You're quite vague writing sweeping statements and I don't think you've quite clocked a purpose for this lab. We were looking at phase, rather than micro to macro where your scale is vague (are you talking about fundamental statistical mechanics or molecular to macro?), and how the dynamic and diffusive properties of phase vary with thermodynamic parameters such as temperature and density. In your BSc/MSci, you're very welcome to use bullet points here - it might heighten some clarity for both you and the reader. The aim of these experiments was to use data computed by large simulations of atoms to gain estimates for a variety of physical and thermodynamic properties.Very broad objective! In particular to use the Lennard-Jones potential to model interactions at the atomic scale to gain understanding of the macroscopic effects of changing certain parameters. If the microscopic modelling is valid, the macroscopic models we already use should tally with the results gained by these simulations. These simulations were run by "melting" a strict crystal structure. Therefore, if the Lennard-Jones parameters are known, many real systems could be modelled effectively by these methods.Vague

Methods

In a computational report, start with the basics - the model. You've gone straight into describing the interactions! Structure - conditions - forcefield - interactions. Then describe the methods used to measure the properties. Lennard-Jones interactions were cut-off after $r^{*}=3\sigma$. This is justified since the total contribution to the Lennard-Jones beyond this point is -0.00329 which is negligible. This was calculated by computing the integral of the potential between $r^{*}=3\sigma$ and $r^{*}=\mathrm{\infty }$.

5 LAMMPS simulations were run for a simple cubic lattice with reduced density of 0.8. An initial crystal structure was ‘melted’ to a liquid. Each simulation was run with a different timestep (0.0001, 0.0025, 0.0075, 0.01, 0.015), in order to determine a suitable timestep for future simulations. Time, total energy, temperature and pressure were recorded for each simulation.

Temperature was varied for 2 sets of simulations under isobaric-isothermal conditions (NpT), each at a different constant pressure. The density was recorded, as well as precise values for temperature and pressure due to the way the system is monitored and controlled.

Temperature was varied again for 2 sets of simulations, this time under the microcanonical ensemble (NVE), at two constant densities. Volume, total energy, temperature and number of atoms were recorded and used to calculated heat capacities per unit volume. An example input script can be found here: File:Jef15D0.2T2.0.in

Atomic trajectories were recorded for simulations of gas, liquid and solid Lennard-Jones systems to produce radial distribution functions. Specific densities and temperatures were used to ensure the systems were in the correct phase, using a phase diagram. Face-centred cubic lattice was used for the solid case as opposed to the simple cubic for liquid and gas.

Certain densities and temperatures were selected to simulate gas, liquid and solid states again Based on what?. The mean squared displacement (MSD) and velocity autocorrelation function (VACF) data (calculated from the velocities) were obtained. Straight lines were fitted to the MSD data to estimate the diffusion coefficients. Integrals of the VACF data were calculated using the trapezium rule and were used to calculate diffusion coefficients.

Results and Discussion

Figure 1: Plot of total energy against time for differing timesteps

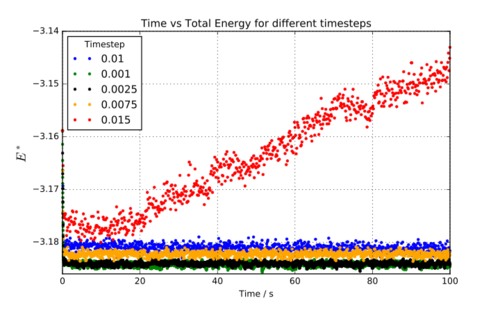
Figure 1 shows the results of the first simulations (varying timesteps). It can immediately be seen that the 0.015 timestep was too big – the energy diverges. The energy of the system should converge so 0.015 can be dismissed immediately. The other timesteps all show converging energies. The lowest energy calculated will be the best estimate. 0.001 and 0.0025 show similar energies. Therefore, 0.0025 is the best timestep to use for these simulations because it offers accuracy but requires fewer computations (for the same total time!) that the 0.001 timestep. The additional accuracy in the energy obtained for 0.001 is outweighed by the computational advantage of using 0.0025.

Figure 2: Plot comparing the computation results to the ideal gas law for two different timesteps

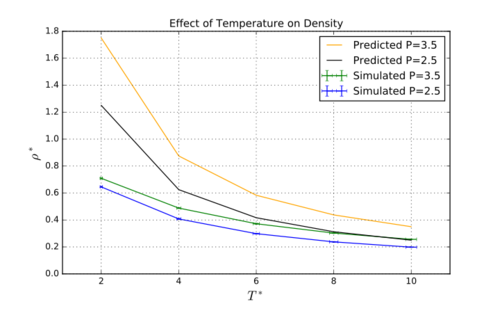
The plots showing the changes in density due to temperature are shown in figure 2. The “predicted” lines were calculated from the ideal gas law, $pV=N{k}_{B}T$. The ideal gas law differs from the modelled data dramatically, and the difference is clearly much larger than the errors involved in the simulation (shown by the errorbars). The simulated density is lower than the density predicted by the ideal gas law. This is due to Lennard-Jones repulsions in the simulated gases causing the particles to spread out. (don't used colloquialisms like 'spread out' in a report - mroe diffuse) In an ideal gas there are no such forces so the particles can coexist closer together. The discrepancy increases as pressure increases because at an increased pressure there are a higher fraction of particles experiencing attractive Lennard-Jones forces which the ideal gas law is not modelling. The discrepancy also decreases as temperature increases because the Lennard-Jones forces become less significant compared to the thermal energy.Tick

Figure 3: Variation of heat capacities with temperature for two densities

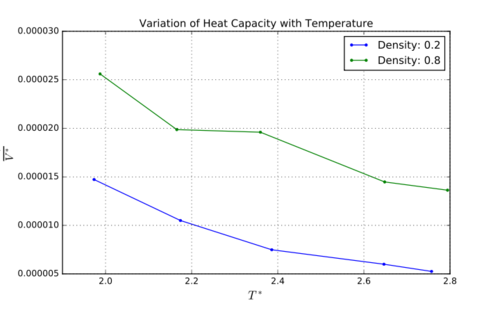
Heat capacity per unit reduced volume was plotted against temperature (figure 3). Heat capacities are lower at lower densities – at higher densities the particles are closer together so heat can be transmitted between particles more effectively. Tick or more energetic states? At higher temperatures, the density of states is greater which means the gap between states is smaller and the transitions become easier. A bump is observed in the heat capacities for density 0.8. This is due to a phase transition which leads increases gram the heat capacity because energy is required to break certain intermolecular bonds.

Figure 4: Radial Distribution Functions for solid, liquid and gas models

Figure 4 shows the RDFs for solid, liquid and gas. The solid shows sharp peaks, which correspond to certain positions in the FCC lattice. The liquid case shows a sharp peak initially which quickly decays and oscillates around 1 and converges. Why? The gas shows a similar pattern but does not oscillate, just quickly converges on 1. This is explained simply by the freedom in gases and liquids. This freedom, which solids do not have, leads to a random arrangement of atoms meaning they are evenly dispersed around the central atom.Would be nice to talk about long-range order here :)

The plots of mean squared displacement against time for each system are shown in appendix. The diffusion coefficients for the smaller simulations (8000 atoms for gas and liquid and 32000 for solid) and for the million atom simulations are given in table 1. The diffusion constants calculated from the VACF data, again for smaller simulations and million atom cases, are given in table 2. There is likely to be a relatively large error in the diffusion coefficients calculated from the MSD data for the gases. This is due to the nature of the plot and fitting a straight line to it. The system takes a while to reach equilibrium so a significant proportion of the data is not on the straight line.Yes, I think this is more due to the nature of gases than the fit to the diffusive region. Manually selecting which data to exclude is far from accurate. To improve the estimate, a computation which simulates a longer time would need to be run, likely with larger timesteps, to give a greater proportion of the data on the straight line. The liquid diffusion coefficients from the MSD data have a relatively small error due to the fact that the straight line was a good fit. The error in the solid data is somewhat irrelevant because the numbers are so obviously small that the key point is that there is no diffusion taking place in the solid state.Tick

The largest source of error for the VACF diffusion coefficients is the numerical integration – trapezium rule. Due to the way the trapezia are ‘drawn’ the trapezia will either undershoot or overshoot, depending on the shape of the curve. This will still be relatively small because the width of the trapezia (timestep) is small. The diffusion coefficients calculated by the two methods should be the same. We can see that although the values are not identical, they are certainly comparable and the discrepancy, between particularly those calculated for the gas states, is likely to be down to the fitting of the data.Tick

Table 1: Diffusion Coefficients calculated from Mean Square Displacement data

	Smaller Simulation	Larger Simulation
State	D / m2s-1	D / m2s-1
Gas	3.034	3.016
Liquid	0.0849	0.0873
Solid	5.83 x10-7	4.39 x10-6

Table 2: Diffusion Coefficients calculated from VACF data

	Smaller Simulation	Larger Simulation
State	D / m2s-1	D / m2s-1
Gas	3.294	3.268
Liquid	0.0979	0.0901
Solid	-1.84 x10-4	4.55 x10-5

Conclusion

The ideal gas law was found to disagree with the results obtained by the simulation to an extent much larger than the error in the simulation. This is due to the simplicity of the ideal gas law which leads to it ignoring important interactions. Heat capacities were calculated at differing temperatures and two different densities showing that the heat capacity decreases as temperature increases and density decreases. The radial distribution functions showed that atoms in the gas and liquid states move freely but solid atoms are not able to move within the crystal structure. Diffusion coefficients were calculated via two methods for each system. Both methods gave similar results, meaning that both are viable methods to use. All of the data collected is easily explained but cannot be easily compared to real systems. The next step must be to model a simple real system computationally and compare the results to real experimental data.Tick but you could have compared to experimental data now?

Appendix

• 
  Small Gas
• 
  Small Liquid
• 
  Small Solid
• 
  Large Gas
• 
  Large Liquid
• 
  Large Solid