Symmetry Workshop 1:background

Background

A symmetry operation is defined as an operation which, when performed on a molecule, leaves the molecule in an indistinguishable state.
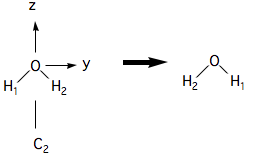
Thus a $C_{2}$ (180˚ rotation) about the $z$ axis in $H_{2} O$ can only be detected if we label specific hydrogen atoms as shown:

The result is indistinguishable, but not identical, as the labels show that the two hydrogen atoms have moved.

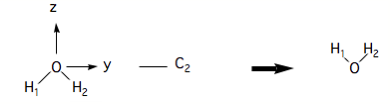
A 180˚ rotation about the $y$ axis is not a symmetry operation, however:

because the result of the operation is not superimposeable on the original.

In finding symmetry operations one needs to develop some skill with 3-dimensional visualisation. In question 2 you will use the graphics display of GaussView to manipulate molecular models and identify symmetry operations.

The complete set of symmetry operations of a molecule form a group.
What this means is that performing any two operations in succession is equivalent to performing a third operation, which is also a symmetry operation.

$σ_{v}^{2} = C_{3} \circ σ_{v}^{3}$

(Notice the convention whereby the molecule moves but the symmetry elements are fixed in space).
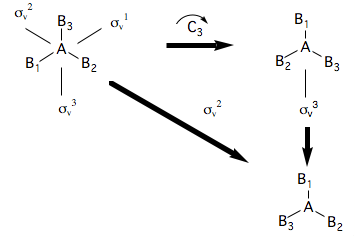
Because symmetry operations can be combined as shown above, in order to identify the group of all symmetry operations of a molecule, one need only identify a few operations called generators. Thus the group of a trigonal planar $A B_{3}$ molecule is $D_{3 h}$ and is made up of the following symmetry operations:

$D_{3 h} = {E 2 C_{3} 3 C_{2} σ_{h} 3 S_{3} 3 σ_{v}}$

where the symbol $3 C_{2}$ is used to denote the fact that there are 3 equivalent $C_{2}$ rotation axes (about each AB bond).
A set of generators is

$D_{3 h} g e n e r a t o r s {C_{3} \to S_{3} \to C_{2} \to σ_{h}}$

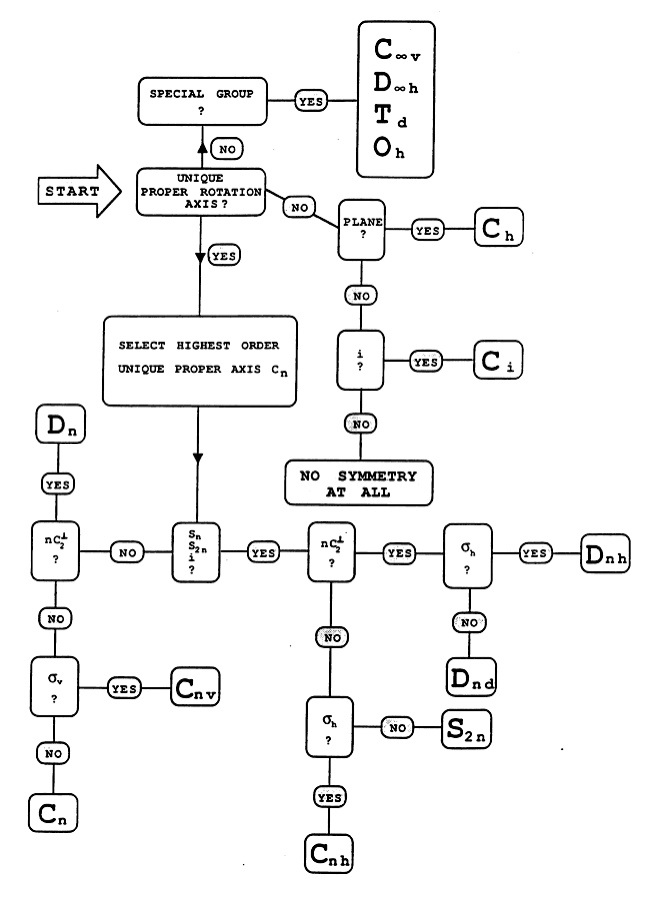
Flowchart

All the symmetry operations of $D_{3 h}$ are combinations of the above sub-set of generators. The process of finding generators can be made systematic using a decision table or flowchart, such as the one given below.

NB
The flowchart also indicates that there are relationships between point groups; they do not exist in isolation. This idea is explored further in questions 3, 4 and 6.