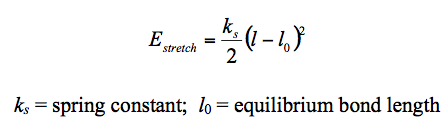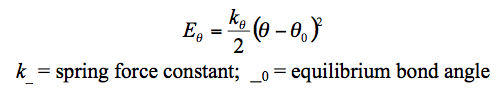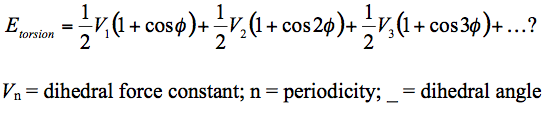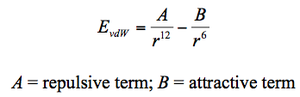Sunkiss pl1208 01

Aim of Experimentation

Specific computational methods (Molecular modelling and semi-empirical DFT) will be implemented to describe and justify the outcome of organic chemical reactions. These modelling experiments will be carried out via the use of different programmes such as MM2 force field parameters (classical method), PM6 parameters (semi-quantum method) and DFT modelling method (Quantum Mechanics) on simple organic molecules. The advantages and limitations of each method is determined via detailed analysis of the results attained. The list defines the different modelling experiments to be carried out

• Hydrogenation of cyclopentadienes to form the dimer

• Nucleophilic addition to a pyridinium ring (NAD⁺ Ananlogue)

• Reactivity of Taxol intermediates

• Regioselective addition of Dichloro-carbene.

• To conclude the usage of the computational software, a mini-research exercise is carried out

Introduction

The importance of computational chemistry is largely seen in modern times where it's importance is not only seen in theoretical advancements but also in allowing highly accurate predictions to be made for chemical reactions to be carried out in laboratories. Computational methods implement specific softwares such as ChemBio3D which allows the total energy of chemical reactions to be calculated.This allows the stability of the products formed to be quantified; allows accurate prediction of individual bond energies. Computational chemistry serves as the 'backbone' for chemical reactions carried out in the laboratories. Furthermore, it also helps towards predictions made for the ideal scale, reaction conditions and expected yield to be attained from the wet reaction to be carried out.

The first modelling technique considered is molecular modelling(MM).(MM) based calculations via the use of MM2 force field parameters treat the molecules classically where newtonian mechanics is implemented to model the molecular system. The method draws parallel to 'viewing' the atoms and bonds as spheres held together by springs. The calculations carried out allow the molecule to be 'modelled' to it's lowest energy conformation. This allows the calculated results to be compared with the experimentally attained results. The overall minimum energy of the molecule is attained via a summation of the individual bond energies (Table 1).

The PM6 parameters is defined as the semi-classical method of modelling. Being a semi-classical method it still functions on the underlying principal of 'viewing' the atoms and bonds as spheres held together by springs. However, there is a specific degree of quantum influence in determining the overall energy where electronic distribution within the molecule is taken into account when calculating the specific bond energies. This enables deviations due to the influence of an electron donating or withdrawing substituent to be observed and have the calculated value to be much more similar to the experimentally attained value as compared to calculations made via the MM2 model.

The last modelling method considered is the Density Functional Theory (DFT), which is a quantum mechanics-based calculation. The method implements the functionals of electron density to accurately describe the excited states allowing the electron's spatial influence to be accounted. This makes the modelling method to give the most accurate optimisation of the structure relative to the other two modelling methods considered.

However, the (MM) method is the most favoured as it is the least expensive method and is well adapted for the provision of excellent structural parameters such as bond distances and bond angles. Also, in the presence of a good force field, the calculated structural results resemble the experimentally determined structures more closely as compared to other computational techniques making this method of analysis accurate to a reliable extent. However, the available parameters depicted only satisfies about 20% of known molecules which limits its applicability. Furthermore, as the electrons and specific orbitals are not implemented in this method, it will not be able to evaluate chemical reactions nor predict the reactivity of specific molecules. Thus, a deviation from actual experimental results is expected.

Table 1: Summarising the Individual bond energies calculated via molecular modelling

No.	Type of bond stretch	Method of calculation	Bond Representation	Equation for analysis
1	Diatomic Bond stretches	Harmonic Oscillator Approximation
2	Triatomic Bond Angles (Bond Angle bending)	Harmonic Oscillator Approximation
3	Tetra-Atomic bond torsions (Dihedral angle rotation)	cell
4	Van Der Waals intections	cell
5	Electrostatic Interactions	cell
6	Hydrogen bonding	cell

The individual atoms are treated as spheres but the overall mass is dependent on each atom's elemental property. The chemical bonds within the molecule are treated as springs which allows the implementation of Hookes Law. The bond strength (stiffness of the spring) is dependant on the type of atoms bonded and type of bond formed (single, double or triple). The individual energies when summated give the total potential energy of the molecule(Table 1). However as seen from table 1, modelling equations are based on bonds found in simple diatomics. This limits the modelling method to simple molecules (usually hydrocarbons) where 'complex' interactions such as Metal-halide interactions are not accounted.

There are different force fields that can be considered for the (MM) calculations such as MM2, MM3 and OPLS-AA. MM2 and MM3 force fields are designed for the use with organic type molecules. The MM3 force field method was generated to deal with problems surfaced in the MM2 method. Both parameter sets were developed by the Allinger group at the university of Georgia for the modelling of small organic molecules.

The Formation and Hydrogenation of the Cyclopentadiene Dimer

Cyclopentadiene has two unsaturated C=C bonds allowing it to readily undergo a [4+2] diels-alder reaction to form the cyclopentadiene dimer. From literature experimental results, it was determined that only the endo-dimer is formed exclusivly.

However, in cycloaddition reactions carried out there is the possibility for both the endo and exo products to be formed. Thus, the reasons for the formation of only the endo product will be analysed and rationalised. Secondly, the hydrogenation of the dimer formed will also be analysed since the dimer has two different alkene bonds present. Thus, there is a possibility for regioselectivity of one C=C bond over the other will be rationalised.

Dimerisation of Cyclopentadiene via [4+2] Diels-Alder cycloadditions

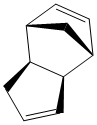
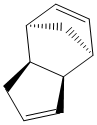
Cyclopentadiene readily undergoes [4+2] cyclo-addition (diels-alder) reaction to form two stereoisomers (exo dimer or the endo dimer).Diagram 1 shows the mechanism of the expected [4+2] cycloaddition and the two dimers that could result.

Dig. 1 Reaction pathway for [4+2] Dimerisation of Cyclopentadiene

Table 2: Comparing Endo and Exo Cyclopentadiene Dimers

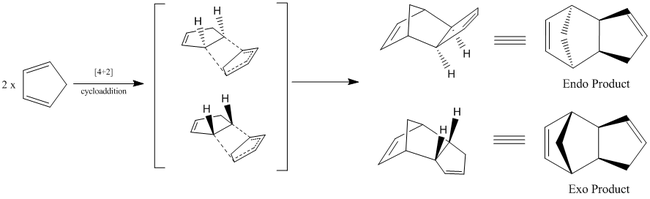
Endo-Dimer	Exo-Dimer

Using Cambridgesoft software 'ChemBio3D', the two possible dimers were optimised using the MM2 force field parameters. This geometrical optimisation (lowest energy configuration) resulted in the exo-dimer to have a lower energy of 31.8777 kcal/mol as compared to the endo-dimer which has an energy of 34.0020 kcal/mol. The product with the lower energy is defined as the thermodynamic product(exo-dimer). Thus, when the dimerisation is left standing under equilibrium conditions which has thermodynamic control, it ideally should have the reaction pathway ending at the more stable product (exo-product) instead of the endo which is energetically less favoured.

However, according to experimental literature, the endo product was formed exclusively instead of the energetically lowere exo-dimer. Although cycloaddition reactions are expected to be reversible, the favourable formation of the dimer makes the backwards reaction almost negligble. This makes the reaction seem irreversible. Being an irreversible reaction, the cycloaddition takes place under kinetic control instead of thermodynamic control. Under kinetic control, the reaction pathway that is most readily attained is favoured making the relative stability of the final products irrelevant. Instead, it is the stability of the transition state that functions as the 'pre-determining factor'. The energetically more stabilised transition state gives a smaller activation energy barrier which is more readily overcomed. The faster the attainment of the transition state the more readily the product is achieved.

This explains why the higher energied endo product is formed instead of the exo product. The cyclo-addition occurring under kinetic control yields the endo-product since it has a transition state of lower energy.. This is represented in the energy diagram below (endo=blue exo=black).

Dig. 3 Reaction pathway for Endo Vs. Exo

Table 3: Comparing the specific bond energies of both the Endo and Exo Dimers

Type of Dimer	Exo	Endo
Images
Bend (Kcal/mol)	20.5681	20.8399
Angle(Kcal/mol)	-178.6	-45.2304
Torsion(Kcal/mol)	7.6559	9.5143

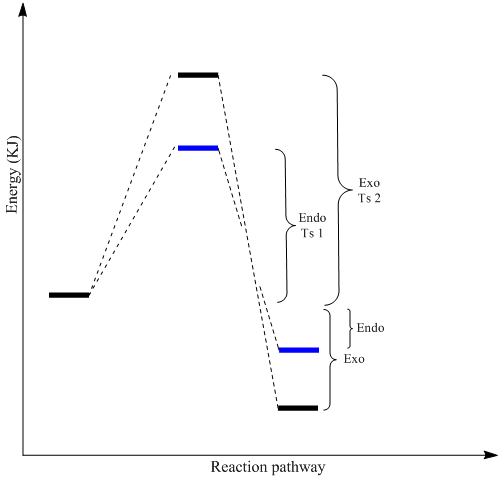
All values provided in table 3 are in Kcal/mol; the degree of accuracy provided is equal to that from the MM2 output. Although the accuracy of the MM2 calculations is expected to deviate from experimental values, the inaccuracies have been accounted for in the total energy of each dimer by keeping the value to a single decimal place. The dihedral angle across the new C-C bond formed via cycloaddition was analysed and the results for the various energies are represented in the table 3. The components representing the strain show that the endo-dimer has a smaller dihedral angle of -45.23 Kcal/mol as compared to the exo-dimer which has a value four times larger (-178.6 Kcal/mol). This is indicative that the double bonds are much closer in space for the endo dimer as compared to the exo-dimer. This results in the pi-electron systems to be spatially closer to each other resulting in more significant repulsions. The endo-dimer having greater repulsions should be destabilised to a greater extent and be less favourably formed as compared to the exo-dimer. This is indicative that the MM2 calculations are made for the expected product under thermodynamic control and not kinetic control. Thus, it can be concluded that the MM2 force field method predicts the major product if it was under thermodynamic control instead of the actual kinetic control reaction pathway observed for the cyclopentadiene dimerisation.

The endo-dimer is the kinetic product under kinetic control as it has a more stable, lower energy transition state. Thus, stereo-electronically, the endo-dimer transition state has a greater amount of HOMO-LUMO interactions as compared to the exo-dimer. This enables a greater extent of stabilisation for the endo forming transition state. The selectivity for the higher energied-endo dimer can also be explained by the Woodward-Hoffman rules or the frontier orbital theory (diagram below).

Dig. 4 Frontier Orbitals for Exo and Endo Dimers

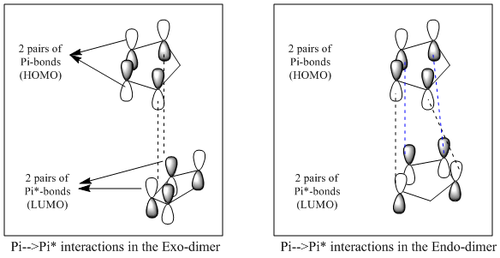
In the endo-dimer, there is a greater extent of orbital overlap between the diene and dienophile (Pi-->Pi* electron donation). This brings about a greater extent of stabilisation since the diene approaches the dienophile from the 'top' allowing greater in-phase orbital interaction. The black dotted lines represent the two C-C sigma bonds formed due to cycloaddition while the blue dotted lines represent the secondary stabilising orbital overlaps that further stabilise the transition state. However, for exo-dimer formation, the diene approaches the dienophile from a 'side along side' basis. This results in the overlapping of only the extreme end C=C orbitals. Thus, it results in the formation of the 2 C-C sigma bond without the presence of any additional orbital interactions.

The endo dimer having greater HOMO-LUMO interactions, makes it a more stable transition state and thus the kinetically driven product of the cycloaddition. The importance of the secondary orbital interactions is seen when cyclopentadiene is replaced with cyclopentene which only has 1 C=C bond. This means there will not be any pi bonds for secondary orbital interactions. This resulted in a reaction to give only 29% of the endo product even with longer reaction time . This is because there are no additional interactions to make the endo-transition state more stable than the exo transition state. In conclusion, because of the secondary stabilising effect, the endo dimer has a lower energy transition state making it more readily achieved and thus the exclusive product of the cycloaddition reaction under kinetic control.

The limitation of the MM2 method is seen since the relative energies of the specific transition state's are not considered where only the final energies are considered in determining which isomer dominates. This makes the (MM) method of computational analysis more accurate only under thermodynamic conditions and not kinetic conditions. Thus limiting the types of reactions that can be considered for this ,mode of calculation.

Hydrogenation of the Endo-Dimer

From Section 3.2 it has been conclusively rationalised that the dimerisation of cyclopentadiene occurs under kinetic control to give the endo-product exclusively. Thus, hydrogenation with one equivalence of H₂ gas will be considered only for the endo product. As the endo product has two unsaturated C=C bonds, hydrogenation is initially expected to be able to occur at either bonds as represented in the reaction scheme (Diagram 5). Based on experimental evidence, hydrogenation is regioselective and dependant if the reaction is thermodynamically or kinetically driven.

Dig. 5 Reaction scheme for both possible hydrogenation

The two hydrogenated products molecular 1 (left) and molecule 2 (right) are represented below. The formation of molecule 1 involves the hydrogenation of the cyclohexene double bond whereas the formation of molecule 2 involves the hydrogenation of cyclopentene double bond. Analysis of the molecular structures show that the mechanism and orbitals involved in the hydrogenation at both regions are very similar (Table 4). They are in very similar environments making the preference for regioselectivity to not be steric-dependent but instead be energetically dependent.

Table 4: Comparing the molecular structures of both Hydrogenated Products

Molecule 1	Molecule 2

To determine the lowest energy, the hydrogenated products were subjected to (MM) via application of the MM2 forcefield parameters. This gave rise to the minimised total energy as a summation of the individual bond energies. Table 5 summarises the results attained for both molecules.

Table 5: Comparing the Specific Energies for both Hydrogenated Products

Properties	Hydrogenated product 1	Hydrogenated product 2
Diagram
Stretch (Kcal/mol)	1.1006	1.2659
Bend (Kcal/mol)	14.5433	19.8063
Torsion (Kcal/mol)	12.5088	10.8698
Non-1,4 Van Der Waal(Kcal/mol)	-1.0765	-1.2207
Van Der Waals (VDW) (Kcal/mol)	4.4978	5.6394
Dipole-Dipole (Kcal/mol)	0.1408	0.1621
Angle (C=C) (deg)	116.4	107.2
Total Energy (kcal/mol)	31.1701	35.6953

Comparing the overall energy of both molecules, molecule 1 is lower in energy (31.17 Kcal/mol) than molecule 2(35.70 Kcal/mol) by 4.53 Kcal/mol. Thus, the hydrogenation of the cyclohexene alkene bond gives rise to the more stable product as compared to hydrogenation of the cyclopentene alkene bond. This makes molecule 1 to be more thermodynamically favoured over molecule 2. The total energy of the endo-dimer was 34.002 Kcal/mol but the hydrogenated product is of a lower energy. When this is compared with the energy levels of both hydrogenated products it is noticed that the formation of molecule 1 is an exothermic reaction. This results in the lower energied, thermodynamically more favoured product to be formed. The formation of molecule 2 is an endothermic reaction where hydrogenation results in an increase of the total energy making it thermodynamically less favoured.

Analysis of the individual contributing bond energies in table 5 shows that the overall difference in energy is mainly due to the difference in the angle (bending) energy and Van der Waals forces of interaction. Comparing the angles across the C=C double bonds shows that molecule 1 has an angle of 116 deg while molecule 2 has a bond angle of 107 deg. The ideal angle for the SP² carbon bonds is 120 deg. The greater the deviation from the ideal angle the greater the angle strain. This explains why molecule 2 having a more strained bond angle has a higher bending energy of 19.8063 Kcal/mol. This strain can also be justified theoretically by considering the nature of the double bond which induces restricted rotation due to the pi bond. This makes the ring overall more rigid, the presence of the C=C bond in different regions influences the overall molecule's rigidity to different extents. For the endo-dimer, the 6-membered ring and the bridge in that ring influence the overall energy to a greater extent than the 5 membered ring. The presence of the C=C bond in the 6 membered ring induces greater rigidity as compared to the C=C bond being present in the 5 membered ring. This explains why molecule 2 having the C=C bond in the 6-membered ring has a higher bending energy than molecule 1 making it less stable.

In conclusion, due to the greater strain imposed and being of a higher energy than the starting material, molecule 2 is not the thermodynamically favoured product. Molecule 1 on the other hand is the product formed under thermodynamic control. As insufficient data is attained about the nature of the transition state for the reaction, the relative energies of the transition state cant be determined. Thus, it can't be concluded which would be the kinetically driven product via hydrogenation of the endo-dimer. When compared with the experimentally carried out hydrogenation, it is usually carried out with a metal catalyst (Ni or Pd complexes) that facilitates the release of ring strain. Thus, the computer modelling exercise shows that the bond strain is the key determinant for determining the thermodynamic product. This also explains why a metal catalyst is used in wet experiments.

Futher Considerations

Table 6: Tetrohydrogenated Product

It has been found in literature that the doubly reduced dialkenes are not hydrogenated as readily but it would happen over a longer reaction duration.. The overall energy of the tetrahydrogenated molecule is 32.3702 Kcal/mol. This was about 1.2 Kcal/mol higher than the starting material. Upon the first hydrogenation of molecule 1. The torsion energy of this molecule is 15.8120Kcal/mol which is significantly higher as compared to the endo-dimer's torsion. This explaining why the reaction took a much longer time to form the tetrahydrogenated product. The second hydrogenation was endothermically driven to form the higher torsion product which does not readily occur as the tetrahydrogenate product is less stable.

Stereochemistry of Nucelophilic addition to pyridinium ring (NAD⁺ analogue)

This section investigates the face from which a nucleophile approaches and attacks the electron deficient centre in the pyridinium ring. Two examples will be considered where each will be using a different pyridinium compound. Conclusions about the direction from which a nucleophile attacks are drawn via the analysis and rationalisation of the two examples.

Example 1 : Investigating the optically active derivative prolinol (5) via a nucleophilic attack from a Grignard reagent

Dig. 7 Reaction of N-Methyl Pyridoxazepinone with Methyl Magnesium Iodide

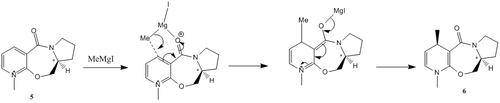
The optically active prolinol derivative (5) reacts with the grignard reagent methyl magnesium iodide to alkylate the pyridine ring at the para position. According to literature, this reaction results in the absolute stereochemistry(6). The regioselectivitiy and stereoselectivity of the nucleophilic attack is rationalised to be due to chelation. The incoming grignard reagent has the electropositive Magnesium mental centre readily coordinating to the electronegative oxygen of the carbonyl. It is the chelative effect that influences the face via which the methyl group attacks the pyridine ring. This addition of the methyl group occurs via a nucleophilic addition reaction (Diagram 7). Thus, the relative stereochemistry of the carbonyl group has to be taken into account towards determining the direction from which the nucleophile attacks.

Dig. 8 Both possible nucleophilic attacks brought about by the chelation

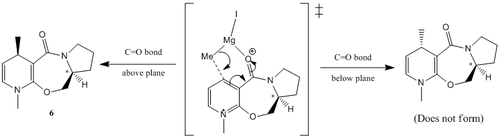
This brings about two possible stereoisomers prior to the nucleophilic attack. (i) The carbonyl group is above the 7-membered ring or (ii) The carbonyl group is below the 7-membered ring (Diagram 8). The two stereoisomers are of the same molecule but of different bond orientations, this makes them conformers of each other. Both conformers were analysed, where their minimum energy was computed via the use of the MM2 force field parameters. However, the MeMgI Grignard reagent was not added into the energy minimisation since ChemBio3D was unable to recognise the Mg as an metal atom. This resulted in an software error when the Grignard reagent was included for the calculations. This is due to the limitations of the MM2 model since it is based on bonds found in simple diatomic molecules.Thus the MM2 calculations is not able to model the metal-type bonding interactions. Thus, as mentioned in the introduction, the MM2 model is limited to simple molecules and would break down if it is attempted with co-ordination type or non-classical interactions.

Thus, energy of the starting material (5) was minimised to determine both possible conformers. The MM2 method of minimising energy is based on the logic that it could get 'stuck' in different potential energy wells if the starting points are different. This results in giving the pseudo-minimisation which is not the lowest energy level of the reactant making it inaccurate. Thus, a different number of starting points were investigated by varying the dihedral angle between the carbonyl group and the aromatic ring (Graph 1). From the graph, the total minimum energy of the conformer is attained when the carbonyl group is 12° above the plane of the aromatic ring.

Graph 1 : Varying the dihedral angle against total energy of the molecule

Table 6  : Comparing the specific energies for the 3 distinct conformers

	Conformer 1	Conformer 2	Conformer 3
Carbonyl relative position	Above plane	Above Plane	Below Plane
Image
Stretch(Kcal/mol)	2.0276	17.1799	8.4974
Bend(Kcal/mol)	14.1479	178.1686	83.8502
Stretch-Bend (Kcal/mol)	0.1333	-4.6402	-2.6517
Torsion (Kcal/mol)	5.2352	62.5344	88.9772
Non-1,4 VDW (Kcal/mol)	-0.6069	2.0556	7.4923
1,4 VDW(Kcal/mol)	16.5396	41.6637	35.0133
Charge/Dipole(Kcal/mol)	9.6711	9.2275	-15.2838
Dipole/Dipole (Kcal/mol)	-3.9810	-4.1944	-3.0647
Total Energy	43.1641 kcal/mol	301.9952 kcal/mol	202.8303 kcal/mol
Dihedral angle	12 deg	125 deg	-105 deg

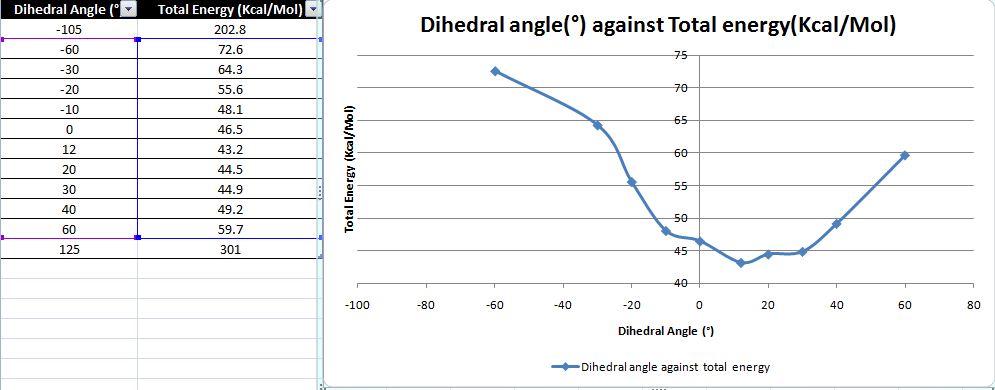
From table 6, the dihedral angle of a positive value is indicative of the carbonyl bond being above the plane relative to the aromatic ring. In contrast, when the polarity of the dihedral angle is negative it is indicative of carbonyl bond being below the plane relative to the aromatic ring. From the graph 1 and table 7, it is concluded that there are no low energy conformations when the carbonyl bond is below the plane. Thus, making the product to be of an absolute stereochemistry where the methyl group via the grignard reagent always coordinates to the carbonyl group orientated above the plane of the ring. This brings about the chelating effect and has the nucleophilic addition to give product (6).

Table 7 : Comparing the specific energy for the 2 possible products

	Conformer 1	Conformer 2
Methyl relative position	Above plane	Below Plane
Image
Stretch(Kcal/mol)	2.2149	2.2524
Bend(Kcal/mol)	16.2579	16.3708
Stretch-Bend(Kcal/mol)	0.3273	0.3265
Torsion(Kcal/mol)	5.8234	5.5423
Non-1,4 VDW(Kcal/mol)	-0.2602	-0.3180
1,4 VDW(Kcal/mol)	17.5108	17.5625
Dipole/Dipole (Kcal/mol)	-4.3629	-4.3336
Total Energy	37.5112 kcal/mol	37.4029 kcal/mol
Dihedral angle	-74 deg	70 deg

Table 7 depicts the two possible conformers, although only conformer 1 is formed via the nucleophilic attack. The purpose of calculating the specific energy of the two products is to rule out thermodynamic control as a reason for absolute stereoselectivity. This is because both the possible products above or below the ring when minimised give rise to products of very similar total energies with a difference of only 0.1 Kcal/mol making it an insignificant difference. Thus, the energy difference is too small to reason the absolute stereoselectivity due to thermodynamic control. Instead it narrows the reason to be due to the chelate effect that results in the the methyl group to be 'depositied' on the same face as that of the carbonyl bond relative to the ring.

Example 2 : Investigating the reaction of N-methyl Quinolium Salt with Aniline

This example is built on the previous example where example 2 involves aniline acting as the nucleophile instead of a Grignard to react with the pyridinum ring in the N-methyl Quinolinum Salt. The reaction involves the insertion of the -NHPh group onto the para position of the ring via nucleophilic addition (Diagram 8). According to literature, the incoming nucleophile attacks from the 'face' of the plane opposite to that of the C=O carbonyl group. Another literature source defines the reaction with aniline as the nucleophile to be antropenantioselective; resulting in the complexes formed to be termed as chiral amide transfer agents. This seteroselectivity is expected to be due to a steric control and will be investigated and rationalised via the application of molecular modelling methods.

Dig.8 Reaction pathway for Nucleophilic attack by Aniline

Table 8 : Comparing the specific energies of both conformations of the reactant

	Conformation 1	conformation 2
Carbonyl relative position	Above plane	Below Plane
Image
Stretch (Kcal/mol)	3.8973	3.9411
Bend(Kcal/mol)	11.5815	11.5979
Stretch-Bend(Kcal/mol)	0.4032	0.4007
Torsion (Kcal/mol)	9.9928	9.6530
Non-1,4 VDW(Kcal/mol)	4.0695	3.5460
1,4 VDW(Kcal/mol)	29.3333	29.4347
Charge/Dipole(Kcal/mol)	9.0388	9.0174
Dipole/Dipole (Kcal/mol)	-4.8827	-4.8857
Total Energy	63.4337 kcal/mol	62.7051 kcal/mol
Dihedral angle	21 deg	-20 deg

Table 8 shows the total energy minimisations of both possible conformations. The difference in both formations is that (i) The carbonyl bond above the plane relative to the aromatic ring (ii) The carbonyl bond below the plane relative to the aromatic ring. The total energy of both forms varied only by 0.7 Kcal/mol making them very close in energy. Unlike example 1 where the two forms were conformers of each other, here there is negligible difference in energy between the two forms. This was indicative that in example two, both conformations are equally probable. Thus, both have to be accounted for in the reaction with the approaching nucleophile. Also, as the energies of both conformations are very similar there is no thermodynamic influence for one conformation over the other. This also suggests that the dominance for one conformer over the other lies in the energy of the products formed instead of the reactants.

Table 9 : Comparing the specific energy of the 2 conformations of the product

	Conformation 1	conformation 2
Nucleophile attacking position	Above plane	Below Plane
Image
Stretch(Kcal/mol)	4.2200	6.4949
Bend(Kcal/mol)	18.1947	25.4098
Stretch-Bend (Kcal/mol)	0.8199	1.0082
Torsion(Kcal/mol)	4.3644	11.5600
Non-1,4 VDW(Kcal/mol)	2.0397	5.8101
1,4 VDW(Kcal/mol)	34.1950	35.6711
Dipole/Dipole(Kcal/mol)	-6.5875	-6.0762
Total Energy	57.2462 kcal/mol	79.8779 kcal/mol
Dihedral angle	66 deg	-72 deg

The nucleophile having the bulky phenyl group adjecent to the nitrogen heteroatom makes it highly 'steric-consious'. This will result in the bulky nucleophile to approach the pyridinum ring via the least hindered pathway. Based on the diagrams in table 9, it is seen that the nucleophile completely avoids the carbonyl group. It makes it favourable for the nucleophile to attack from opposite projection of the carbonyl bond. This is mainly due to the electron-electron repulsion expected from the lone pairs on both heteroatoms nitrogen and oxygen in the nucleophile and carbonyl respectively. When compared with the total energy of both product forms (table 9), it is noticed that the total energy via the nucleophile attacking from the top face is 13 Kcal/mole lesser than conformer via an attack from the bottom face. This makes the conformation via the top face to be energetically more stable and favoured. This rationalises the literature intitially discussed where the formation of 1 stereoisomer dominated over the other. Being the lower energy product it would be thermodynamically more favoured as well.

The positive dihedral angle is indicative that the nucleophile is added from the top face with respect to the aromatic ring and this in turn resulted in the dihedral angle of the carbonyl relative to the plane of the ring to be negative indicating that it is in the opposite plane relative to the nucleophile.

Comparing the magnitude of the total energy with respect to the reactant (62.7 Kcal/mol) showed that the product had a significantly lower energy level. This can be rationalised as being due to the ability of the nitrogen group to bring about further stabilisations via dipole dipole interactions with the electrophilic pyridinum ring. Also. the product formation was thermodynamically more favoured as it also allowed the (+) on the electronegative nitrogen to be removed.

It is concluded that the attack of the nucleophile is under steric control and readily occurs under thermodynamic control. It is not determined if it is the same coformer formed under the kinetic control. Thus, additional analysis and experiments should be carried out on the transition state to determine its energy level. It is key in determining if the product formed is also kinetically inclined.

Lastly, as the experiment is to be carried out in wet conditions, the influence of solvent should also be taken into consideration for a more accurate understanding on which product is more stable. This is important for this compound since the presence of electronegative groups would allow interactions with protic solvents (H-bonding) that could greatly stabilise one product isomer over the other. Thus, the influence of solvents should also be looked into for future considerations.

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

The total synthesis of Taxol (an important drug in the treatment of ovarian cancers) involves the formation of a key intermediate which is readily isolated due to its overall ring stability. According to literature, the intermediate exhibits atropisomerism which results in formation of 2 different stereoisomers with respect to the orientation of the carbonyl bond (Diagram 9). Being atropisomers, they are not readily interconverted in situ; the correct experimental conditions have to be imposed to ensure the correct intermediate is formed so as to allow the successive stereochemistry-orientated reactions to occur and produce the target molecule of the correct stereochemistry. Thus, computational modelling efforts will be adopted to determine the specific conditions that allows one isomer to be the predominant product. This will allow the ideal wet conditions to be established towards effective target synthesis of the taxol molecule. Also, the effect known as 'Hyperstable Alkenes' will be investigated with reference made to the intermediate of Taxol.

Key Intermediates towards the Synthesis of Taxol

Dig.9 Atropisomers of the Key intermediate towards Taxol synthesis

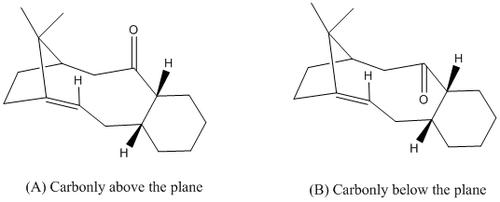
According to literature,(A) and (B) isomers of the key intermediate would have isomer(A) interconverting to (B) when left standing under equilibrating conditions. This implies that (B) is thermodynamically more stable than (A) making it the favoured conformation under thermodynamic control. This is verified by means of molecular modelling where the MM2 forcefield parameters are implemented to determine the minimum energy of the 2 isomers (Table 10). Similar to earlier sections the minimisations were carried out from different 'starting' points to avoid the trapping in a potential energy wells.

Table 10 : Comparing the specific energies of the 2 atropisomers of the Intermediate

	Isomer A	Isomer B-1	Isomer B-2
Carbonyl relative position to adject H atom	Same Side	opposite side	opposite side
Image
Stretch(Kcal/mol)	3.1417	2.5752	2.4811
Bend(Kcal/mol)	20.4401	10.7213	10.8893
Stretch-Bend(Kcal/mol)	0.5049	0.3195	0.2942
Torsion(Kcal/mol)	21.9620	19.6097	17.3102
Non-1,4 VDW (Kcal/mol)	-0.6339	-1.31460	-1.7058
1,4 VDW(Kcal/mol)	14.3452	12.5536	12.4299
Dipole/Dipole (Kcal/mol)	0.0091	-0.1838	0.1427
Total Energy	59.7690 kcal/mol	44.2809 kcal/mol	41.8416 kcal/mol

Table 10 shows the lowest energy configuration for both isomers. To facilitate better understanding, the 6 membered ring is coloured black and the hydrogen adjecent to the carbonyl is in yellow. Comparing the total energy of (A) against (B) shows that (B) which has the carbonyl in the opposite plane to that of the hydrogen (yellow) is significantly more stable than (A) quantitatively by 18 Kcal/mol. Thus, (B) has an carbonyl orientation that is thermodynamically more stable as compared to that of (A) making (B) the dominating isomer under thermodynamic control. This is in agreement with earlier mentioned literature which states that (A) isomerises to (B) when left standing.

Analysis of Isomer B showed that there were two possible chair conformations adopted by the cyclohexane ring. Thus, the chair conformations were swapped to give both forms (Table 10) which showed that one conformatino more was slightly more stable (3 Kcal/mol) than the other. This could be attributed to the sterics involved where one form of the chair orientation resulted in a lesser steric influence as compared to the other.

(B) was overall a much lower energy than (A) which was rationalised to be due to the steric influence imposed. The carbonyl group having an orientation to be on the same plane as that of the adjecent hydrogen (yellow) will result in a greater degree of steric clash with the hydrogen atoms on the same side of the plane and the bridge head methyl group. Thus, this steric clash is avoided when the carbonyl group is in the opposite plane of the bridge head such as that in (B). Drawing parallels with the bend energy, (A) has a significantly much higher bend of 20 Kcal/mol as compared to (B) of 10 Kcal/mol. This could be due to the relative position of the carbonyl bond. In (A), the bond is above the plane and experiences the strain of the cyclic system and the steric clashes earlier discussed. This results in the sp² angle to be 109.4 deg but in (B) it would have the cyclic strain but not the steric clashes which results in an angle of 118.2 deg. Thus, (B) has a angle closer to the ideal angle of 120 deg. This results in lesser strain which is depicted by a smaller bend energy giving an overall lower total energy.

The difference in the total energy was 17.9274 Kcal/mol when carried out under the MM2 force field parameters and when it was carried out under the MMFF94 parameters the individual values were significantly different but the difference in total energy was 18.9458 Kcal/mol which is very close to the MM2 calculated difference. Thus both showed (B) to be the thermodynamically more stable isomer.

In conclusion, (B) is the thermodynamically more favourable product and when the reaction is done under reversible equilibrating conditions, the formation of (B) over (A) as the key intermediate can be expected. However, insufficient analysis is done on the transition state energy levels to determine which predominates under kinetic control as well.

Extraordinary Reactivity of Alkenes

The C=C alkene bond having a bond order of two is expected to be an electron dense reaction site. Being electron dense, it is nucleophilic making it ideally susceptible to an electrophilic attack or an addition reaction across the double bond as the pi-bonds are more reactive than the sigma bonds due to weaker orbital overlaps. However, in the environment such as that of the Taxol intermediate, C=C bond is experimentally observed to have slower reaction rates. Reacting slower would mean the C=C is considerably less reactive which makes it an 'Hyperstable Alkene'. A hyperstable alkene is one that experiences a lesser strain as compared to the parent hydrocarbon due to the adjecent bridgehead. Qualitatively, this is observed by calculating the Olefin Strain Energy (OSE). The OSE is calculated via comparing the torsion energy of the alkene with the torsion energy of the hydrogenated equivalent (Parent). When the torsion is lesser than that of the parent, it is hyperstable (Table 11).

Table 11 : Comparing the torsion energy of the hyperstable alkene against the parent hydrocarbon

	Intermediate (Alkene)	Parent Hydrocarbon
Image
Stretch (Kcal/mol)	2.4700	4.9197
Bend(Kcal/mol)	10.8592	23.9431
Stretch-Bend(Kcal/mol)	0.2925	1.2070
Torsion (Kcal/mol)	17.3565	23.4667
Non-1,4 VDW(Kcal/mol)	-1.6846	2.1497
1,4 VDW(Kcal/mol)	12.4177	18.9016
Dipole/Dipole (Kcal/mol)	0.1418	0.0000
Total Energy	41.8532 kcal/mol	74.5877 kcal/mol

The hyperstable alkene present in the intermediate has a lower torsion energy of 17.4 Kcal/mol than the parent hydrogenated molecule of 23.5 Kcal/mol. The olefin strain energy (OSE) is calculated as (17.3565-23.4667)= -6.1102 Kcal/mol which is lesser than zero. The intermediate is indeed of a lesser strain than the parent hydrocarbon showing that the C=C bond is less reactive due to the adjecent bridgehead in the intermediate.

Modelling Using Semi-empirical Molecular Orbital Theory

Introduction to Semi-empirical methods with comparisons draw against Molecular modelling

In the previous sections, calculations were carried out via molecular modelling which was purely based on classical mechanics. This classical method of modelling was observed to significantly deviate from experimental result as it did not take into considerations the electron interactions. Thus resulting in inaccurate results when electron density is able to play a major role in determining the progress and outcome of the chemical reaction. This failure from the molecular modelling was clearly seen in section 3 : Dimerisation of cyclopentadiene where the MM2 calculations of total minimised energy predicted the exo-product to be more stable; product of the reaction. But upon consideration of electron density and the frontier orbitals, it was rationalised that due to secondary orbital interactions the less stable endo product that was instead attained exclusively.

This brings about the importance of Semi-Empirical methods. Being semi-classical, it is able to take into account electronic behaviour by adding the valence shells s, p_x and p_y orbitals to the already present p_z orbitals from Huckel theory. The semi-empirical method that will be implemented for this section is the Hartree Fock (HF) approximation. The approximation carried out will implement a single basis function for each orbital present. This is done via the minimal basis sets known as Slater Type Orbitals(STO-3G). They are defined as the basis set for the 1s, 2s and 2p orbitals via the linear combination of 3 primitive gaussian functions. However, the minimal basis set (STO) gives rather rough results that are not accurate enough for research-quality publications; more advanced Pople-basis sets will be considered instead. Implementation of the 6-31G basis set will be considered to provide more accurate results.

The main limitations of the HF approximations is that the energy of the system calculated will always be higher than the actual energy of the real system due to the implementation of the variational theory and the independent electron approximation. Thus, the HF limit will be the smallest limiting value of the system which is almost always slightly higher than that of the actual molecule's lowest energy.

There are four main approximations made via this method of calculation that accounts form its deviation from the expected results.

• The Born-Oppenheimer Approximation

• Central Field Approximation

• Omitting Core electrons resulting in the incomplete basis set

• Absence of relativistic effects

However, despite the assumptions made which results in some deviation from the actual results, the deviations are minimal as compared to the inaccuracy attained in results via molecular modelling calculations.

Regioselective Addition of Dichlorobenzene

Dig.10 Reaction scheme for Dichlorocarbene with napthalene

9-Chloro-1,4,5,8-tetrahydro-4a,8a-methanonaphthalene undergoes a regioselective addition with dichlorocarbene (diagram 10). The starting reagent is an asymmetric molecule with the presence of two alkene bonds. This induces the potential for regioselectivity for one C=C bond over the other. The calculations carried out facilitate the rationalisations for why one C=C bond is electrophilically more favoured over the other. Based on the mechanism, electrophilic addition could either be added endo or exo to the plane. However, experimentally only the endo isomer was isolated bringing about absolute regioselectivity to the reaction.

Classical Calculation : MM2 Optimisation

|+ Table 12: MM2 Optimised energies

	(9-Chloro-1,4,5,8-tetrahydro-4a,8a-methanonaphthalene)
Image
Stretch kcal/mol	0.6218
Bend kcal/mol	4.8116
Stretch-Bend kcal/mol	0.0410
Torsion kcal/mol	7.6246
Non-1,4 VDW kcal/mol	-1.0910
1,4 VDW kcal/mol	5.7852
Dipole/Dipole kcal/mol	0.1116
Total Energy	17.9048 kcal/mol

Analysis of the JMOL (Table 12) shows that the exo-double bond has a shorter distance of 2.541 amstrongs towards the bridging carbon while the Endo-double bond distance is 2.564 amstrongs. This shows that an incoming electrophile should favourably attack the Endo-double bond instead of the Exo-double bond. Being further from the bridging carbon group, it imposes a lesser amount of sterics. This is the shortfall of the MM2 model where the interacting orbitals and electron density cannot be accounted for where only the relative sterics can be considered.

Semi-Classical Calculation : MOPAC/RM1 & mMOPAC/PM6 Semi-Empirical Optimisation

When RM1 and PM6 energy optimisations were carried out, it resulted in the total energy to be 1945.65404 eV (44867.836601 Kcal/mol). Being a different modelling method, it does not facilitate any total energy-based comparisons. Instead, comparisons of the bond distances between the Endo C=C bond (same side as the Cl bond) and Exo C=C bond is carried out.

Table 13 : Comparing the C=C bond distances

Type of Bond	MM2 model	MOPAC/RM1 model	MOPAC/PM6 model
Endo C=C bond (Angstrom)	2.564	2.504	2.543
Exo C=C bond (Angstrom)	2.541	2.492	2.539

There is a slight change in distance where the Exo bond results in a slight reduction. This could be attributed to an interaction between the C-Cl antibonding orbital and the C=C pi orbital. But this is a weak comparison as the two methods are totally different and only serves as a preliminary assumption.

Analysis of Molecular Orbitals

Dig 11 - Molecular Orbitals of 9-Chloro-1,4,5,8-tetrahydro-4a,8a-methanonaphthalene via the MOPAC/PM6

HOMO-1

HOMO

LUMO

LUMO+1

LUMO+2

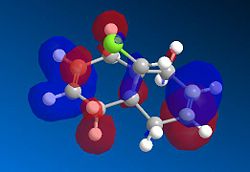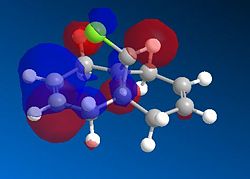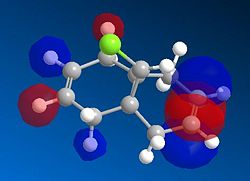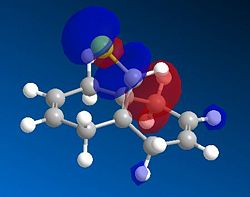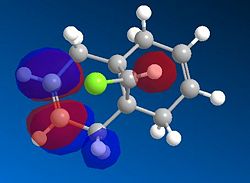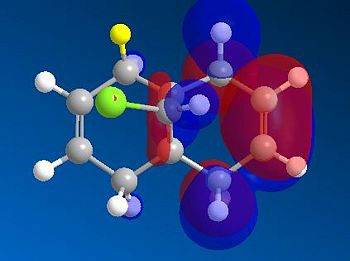
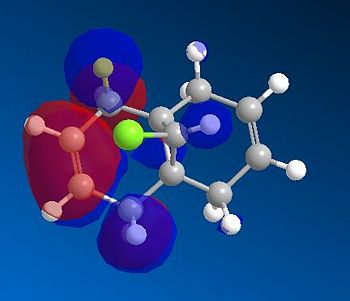
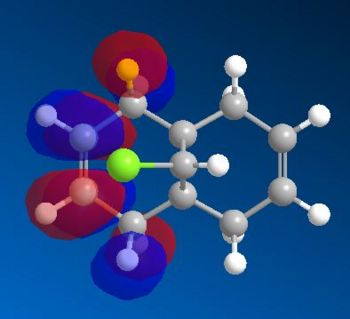
Based on the PM6 calculating model and reference to the HOMO molecular orbital, it shows that the endo-alkene has a higher electron density as compared to the exo-alkene. The exo C=C bond is defined as the alkene bond on the opposite side of the C-Cl bond (yellow). The smaller lobe size is indicative of a smaller electron density. Thus, the HOMO has the endo alkene to be more electron rich than the exo alkene. The endo alkene is more nucleophilic than the exo alkene making it more readily able to interact with the incoming electrophile as compared to the exo C=C bond. The larger lobes are indicative of sterically more accessible pi-orbitals for an electrophilic attack as compared to the exo-alkene which is sterically less accessible.

Dig. 12 Annotated electron density in the HOMO

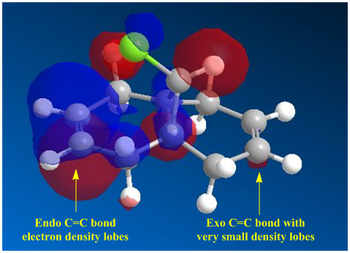
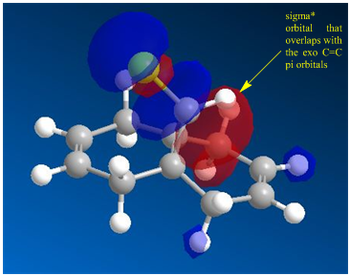
Analysis of the HOMO-1 shows that the exo orbitals are more readily stabilised as compared to the endo orbitals. This is attributed to the Cl-C sigma* orbital having an antiperiplanar interaction with the exo pi-orbital. This explains the larger lobe of the Endo alkene; indicative of higher electron density. The Cl-C sigma * orbitals are readily seen as the LUMO +1 orbitals (Diagram 13).

Diagram 13 Annotated diagrams for HOMO-1 & LUMO+1

• The above rationalisations show that endo C=C is more electrophilic and accessible to an approaching electrophile. The endo product is more readily formed as compared to the exo product. However, when this is compared with the literature molecular orbitals, deviations are seen from the above orbitals generated.

• The literature molecular orbital was ran via the MOPAC/PM3 parameters. The conformation of the molecule was bent but in diagram 12, the molecule displays plane symmetry and is flat.

• The HOMO orbitals are defined as filled Pi-orbitals while the LUMO are defined as pi* anti-bonding orbitals. But from diagram 11, it is seen that there is discrepancy where the LUMO+1 is infact sigma anti-bonding instead. This is rationalised to be due to possible orbital mixings as the C-Cl sigma* is expected to be strongly anti-bonding and a much higher energy level than LUMO+1. But mixing with a higher sigma* results in the C-Cl sigma* to be stabilised and lowered in energy to be the LUMO+1. This is highly probably due to the high degree of symmetry in the molecule since the bond lengths on both sides from the 'central carbon' is relatively equivalent (Table 13).

In efforts to minimise the discrepancy, a different calculating method was adopted to compare and contrast the molecular orbitals that resulted. This also helps to determine how detrimental the presence of the bug is in using the PM6 calculations.

Dig 14 - Molecular Orbitals of 9-Chloro-1,4,5,8-tetrahydro-4a,8a-methanonaphthalene via the MOPAC/RM1

HOMO-1

HOMO

LUMO

LUMO+1

LUMO+2

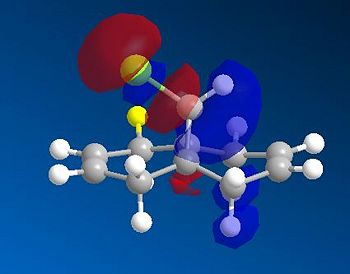Comparing and contrasting the molecular orbitals in diagram 14 against the corresponding ones in diagram 12, the following observations are made

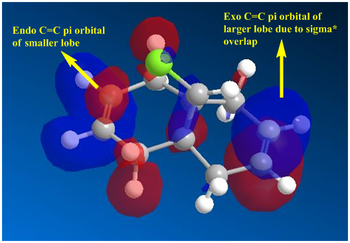
• The HOMO orbital in RM1 is similar to the HOMO orbital via the PM6. Both show that the electron density is more concentrated about the endo-alkene as compared to the exo-alkene. Thus, endo alkenes are more nucleophilic as compared to the exo alkenes. This explains why the endo product was formed under experimental conditions.

• The endo alkene region is further made nucleophilic due to the stabilisation of the exo pi-orbitals via interactions with the Cl-C sigma* antibonding oribtals. This interaction was strongly stabilising since it was of an antiperiplanar orientation; allowing maximum overlap between the orbitals. Thus, bringing about a huge extent of stabilisation for the C=C exo alkenes( Pi-->sigma*).

In conclusion, with reference to the HOMO and HOMO-1 both have considerable electron density about both the C=C bonds of the molecule. However, the endo C=C bond is of greater electron density making it more readily attacked by the electrophile. However, this does not explain the exclusive nature of the reaction as the lack of steric bulk from the top face could allow both the exo and endo C=C bonds to be attacked by the incoming electrophile. Thus, the MO diagrams are not sufficient in rationalising the regioselectivity of the molecule.

Vibrational Frequencies of the Molecules

Dig. 15 Molecules compared for the vibrational frequencies

This sections aims to vibrationally rationalise the influence the C-Cl bond has on key bond vibrations present in the molecule. The main bond vibrations to be analysed in the dialkene (A) and the monoalkene (B) are the (i) C-Cl bond stretches (ii)Endo C=C bond stretches (iii) Exo C=C bond stretches. The smaller the vibrational wavenumber the weaker bond.

The calculations for the bond energies were carried out in the following specific steps to result in the respective sections below.

1. The molecular structures were optimised by the use of the MM2 force field parameters (Classical)

2. The MOPAC/PM6 energy minimisations were carried out (Semi-classical)

3. The structures were then exported to Gaussview where they were subjected to B3LYP / 6-31 G(d,p) geometric optimisation and successive vibrational frequency calculation

Dialkene vibrational frequencies analysis

The approach taken towards this analysis was to analyse the IR spectra by focusing on the key stretches initially highlighted. Then the stretches, magnitude and its intensity were tabulated in Table 14.

Dig. 16 Infrared Spectrum of the Dialkene molecule with specific bond stretches annotated

Table 14 : The different Bond stretching vibrations and their vibrational wave numbers

Type of Vibration	Image with arrows	Vibrational wavenumber (cm-1)	Intensity	Energy (kJmol-1)
C-Cl stretch		770.921	25.115	9.22
exo C=C stretch		1737.14	4.2078	20.79
endo C=C stretch		1757.37	3.9338	21.02

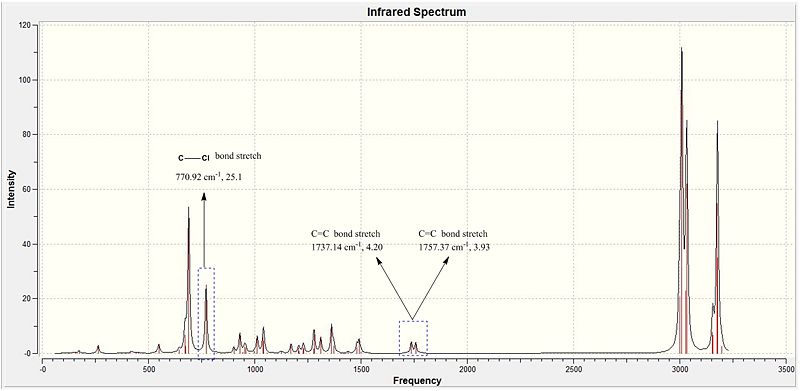
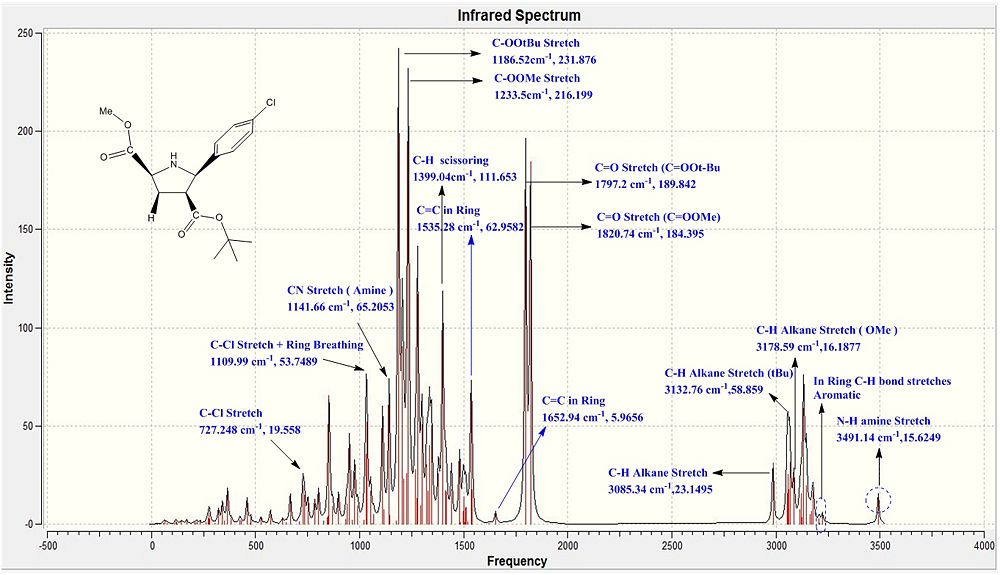
Analysis of Table 14 and the corresponding Ir spectra in diagram 16 shows the 3 key peaks indicative of the dialkene. The C=C bond stretches are seen as two seperate peaks as they are in chemically inequivalent environments so the bond stretch of the endo C=C bond is not equivalent to that of the exo C=C bond. There is significant difference in the electron density of the two C=C bonds (This was established in the earlier MO section). The literature Stretching frequency for C-Cl stretches is 780 cm^-1 which is very close to the experimentally attained value of 770.921 cm^-1. Thus, the C-Cl bond is proven to be present via IR methods.

Similarly, C=C bond stretches has a literature value of 1670-1870 cm^-1. Both values in table 14 are within the range. However, the Exo has a smaller stretching frequency magnitude as compared to the endo C=C bond. This can be re-considered with the conclusion made in the earlier MO section. The C-Cl bond is anti-periplaner to the exo C=C pi orbitals allowing an effective overlap of the C-Cl sigma* antibonding orbitals with the C=C exo pi bonding orbitals. Thus, there will be a significant amount of electron density from the C=C bond directed towards the sigma* bond. But C=C endo is not antiperiplanar to the C-Cl orbital and will not have this secondary orbital interactions. Thus, the electron density of the C=C endo is larger than the C=C exo allowing the endo to have a greater vibrational frequency and thus a slightly higher magnitude by +20 cm^-1.

Monoalkene vibrational frequencies analysis

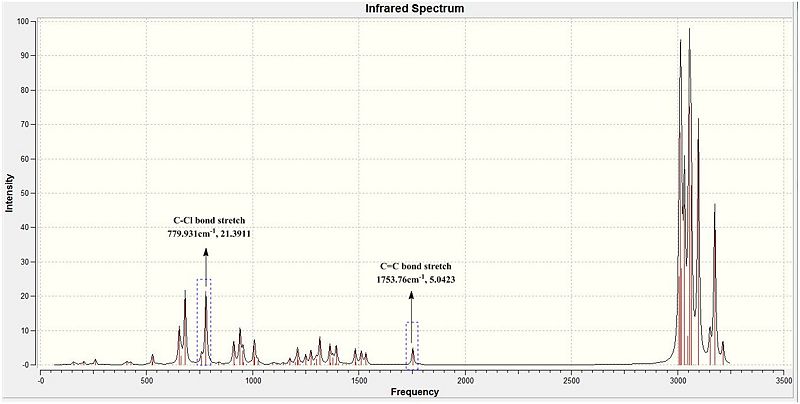
A similar approach taken towards this analysis by focusing on the key stretches initially highlighted. The stretches, magnitude and its intensity were tabulated in Table 15. This will allow easier comparisons to be made between this section and the previous one; facilitating conclusions to be drawn.

Dig. 17 Infrared Spectrum of the Dialkene molecule with specific bond stretches annotated

Table 14 : The different Bond stretching vibrations and their vibrational wave numbers

Type of Vibration	Image with arrows	Vibrational wavenumber (cm-1)	Intensity	Energy (kJmol-1)
C-Cl stretch		779.931	21.3911	9.35
endo C=C stretch		1753.76	5.0423	21.11

Conclusions Drawn from vibrational Analysis

The C-Cl vibrational stretch according to literature is defined as a strong sharp peak at 780 cm^-1. When this value is compared with those of (A) and (B), it is concluded that they are in good agreement with literature.

Molecule (A) which is the dialkene, has two asymmetric alkenes which have slightly different C=C bond stretches. The Endo C=C bond has a vibrational frequency of 1757 cm^-1 while the Exo C=C bond have a vibrational stretch of 1737 cm^-1. But molecule (B) having only 1 C=C bond (Endo) would have only 1 value expected and indeed only 1 peak was seen in the IR 1753.76 cm^-1. Both the Endo stretches are of a similar value (in bold) indicative that they are in rather similar environments and have minimal influence to the C=C electron density due to the hydrogenation of the exo C=C bond. However, in general when compared with literature (1670-1870 cm^-1) it is noticed that both molecules have the C=C bonds to be of a slightly greater energy level. This is indicative of strong bonds which could be due to possible orbital mixings that further stabilises the pi bonds and hence account for the slightly higher C=C bond magnitude.

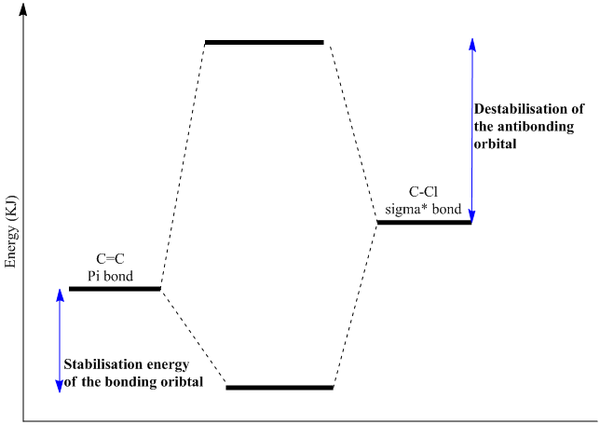
Another reason could be attributed to the earlier conclusions drawn in the Molecular orbital analysis where it was concluded that the C-Cl sigma* has an anti periplanar overlap with the Pi orbitals of the exo C=C bond. This will allow the overlap to be strong and so greater stabilisation of the bonding orbital (Pi orbital of the Exo C=C bond). The lowering of the orbital makes it a stronger more stable bond which is indicated by a higher magnitude vibrational frequency. (Diagram 18 ) This stabilisation will only be seen in (A) where there is the availability of the C=C exo. But in (B), the absence of the C=C exo will not allow this secondary stabilisation to be present.

Dig.18 MO diagram showing the Stabilisation of the Exo C=C pi bond

Additional Exercise

This exercise investigates the influence a substituent on the Exo-alkene has towards the bond strengths of the three key bonds considered in the earlier sections (i) C-Cl bond stretch (ii) Endo C=C bond stretch and (iii) Exo-bond stretch. This was done by varying between 4 different substituents that were made up of two distinct nature. The first type were electropositive substituents namely SiH₃ and BH₂. The second group of substituents were electronegative substituents namely the OH and CN. Thus, the electron donating and electron withdrawing influences brought about by the respective substituents were investigated by measuring the respective stretching frequencies as mentioned to allow a compare and contrast to be carried out. Diagram 19 shows the four different substituents considered and the sub-groups they fall under.

Dig. 19 Summary of the Different substituents considered

Table 15: Summarising the different molecules and the influence upon the C=C and C-Cl bonds

R Substituent	Nature of substituent	Image	Jmol	MM2 Optimisation (Kcal/mol)	Endo C=C stretch cm-1	Exo C=C stretch cm-1	C-Cl stretch cm-1
SiH3	Electropositive			17.6081	1756.22	1689.57	761.73
BH2	Electropositive			15.8271	1756.56	1657.2	759.042
OH	Electronegative			17.9484	1756.27	1776.6	766.786
CN	Electronegative			16.7286	1756.54	1706.31	765.79

When an electropositive R group is introduced as the exo-substituent such as BH₂ substituent or the SiH₃ they are able to influence the different bonds in the molecule electronically. Being electropositive groups they were electron-donating groups by nature and resulting in readily donating electron density towards the C=C pi orbitals of the ring. This allowed the antiperiplanar orbital overlap with the C-Cl sigma* orbitals to become more significant. As the sigma* oribtal became more stronger it leads to the C-Cl bond to become weaker as the antibonding orbital is more readily occupied. This is seen in the vibrational frequency of the C-Cl bond which by literature should boe 780 cm^-1. But due to the increased Pi-->Sigma* interaction the stretching when R=SiH₃ is reduced to 761.73 cm^-1 and in BH₂ 759.042 cm^-1. Similarly as the C=C exo has the electron density directed towards the interaction with the C-Cl sigma* orbital, the C=C bond also becomes less electron dense and is also expected to have a lower than literature stretching frequency. This was also observed as predicted where the C=C exo bond frequency i SiH₃ is reduced to 1689.57 cm^-1 and in BH₂ 1657.2 cm^-1. This was significantly lower than the endo C=C bonds which was part of the same molecule but did not have the antiperiplanar interactions with the C-Cl antibonding oribtals. This allowed the endo C=C bonds to be of greater electron density and so a higher magnitude vibrational frequency.

In contrast when an electronegative R group is introduced as the exo-substituent such as OH or CN, they are able to influence the different bonds within the molecule electronically. The electronegative groups being electron-withdrawing would make the C=C exo bond less electron dense as compared to the endo C=C bond. The reduction in the pi orbitals electron density would mean the pi orbital are not readily able to have secondary orbital overlaps with the C-Cl antibonding orbital as readily. As the antibonding interaction becomes weaker, the C-Cl sigma bond is stronger and would have a higher magnitude for the vibrational frequency which is determined to be 766.786 cm^-1 when R=OH and 765.79 cm^-1 when R=CN which is much closer to the literature value of 780 cm^-1 as compared to the other two substituents. When the C=C bond vibrational frequency is analysed, it is seen that down the table the magnitude of the exo C=C bond becomes more closer to that of the endo since it is less readily available to functinon as a electron donating orbital and instead functions as double bond with no secondary orbital interactions as it does not have sufficient electron density for such interactions. However due to the inductive effect it is still slightly weaker in bond strength as compared to the endo C=C bonds. Thus, the endo C=C when R=OH or CN is of a slightly higher magnitude than the exo C=C bond.

Structure based Mini Project Using DFT-based Molecular Orbital methods

The purpose of the mini project was to implement the different modelling techniques adopted in the previous sections towards organic reactions that give rise to a mixture of different isomers. The different modelling techniques would ideally, be able to rationalise the reaction carried out where it should be able to provide sufficient conclusions to justify the formation of the isomers and possibly lead to determining the ideal conditions where one isomer could dominate and be isolated for further reactions. This plays a key role in stereospecific/regiospecific reactions where the wrong isomer formed could result in the expected chemical reaction to not occur. This could be translated to a biological effect if the wrong isomer of a drug is administered resulting in adverse reactions. Thus, computational chemistry serves as a tool in accurately identifying the specific isomers in a mixture.

Introduction to the Mini-Project: Cu(I)-Catalyzed Highly Exo-selective and Enantioselective [3 + 2] Cycloaddition of Azomethine Ylides with Acrylates

This reaction has been chosen as it involves the formation of highly substituted 5-membered heterocycles via a very common 1,3-Dipolar cycloaddition method. The 5 membered rings being highly substituted, are very useful towards the synthesis of biologically active molecules and functioning as organic catalysts. Thus, it is of paramount importance that the correct isomer is isolated for its further use in the synthesis of catalysts and biological molecules. In most cycloaddition reactions that involves the combination of N-methalated azomethine yildes and electron deficient alkenes, the endo adduct was either the major product or it was the absolute product formed. In this paper however, the Cu-(I)/P,N-ligand catalyzed [3 + 2] cycloaddition of N-metalated azomethine ylides with acrylates was able to yield the exo adduct as the major product with high enantioselectivity. Furthermore, the studies carried out were the first to have use the Cu(I) salt as a catalyst towards 1,3-Dipolar cycloaddition of azomethine ylides.

Diagram A- Reaction scheme for Cu(I)-Catalyzed 1,3-Dipolar Cycloaddition

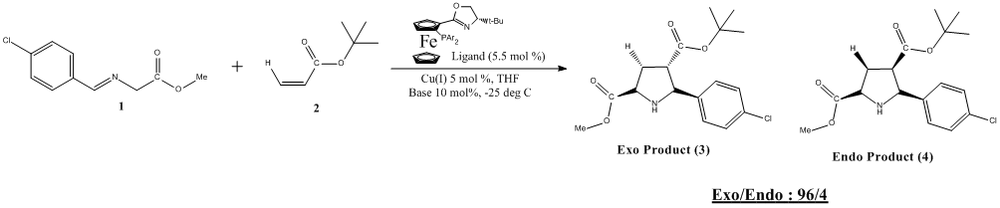
The reaction is a novel Cu(I)/P,N-ligand catalyzed asymmetric 1,3-dipolar cycloaddition of azomethine ylides with acrylates, providing exo products of polysubstituted proline derivatives in up to 98% enantiomeric excess.

Purpose of Computational Efforts

The 1,3 Dipolar cycloadditions cycloaddition reaction having said to be a novel reaction drew my interest. Thus, computational techniques are employed to validate the authenticity of the results published and inevitably determine the reliability of the results and the findings made towards 1,3 Dipolar cycloadditions. This will be quantitatively carried out by comparing the calculated ¹³C NMR against the literature. Similarly the same method will be carried out with the less accurate ¹H NMR spectra as well.

The typical cycloaddition usually yields the endo product as the major or only product in previous reactions and could be justified due to favourable secondary stabilisations present. But in this reaction the exo was the significant majority of 96%. Thus, the individual energies of the endo and exo isomers are to be determined to rule out thermodynamic control. Also, the possible influence of any secondary stabilisations is to be looked into; in-efforts to rationalise why the exo is favoured over the endo product.

Underlying Mechanism

Diagram (B)- Proposed reaction mechanism towards the absolute synthesis of the Exo-product (Adapted from literature source)

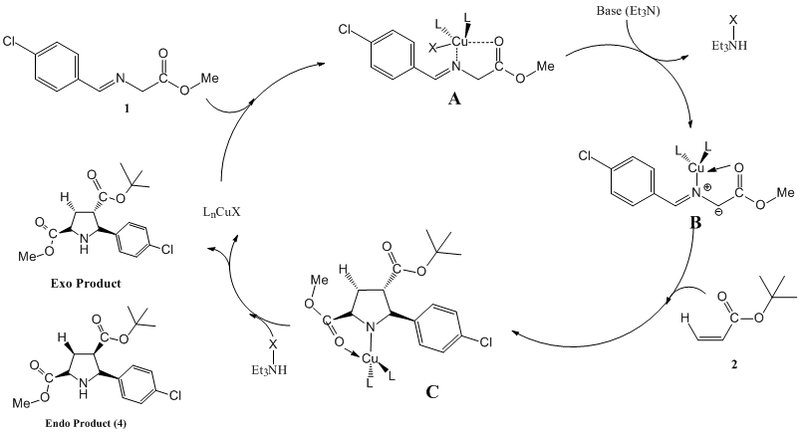
With reference to Dig. B, the first step involves the formation of complex A via the complexation of the Imine (1) to the copper(I) catalyst. The Copper(I) is able to have interactions with both the N and O hetero atoms to form the complex.

The addition of the base triethylamine facilitates deprotonation of the alpha proton which is highly acidic due to being in-between two electron withdrawing groups. This allows the formation of the highly reactive azomethine ylide-Copper(I) complex B.

The reactive species formed is able to react with different dipolarphiles to facilitate the formation of intermediate C. Upon interaction with the ammonium salt formed upon proton abstraction, the copper catalyst and base are regenerated. The exo is formed as the major product while the endo is formed as the minor in a ratio of 96:4.

Mechanistic Rationalisation

Based on the mechanism, a preliminary rationale for the selectivity of the exo over the endo can be made. The intermediate B (Diagram B), has the transition metal centre forming the isolable complex. The copper(I) metal from group 11 has a +1 oxidative charge making have a d¹⁰orbital configuration. Thus, it can have a tetrahedral coordination with four bulky L-type ligands to achieve the stable 18 electron complex. The interaction with the carbonyl (O) and the Imine (N) allows this stable electron configuration to be achieved.

Phosphino-Oxazoline ligands were used for coordination to the Cu(I) centred complex, these in combination with Cu(OAc) were readily able to catalyse the [3+2] cycloaddition. They were also determined to bring about strong exo-selectivity over the endo product. This was because the large bulky ligands added on to the steric bulk around the metal complex (Diagram C). This made the steric repulsion between the ligands and the dipolarophiles to become more significant and thus the endo approach was highly not favoured. The exo approach minimised the steric repulsion making it much more favourable.

Diagram C- Significant steric clash present in the formation of the endo as compared to exo

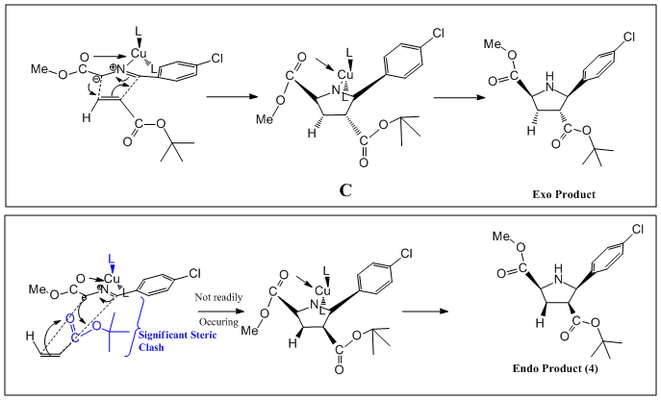
Rationalising the issue of Selectivity via modelling programmes

The following section will look to prove the conclusions drawn from the mechanisatic analysis carried out. The minimial energy of the 2 possible products will be attained and compared to determine if there is any thermodynamic control for the dominance of the exo over the endo isomer. Following that the respective IR and NMR spectra will be analysed and compared with the literature values to determine the accuracy of the literature.

Conformational Analysis of Considered Isomers

Table A: MM2 Optimised and PM6 Optimised energies

	Exo Product	Endo Product
Image upon MM2 optimisation
Stretch kcal/mol	1.5834	1.6641
Bend kcal/mol	7.8428	8.2561
Stretch-Bend kcal/mol	0.4767	0.5462
Torsion kcal/mol	-3.9131	-1.6198
Non-1,4 VDW kcal/mol	-7.1173	-7.6094
1,4 VDW kcal/mol	17.6254	18.0415
Dipole/Dipole kcal/mol	4.2308	4.2522
Selected Dihedral Angle via MM2 (deg)	-85	34
Total Energy (MM2)	20.8285 kcal/mol	23.5309 kcal/mol
Selected Dihedral Angle via PM6 (deg)	-101	6
Image Upon Optimisation (PM6)
Heat of Formation (PM6)	-187.60199 kcal/mol	-182.01345 Kcal/Mol
Heat of Formation (DFT-631(d,p))	-1476.71913280 a.u.	-1476.74522110 a.u.

Both the endo and exo products were optimised under the MM2 parameters (classical), The PM6 semi-classical parameters and finally the DFT (quantum) parameters. All three modes of calculations could not be inter-related as they were of different modes. But the difference in energy between the endo and the exo across all three systems brought about the same conclusion. Both products had realtively similar energy levels such as in the DFT where they only differed by a 0.03 a.u. difference from each other. The DFT optimisation could be carried out as it only too 45 mins for the geometry optimisation which was relatively short.

This allows the conclusion to be made that the reason for the exo to be preferred over the endo is not due to thermodynamic control as they are both of relatively similar energy if formed. Thus it should be a non-thermodynamic reason that reasons in the exclusive formation of the exo instead of the endo. Comparing the Jmol for the PM6 against the MM2 would show that they were of relatively similar orientations w.r.t dihedral angles thus should that the optimum starting point was chosen for the mm2 modelling.

NMR comparisons

¹H NMR DOI:10.1021/ol0516925

Literature ¹H NMR for Exo product

From the Literature paper under study, the ¹H NMR for the Exo product is given as 1H NMR (360MHz, CDCl3) δ 7.39 (d, J = 8.5 Hz, 2 H), 7.28 (d, J = 8.5 Hz, 2 H), 4.31 (d, J = 8.6 Hz, 1H), 4.00 (dd, J = 8.8 and 5.3 Hz, 1 H), 3.76 (s, 3 H), 2.74 (q, J = 8.8 Hz, 1 H), 2.45 (dt, J= 13.0 and 8.8 Hz, 1 H), 2.35-2.25 (m, 2 H), 1.35 (s, 9 H).

Calculated ¹H NMR for the Exo product DOI:10042/to-7346

Diagram D- representing calculated H NMR peaks for Exo product

Comparisons made for the Calculated Against the Literature value

Diagram E- for Numbered Hydrogens

Table B- representing calculated against Literature values

Graph A- for Calculated Vs Literature Chemical Shifts

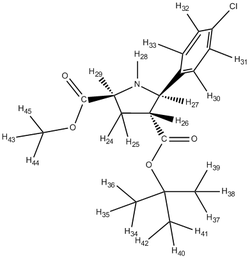
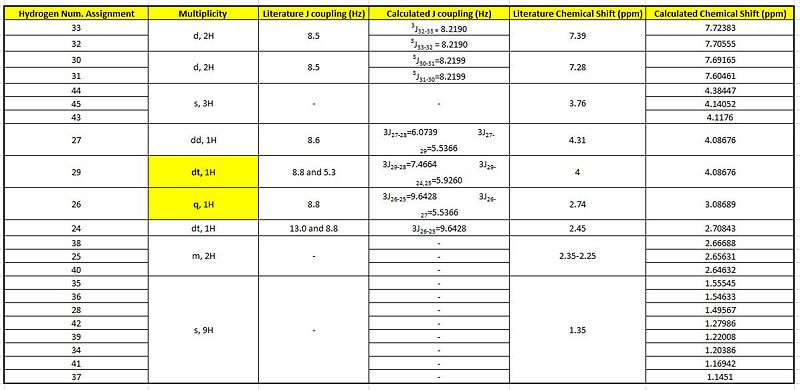
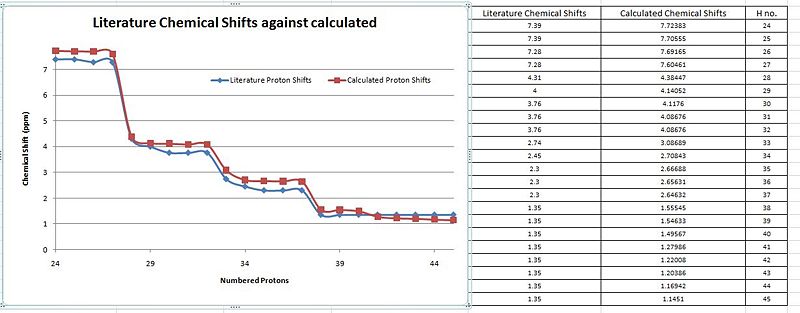
Although, it was stated that the ¹H NMR were less reliable, the ³J_H-H coupling constants were compared with the literature attained coupling constants. This was done by the utility of the Jancchio software to provide the computationally calculated coupling constants. The results were summarised in table B along with the calculated chemical shifts 'tagged' onto the proton expected of that chemical shift.

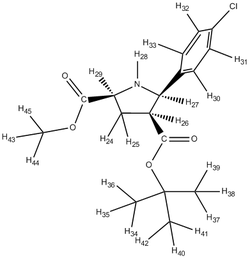
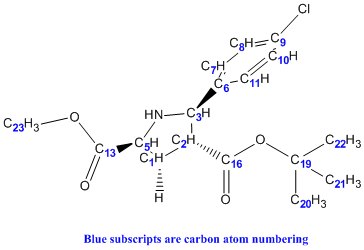
It was noticed that literature did not 'label' the protons corresponding to the different chemical shifts so this was done to allow better rationalisation of the spectra. For eg. the identification of H-27 being more deshielded than H-28 could have be mistaken as the opposite since H-28 is bonded to the electron-withdrawing N heteroatom.

When a comparison of the literature chemical shifts are done against the calculated chemical shifts (Graph A),there are slight deviations in the overall alighnment of the plots. This slight deviations is indicative of significantly small differences between the calculated and literature values. From the table, it is noticed that computationally, a chemical shift is assigned for every proton even if they are in the same chemical environment unlike in literature which has a lesser. This is because, in the computational 'environment' the molecule is frozen with the protons in their specific positions. Thus the protons of a methyl functional group will be seen as being in different but similar chemical environments. But in the actual NMR carried out, the molecules are free to rotate about the sigma bonds and thus there will be chemically equivalent environments present such as the methyl or the t-butyl which has all 9 protons in the same chemical environment and presented by a single peak of an integration of 9. As both the molecules are sterochemically different from each other, they are expected to have relatively similar chemical shifts by the different functional groups.

Thus, the calculated spectra is in good correlation with the computationally calculated values for the Exo H nmr.

Literature ¹H NMR for Endo product

From the Literature paper under study, the ¹H NMR for the Endo product is given as 1H NMR (360 MHz, CDCl3) δ 7.35-7.25 (m, 4 H), 4.44 (d, J = 7.8 Hz, 1 H), 3.94 (t,J = 8.2 Hz, 1 H), 3.80 (s, 3 H), 3.24 (q, J = 7.8 Hz, 1 H), 2.55 (br, 1 H), 2.43 (dt, J = 13.3 4 and 8.2 Hz, 1 H), 2.35-2.25 (m, 1 H), 1.06 (s, 9 H)

Calculated ¹H NMR for the Endo product DOI:10042/to-7343

Diagram F representing calculated ¹H NMR peaks for Endo product

Comparisons made for the Calculated Against the Literature value

Diagram G for Numbered Hydrogens

Table C representing calculated against Literature values

Graph B for Calculated Vs Literature Chemical Shifts

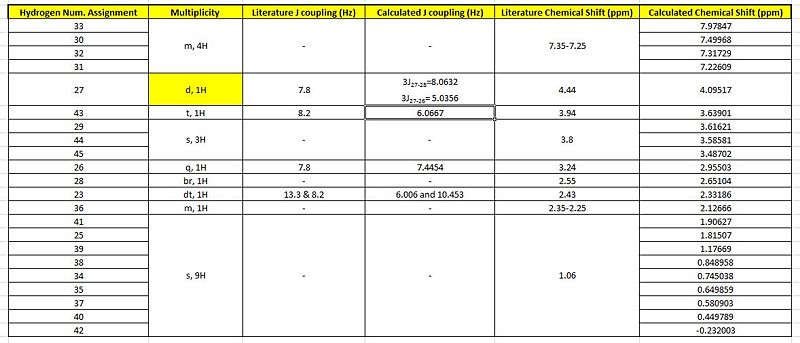
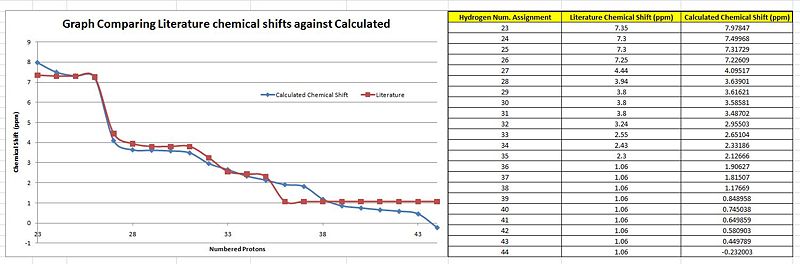
Similar to the exo case the less number of peaks seen in the literature values as compared to the computational would be due to the computing method looking at the molecule in a 'frozen' state where rotations about the c-c bonds are not considered. However, for the endo H nmr comparisons there is a less 'fit' of the 2 plots indicative of a more significant deviation from the literature values. This could be seen at H-42 which computationally is a -0.23ppm chemical shift while literature is of 1.06 ppm. This would be the draw back as by theory, the last 9 protons in the table should be chemically equivalent and have the same chemical shift.

But overall the graphs do have a significant number of plots to correspond to each other well with minimal deviations making it relatively accurate.

¹³C NMR

Literature ¹³C NMR for Exo product

13C NMR (90 MHz, CDCl3) δ 175.0, 172.6, 140.7, 133.7, 129.0, 128.8, 81.5, 66.4, 59.5, 52.8, 52.6, 34.5, 28.4;

Calculated ¹³C NMR for the Exo product DOI:10042/to-7346

Diagram H representing calculated 13C NMR peaks for Exo product

Comparisons made for the Calculated Against the Literature value

Diagram I for Numbered Carbons

Table D representing calculated against Literature values

Graph C for Calculated Vs Literature Chemical Shifts

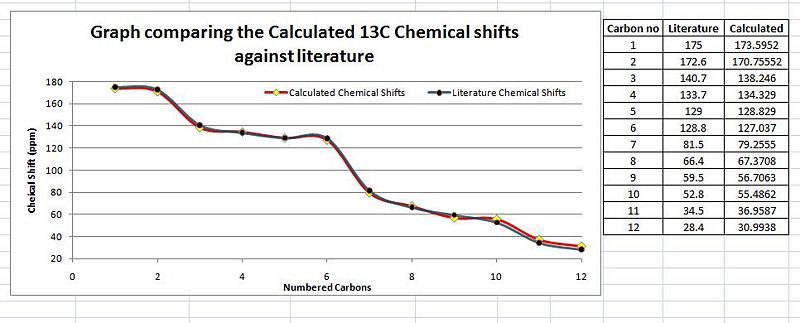
As the carbons are all accounted for individually via both the literature and computationally, unlike in the H NMR analysis, here the total number of data points correspond to each other. However, as the position of the different carbons influences the extent of deshielding and this is to be taken into account a number of error corrections are carried out. These error corrections as labelled in the table above show a much greater similarity to the literature values which makes the 13C NMR much more accurate as compared to the H nmr. This is well observed by the plot of the graph where there is a large degree of overlap between the two plots. This is indicative of very minimal deviations for the calculated from the literature chemical shifts. This is quantitatively seen where all the differences are less than 3 ppm.

Thus the correlation for the exo product is good and can be concluded that the exo-product has indeed been attained as stated in literature.

Literature ¹³C NMR for Endo product

13C NMR (90 MHz, CDCl3) δ 174.0, 171.9, 138.5, 133.5, 129.1, 128.6, 81.2, 65.2, 60.2, 52.6, 50.5, 34.2, 27.9

Calculated ¹³C NMR for the Endo product DOI:10042/to-7343

Diagram J representing calculated 13C NMR peaks for Endo product

Comparisons made for the Calculated Against the Literature value

Diagram K for Numbered Carbond

Table E representing calculated against Literature values

Graph L for Calculated Vs Literature Chemical Shifts

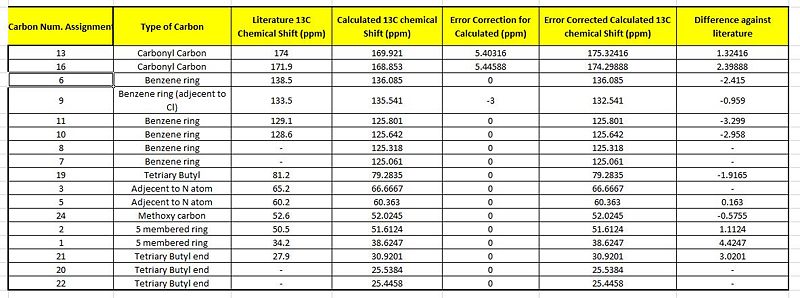
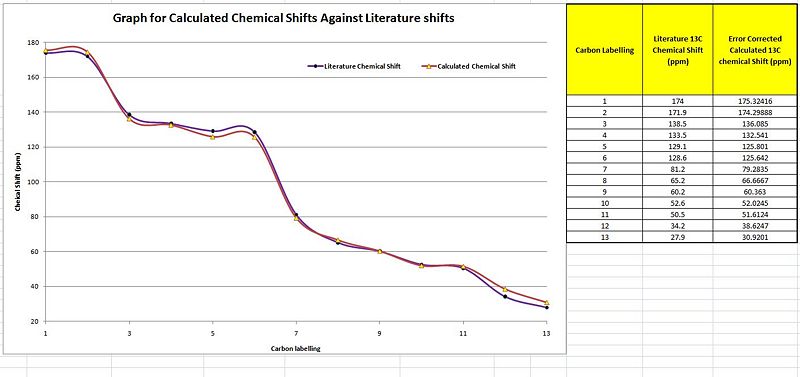
On the exact points as for the exo 13C NMR, the correct product has been formed due to the almost perfect overlap of the two plots with only 1 data point to be over the 3 ppm difference. Thus it can be concluded that the correct endo product has been formed in literature as well.

Conclusions Drawn

The 13C NMR is indeed more accurate in comparing against the literature chemical shifts as seen by the degree of overlap between the plots in the respective graphs. From both the 13C plots that compared with the literature paper, it is conclusively said that the correct products have been isolated and formed as reported. However, there was some deviation in the calculated values from that of the literature. The reasons have been summarised as below

The computational method observes the molecule from a 'frozen' view; the conformation the molecule is in is the conformation in which it is analysed. This could differ from reality where in reality where not bound by potential energy wells, it would indeed adopt the lowest energy conformation whereas in the computer form it could have adopted a pseudo-lowest energy due to being trapped by an energy well as in the case of the MM2 optimisation.

In the computational model the influence the solvent (CDCl3) is not taken into account if it has an influence in the conformation. Thus it can be expected that the real conformation will deviate slightly from that modelled in the computer. Thus the error in determining the lowest energy conformation despite using the DFT method could have led to the slight deviations seen in the tables above.

A significant amount of difficultly was faced in assigning the chemical shifts to the contributing protons against literature chemical shifts. This is expected to be due to the resoultion power of the NMR machine. If it is at low resolution, the expected peaks of slightly different chemical shifts will be seen as a single overlapping peak or as a multiplet that will be hard to distinguish. Thus explain why the expected quartet via computational modelling is only seen as a double or a triplet as the very small coupling constants result in the peaks to be seen as one.

IR Analysis

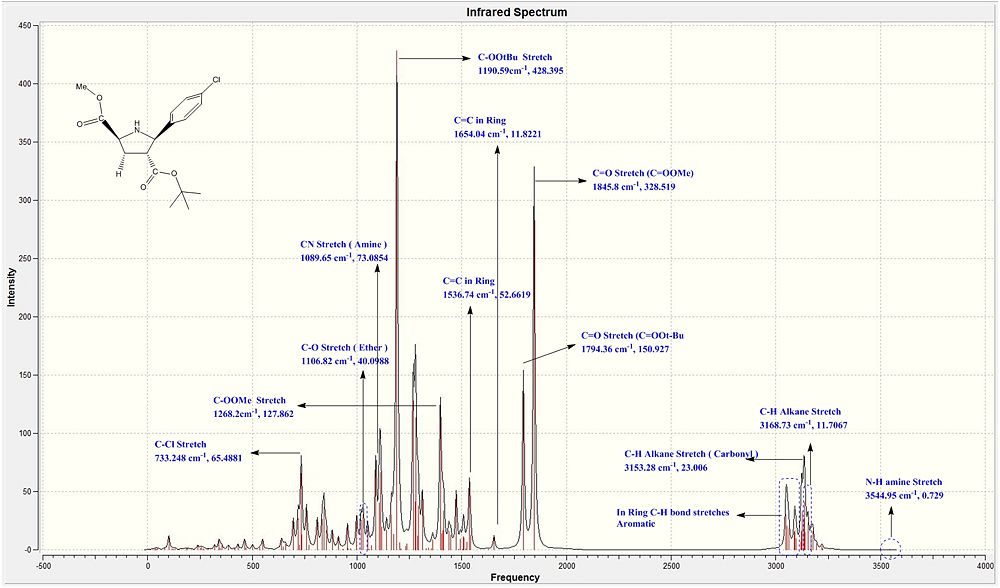
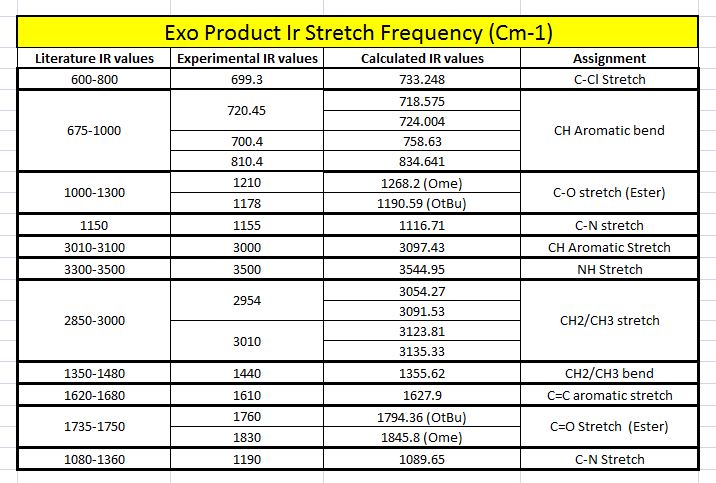
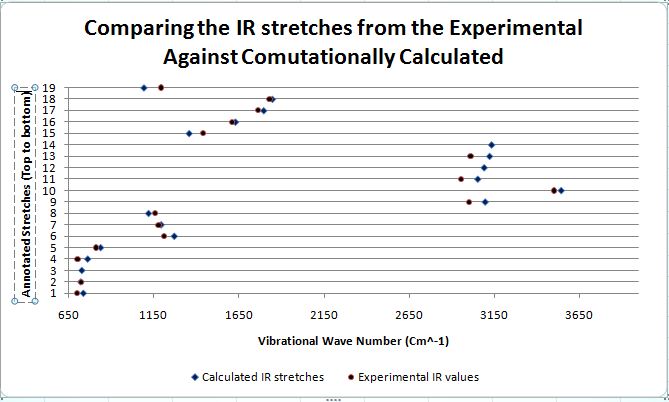
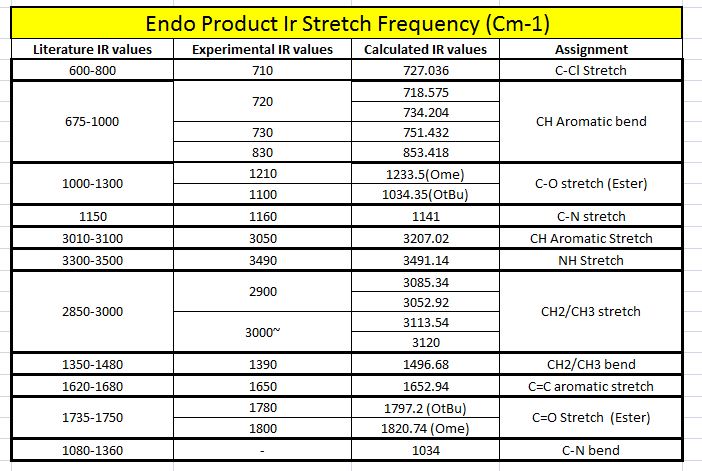
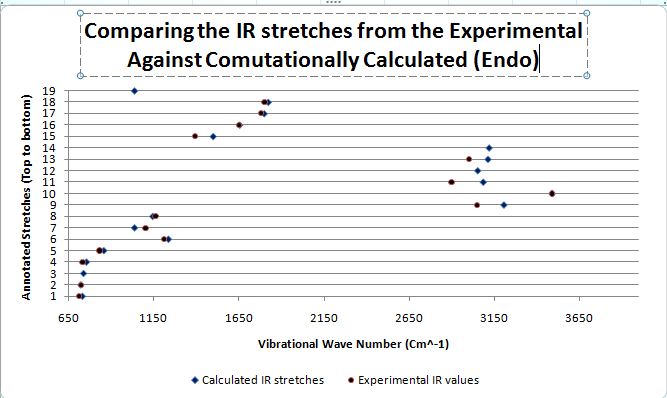
Both the literature IR values were taken from the exact literature source as for the NMR section. For the computationally calculated IR values, they were attained by first carrying out both the MM2 and PM6 energy minimisations. Following that, the DFT gaussian calculations were carried out to optimise the geometry for more accurate vibrational frequencies to be acquired. The B3LYP model with the 6-31G(d,p) basis set was used both the exo and endo ir calculations.

IR comparison with Literature for the Exo Product

Diagram M Annotated IR spectra for the Exo Product

Diagram Table F comparing the calculated stretches against literature

Graph E comparing Experimental against Calculated

Dig N - Annotated diagrams of the key bond stretches

C-Cl stretch

C=C in ring stretch

C=O OMe stretch

C=O Ot-Bu stretch

C-H Alkane stretch

C-O Ester stretch

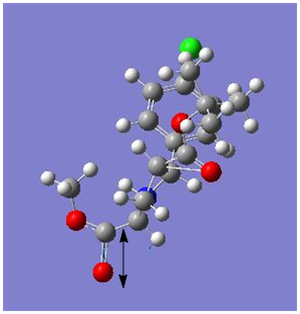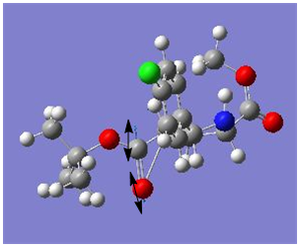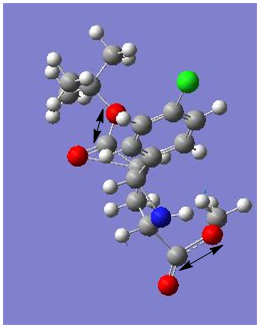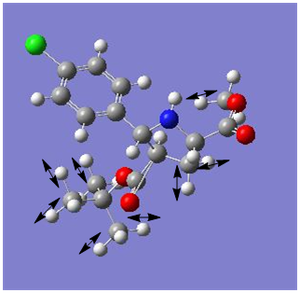
IR comparison with Literature for the Endo Product

Diagram O Annotated IR spectra for the Endo Product

Table F comparing the calculated stretches against literature

Graph comparing the calculated results against the experimental

Dig P - Annotated diagrams of the key bond stretches

C-Cl stretch

C=C in ring stretch

C=O OMe stretch

C=O Ot-Bu stretch

C-O Ester (Ot-Bu stretch

C-O Ester (OMe) stretch

CN stretch

Conclusions Drawn

When both the Ir spectras, corresponding table and graphs were compared, it is seen that the IR stretching frequencies for both the molecules are almost identical. Both the calculated IR spectra encompassed the key vibrations that were expected from the molecule such as the N-H, and the 2 distinct carbonyl stretches. The stretching frequency of the methoxy carbonyl C=O stretch is slightly higher than the stretching frequency of the O-tBu C=O stretching in both the compounds which is indicative that there is a slightly stronger C=O bond in the methoxy carbonyl as compared to the O-tBu. But as both are very similar with minimal deviations from the literature range, the computational geometry of the two products can be said to be rather accurate to that of the molecule in reality.

Overall Conclusion Drawn

In conclusion, the NMR assignment attained computationally correlate well to the literature ¹H and ¹³C NMR spectras. Furthermore, comparisons made via the IR spectras show equally good correspondence with literature IR values. However as rationalised earlier, there is large similarity is both the exo and endo ¹³C chemical shifts. This would suggest that another method is required besides NMR and IR to differentiate the two compounds from each other. The separation of the enatiomers could readily take place via the use of CaSH which gave a literature yield of in ratio of 1.5:1 for exo:endo products. Also physical methods such as chiral chromatography could be considered for the complete isolation of the 2 compounds in the 96:4 ratio of the exo:endo with the exo in 97% ee excess.

IceBurn 16:13, 1 March 2011 (UTC)