Sn3215y2

Introduction

In analyzing reaction kinetics, one method is the consideration of potential energy surfaces. In simple systems, it is possible to approximate the potential surface with electrostatic interactions between atoms and molecules. Reaction pathways can then be clearly predicted by applying a set of initial conditions to the surface.

In this experiment, we analyze two simple systems: System A consists of three hydrogen atoms, and system B consists of two hydrogen atoms and one fluorine atom. The features of both potential energy surfaces are described (eg. the transition state), and the outcomes of different sets of initial conditions are analyzed. Finally, system B is used to illustrate Polanyi's empirical rules, which define the relative efficiency of translational and vibrational energy in early- and late-barrier systems with respect to inciting a reaction

System A: H-H-H

Question 1: What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.

- At minima and transition states, the total gradient of the potential energy surface is zero. Minima can be interpreted as stable equilibria, and transition states can be interpreted as unstable equilibria. Therefore, particles displaced a small amount from a minimum will tend to return to the minimum, whereas particles displaced from a transition state will tend to move away from the transition state towards the products or reactants.

(Fv611 (talk) 14:48, 17 May 2017 (BST) Correct, but you do not relate your answer to the curvature of the surface.)

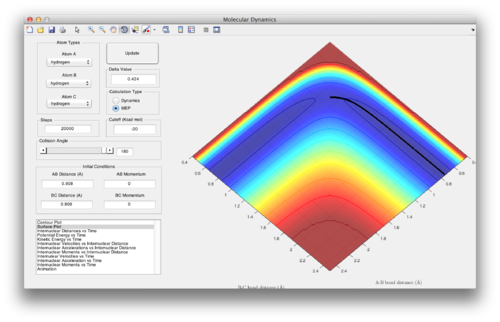
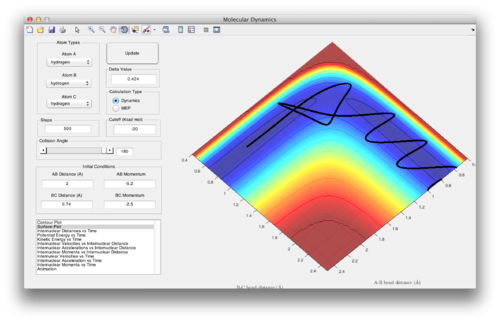
Question 2: Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” screenshot for a relevant trajectory.

-

rts = 0.908Å. At the transition state, the gradient of the potential energy surface is zero, ie. there is no force acting on the system. If the particles are initiated with zero momentum, there should be no changes in the internuclear distance as time passes, as no forces are acting on the particles. The screenshot for internuclear distance vs time at r12= 0.908Å shows that the internuclear distances are constant, indicating that r12=0.908Å is the transition state.

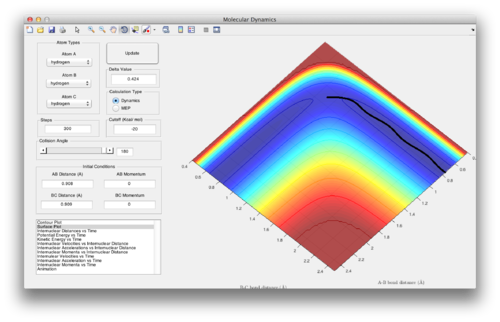
Question 3: Comment on how the mep and the trajectory you just calculated differ. The mep shows the systems moving into the valley and continuing on in a straight line, whereas the dynamics simulations shows the system oscillating as it moves through the valley, due to the inertia gained from descending from the transition state.

Setup a calculation where the initial positions correspond to the final positions of the trajectory you calculated above, the same final momenta values but with their signs reversed: AB = 0.7264 Å, BC =2 Å, AB momentum = -1.236, BC momentum = -2.486. BC decreases until BC forms an atom and AB breaks with A moving off to infinity.

(Fv611 (talk) 14:48, 17 May 2017 (BST) Why does it gain inertia in the dynamic simulation and not in the mep?)

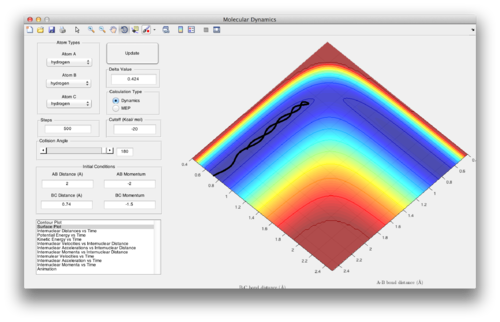
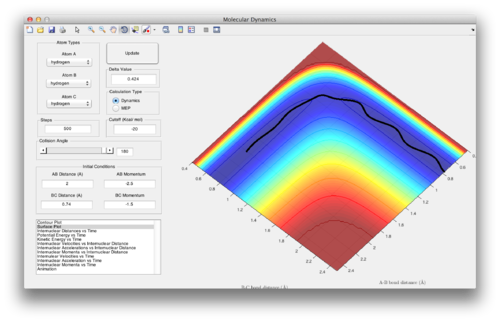
Question 4: Complete the table by adding a column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a screenshot of the trajectory and a small description for what happens along the trajectory.

p1	p2	Reactivity
-1.25	-2.5	Reactive
-1.5	-2.0	Unreactive
-1.5	-2.5	Reactive
-2.5	-5.0	Unreactive
-2.5	-5.2	Reactive

1. The system progresses smoothly through the transition state to form AB.

2. The system does not have enough energy to reach the transition state, instead reverting back to BC.

3. The system progresses smoothly through the transition state to form AB.

4. Barrier recrossing: The system progresses through the transition state and initially forms AB, but then reverts back to BC.

5. The system bounces between AB and BC before forming AB in the end.

(Fv611 (talk) 14:48, 17 May 2017 (BST) Correctly identified the reactive trajectories, but you provided no physical explanation of what's happening) Question 5: State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

Transition state theory assumes that atoms and molecules behave classically (ignoring quantum effects), and that the behavior of atoms in a system can be modelled by a potential energy surface. In addition to energetic barriers, transition state theory is capable of accounting for the role of vibrational modes in a reaction. As transition state theory operates on the properties of thermodynamics (ie. based on macroscale interactions, eg. kinetic energy), the results of transition state theory should predict experimental results fairly accurately for large-scale reactions in the absence of outside influences, though the neglection of quantum interactions may result in deviations from reality for measurements on individual atoms and molecules.

(Fv611 (talk) 14:48, 17 May 2017 (BST) TST considers only the reaction coordinate - how could that tell you about the vibrational modes? Also generally rates predicted from TST are not accurate) System B: F-H-H

Question 1: Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved? F + H2 -> H + HF = exothermic H + HF -> H2 + F = endothermic The H-F bond is stronger than the H-H bond. Therefore the formation of the H-F bond is thermodynamically favored (releases energy), and it requires energy to break the H-F bond (endothermic).

(Fv611 (talk) 14:48, 17 May 2017 (BST) You don't justify your statements in any way. You could have referred to the shape of the surface, or referenced bond strenghts.) Question 2: Locate the approximate position of the transition state.

The transition state is approximately located at F-H = 1.808658104 Å, H-H = 0.75 Å. This state core closely resembles H-H than F-H, in accordance with the Hammond Postulate (since H-H is a higher energy state, the transition state more closely resembles it than the low energy F-H).

Question 3: Report the activation energy for both reactions.

H-F + H -> H-H + F: Activation energy = 30.6 kcal/mol H-H + F -> H-F + H: Activation energy = 0.6 kcal/mol The relative energies of each state were determined from the potential energy surface at the points indicated (top left = H-F + H, center = transition state, right = H-H + F).

(Fv611 (talk) 14:48, 17 May 2017 (BST) Your energies are not accurate. This is the problem with point-and-click approaches.) Question 4: In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally? (H-H + F -> H-F + H)

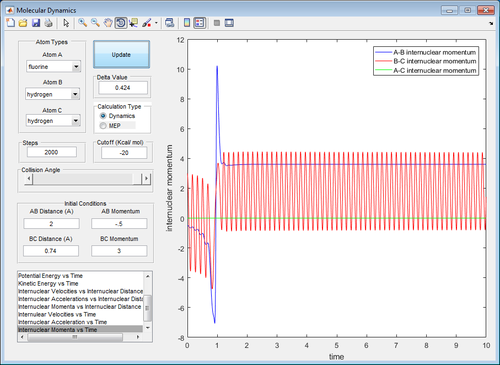
The energy that is released during the breaking of the H-H bond and the formation of H-F goes into the vibration of the H-F bond. This can be seen in the plot below, where the A-B internuclear momentum increases as a result of bond formation. The increased bond vibration could potentially be detected by infrared spectroscopy.

(Fv611 (talk) 14:48, 17 May 2017 (BST) Your plot is too zoomed in and therefpre does not show what you say.)

Question 5: The cases studied are an illustration of Polanyi's empirical rules. Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

Polanyi's rules state that 'vibrational energy is more efficient in promoting a late-barrier reaction (that is, a transition state resembling the products) than translational energy, whereas the reverse is true for an early barrier reaction.' (Zhaojun Zhang, Yong Zhou, Dong H. Zhang, Gábor Czakó and Joel M. Bowman., J. Phys. Chem. Lett., 2012, 3 (23), pp 3416–3419)

In our simulation, the reaction H-H + F -> H-F + H proceeds via an early barrier, and the reverse reaction H-F + H -> H-H + F proceeds via a late barrier reaction.

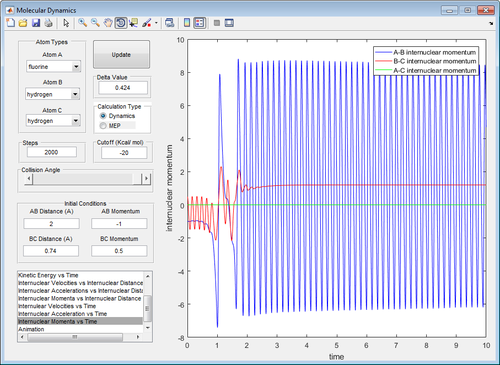
In the early barrier reaction (H-H + F -> H-F + H), we see that a large initial vibrational energy (momentum B-C = 3) and a small translational energy (momentum A-B = -0.5) is not enough to produce H-F (first image). However, increasing the translational energy slightly (momentum A-B = -1) is enough to produce H-F, even with a greatly reduced vibrational energy (momentum B-C = 0.5)(second image).

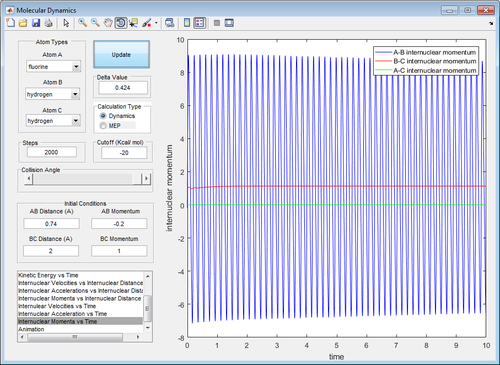
In the late barrier reaction (H-F + H -> H-H + F), we see that a large initial translational energy (momentum B-C = 1) and a small vibrational energy (momentum A-B = -0.2) is not enough to produce H-H (first image). However, increasing the vibrational energy (momentum A-B = -0.8) is enough to produce H-F, even with a reduced translational energy (momentum B-C = 0.1)(second image).

(Fv611 (talk) 14:48, 17 May 2017 (BST) Very good examples. Well done!)