Sn3215
Introduction
This lab focused on optimization+frequency calculations, which were performed using Gaussview. All runs were performed using the method B3LYP and the 6-31G basis set. First, molecules of NH3, N2 and H2 were constructed in Gaussview and optimized with the settings above. Vibrational frequencies and charge distribution of the optimized molecules were analyzed, and the energies of the optimized molecules were also used to calculate the change in enthalpy for the Haber-Bosch Process: N2 + 3H2 -> 2NH3.
In the second and final part of the lab, a molecule of BH3 was optimized and its dipole moment, vibrational frequencies and molecular orbitals were analyzed using Gaussview. Other data such as bond length, bond angle, and point group were also analyzed for all the molecules in the wiki.
NH3 Optimization
Run 1
NH3 |
Method: B3LYP
Basis Set: 6-31G
N-H Bond Length: 1.01798 angstroms
H-N-H Bond Angle: 105.741 degrees
Final energy: -56.55776873 a.u.
RMS Gradient Norm: 0.00000485 a.u.
Point Group: C3V
| Item | Value | Threshold | Converged? |
|---|---|---|---|
| Maximum Force | 0.000004 | 0.000450 | YES |
| RMS Force | 0.000004 | 0.00030 | YES |
| Maximum Displacement | 0.000072 | 0.001800 | YES |
| RMS Displacement | 0.000035 | 0.001200 | YES |
Vibrations
How many modes do you expect from the 3N-6 rule?
A: 6
Which modes are degenerate (ie have the same energy)?
A: Modes 2 and 3 are degenerate, as are modes 5 and 6.
Which modes are "bending" vibrations and which are "bond stretch" vibrations?
A; Modes 1, 2 and 3 are bending vibrations. Modes 4, 5 and 6 are stretching vibrations.
Which mode is highly symmetric?
A: Mode 4 exhibits symmetric bond stretching, and Mode 1 exhibits symmetric bond angle bending.
One mode is known as the "umbrella" mode, which one is this?
A: Mode 1 is the "umbrella" mode.
How many bands would you expect to see in an experimental spectrum of gaseous ammonia?
A: 2, as there are 4 different vibrational energies, but modes 4, 5 and do not change the dipole moment of the molecule significantly and therefore are not vibrationally active.
Charge Analysis

The central nitrogen atom carries a negative charge of -1.125, and each hydrogen carries a positive charge of 0.375. This indicates that charge is localized around the nitrogen atom, due to the relatively greater electronegativity of nitrogen.
H2 Optimization
Run 1
H2 |
Method: B3LYP
Basis Set: 6-31G
H-H Bond Length: 0.74279 angstroms
Final energy: -1.17853936 a.u.
RMS Gradient Norm: 0.00000017 a.u.
Point Group: D*H
| Item | Value | Threshold | Converged? |
|---|---|---|---|
| Maximum Force | 0.000000 | 0.000000 | YES |
| RMS Force | 0.000000 | 0.000300 | YES |
| Maximum Displacement | 0.000000 | 0.001800 | YES |
| RMS Displacement | 0.000001 | 0.001200 | YES |
Vibrations
H2 has one vibrational mode (stretching) at a frequency of 4465.68 Hz.
Charge Analysis
H2 is a homodinuclear molecule and has no dipole moment.
N2 Optimization
Run 1
N2 |
Method: B3LYP
Basis Set: 6-31G
N-N Bond Length: 1.10553 angstroms
Final energy: -109.52412867 a.u.
RMS Gradient Norm: 0.00005962 a.u.
Point Group: D*H
| Item | Value | Threshold | Converged? |
|---|---|---|---|
| Maximum Force | 0.000103 | 0.000450 | YES |
| RMS Force | 0.000103 | 0.000300 | YES |
| Maximum Displacement | 0.000024 | 0.001800 | YES |
| RMS Displacement | 0.000046 | 0.001200 | YES |
Vibrations
N2 has one vibrational mode (stretching) at a frequency of 2457.03 Hz.
Charge Analysis
N2 is a homodinuclear molecule and has no dipole moment.
The Haber-Bosch Process
N2 + 3H2 -> 2NH3
E(NH3) = -56.55776873 a.u.
E(N2) = -109.52412867 a.u.
E(H2) = -1.17853936 a.u.
ΔE = 2*E(NH3)-[E(N2)+3*E(H2)]
= 2*(-56.55776873)-[-109.52412867+3*(-1.17853936)]
= -0.05579071 a.u.
= -146.48kJ/mol
The reaction has a negative change in overall energy, indicating that NH3 is more stable than the the gaseous reactants.
A literature value of -90.4kJ/mol confirms that the reaction is exothermic.[1] The difference between the calculated and literature values may be attributed to a slight inaccuracy in the original energy calculation, which was then magnified when converting from a.u. to kJ.
BH3 Optimization
Run 1
BH3 |
Method: B3LYP
Basis Set: 6-31G
B-H Bond Length: 1.19232 angstroms
H-B-H Bond Angle: 120 degrees
Final energy: -26.61532364 a.u.
RMS Gradient Norm: 0.00000211 a.u.
Point Group: D3H
The calculated bond length compared well to a literature value of 1.19 angstroms.[2]
| Item | Value | Threshold | Converged? |
|---|---|---|---|
| Maximum Force | 0.000004 | 0.000450 | YES |
| RMS Force | 0.000003 | 0.000300 | YES |
| Maximum Displacement | 0.000017 | 0.001800 | YES |
| RMS Displacement | 0.000011 | 0.001200 | YES |
Vibrations
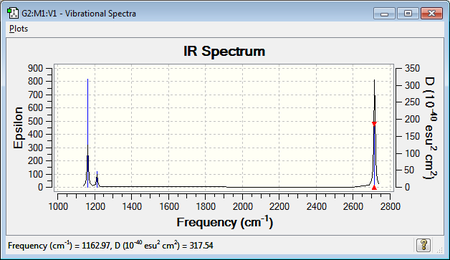
From the 3N-6 rule for non-linear molecules, six vibrational modes are expected for BH3. Of the six modes, modes 2 and 3 are degenerate, as are modes 5 and 6.
Modes 1, 2, and 3 are bending modes, and modes 4, 5, and 6 are stretching modes. As observed in the vibrations of NH3, the stretching modes occur at higher frequencies than the bending modes.
The six vibrational modes produce three peaks in the IR spectrum of BH3, due to the two pairs of degenerate modes, and the vibrationally inactive mode 4 which does not change the dipole moment of the molecule.
Charge Analysis

From the diagram, it is clear that BH3 has a much less significant dipole moment than NH3, due to the small difference in electronegativity between boron and hydrogen. The three hydrogen atoms are slightly more electronegative than boron and draw electron density towards them, resulting in their negative charge and a positive charge on the central boron.
Molecular Orbital Analysis
BH3 is an electron deficient molecule with only six valence electrons, and therefore does not conform to the octet rule.

The 1s orbital of boron is too low in energy to contribute to bonding (~-6.8 a.u), and does not overlap with the hydrogen orbitals. it is denoted as the 1σ orbital.

The 2s orbital of boron can interact in-phase with the three 1s hydrogen orbitals to create a bonding 2σ molecular orbital as seen below. Electron density between all four atoms is strong, and there are no nodal planes.


One lobe of the boron 2px orbital can interact with two in-phase hydrogen 1s orbitals (green interaction in the leftmost picture above), and the other lobe can interact positively with the remaining hydrogen (red interaction in the leftmost picture above). This bonding MO part of a degenerate pair with the orbital in the center (above), which shows the interaction between one lobe of the boron py orbital and an in-phase hydrogen and an identical (but reversed phase) interaction between the other lobe of the py orbital and a hydrogen. The third hydrogen lies on a node of the py orbital, and therefore does not contribute to this MO. These two degenerate orbitals are the highest occupied molecular orbitals (HOMO) of the BH3 molecule.
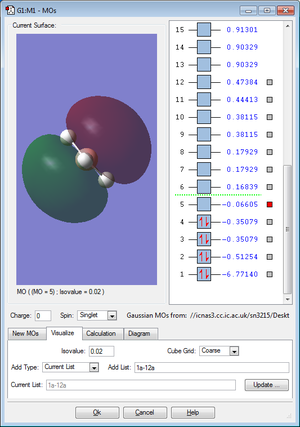
The lowest occupied molecular orbital (LUMO) in borane is the unoccupied 2pz orbital, which contains all three hydrogen atoms in its nodal plane. This orbital does not contribute to bonding.

The out-of-phase interaction between the boron 2s orbital and the three hydrogen 1s orbitals results in an antibonding MO with three nodal planes, each intersecting with one B-H bond. It is denoted as the 1σ* orbital.