Smn216
Ammonia and the Haber-Bosch process
NH3 optimization
- Calculation method: RB3LYP
- Basis: 6-31G(d,p)
- Final energy: -56.55776873 (a.u.)
- RMS gradient: 0.00000485 (a.u.)
- Point group: C3V
- N-H bond distance: 1.01798 Å
- H-N-H bond angle: 105.741°
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
Ammonia |
The optimisation file for NH3 is liked to here
NH3 vibrations
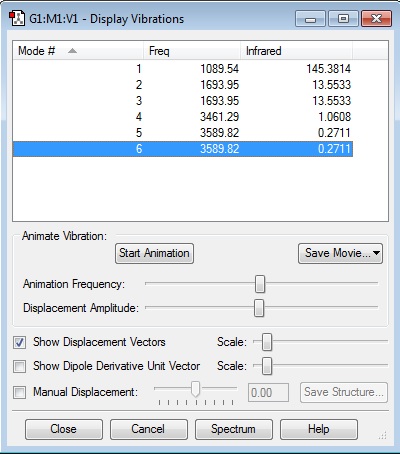
- The 6 vibration modes are expected as NH3 is an asymmetrical (non-linear) molecule with 3 atoms, therefore the 3N-6 rule applies.
- Modes 2 & 3 are degenerate with respect to each other and so are 5 & 6 because each pair has the same frequency (and therefore the same energy).
- Bending modes: 1,2 & 3.
- Stretching modes: 4,5 & 6.
- Mode 4 is highly symmetric and mode 1 is the umbrella mode.
- We expect to see 2 bands in the experimental spectrum of gaseous ammonia because mode 4 is symmetrical so it is IR inactive, but also the intensities of modes 5 and 6 are so low (even smaller than mode 4) that they wouldn't show on the spectrum either. Therefore, one band would be seen due to mode 1 and the second due to modes 2 and 3 (degenerate).
Atomic charge of NH3
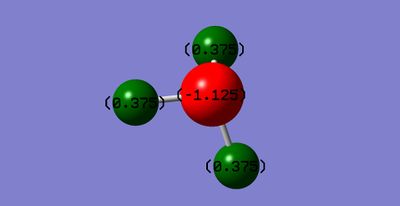
The nitrogen atom has a negative charge and the hydrogen atoms are positively charged. This is due to the difference in electronegativities; the nitrogen atom is more electronegative so it is more able to pull the electrons in the bond to itself and hence create dipoles. The dipoles on the atoms are permanent because the molecule is asymmetrical so the charges do not cancel. The image below shows that the nitrogen atom (red) has a charge of -1.125 and each hydrogen atom (green) has a +0.375 charge:
H2 optimisation
Hydrogen |
- Calculation method: RB3LYP
- Basis: 6-31G(d,p)
- Final energy: -1.17853936 (a.u.)
- RMS gradient: 0.00000017 (a.u.)
- Point group: D∞h
- H-H bond distance: 0.74279 Å
- H-H bond angle: 180°
- Vibration frequency: 4465.68 cm-1 (therefore it is not negative)
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
The optimisation file for H2 is liked to here
N2 optimisation
Nitrogen |
- Calculation method: RB3LYP
- Basis set: 6-31G(d,p)
- Final E: -109.52412868 au
- RMS gradient: 0.00000060 au
- Point group: D∞h
- N-N bond distance: 1.10550 Å
- N-N bond angle: 180°
- Vibration frequency: 2457.33 cm-1 (therefore it is not negative)
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
The optimisation file for N2 is liked to here
The Haber-Bosch process
N2 + 3H2 → 2NH3
- E(NH3)= -56.55776873 (a.u.)
- 2*E(NH3)= -113.1155375 (a.u.)
- E(N2)= -109.52412868 (a.u.)
- E(H2)= -1.17853936 (a.u.)
- 3*E(H2)= -3.53561808 (a.u.)
- ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.0557907 (a.u.) = -146.48 kjmol-1(2d.p.)
Therefore Ammonia is more stable than hydrogen and nitrogen because the reaction is exothermic, so NH3 has lower energy.
Choice of molecule: F2
F2 optimization
- Calculation method: RB3LYP
- Basis: 6-31G(d,p)
- Final energy: -199.49825218 (a.u.)
- RMS gradient: 0.00007365 (a.u.)
- Point group: D∞h
- F-F bond distance: 1.40281 Å
- F-F bond angle: 108°
Item Value Threshold Converged? Maximum Force 0.000128 0.000450 YES RMS Force 0.000128 0.000300 YES Maximum Displacement 0.000156 0.001800 YES RMS Displacement 0.000221 0.001200 YES

Fluorine |
The optimisation file for F2 is liked to here
F2 vibrations
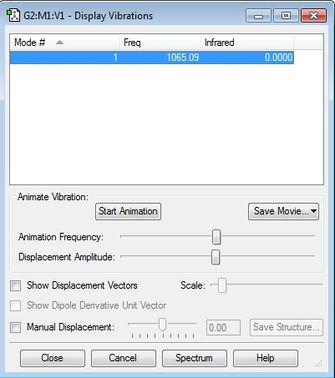
- The single vibration mode is expected as F2 is a linear molecule, therefore the 3N-5 rule applies.
- There is only a stretching mode which is symmetric and therefore the molecule is IR inactive (as shown in the image).
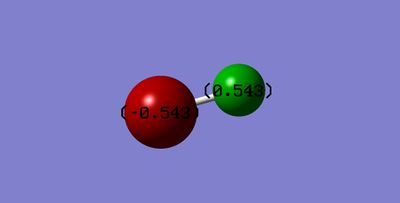
Atomic charge of F2
Fluorine is a diatomic molecule where both the atoms are the same, therefore although fluorine is the most electronegative atom in the periodic table of elements, there is no distortion of the electron cloud as the bond is not polarised. The molecule does not have any dipoles as shown in the image below:

Molecular orbitals of F2
3rd and 4th MOs of fluorine
- These MOs come from the overlap of the 2s orbitals of each fluorine atom. The 3rd MO is the bonding orbital because it is shaded in one colour so it is a single phase, whereas the 4th is the antibonding orbital because the lobes are different colours/phases.
- There is no significant mixing of any of fluorine's MOs because the energy gap between 2s and 2p orbitals is too large.
- The energy of the orbitals are relatively low, but not as deep in energy compared to the two 1s combination of MOs (-1 vs -24 ). Also, both the orbitals are very similar in energy (-1.1 vs -1.3, where -1.1 is the energy of the antibonding orbital/4th).
- Both MOs are filled but neither are the HOMO of F2. This is because if both the orbitals are occupied the electrons cancel out meaning that no overall bond is formed; it has no effect on bonding.


5th MO of fluorine
- The 5th MO is the overlap of a 2p-orbital from each fluorine atom.
- It is a bonding MO because the middle part (in green in the image below) shows that the lobes of each orbital which overlap are of the same phase.
- The MO is filled but its not the HOMO and its energy is greater than the 3rd and 4th MOs (-0.59).
- This MO results in the bond between the two atoms because its antibonding MO is empty. It is the end on overlap so the bond is sigma.

6th and 7th MOs of fluorine
- The remaining two 2p orbitals also overlap to form two bonding MOs and two antibonding MOs. The two bonding MOs are the 6th and 7th MOs.
- These two MOs are degenerate because each orbital is perpendicular to the bond (-0.52).
- Both orbitals are occupied (but not the HOMO).
- The image below shows the shape of the MOs, each of the two MOs has a different orientation with respect to the bond:

8th and 9th MOs of fluorine
- The two antibonding orbitals resulting from the overlap of the two remaining p orbitals are MOs 8 and 9.
- These two orbitals are also degenerate and they have a slightly higher energy than the bonding orbitals (-0.39).
- Both antibonding orbitals are filled which cancels out the electrons in the bonding orbitals, so it has no effect on the bonding in the molecule.
- The MOs are occupied and as they are degenerate, they are both the HOMO of fluorine; there is only one MO remaining which is unoccupied, therefore these must be the HOMOs.
- The image below shows their shape (not their correct orientations):

H-F (independence)
H-F optimisation
- Calculation method: RB3LYP
- Basis: 6-31G(d,p)
- Final energy: -100.42746153 (a.u.)
- RMS gradient: 0.00001092 (a.u.)
- Point group: C∞v
- H-F bond distance: 0.92540 Å
- H-F bond angle: 180°
Item Value Threshold Converged? Maximum Force 0.000019 0.000450 YES RMS Force 0.000019 0.000300 YES Maximum Displacement 0.000016 0.001800 YES RMS Displacement 0.000022 0.001200 YES

Hydrogen fluoride |
The optimisation file for H-F is liked to here
H-F vibrations
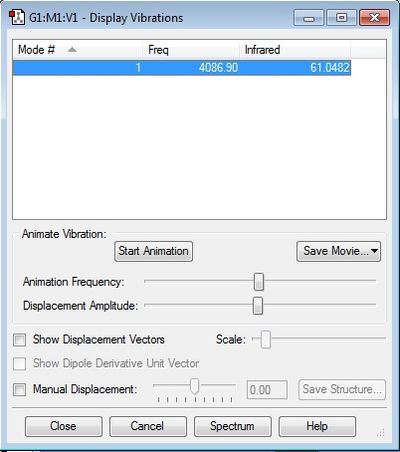
- The single vibration mode is expected as HF is a linear molecule, therefore the 3N-5 rule applies.
- There is only a stretching mode which is asymmetric and therefore the molecule is IR active. The image shows that the infrared intensity is 61, so unlike diatomic molecules which are symmetrical, HF can absorb IR radiation.
Atomic charge of H-F
- Hydrogen fluoride has dipoles because the fluorine atom is very electronegative, and there is a big difference between the electronegativities of hydrogen and fluorine, so the fluorine is more able to pull the electrons in the bond closer to itself, distorting the electron cloud.
- Therefore the fluorine atom (red) is negatively charged and the hydrogen atom (green) has a positive charge.
- ALSO, the bond is so polarised that it has great ionic character and contribution, making it stronger and shorter than expected.