SS6416
BH3
Computational Level and Basis Set: B3LYP/6-31G(d,p)
Summary Table
Item Table
Item Value Threshold Converged? Maximum Force 0.000161 0.000450 YES RMS Force 0.000105 0.000300 YES Maximum Displacement 0.000638 0.001800 YES RMS Displacement 0.000418 0.001200 YES
Frequency analysis log file: Media:sas_bh3_freq.log
Low Frequencies lines
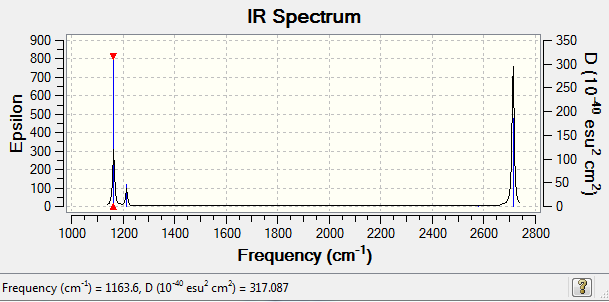
Low frequencies --- -0.2456 -0.1129 -0.0054 44.0270 45.1846 45.1853 Low frequencies --- 1163.6049 1213.5924 1213.5951
Optimised BHOptimised Borane molecule |
Vibrational spectrum for BH3
| wavenumber (cm-1) | Intensity (arbitrary units) | symmetry | IR active? | type |
| 1163 | 92 | A2 | yes | out-of-plane bend |
| 1213 | 14 | E' | slight | in-plane bend |
| 1213 | 14 | E' | slight | in-plane bend |
| 2580 | 0 | A1' | no | symmetric stretch |
| 2713 | 126 | E' | yes | asymmetric stretch |
| 2713 | 126 | E' | yes | asymmetric stretch |
There are only 3 peaks observed in the IR spectrum, as the first frequency 1163 cm-1 has a strong intensity. Both the second and third frequencies of 1213 cm-1 are degenerate and have a low intensity, so they are observed as one small peak. The fourth frequency 2580 cm-1 has no net dipole moment, so has no intensity, so is not observed. The final two frequencies at 2713 cm-1 are degenerate and have a strong intensity, so are observed as one strong signal.
Smf115 (talk) 16:33, 28 May 2018 (BST)Correct assignment of the modes and symmetries and clearly explained answer!
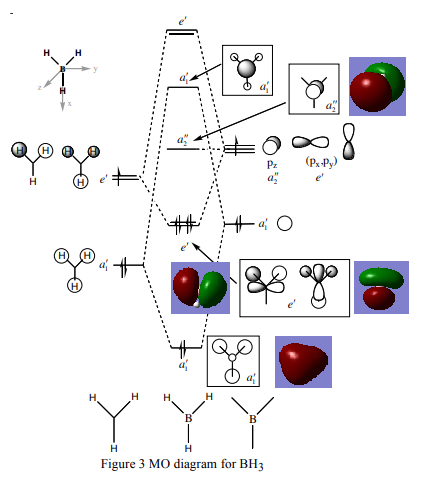
Molecular Orbitals for BH3
The Molecular Orbital diagram for BH3 is shown below[1]:
There are no real significant differences between the 'real' and LCAO molecular orbitals. Thus, qualitative MO theory is a very accurate representation of the real MOs. This is a useful way of visualising the real MOs.
Smf115 (talk) 16:38, 28 May 2018 (BST)Good highlight of the useful nature of the qualitative MOs. To improve it would be nice to see all of the MOs (2-8) on the diagram and for the differences visible in some of the AO contributions between the calculated and qualitative MOs (such as in 3a1') to be highlighted.
NH3
Computational Level and Basis Set: B3LYP/6-31G(d,p)
Summary Table
Item Table
Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000014 0.001800 YES RMS Displacement 0.000009 0.001200 YES
Frequency analysis log file: Media:ss6416_nh3_opt.log
Low Frequencies lines
Low frequencies --- -0.0128 -0.0014 0.0015 7.1034 8.1048 8.1051 Low frequencies --- 1089.3834 1693.9368 1693.9368
Optimised NHOptimised Ammonia molecule |
NH3BH3
Computational Level and Basis Set: B3LYP/6-31G(d,p)
Summary Table
Item Table
Item Value Threshold Converged? Maximum Force 0.000123 0.000450 YES RMS Force 0.000058 0.000300 YES Maximum Displacement 0.000585 0.001800 YES RMS Displacement 0.000320 0.001200 YES
Frequency analysis log file: Media:ss6416_nh3bh3_freq.log
Low Frequencies lines
Low frequencies --- -0.0005 0.0006 0.0007 16.8436 17.4462 37.3291 Low frequencies --- 265.8243 632.2043 639.3227
Optimised NHBHOptimised Ammonia-Borane molecule |
Association Energy of NH3BH3
E(NH3BH3)= -83.22469 Eh
E(NH3)= -56.55777 Eh
E(BH3)= -26.61532 Eh
Association Energy = -0.0516 Eh = -135 kJ/mol
The B-N bond strength of 135.5 kJ/mol is weak as covalent bonds strengths are typically in the range 150-400 kJ/mol[2]. Furthermore, if compared to an isoelectronic molecule in ethane, the bond energy for C-C in ethane is 377 kJ/mol[3]. Therefore we can conclude that it is a weak bond, especially as we would expect some ionic character in the bond due to the electronegativity difference between Boron and Nitrogen. This is due to the fact that it is a dative covalent bond.
BBr3
Computational Level and Basis Set: B3LYP/6-31G(d,p)LANL2DZ
Summary Table
Item Table
Item Value Threshold Converged? Maximum Force 0.000008 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000036 0.001800 YES RMS Displacement 0.000018 0.001200 YES
Frequency analysis log file: Media:ss6416_bbr3_freq.log
Low Frequencies lines
Low frequencies --- -0.0137 -0.0064 -0.0046 2.4315 2.4315 4.8421 Low frequencies --- 155.9631 155.9651 267.7052
Optimised BHOptimised BBr3 molecule |
Investigating Aromaticity
Benzene
Computational Level and Basis Set: B3LYP/6-31G(d,p)
Summary Table
Item Table
Item Value Threshold Converged? Maximum Force 0.000193 0.000450 YES RMS Force 0.000079 0.000300 YES Maximum Displacement 0.000790 0.001800 YES RMS Displacement 0.000277 0.001200 YES
Frequency analysis log file: Media:ss6416_c6h6_opt.log
Low Frequencies lines
Low frequencies --- -17.2058 -14.9379 -14.9379 -0.0055 -0.0055 -0.0006 Low frequencies --- 414.1053 414.1053 620.9429
Optimised BHOptimised Benzene molecule |
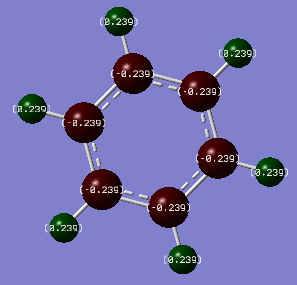
Charge Distribution:
Borazine
Computational Level and Basis Set: B3LYP/6-31G(d,p)
Summary Table
Item Table
Item Value Threshold Converged? Maximum Force 0.000085 0.000450 YES RMS Force 0.000033 0.000300 YES Maximum Displacement 0.000308 0.001800 YES RMS Displacement 0.000079 0.001200 YES
Frequency analysis log file: Media:ss6416_borazine_freq.log
Low Frequencies lines
Low frequencies --- -2.7054 -0.0497 -0.0037 0.0202 1.9426 1.9473 Low frequencies --- 289.7142 289.7150 404.4326
Optimised BHOptimised Borazine molecule |
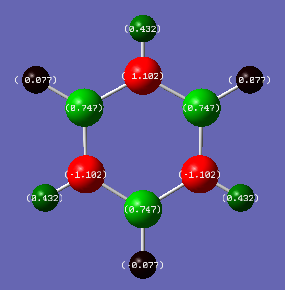
Charge Distribution:
Charge Distribution Comparison
-
Benzene Charge Distribution -
Borazine Charge Distribution
| Atom | Charge |
|---|---|
| C | -0.239 |
| H | 0.239 |
| Atom | Charge |
|---|---|
| N | -1.102 |
| B | 0.747 |
| HN | 0.432 |
| HB | -0.077 |
There is a much smaller difference in charge distribution for benzene than there is for borazine. This is due to the very small electronegativity difference of 0.4 on the Pauling Scale between carbon and hydrogen in benzene. This results in bonds which are not very polar and an even distribution of charge across the molecule. As Carbon is more electronegative than hydrogen, the negative charge -0.239 resides on the Carbon and the positive charge +0.239 resides on the Hydrogen.
Borazine has a much larger charge distribution, due to the large electronegativity of Nitrogen of 3.0 on the Pauling Scale. Boron and Hydrogen have electronegativities of 2.0 and 2.2 respectively. Thus the large electronegativity difference between Nitrogen and Boron/Hydrogen, results in very polar sigma bonds. As the nitrogen is more electronegative, more electron density resides around it, so the Nitrogen atom is strongly negatively charged with -1.102 and the boron is strongly positively charged with +0.747 due to the lack of electron density around it. Due to this the hydrogen atoms are bonded to Nitrogen differently than they are to Boron. The hydrogens bonded to the nitrogen having protic nature, thus they are slightly positively charged with +0.432. The large magnitude is due to the highly polar N-H bond. The hydrogens bonded to the boron have hydridic nature, so they are slightly negatively charged at -0.077. The small magnitude is due to the low polarity of the B-H bond.
Benzene has a D6h point group and Borazine has a D3h point group. It is easy to observe that benzene is not a polar molecule as the dipole of each C-H bond has an opposing dipole on the opposite side of the ring. It is more difficult to observe whether Borazine is a polar molecule as there is not an identical bond opposite on the ring to oppose each dipole. However each N-H or B-H dipole is cancelled out by the sum of the other two N-H or B-H dipoles respectively at 120° to the original N-H or B-H bond. Therefore Borazine is not a polar molecule either.
Smf115 (talk) 13:54, 1 June 2018 (BST)Very good charge analysis covering a range of factors to explain the distributions and good detail including the point groups of the molecules.
Molecular Orbitals
| Benzene | Borazine | Comparison |
|---|---|---|
|
|
MO17 of both benzene and borazine show the pi bonding molecular orbital of each molecule. The orthogonal pz orbitals in both benzene and borazine are in phase and so overlap constructively forming the fully bonding pi molecular orbitals in each case. For borazine the MO is not fully symmetric due to the electronegativity difference between Nitrogen and Boron, so more electron density resides near the Nitrogen. |
|
|
MO14 for benzene and MO15 for borazine. Both are sigma bonding orbitals using either the px or px orbitals in the plane of the the molecule which interfere constructively between the C-H bonds, resulting in the bonding lobes. The nodal planes along the C-H bonds are due to the change of phase of the p orbitals used in the bonding. Both MOs are fully occupied with C3 axis perpendicular to the molecules through the middle of them. In benzene the Mo is fully symmetric, whereas in borazine the MO is slightly less symmetric, with slightly more electron density residing around the Nitrogen than the Boron due to the electronegativity difference. |
|
|
MO20 of both benzene and borazine is a pi bonding orbital but is higher in energy than MO17, due to the nodal plane through the molecule. Three orthogonal pz orbitals on each side of the ring overlap constructively in both molecules. the nodal plane through the plane of the molecule is due to the change in phase of the pz orbitals. Due to the out of phase overlap between nodal planes, there is some antibonding character as the pz orbitals interfere destructively. |
Aromaticity
A theory for aromaticity was proposed by Kekule, in that benzene consisted of alternating single and double bonds. However it was found that every C-C bond in benzene had the same length using X-ray and neutron diffraction and so this showed that a different structure, as the double and single bonds proposed by Kekule would have had different lengths. Huckel came up with a different set of rules[4], which a molecule must obey to be aromatic: 1. The molecule must contain (4n+2) p electrons orthogonal to the ring system. 2. The molecule must be planar. 3. The molecule must have a cyclic, contiguous array of p orbitals perpendicular to the the plane of the ring. The aromatic stabilisation is generated by overlapping pz orbitals, creating the delocalisation of pi electrons in the ring. This gives the bonds an intermediate strength in between that of a single or double bond. Borazine has a very similar structure to benzene and is isoelectronic with benzene. The similar properties of borazine show that it is aromatic too.
The occupied molecular orbitals generated from the optimisation of benzene on Gaussian reflect the predicted MOs from the LCAO method very well qualitatively. However for borazine, the real molecular orbitals are more difficult to predict due to the electronegativity difference between nitrogen and boron, means that the spread of electron density will not be fully symmetric, as it is difficult to predict what effect the difference in electronegativity will have on the shape of the MOs relative to benzene. Therefore qualitatively predicting this in the LCAO method is more difficult than that in benzene due to its symmetric structure. Furthermore, as there is some ionic character in the borazine bonds, the shape of the MOs in borazine is less predictable than for benzene. Many of the fully occupied MOs in both benzene and borazine have cyclic ring-shaped sigma bonding interactions, demonstrating the aromaticity of both structures, as the electrons are most likely to be within the rings of constructive overlap. This therefore shows the delocalisation of the electrons around the ring. This promotes the idea of sigma aromaticity, where the strongly overlapping sigma orbitals contribute to the aromaticity, as displayed in the real MOs, optimised by Gaussian. The concept of sigma aromaticity is displayed strongly in saturated inorganic rings[5].
This model and these rules work well for benzene but begin the break down as benzene adopts a chair conformation at 20°C[6] in the crystalline state due to strong intermolecular forces in the lattice structure. therefore the planarity of the original structure is destroyed, therefore violating Huckel's rules. However, the molecule is still aromatic. Other examples of non-planar aromatic structures include metallobenzenes, 3D boranes and fullerenes[7]. Therefore the overlap of pz orbitals is not a good method to describe aromaticity, despite the fact that non-planar molecules have weaker pz orbital overlap resulting in less delocalisation.
Smf115 (talk) 13:59, 1 June 2018 (BST)Good layout of the key concepts of aromaticity, referenced examples and mention of more complex concepts such as sigma aromaticity. To improve, the LCAO and MO comparison isn't particularly relevant and the MOs could have been used more to illustrate the concept of the overlapping PZ AOS as a bad descriptor.
Smf115 (talk) 14:00, 1 June 2018 (BST)Overall, a good and well presented report.
- ↑ Molecular Orbitals in Inorganic Chemistry, Lecture 4 Tutorial Problem Model Answers, Dr. Patricia Hunt, p.2
- ↑ Chemistry, Ch.7, 7.5 Strength of Ionic and Covalent Bonds
- ↑ Active Thermochemical Tables: Sequential Bond Dissociation Enthalpies of Methane, Ethane, and Methanol and the Related Thermochemistry, B. Ruscic, Journal of Physical Chemistry A, 2015, p.7810-7837
- ↑ Aromatic Chemistry, Lecture 1, Prof. Alan Spivey, May 2017
- ↑ Sigma-aromaticity and sigma-antiaromaticity in saturated inorganic rings, Z. H. Li, J Phys Chem A. 2005 Apr 28;109(16):3711-6
- ↑ Application of AIM Parameters at Ring Critical Points for Estimation of p-Electron Delocalization in Six-Membered Aromatic and Quasi-Aromatic Rings, M. Palusiak & T. M. Krygowski, Chem. Eur. J, 2007, 13, 7996-8006
- ↑ Main Group Chemistry, Lecture 5, Dr. Laura Patel, February 2018