This tutorial shows how to set up and run a Hairy Probes (HP) ^[1] DFT calculation using the CP2K2022.1 computational package. Our implementation of Hairy Probes within the CP2K code is presented in ref. ^[2]. The module required to run a HP-DFT calculation is still not part of the official release of CP2K; this tutorial shows how to download and compile CP2K2022.1 with the necessary HP-DFT module.

Compiling CP2K2022.1 with Hairy Probes

1. Download CP2K2022.1 and set up the required libraries:

  git clone -b support/v2022.1 https://github.com/cp2k/cp2k.git ~/${INSTALL_DIR}/cp2k

2. Download the Hairy Probes modules:

  git clone https://gitlab.doc.ic.ac.uk/rgc/hairy_probes_dft_cp2k.git ~/${INSTALL_DIR}/Hairy_probes_modules

3. Copy the Hairy Probes modules (all the modules contained in the Hairy_probes_modules repository) in the source code folder of CP2K:

  cp ~/${INSTALL_DIR}/Hairy_probes_modules/* ~/${INSTALL_DIR}/cp2k/src

4. Continue compiling CP2K2022.1 per usual. For example:

  cd ~/${INSTALL_DIR}/cp2k/tools/toolchain/
  ./install_cp2k_toolchain.sh --no-check-certificate --with-elpa=no 
  source ~/${INSTALL_DIR}/cp2k/tools/toolchain/install/setup
  cp ~/${INSTALL_DIR}/cp2k/tools/toolchain/install/arch/* ~/cp2k/arch/
  cd ~/${INSTALL_DIR}/cp2k 
  make -j 24 ARCH=local VERSION="ssmp sdbg psmp pdbg" &> make.log

(This example shows how to compile CP2K2022.1 using the provided install_cp2k_toolchain.sh script, which builds the necessary libraries and architecture files. Any other strategy to compile the code, e.g. easybuild, is equally valid. The important point is to add the necessary modules to the source code before compiling).

Run an HP-DFT calculation

To run an HP-DFT calculation the following section needs to be added under the DFT section of the input:

    &HAIR_PROBES 
      T 300
      MU 0.500000
      ATOM_IDS 1..54 
      EPS_HP 1.0E-5
    &END HAIR_PROBES
    &HAIR_PROBES 
      T 300
      MU -0.500000     
      ATOM_IDS 347..1045
      EPS_HP 1.0E-5
    &END HAIR_PROBES
    &HAIR_PROBES 
      ALPHA 0.01
      T 300
      MU 0.000000     
      ATOM_IDS 193..543
      EPS_HP 1.0E-5
    &END HAIR_PROBES

The keywords are defined as follows:

T: electronic temperature of the electrons in the reservoirs;
MU: electrochemical potential of the electrons in the reservoirs;
ATOM_IDS: indices of the atoms in the system coupled with hairy probes;
ALPHA: parameter. A value of ALPHA lower than 1.00 defines a set of probes as 'solution probes';
EPS_HP: defines the accuracy of the HP calculation.

You can repeat the section HAIR_PROBES for as many sets of probes as you want in your calculation. Generally, you want to set ALPHA to be very low for atoms in solution. You can use HAIR_PROBES both for GEO_OPT (geometry optimization) and MD (molecular dynamics) type calculations (as long as the force evaluation (FORCE_EVAL) is done using DFT, of course).

Other important things to know:

To run HP-DFT you need to remove the SMEARING section;
As of now, the HP-DFT implementation only works with STANDARD DIAGONALIZATION (it does not work with OT, for example).

Example Calculation: Parallel-Plate Capacitor

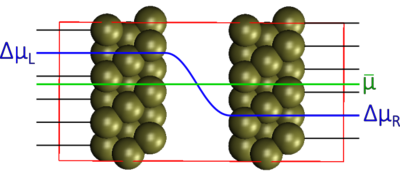
This example shows an HP-DFT calculation performed for a straightforward parallel-plate capacitor model. The model consists of two 3-layer Pt(111)(6x6) slabs separated by 10Å of vacuum. The slabs were built using a conventional unit cell with a lattice parameter of 3.97 Å. The supercell is periodic in x and y (directions parallel to the slabs' surfaces) but not in z (directions perpendicular to the slabs' surfaces), where an implicit Poisson solver was used ^[3] . The calculation was performed at the Γ-point. The PBE functional ^[4] in combination with Grimme's D3 correction ^[5] for dispersion interactions were employed. The valence electrons of the Pt atoms were described using the TZVP-MOLOPT basis set ^[6], while the core electrons were described with a GTH pseudopotential ^[7].

HP-DFT calculation setup

For this calculation, two sets of main probes were coupled with the outermost layer of the capacitor model (atoms 1 to 36 in the left slab and atoms 181 to 216 in the right slab). Electrochemical potentials Δμ_L = 0.5 eV and Δμ_R = -0.5 eV were imposed on the left slab and the right slab respectively. This gave an overall electrochemical potential difference Δμ = |Δμ_L - Δμ_R| = 1 eV across the two plates. The electronic temperature was set at 300K. Since there is no electrolyte in this system, solution probes were not required. The section controlling the HP calculation in the CP2K input therefore is:

    &HAIR_PROBES 
      T 300
      MU 0.500000
      ATOM_IDS 1..36
      EPS_HP 1.0E-5
    &END HAIR_PROBES
    &HAIR_PROBES 
      T 300
      MU -0.500000     
      ATOM_IDS 181..216
      EPS_HP 1.0E-5
    &END HAIR_PROBES

The same calculation was repeated using Δμ_L = 2 eV and Δμ_R = -2 eV to give Δμ = |Δμ_L - Δμ_R| = 4 eV

Results

In this section, a summary of the relevant results is reported. For more details check the full publication

References

↑ M. G. Zauchner, A. P. Horsfield, and T. N. Todorov, Efficient electron open boundaries for simulating electrochemical cells, Physical Review B 97, 0.1103/PhysRevB.97.045116 (2018)
↑ M. Buraschi, A. P. Horsfield and C.S. Cucinotta, Revealing Interface Polarization Effects on the Electrical Double Layer with Efficient Open Boundary Simulations under Potential Control, J. Phys. Chem. Lett. 2024, 15, 4872−4879
↑ M. H. Bani-Hashemian, S. Bruck, M. Luisier, and J. VandeVondele, A generalized poisson solver for firstprinciples device simulations, J Chem Phys 144, 044113 (2016).
↑ J. P. Perdew, K. Burke, and M. Ernzerhof, Generalized gradient approximation made simple, Phys Rev Lett 77, 3865 (1996).
↑ S. Grimme, J. Antony, S. Ehrlich, and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (dft-d) for the 94 elements h-pu, J Chem Phys 132, 154104 (2010).
↑ J. VandeVondele and J. Hutter, Gaussian basis sets for accurate calculations on molecular systems in gas and condensed phases, J Chem Phys 127, 114105 (2007).
↑ S. Goedecker, M. Teter, and J. Hutter, Separable dualspace gaussian pseudopotentials, Phys Rev B Condens Matter 54, 1703 (1996).

[1] M. G. Zauchner, A. P. Horsfield, and T. N. Todorov, Efficient electron open boundaries for simulating electrochemical cells, Physical Review B 97, 0.1103/PhysRevB.97.045116 (2018)

[2] M. Buraschi, A. P. Horsfield and C.S. Cucinotta, Revealing Interface Polarization Effects on the Electrical Double Layer with Efficient Open Boundary Simulations under Potential Control, J. Phys. Chem. Lett. 2024, 15, 4872−4879

[3] M. H. Bani-Hashemian, S. Bruck, M. Luisier, and J. VandeVondele, A generalized poisson solver for firstprinciples device simulations, J Chem Phys 144, 044113 (2016).

[4] J. P. Perdew, K. Burke, and M. Ernzerhof, Generalized gradient approximation made simple, Phys Rev Lett 77, 3865 (1996).

[5] S. Grimme, J. Antony, S. Ehrlich, and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (dft-d) for the 94 elements h-pu, J Chem Phys 132, 154104 (2010).

[6] J. VandeVondele and J. Hutter, Gaussian basis sets for accurate calculations on molecular systems in gas and condensed phases, J Chem Phys 127, 114105 (2007).

[7] S. Goedecker, M. Teter, and J. Hutter, Separable dualspace gaussian pseudopotentials, Phys Rev B Condens Matter 54, 1703 (1996).

[1]

[2]

[3]

[4]

[5]

[6]

[7]