What value do the different components of the gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface?

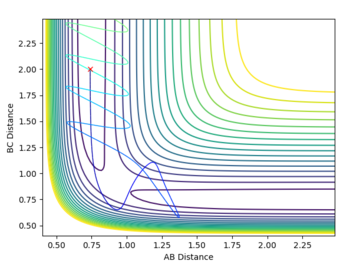
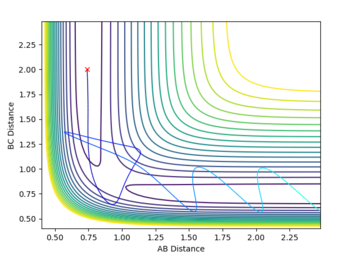
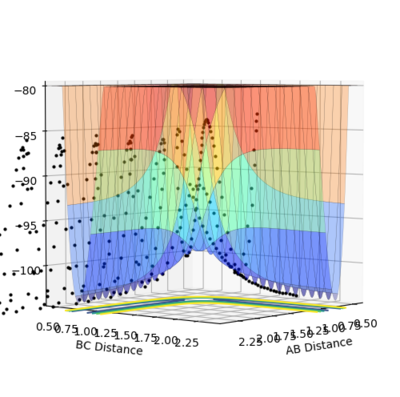
The transition state is present as a saddle point along the product and reactant channel. The reactant channel has a potential energy minima where ∂V(r1)/∂r1=0, and the product channel has a minima where ∂V(r2)/∂r2=0. The transition state is a maximum along these channels, however the transition state is a minimum orthogonal to these channels (saddle point). Here ∂V²(ri)/∂(ri)²<0 at the saddle point and ∂V²(ri)/∂(ri)²= 0 at the reaction channels.

Mm10114 (talk) 20:31, 31 May 2018 (BST) Well explained.

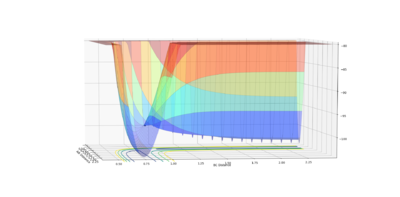
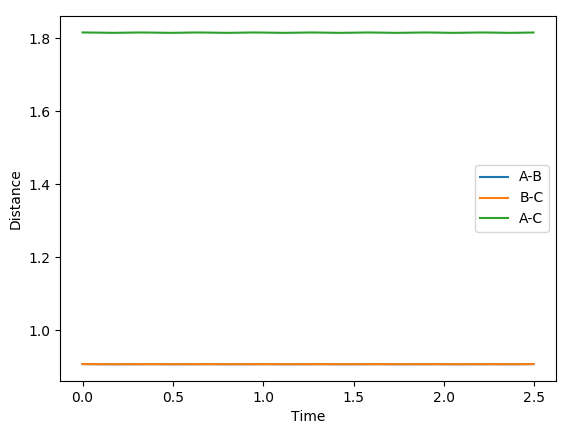
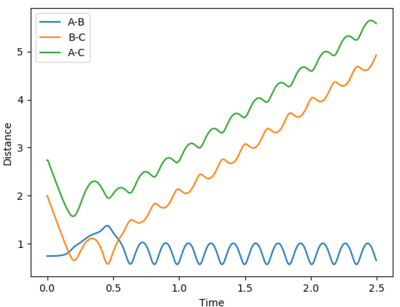
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.

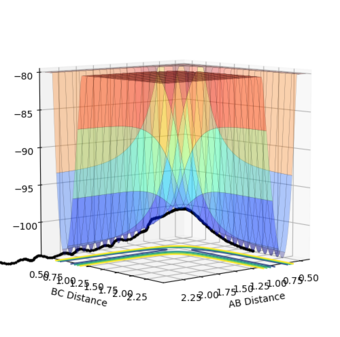
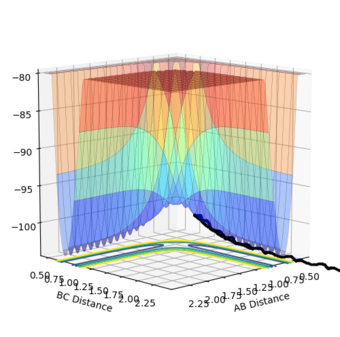
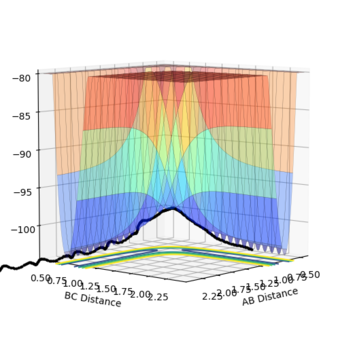
The transition point position is found when the A-C distance and B-C distance both 0.908Å. The potential energy surface point is evidence of this as it shows the bond to be single point at the saddle point. Furthermore, the Internuclear Distances vs Time shows the A-C and A-B plots to overlap, be constant throughout, indicating no oscillation to be present. Mm10114 (talk) 20:31, 31 May 2018 (BST) Could've described briefly how did you find it.

Surface Plot	Surface plot (side view)	Internuclear Distances vs Time

Comment on how the mep and the trajectory you just calculated differ.

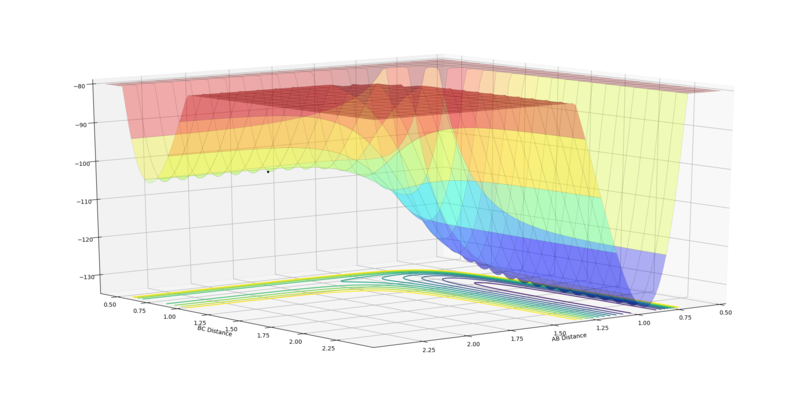
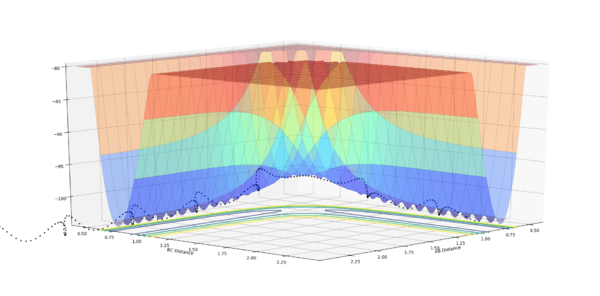
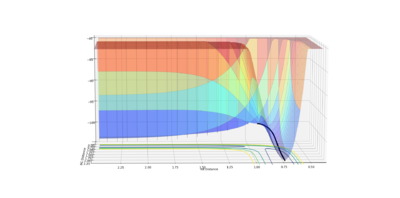
The MEP is the minimum energy path that corresponds to infinitely slow motion, where the velocity always reset to zero in each time step. The momenta is set to zero, hence no oscillation is present, this therefore displays a plot in which the trajectory is straight follows the valley floor to H₁+ H₂-H_3.

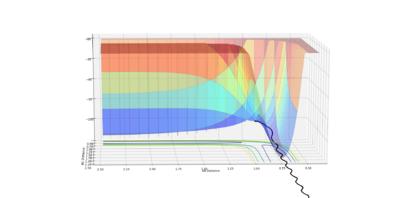
The calculation type was reset to Dynamics, to show the effect mass has upon the trajectory. The plot obtained shows inertia to sway the motion of the atoms, hence leading to a more curved trajectory pattern.

MEP Surface Plot (20,000 steps used)	Dynamics Surface Plot

Complete the table by adding a column with the total energy, and another column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a plot of the trajectory and a small description for what happens along the trajectory.

Experiment Number	p₁	p₂	Total energy	Reactive/Unreactive trajectory	Descriptoin
1	-1.25	-2.5	-99.018	Reactive	The trajectory shown reaches, then exceeds the transition state's saddle point, leading to the formation of products, indicated by the AB product channel.
2	-1.5	-2.0	-100.456	Unreactive	The trajectory does not reach the saddle point, hence the transition state is not reached, and BC product is not formed.
3	-1.5	-2.5	-98.956	Reactive	Here the trajectory surpasses the transition state, leading to the formation of the AB product. The energy is lower than that of experiment 1.
4	-2.5	-5.0	-84.956	Unreactive	The trajectory shows a disordered pathway throughout as the system does not utilise the entire minimum energy reaction pathway. The transition state is reached, however the reaction does not fully proceed to the product pathway. Suggesting the trajectory is unreactive. Atom B oscillates between atoms A and C before reforming the initial AB reactant.
5	-2.5	-5.2	-83.416	Reactive	The trajectory shown here is similar to that of experiment 4. However this lower energy pathway proceeds down the product channel, as indicating a successful reactive pathway. Atom B oscillates between atoms A and C before reforming the initial BC reactant. The internuclear Vs time plot for experiment 5 is similar to that of experiment 4.

State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

The two most basic assumptions of transition state theory ¹:

1)Separation of electronic and nuclear motions, which is known as the Born-Oppenheimer approxiamtion in quantum mechanics

2)Reactant molecules are distributed among their states in accordance with the Maxwell-Boltzmann distribution

This theory makes three further assumptions:

3) Molecular systems that cross the transition state (forming products), cannot reform reactants

4) In the transition state, motion along the reaction coordinate can be treated as only transnational

5) When no equilibrium is present between products and reactants, transition states that are becoming products are distrusted among their states (follows the Maxwell-Boltzmann laws) Not necessary, follows from first assumption

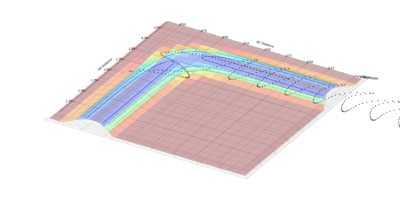
Experiement 4 birds-eye view	Experiement 4 Internuclear Distance Vs Time	Experiment 5	Experiment 5,Surface plot birds-eye view

The results obtained from experiments 4 and 5, does not follow assumption 3 of the transition state theory. Both experiments show the trajectory crossing the transition state, then returning to reactant energy channel. These simulations were run with higher momentum values than needed in order to react, thus leading to high energy trajectory's which do not act as expected.

Mm10114 (talk) 20:31, 31 May 2018 (BST) Well done. However, you've forgot to comment how, in light to these assumptions, the TST predicted reaction rates compare to experimental values.

EXERCISE 2: F - H - H system

Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

The mean bond enthalpy for the H-H is 436 KJmol-1, whilst the H-F enthalpy is 565 KJmol-1. This therefore shows the F + H2 reaction to be exothermic as an excess of 129 KJmol-1 of energy is given out to the surroundings due to the formation of the stronger H-F bond. This therefore can be used to predict that the H + HF reaction will be endothermic as energy is needed to break the strong H-F bond and form the weak H-H bond ².

Mm10114 (talk) 20:31, 31 May 2018 (BST) The 'kilo' in kJ should be lower case, there should be a space between kJ and mol and the ^-1 as upper-script. Keep more attention to the formatting.

Locate the position of the transition state

System	r1 (Å)	r2 (Å)	Transition state (kcal/mol)
F-H-H	1.8106	0.745	-103.752

Transition State

Report the activation energy for both reactions

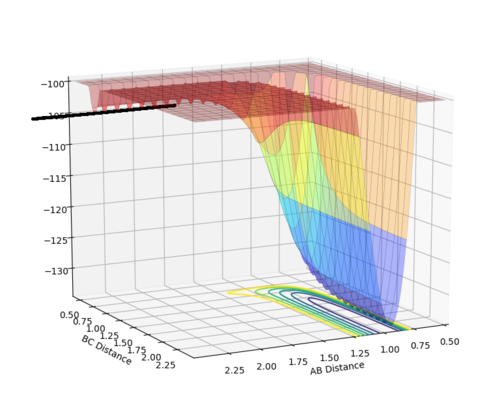
Calculation type was set to MEP, with 200,000 steps.

F + H₂ System, the activation energy was found to be E_A= 30.2533 kcal/mol. Where the r₁ = 1.8306 and r₂ = 0.745

Surface plot of the activation energy	Energy vs Time (potential energy)

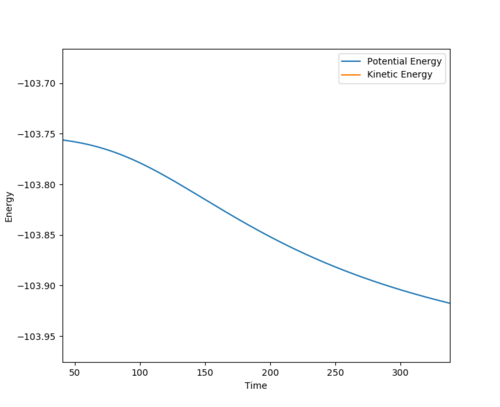
H + F-H System, the activation energy was found to be E_A= 0.246777. Where r₁ - 1.8206 and r₂=0.750

Surface plot of activation energy	Energy vs Time (potential energy)

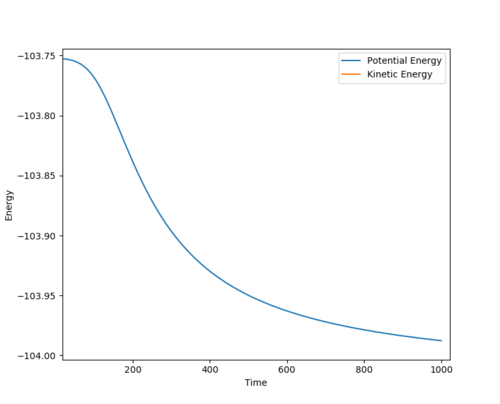
In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?

Identify a set of initial conditions that results in a reactive trajectory for the F + H2, and look at the “Animation” and “Internuclear Momenta vs Time”.

System	r1 (Å)	r2 (Å)	p1	p2	Total energy (kcal/mol)
F + H2	2.5	0.745	-0.8	0	-103.752

These conditions result in a reactive trajectory, allowing the formation of H-F product.

The first law of thermodynamic states "That the total energy of an isolated system is constant", This means that energy cannot be created or destroyed, but can be transformed from one form to another. The internuclear momenta vs time graph shows the momentum of A to be constant until B-C is in a reasonable range to react. This shows a large amount of potential energy being converted into vibration energy. This vibrational energy causes the bond to oscillate at a high rate. Furthermore this large transfer of energy from potential to vibrational can be confirmed experimentally by measuring the change in electromagnetic radiation emitted in the IR region as the reaction proceeds.

Internuclear Momenta vs Time graph

Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

The most important factor in determining the distribution of products is the location of the early barrier (in the reactants channel) and late barrier (in the products channel) on the reaction coordinate¹.

Polanyi's empirical rules show that translational energy most effective to cross early barrier (early transition state, resembles reactants), whereas if the reactants vibrational energy is too high, the reaction may not proceed. This is the opposite for late energy barrier (late transition state, resembles product), where vibrational energy is preferred over translational energy.

F + H₂ System (Earlier barrier)

Situation	rFH (Å)	rHH (Å)	pFH	pHH	Reactive/unreactive
High translational energy	2.4	0.7453	-0.7	-0.2	Reactive
High vibrational energy	2.4	0.7453	-0.7	-2	Unreactive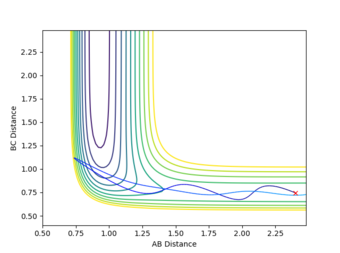

H + H-F System (Late barrier)

Situation	rFH (Å)	rHH (Å)	pFH	pHH	Reactive/unreactive
High translational energy	0.91	2.4	-7	-7	Unreactive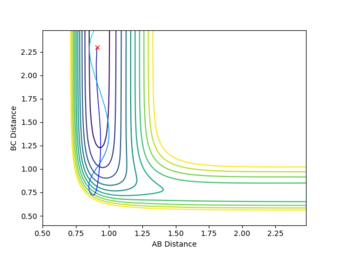
High vibrational energy	0.91	2.4	-0.1	-9	Reactive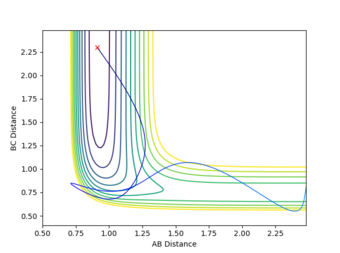

From the results generated it can be seen that an excess amount of translational energy would lead to the molecules hitting, and rebounding off the walls of the potential surface with no product formation. Whilst too much vibrational energy results in the molecules oscillating without reaching and exceeding the barrier

References

1) J. I. Steinfeld, J. S. Francisco, W. L. Hase Chemical Kinetic and Dynamics, Chapter 10, 297-310

2) P.Atkins and J. de Paula, Physical Chemistry, 10th Edition:2014