Results and Discussion Section:
Part 1: Day 1 and 2
INCLUDE DOI
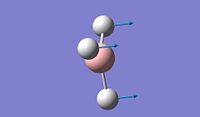
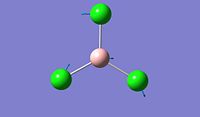
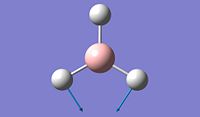
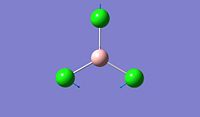
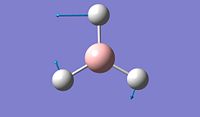
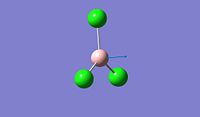
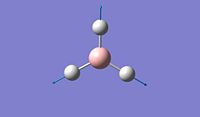
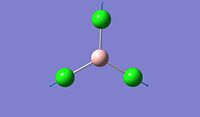
The objective of the first section is to be familiar with some techniques we can use in computational chemistry, especially via the software Gaussian. We first created a BH3 molecule using Gaussview 5.0 and then optimise the structure to find its lowest total energy, which referes to its most stable conformation. We then followed the same procedure for the BCl3 molecule and compare the obtained values for both molecules. Going into further details concerning the optimisation of these molecule, we proceeded firstly with the B3LYP basis set and then the LanL2MB options, which uses a medium level basis set. Moreover, the reason why we don't use basis sets is that they are more technical to implement and therefore, the calculation will take much longer. For this section, all optimisations are ran in the computer since the molecule are relatively small to allow the computational simulation to be done.
The following table summarizes the method used on Gaussview for the optimisations done. For our calculations on the computer, it generally took less than 30 minutes. Depending on the method and the basis set used, calculations on Gaussview will vary significantly.
| Calculation type | Calculation method | Basis set | |
|---|---|---|---|
| BH3 | FOPT | RB3LYP | 3-21G |
| BCl3 | FOPT | RB3LYP | LANL2MB |
BH3 BCl3
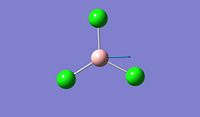
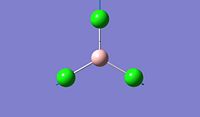
Optimised X-B-X bond angle (degree) 120 120 Optimised B-X bond distance (A) 1.18 1.86592

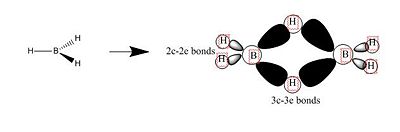
After optimisation, we found that for both molecule, the conformation which confers the lowest total energy is trigonal planar with X-B-X bond angle of 120°. In terms of bond distance, we notice a large difference between the B-H and the B-Cl bond lengths. The main reason for this observation is the presence of relatively high electronegative Chlorine atoms which effectively pull electrons away from the Boron nucleus and thus make the B - Cl bond shorter. However, what is seen experimentally can be rationalise in terms of molecular orbitals and thus stability. Indeed, unlike trihalides such as BCl3, borane compounds is not monomeric and usually dimerises to diborane. Molecular Orbitals theory can give an explantion for this observation. In diborane each boron is sp3 hybridised and forms normal 2-electron 2-centre (2e-2c) bonds with the terminal H atoms as well as 2-electron 3- centre (2e-3c) B-H-B bridging bonds.
 |
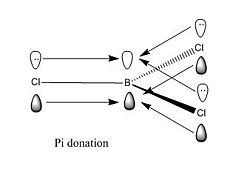 |
In the case of BCl3, an extra stability is present due to a pi donation from the lone pair in the 2p orbital of Cl to the empty 2p orbital on Sp2 B. This overlap effectively confers an extra stabilisation to the trihalide compound due to a good 2p - 2p overlap. However, when compared to the litterature, we notice that the value from the compatitional simulation is larger than the litterature value. This might be due to the extra stabilisation associated with the 2p - 2p orbital overlap making the B - Cl bond length slightly lower than expected. Indeed, the litterature value for B - Cl bond length is approximately 1.80 A, the computational simulation calculated a bond length of 1.86592 A. The difference arises the fact that computational chemistry cannot be perfectly accurate since it doesn't take account effect such as the previous one. Forthermore, concerning the bond angle, due to repulsion forces between Chlorine atoms, in the litterature, bond angles deviates slightly from 120 degrees. Again, computational chemistry predicted a perfect bond angle of 120 degrees. In other words, it calculates and determines the ideal situation for the molecule without taking account all factors which can affects the structure and the conformation in reality.
We then determined using Gaussian the molecular orbital of BH3 as well as BCl3. A Nbo calculation is carried out in order to obtain the charge distribution of both molecule and rationalise the previous prediction based on theory.
BH3 BCl3
Nbo charge on the ligand X (Debye) -0.110 -0.269 Nbo charge on the B central atom (Debye) 0.331 0.806

According to the script, the NBO analysis partitions the electron density of the whole molecule out into atomic like orbitals, which are then used to form 2e-2c bonds. As expected, we notice that the more electronegative the substituent, the more electropositive the central boron atom. Indeed, electronegative chlorine atoms tends to pull electrons away from the boron nucleus which makes it even more electropositive. The difference in charges for both compounds concerning the Boron central atom is significant. Furthermore, giving these informations about charges on both central boron atom and subtistuents, we can deduce information about the B - X bond strength with X = H, Cl.
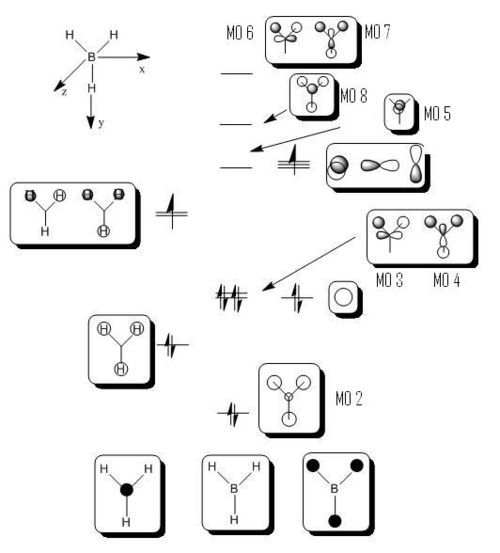
Calculations are ran in Gaussian in order to solve the electronic structure of both compounds and compute their molecular ortibals. We made sure that the method is set up to energy rather than optimisation and the additional keywords pop=full is added. For BH3 we took a snapshot of MOs 1 to 8, but only the HOMO and LUMO Molecular Orbitals for BCl3. They are all shown below:
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
We can then use the computed Molecular Orbitals to complete the final MO diagram of the trigonar planar BH3 compound. The difference between the real and LCAO MOs is small even if real MOs show the actual overlapping between orbitals and LCAO MOs don't. Furthermore, from it we can discuss about the accuracy and usefulness of qualitative MO theory. In fact, MO theory is a powerful tool for predictions, it however doesn't fully represent the real situation since theory usually refers to ideality. For the ground state structure, we expected from theory the symmetry of the molecule to be D3h according to the symmetry flow chart. It is actually the same used by Gaussview put as a symmetry constrain for BCl3.
In some structures gaussview does not draw in the bonds where we expect, however, it doesn't mean that there is no bond. First of all, we need to understand what is a bond. A bond is an interaction between atoms which allows the formation of polyatomic chemical compounds. Magnetic forces and dipole attraction induced by the presence of electrons and nuclei can explain their nature. Moreover, we can discuss about bonds in terms of molecular orbitals and therefore orbitals matching. A minimum of energy is required for a bond to be formed. However, Gaussview is a program which doesn't think. Indeed, it has a minimal energy and basis set for him to draw a bond or not. Since a bond cannot be rationalise completely in terms of minimal basis set, when gaussview does not draw in the bonds where expected, it doesn't give "real" information about the presence or absence of a bond. More specifically, we can manually draw the missing bond in cases where we can be confused. Additionally, for the symmetry of the molecule, we expected a D3h symmetry for the ground state structure. It appears that Gaussview found the same symmetry which effectively implies that the calculation made was right.
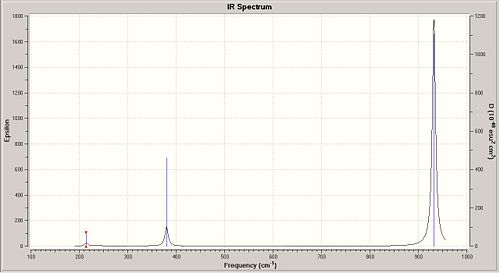
Finally, for the vibrational frequencies, we followed the same method as for the previous work done exept that we have chosen the job type " Frequency ". The calculation is done for both BH3 and BCl3.
The vibrational frequencies differs significantly between the BH3 and the BCl3 compounds. By looking at the IR wavenumbers, we notice that peaks for both B - Cl and B - H vibrations are seen in the fingerprint region (<500 cm-1). From the calculations there is also the Infrared Spectrum of the studied compounds.
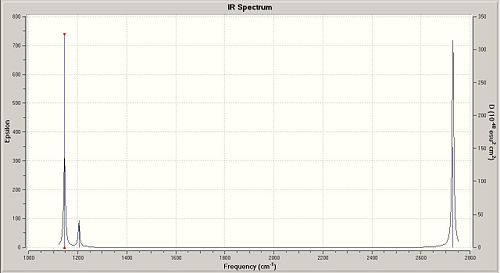
Part 2: Day 2 and 3
In this second part, we will start by optimising the ground state structures of two Mo(CO)4L2 isomers. We followed the instructions and obtained a structure in which the P - Cl bond doesn't appear on Gaussview. However, it doesn't mean that there is no bonds, the reason of this observation is that has an internal list of bond distances and if the computed bonds are outside of this Gaussview doesn't put them in. The purpose of optimising the ground state structure is to obtain good bond lengths and angles and thus the conformation lower in energy. This first optimisation is done using the B3LYP method associated to a low level basis LANL2B. The second optimisation require the conformation of both isomers to be slightly modified. We can then used the higher basis sets LANL2DZ for the optimisation. We obtained the following:

MO(CO)4L2 -Cis opt structure: https://www.ch.imperial.ac.uk/wiki/images/8/84/Log_18510_optimised_cis_Mo%28CO%294L2_SCAN.out MO(CO)4L2 -Trans opt structure: https://www.ch.imperial.ac.uk/wiki/images/b/b5/Log_18503_optimised_trans_Mo%28CO%294L2_SCAN.out
After obtaining the structures optimised via SCAN, we can now set up the calculations on Gaussview in order to submit the output file to SCAN and obtain the vibrational frequencies. We obtained the following:
MO(CO)4L2 -Trans vib freq: https://www.ch.imperial.ac.uk/wiki/images/2/27/Log_18522_log_18503_frequency_trans_Mo%28CO%294L2_SCAN.out
MO(CO)4L2 -Cis vib freq: https://www.ch.imperial.ac.uk/wiki/images/8/8d/Log_18527_log_18522_log_18503_frequency_cis_Mo%28CO%294L2_SCAN.out
The more stable isomer in terms of thermodynamics is the one with the lowest energy. According to the data from the computational simulation, it is found that the -cis conformation is the most stable and thus the most favourable one. However, the energy for both isomer are relatively similar, we therefore cannot determine which isomer is the most stable. The difference in energy observed is around 0.001 atomic unit which is effectively unsignificant.
Two factors could potentially alter the relative ordering of the cis and trans isomers, they are steric and electronic. Indeed, mainly by changing the nature and/or the size of the phosphorous atom, we can alter the ordering of the cis and trans isomer. For instance, if we replace the R group by phenyl groups, mainly due to steric clashes, the cis conformation won't be able to form easily and thus the most stable conformation would be -trans. On the other hand, if we want to favour the -cis conformation, we would then tend to put relatively small ligands such as hydrogen. Electronics can also alter the ordering of these isomers, and more specifically the nature of the substituent attached to the phosphorous atom. We can assumer from theory that the more electronegative the substituents, the shorter and the stronger the bonds. However in the -cis conformation, we can possibly have an important repulsion forces between the electronegative substituents which will relatively alter the ordering of the cis isomer. Consequently, to favour one isomer to another, the nature of substituents attached to the P atom is essential.
The CO stretches for both compounds are the last 4 vibrational frequencies. For the -trans isomer, they are seen at 1950.29, 1950.91, 1977.20 and 2030.99 cm-1. The CO stretches for the -cis isomer is seen at 1945.35, 1948.77, 1958.42 and 2023.40 cm-1.
Part 3: Mini Project
Introduction
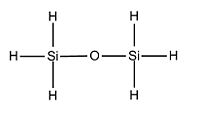
In this part of the module we will use the useful technique learnt in the previous sections on a specific case. Firstly we will optimise the structure to the lowest energy via the SCAN interface. We will then have a close look at the vibrational spectrum of the chosen molecules but also at their Molecular Orbitals in order to get a better understanding of their stability and reactivity. The chosen molecule for the mini project is a Silicon Dimer.
 |
 |
 |
 |
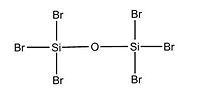 |
We have chosen Polyorganosiloxanes (silicones) compound for the mini project. By varying the nature of the substituent attached to the silicon atom and then by going down the group to replace the actual Si atom within the compound, we will carry out calculations in order to observe what is the actual effect of modifying substitients and the central atom on the total energy. Furthermore, Si- O - Si bond are observed to be relatively flexible mainly due to the delocalisation of the lone pairs on oxygen into available d orbitals on Si which effectively reduces the directionality of the Si–O bond and hence makes the structure more flexible. We will focus on the study of the silicon dimer by looking at its molecular orbitals, then carry out a Nbo analysis and finally calculate its vibrational frequencies in order to obtain a better understanding of its properties. Furthermore, since the modification of the ligands attached to the Si atoms can affect the Si - O bond strengh mainly due to the delocalisation of electrons, we may also carry out a Nbo analysis to observe how charges are distributed through le molecule.
We can make predictions for the actual effects of changing the ligands attached to the Si atoms. Firstly, by attaching to the Si atoms less electronegative atoms, the dimer will tend to be more bend in its conformation. The main reasons is the electron electron repulsion between the substituents and thus will tend to be as far as possible from each other. Furthermore, we can also predict that the Si - X bond length will increase going down the periodic table since the halogen atoms will be less electronegative. The ability to pull electrons away from the Si atom will therefore decrease making the bond longer and weaker in terms of energy. Variation within the vibrational frequencies will also be seen. Further analysis would be done using molecular orbitals as well as the Nbo method. On the other hand, we will also have a look at the effect of changing the nature of the central atoms (Si). Going down the periodic table, atoms effectively increases in size since the valence electrons found in orbitals have a higher n quantum nmber and hence a larger radii. This might affects significantly the conformation adopted by the dimer, the Y - O - Y bond angle with Y = Si, Ge etc and consequently its stability and flexibility.
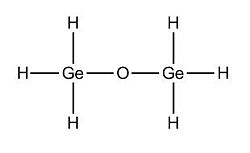 |
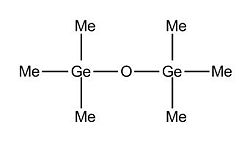 |
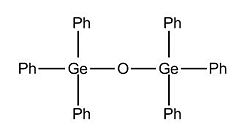 |
To summarize, during the mini project, we will look firstly at the effect on the conformation, bond angle and bond length with different electronegative substituents (halides). This study will mainly focus on electronic effects. We will then carry out calculations in order to determine the effect of the substituent's size on the previous parameters. Finally, we focused on the nature of the central atoms and notice the difference by going down the group with Si and Ge.
Results and Discussion
However, first of all, we will proceed to a full analysis of a dimer with hydrogen atoms as substituents attached to Si. The data for this dimer will basically be used as a reference for the rest of the calculations and analysis.

X (Si substituent) H
Si-O-Si Bond Angle (Degree) 179.994
Si-H Bond length (A) 1.50033
Si-O Bond length (A) 1.66857
After optimising the structure we obtained the previous conformation with a total energy of -654.39813776 atomic unit. In other word, the structure is relatively stable in terms of thermodynamics since there are no steric or electronic constrain. With this data we can't come to any conclusion, we thus need to compare these value with the ones determined in the next part of the project. We can carry out calculations to determine the molecular orbitals of the dimer, more specifically analyse the HOMO and LUMO and get a better understanding of the actual situation. The following pictures represents the HOMO, LUMO and MOs closed to it in energy.
(Si)2(H)6O Molecular Orbitals: https://www.ch.imperial.ac.uk/wiki/images/8/87/Si_MO.chk
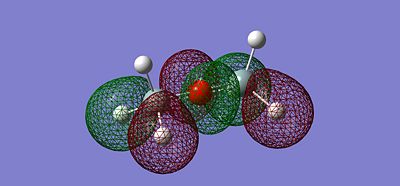 |
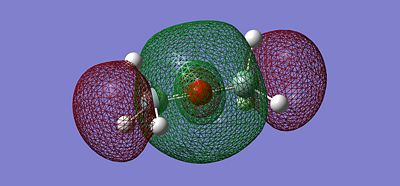 |
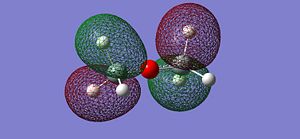 |
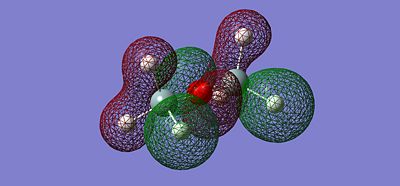 |
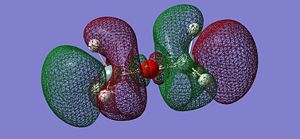 |
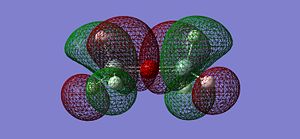 |
Running the Nbo calculation can help us understanding how charges are distributed trough the molecule. The balance in the charges allows the overall structure to be stable, especially with a Si - O - Si bond angle of approximately 180 degree. As expected, negative charges are concentrated mainly on the oxygen atom (-1.011) and due to the presence of the Si atom where most of the positive charge stand (1.109), hydrogen atoms are slightly electronegative (-0.201) to balance the overall charge of the molecule.
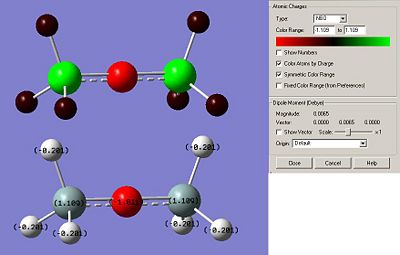
Finally, we determined the vibrational frequency for the molecule and followed the same method as the previous section. We focused on the Si - O vibrational frequency and stretching. The first Si - O - Si vibrational frequency is found to be 522.50 cm-1 and the second one 1173.09 cm-1. We compared these values to the litterature and notice that they are actually almost similar. Indeed, according to the litterature, the first vibrational frequency is meant to be 606.00 cm-1 and the second one 1107cm-1.
(Si)2(H)6O Vibrational Frequency: https://www.ch.imperial.ac.uk/wiki/images/3/3e/SiH_freq.out
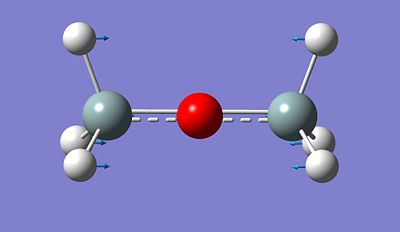 |
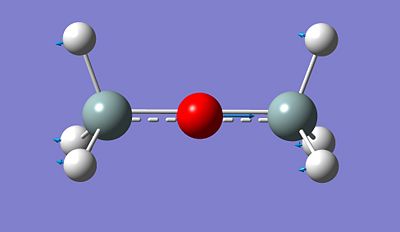 |
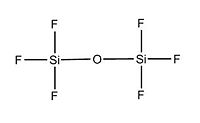
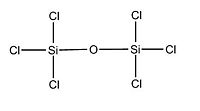
We will now focus on variation in the dimers conformation by increasing the electronegative nature of substituents attached to Si. Two optimisation process was done in order to obtain the following optimised conformations. Indeed, we followed the same procedure as for the -cis and -trans isomers of the previous section. We obtained from the calculation data the total energy of each dimers, as well as their Si - X bond length, Si - O bond length and Si - O - Si bond angle. According to the litterature, the Si-0-Si group is meant to be quasi-linear due to the large value of the Si-0-Si bond angle and that the Si-0-Si bending vibration may be highly anharmonic.
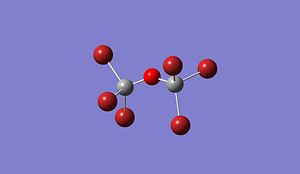 |
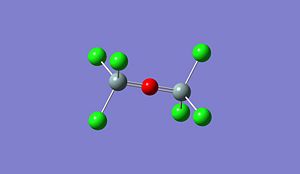 |
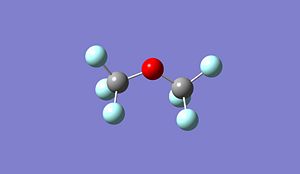 |
Optimised (Si)2(Cl)6O: https://www.ch.imperial.ac.uk/wiki/images/5/5c/Log_18809_si_cl_optimised_3.out Optimised (Si)2(Br)6O: https://www.ch.imperial.ac.uk/wiki/images/9/90/Log_18832_Si_Br_optimised_3.out Optimised (Si)2(F)6O: https://www.ch.imperial.ac.uk/wiki/images/2/24/Log_19069_Si_F_optimised_3.out
X H Br Cl F
Si-O-Si Bond Angle (Degree) 179.994 134.237 179.971 123.204
Si-X Bond length (A) 1.50033 2.00012 2.14241 1.37215
Si-O Bond length (A) 1.66857 1.40064 1.63998 1.40000
We notice that the dimer with Chlorine as substituent doesn't follow the trend in term of Si-O-Si bond angle and Si-O bond length either. Indeed, the more electronegative the substituent attached to Si, the more bend will be the molecule. Furthermore, as expected, as the electronegativity of the substituent increases, the Si - X bond length decreases. Indeed, since the halogen will tend to pull electron away from the Si nuclei, the bond length will be shorter and the bond stronger. We also predicted that the Si - O bond will be slightly affected, in fact, the bond get a bit smaller when increasing the electronegativity of the substituent. From this data, we can deduce a trend for the halogens: going down the periodic table for halogen atoms, the electronegativy is decreasing and thus the Si - O - Si bond angle will increase as well as the Si - X and Si - O bond length. We can for instance predict that if iodine atoms are attached to Si, the Si - O - Si bond angle will be higher than 134.237 degree and the Si - O bond length higher than 1.40064 A. This will give us an approximation on how flexible the Si - O - Si bond is. However, computational chemistry doesn't take account of all factors in reality so experimental data is required to confirm our hypothethis. Consequently, we can assume from the data that the Si - O - Si flexibility will tend to increase when substituent are less electronegative.
Vibrational frequency was run for all dimers but the informations from it wasn't analysed mainly due to time reasons. #
(Si)2(Br)6O vibrational frequency: https://www.ch.imperial.ac.uk/wiki/images/1/15/Si_Br_freq_3.out (Si)2(Cl)6O vibrational frequency: https://www.ch.imperial.ac.uk/wiki/images/5/5a/Si_Cl_freq_3.out (Si)2(F)6O vibrational frequency: https://www.ch.imperial.ac.uk/wiki/images/d/d0/Log_19073_Si_F_freq_3.out
Nbo calculations were run in order to confirm the distribution of charges within the molecule. It is a useful tool to confirm our hypothethis. We obtain the following:
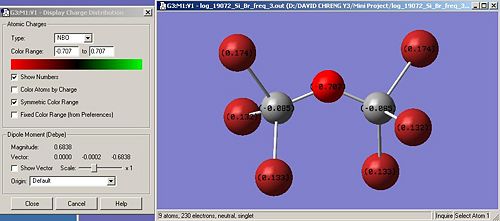 |
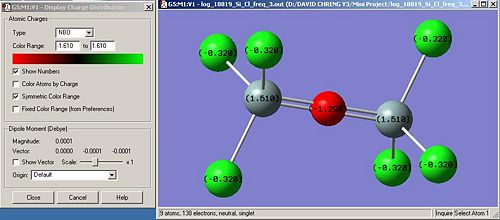 |
|
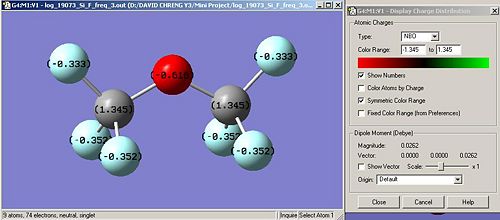
X H Br Cl F
Nbo on X (Debye) -0.201 0.174(1) 0.133(2) -0.320 0.333(1) 0.352(2)
Nbo on Si (Debye) 1.109 -0.085 1.610 1.345
Nbo on O (Debye) -1.011 -0.707 -1.298 -0.616
In terms of charges, the Nbo calculations confirms what was expected. Indeed, the more electronegative the atom attached to Si, in other words, going up the halogen row, the more positively charged the Si atoms and the less electronegatively charged the bridging oxygen atom. We can assume, following the trend deduced from our data, that if iodine atoms are attached to Si, the charge on Si will be higher 1.610 and on the bridging oxygen, higher than -0.707, thus more positively charged. However, we also notice a discontinuity in this trend regarding the Bromine atom.
Having looked at the electronic effect on the conformation of te dimer, the bond angle and bond length, we will know focus on the effect of sterics in the same parameters. Indeed, going from hydrogen atoms attached to Si to methyl and phenyl groups, we will proceed with the same methodology as before. However, for the phenyl substituents, only one optimisation has been done since it required too much computational ressources and thus take a relatively long amount of time.
(Si)2(H)6O Optimised Structure: https://www.ch.imperial.ac.uk/wiki/images/b/bd/Si_optimised_3.out (Si)2(Me)6O Optimised Structure: https://www.ch.imperial.ac.uk/wiki/images/f/f0/Si_Me_optimised_3.out (Si)2(Ph)6O Optimised Structure: https://www.ch.imperial.ac.uk/wiki/images/a/ac/Si_Ph_optimised_2.out
X H Me Ph
Si-O-Si Bond Angle (Degree) 179.994 179.994 179.951
Si-X Bond length (A) 1.50033 1.89338 1.95570
Si-O Bond length (A) 1.66857 1.68005 1.64396
Refering to the data, we observe that the size of the substituent doesn't affect the 180 degree Si - O - Si bond angle. Indeed, this conformation is the most stable since it allows the substituent to be as far as possible from each other to prevent steric hindrance and thus destabilisation forces. On the other hand, we notice that the more bulky the R group attached to Si, the longer the Si - R bond length adn thus the weaker it is. We can easily deduce that the more bulky the R group, the less flexible the Si - O - Si will be.
Finally, we tried to look at the effect of changing the Si atom by the Ge atom and see what effets it has on the previous studied parameters.
(Ge)2(H)6O Optimised Structure: https://www.ch.imperial.ac.uk/wiki/images/f/f4/Ge_optimised_3.out (Ge)2(Me)6O Optimised Structure: https://www.ch.imperial.ac.uk/wiki/images/c/cf/Ge_Me_optimised_3.out (Ge)2(Ph)6O Optimised Structure: DOI:10042/to-2826
However, we didn't have enough time to analyze the output files.
Key literature
http://article.pubs.nrc-cnrc.gc.ca/ppv/RPViewDoc?issn=1480-3291&volume=42&issue=11&startPage=2496