Results and Discussion:
1. The Hydrogenation of Cyclopentadiene Dimer
By using Chem3D, we defined the two dimers 1 and 2, and the two dihydro derivatives 3 and 4, then optimised their geometry by using the MM2 force field option. We obtained the following results:
Compound 1 2 3 4
Stretch: 1.2923 1.2454 1.2350 1.0916
Bend: 20.5870 20.8603 18.9699 14.5475
Stretch-Bend: -0.8413 -0.8320 -0.7617 -0.5461
Torsion: 7.6715 9.5039 12.1490 12.5089
Non-1,4 VDW: -1.4358 -1.5083 -1.5564 -1.0767
1,4 VDW: 4.2320 4.3012 5.7321 4.5041
Dipole/Dipole: 0.3778 0.4448 0.1632 0.1406
Total Energy: 31.8834 kcal/mol 34.0153 kcal/mol 35.9312 kcal/mol 31.1699 kcal/mol
 |
 |
 |
 |
The reaction observed is a peryciclic reaction, more specifically a [4n + 2] concerted reaction. Indeed, the Diels Alder reaction is stereospecific, so depending on the conformation of the dieniphile and the diene, we would produce specific isomers.
Refering to the litterature, Cyclopentadiene tends to dimerise into the endo dimer 2 rather than the exo dimer 1. However, by looking at the data collected from the simulation on Chem3D, we notice that the total energy of the endo dimer is lower than the exo one. In other words, the endo dimer is thermodinamically more stable than the exo dimer. We can therefore deduce that the cyclodimerisation of cyclopentadiene is kinetically controlled. By looking at both transition states, we notice that the endo Transition State is more stable than the exo one. Thus the kinetic product which predominates mainly due to the stability of its transition state. This stability is due to the interaction of the HOMO of the diene and the LUMO of the dienephile and allows the endo isomer transition state to be more stable and therefore the more favoured product.
Moreover, concerning the hydrogenation of the cyclopentadiene dimer, we notice that compound 4 has a lower total energy than compound 3. Indeed, the calculation shows that the dihydro derivative 4 is thermodynamically more stable than the dihydro derivative 3. We can thus deduce that the C=C double bond closer to the bridgehead carbon is easier to hydrogenate. By looking at the data, we also notice that in terms of bending, stretching, dipole-dipole and 1,4 Van Der Waals interaction, values for the dihydro derivative 3 are higher than for coumpound 4. Only the torsion and the non 1,4 non Van Der Waals interactions are higher for 4. This might have a small effect on the hydrogenation more likely to happen giving product 4.
2. Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD+ analogue)
By varying the geometry of the carbonyl group for the starting point in Chem3D, we effectively observe a change in the total energy. Furthermore, the geometry of the carbonyl group is directly related to the incoming MeMgI or PhNH2 in terms of reactivity. By looking at the mechanism of the reaction, we can understand why the methyl group has the stereochemistry shown in the final product. The high stereoselectivity for the addition of the Grignard reagent MeMgI is mainly due to a result of coordination between the Grignard reagent and the amide oxygen atom. In fact, depending on if the amide carbonyl group is above of coplanar with the plane of the amide ring, the intramolecular delivery of the Methyl group will effectively vary. Additionally, a variation in the total energy of the molecule is observed by using the Molecular Mechanics method in Chem3D. In other words, the lower the total energy found, the more stable in terms of thermodynamics and thus the more favourable the structure for the intramolecular delivery of the methyl group.

By starting with several starting points, in other words, with different bond angle for the amide carbonyl group, we effectively confirms what was expected theoretically. In fact, the carbonyl group directs the methyl group to attack in a specific direction. The negatively charged carbonyl group is attracted to the positively charged metal of the Grignard reagent. Therefore, depending of the position of the carbonyl group, the total energy of the molecule would vary since it implies selectivity. To obtain the most favourable conformation, the carbonyl group has to point up, thus it will direct the reaction by having an electrostatic interaction between the carbonyl group and the metal of the Grignard reagent.
|
|
 |
 |
 |
 |
By using Chem3D, we defined for the same molecule four different starting point in terms of structure, and then optimised their geometry by using the MM2 force field option. We obtained the following results:
1 2 3 4 5 6 Stretch: 1.3301 2.0425 10.7090 2.0557 2.0502 2.0751 Bend: 8.1668 14.1185 120.0887 14.1359 14.1337 14.1265 Stretch-Bend: 0.1209 0.1339 -2.7887 0.1335 0.1290 0.1369 Torsion: 13.7154 5.2238 32.6971 5.2222 5.2167 5.1527 Non-1,4 VDW: -1.6613 -0.6094 0.7797 -0.6047 -0.6211 -0.5595 1,4 VDW: 15.9645 16.5634 25.7263 16.5422 16.5576 16.5599 Charge/Dipole: 10.3436 9.3627 9.5126 9.3630 9.3771 9.3256 Dipole/Dipole: -3.8447 -3.9876 -2.5680 -3.9858 -3.9834 -4.0040 Total Energy: 44.1354 kcal/mol 42.8479 kcal/mol 194.1568 kcal/mol 42.8620 kcal/mol 42.8598 kcal/mol 42.8132
Several starting points for the optimisation have been used for this section in order to observe the effect of a change in the geometry of the carbonyl group and its orientation with respect to the aromatic group. Moreover, we also tried to vary the conformation of the aromatic ring and see the effect on the total energy of the molecule. As seen previously, since the carbonyl group is directly related to the incoming MeMgI, we notice that by varying the geometry of the carbonyl group and more specifically its dihydral bond angle, it effectively induces a slight change in the total energy.
Additionally, we looked at the dihedral angle for the amide carbonyl group and try to relate the angle value to the effective change in the total energy of the molecule and thus its stability toward nucleophilic attack. We obtained the following:
By looking at the dihedral angle calculated with Chem 3D, we notice that the angle closer to 22 degree refers to the most stable structure for the MeMgI nucleophilic attack. Indeed, we deduce that the dihedral angle with the amide carbonyl group has a major effect on the total energy of the starting material susceptible to nucleophilic attack. Indeed, as seen before, the amide carbonyl group effectively directs the incoming nucleophile and thus the reaction.
The second part of this section is about compound 7. The same procedure is followed by using several starting points and observe how modification on the structure and more specifically on the orientation of the carbonyl group affects the total energy of the molecule.
1 2 3 4
Stretch: 6.1195 3.6584 4.9868 5.7199
Bend: 18.5329 18.0013 64.7905 21.2425
Stretch-Bend: 0.5450 0.6832 -0.2743 0.4823
Torsion: 18.6265 -2.8949 39.3535 26.1153
Non-1,4 VDW: 7.0501 2.5071 -0.4618 5.3458
1,4 VDW: 29.6869 32.2214 40.5687 29.9944
Charge/Dipole: 9.4091 -- -- 3.3692
Dipole/Dipole: -4.9183 1.7546 0.8610 -4.7367
Total Energy: 85.0516 kcal/mol 55.9309 kcal/mol 149.8245 kcal/mol 87.5327 kcal/mol
 |
 |
 |
 |
Differences in the total energy are mainly due to modification done on the orientation of the carbonyl group relative to the nitrogen atom. Indeed, there is lone pair - lone pair repulsion between the carbonyl group and the nitrogen atom which destabilizes the structure and thus highers the total energy.
Key literature
- A. G. Shultz, L. Flood and J. P. Springer, J. Org. Chemistry, 1986, 51, 838. DOI:10.1021/jo00356a016
- Leleu, Stephane; Papamicael, Cyril; Marsais, Francis; Dupas, Georges; Levacher, Vincent. Tetrahedron: Asymmetry, 2004, 15, 3919-3928. DOI:10.1016/j.tetasy.2004.11.004
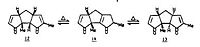
3. Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol
The most stable isomer will determine the stereochemistry of the carbonyl addition reaction, the carbonyl group is either pointing up or down. Again, we are using the Molecular Mechanics method to determine which isomer is the most stable by optimising the geometries via MM2. However, the minimum found is not necessarily the global minimum for the studied structure since the software only find a local minimum based on how close the starting structure is to the minimum one. We therefore had to start with several starting points in order to obtain the smaller total energy for both products.
By starting with compound 10 and minimizing the geometry, we obtained the following results. There is a variation in the total energy, it is mainly due to difference in the starting geometry of the compound.
 |
 |
 |
 |
1 2 3 4
Stretch: 2.8293 2.5488 2.7797 2.6397
Bend: 11.7283 11.1243 16.5093 15.8272
Stretch-Bend: 0.3907 0.7444 0.4344 0.3793
Torsion: 18.9590 12.8592 20.6315 18.3302
Non-1,4 VDW: -0.8334 -1.4218 -0.2707 -1.1326
1,4 VDW: 12.4116 15.5602 13.8676 12.7121
Dipole/Dipole: 0.1439 0.1664 0.1718 0.1461
Total Energy: 45.3490 kcal/mol 41.8620 kcal/mol 54.1236 kcal/mol 48.9020 kcal/mol
With the starting structure 1, 2 and 3, the main difference is on the orientation of the carbonyl group. Indeed, relative to the methyl groups attached to the carbone bridgehead, all three carbonyl groups are pointing up (same direction). However, the angle at which each carbonyl group differs from one to another. According to the data, we notice that the lower the total energy, the lower the stretch, the bend, the torsion, the non-1,4 Van Der Waals interations. On the other hand, the higher the 1,4 Van Der Waals interactions.
Additionally, to minimize the total energy, we also tried to modify the ring structure, by switching from the twist boat to the chair conformation. We nevertheless observe that the total energy went from 41.8620 kcal/mol (Structure 3) to 48.9020 kcal/mol (Structure 4). The difference in energy could be due to steric hindrances factors. Again, referring to the data, the torsion and the bend values are much higher for structure 4.
Furthermore, paying attention to the reaction with the alkene, we know that the alkene reacts relatively slowly. This can be explained with Bredt's rule. It refers to an empirical observation that states that a double bond cannot be placed at the bridgehead of a bridged ring system, unless the rings are large enough. Indeed, the low reactivity of the alkene is due to the hyperstability of the alkene. We can thus easily dedude that hyperstable alkene are very unreactive species, hence the observation on the rate of the alkene reaction. Moreover, the chair conformation of the six-membered ring is the most stable conformation. The larger the ring size, the more stable in terms of thermodynanics it is.
Key literature
- S. W. Elmore and L. Paquette, Tetrahedron Letters, 1991, 319; DOI:10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0
- See J. G. Vinter and H. M. R. Hoffman, J. Am. Chem. Soc., 1974, 96, 5466 (DOI:10.1021/ja00824a025 DOI:10.1021/ja00824a025 ) and 95, 3051 for another nice example of atropisomerism.
- Another well known example is within Vancomycin: J. Am. Chem. Soc., 1999, 121, 3226. DOI: 10.1021/ja990189i
- An interesting variation is of "atropenantioselective cycloetherification" (G.ÊIslas-Gonzalez, M.ÊBois-Choussy and J.ÊZhu, Org. Biomol. Chem., 2003, 30-32. DOI: 10.1039/b208905. See also Leleu, Stephane; Papamicael, Cyril; Marsais, Francis; Dupas, Georges; Levacher, Vincent. Tetrahedron: Asymmetry, 2004, 15, 3919-3928. DOI: 10.1016/j.tetasy.2004.11.004
4. Regioselective Addition of Dichlorocarbene
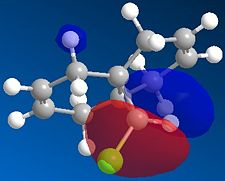
For the first part of the experiment, we will mainly focus on finding differences between the two alkenes double bond and more specifically find which one is the most nucleophilic. This is possible by looking at the HOMO of the two alkenes; the alkene double bond with the largest molecular orbital in terms of size is the most nucleophilic. Furthermore, in Chem3d, using the MM2 and then the MOPAC/PM6 method, we are then able to view specifically the HOMO-1, the LUMO, LUMO+1 and LUMO+2. Their pictures are shown below:
 |
 |
 |
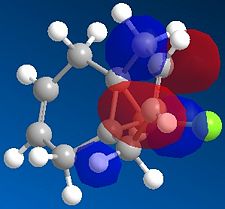 |
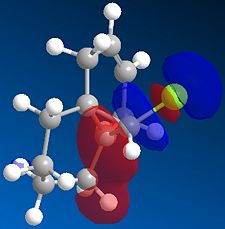
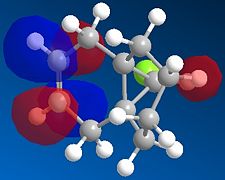
The representation of the HOMO -1 orbital of both alkenes in compound 12 clearly reveals that the double bond alkene closer to the C-Cl attached to the bridgehead carbon is bigger in size. In other words, we can easily deduce its most nucleophilic property. Indeed, we can see that according to the HOMO -1 picture, most of the electron density is obserded to be around the alkene double bond closer to the chlorine atom. Furthermore, this electron density is highly related to the vibrational frequency. Indeed as we will see in the next part of this section, differences are present between the starting compound and the hydrogenated product.
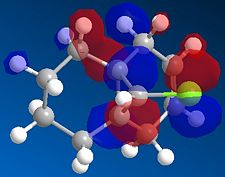
We then repeated the same procedure for the monoalkene with the remaining double bond on the same side as the Cl. We obtained the following:
 |
 |
 |
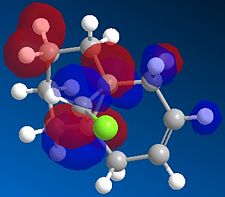 |
The representation of each molecular orbitals confirmed what was said before in terms of density of electrons being condensed into the alkene double bond.
Using Molecular Mechanics, we also defined the total energy of both molecules after optimizing its structure. The following table shows the data:
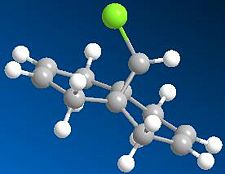 |
 |
1 2
Stretch: 0.6263 0.9246
Bend: 4.7930 4.6797
Stretch-Bend: 0.0417 0.0129
Torsion: 7.6092 10.7687
Non-1,4 VDW: -1.0565 -1.0843
1,4 VDW: 5.7844 6.9755
Dipole/Dipole: 0.1114 0.0705
Total Energy: 17.9095 kcal/mol 22.3476 kcal/mol
As predicted, the total energy of the starting compound (12) is lower than its hydrogenated product. In other words, it means that the compound is more stable in terms of thermodynamics. The overlap between the C=C π bonding and the C-Cl σ* anti bonding orbtal induces a overall further stabilisation to the molecule. The hydrogenation of the alkene double bond exo to the C-Cl bond prevents the molecule from this, hence the total energy is higher.
After optimizing the structure and submitting the file to SCAN, we can determine both Cl-C and C=C stretching vibrations in each system.
Starting compound Hydrogenated product
Vibrations: C=C (opposite to H) 1757.44 cm-1 1758.07 cm-1
C=C (opposite to Cl) 1737.01 cm-1
C-Cl 770.80 cm-1 774.98 cm-1
The vibration frequencies for both C=C and C-Cl are higher for the hydrogenated product which means that bonds are stronger. The main explanation for this observation is the presence of an extra alkene double bond, exo to the C-Cl bond. In fact, there is an overlap between the C=C π bonding and the C-Cl σ* anti bonding orbtal which induces a further stabilisation to the molecule, overall lowering the total energy of the molecule. However, on the other hand, a consequence of this further stabilisation is actually to lower the bond strengh of the C-Cl bond, hence the previous results.
Key literature
- B. Halton, R. Boese and H. S. Rzepa., J. Chem. Soc., Perkin Trans 2, 1992, 447. DOI:10.1039/P29920000447
5. Structure based Mini project using DFT-based Molecular orbital methods
|
|
For this last section, we have to find a reaction to study. The main sources we used was the Journal of Organic Chemistry, Organic Letters, Organic and Biomolecular Chemistry. We finally choose two isomers (compound 12 and 13) from the article A General Approach to Linearly Fused Triquinane Natural Products. Total Syntheses of (f)-Hirsutene,(f)-Coriolin, and (f)-Capnellene by Coverdhan Mehta,* A. Narayana Murthy, D. Sivakumar Reddy, and A. Veera Reddy. The two chosen isomers are diastereoisomers. In order to differenciate them, many spectroscopic techniques can be used such as 13C NMR, Infrared spectroscopy, or predicting the Optical Rotation. In our project, we will focus on the 13C NMR technique and compared the litterature values to the experimental data from computational simulation.
 |
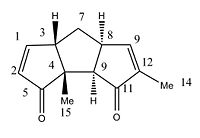 |
The interconvesion from isomer 12 to isomer 13 is thermally driven as seen in the picture below. The reaction is simpy an isomerisation.
Data from computational simulations
Compound 12 Compound 13
Shift (ppm) Degeneracy Atoms Difference* Shift (ppm) Degeneracy Atoms Difference*
199.2464000000 1.0000 4 9.6 203.4320000000 1.0000 5 8.27
198.4680000000 1.0000 10 9.14 199.8168000000 1.0000 11 7.19
176.5014000000 1.0000 1 12.4 178.2742000000 1.0000 1 12.77
174.9597000000 1.0000 9 15.25 175.2553000000 1.0000 10 15.45
130.0831000000 1.0000 11 11.1 131.2163000000 1.0000 12 8.99
121.6022000000 1.0000 2 9.9 118.3401000000 1.0000 2 11.26
60.4925000000 1.0000 5 0.3 60.6618000000 1.0000 4 3.56
60.3255000000 1.0000 3 0.82 57.5943000000 1.0000 3 1.09
60.1488000000 1.0000 8 2.64 55.3689000000 1.0000 9 1.88
50.5706000000 1.0000 7 3.27 52.5855000000 1.0000 8 0.92
31.4711000000 1.0000 6 0.57 38.7260000000 1.0000 7 7.78
27.4072000000 1.0000 14 5.8 29.1846000000 1.0000 15 7.72
17.8427000000 1.0000 15 7.74 17.7692000000 1.0000 14 1.23
Difference*: difference between the litterature values and the experimental data (computation simulations) in ppm.
Experimental data
Compound 12: 13C NMR (25.0MHz, CDC13): Chemical Shifts in ppm: 208.9, 207.6, 164.1, 159.7, 141.2, 131.5, 60.7, 59.5, 57.5, 47.3, 30.9, 21.6, 10.1
Compound 14: 13C NMR (25.0 MHz, CDC13): Chemical Shifts in ppm: 211.7, 207, 165.5, 159.5, 140.2, 129.6, 57.1, 56.5, 53.5, 46.5, 34.9, 19.0, 9.7
There is only a small difference between litterature values and experimental data. However, since computational simulations have limitations and more specifically cannot reproduce perfectly the reaction as well as the conditions/environment, there will be a slight deviation with experimental data found in laboratory. By looking at the J coupling values, we could be able to differenciate one isomer to the other.
 |
 |
However, the previous dihedral angle cannot be used to determine the 3J coupling value since the Karplus equation does not apply to system with a alkene double bond. We thus had to find another way of differenciating both isomers. Prediction of optical rotation can be used. The most efficient method would be NOESY (Nuclear Overhauser Effect Spectroscopy) which is a 3D NMR method based on spacial coupling between atoms rather than bond coupling. Since the geometry of some hydrogens differs from one isomer to another, by using this technique, we would actually be able to notice any differences in coupling through space.
Key literature
- Coverdhan Mehta,* A. Narayana Murthy, D. Sivakumar Reddy, and A. Veera Reddy, J. Am. Chem. SOC. 1986, 108, 3443-3452, 1986