Resgrp:comp-photo-benzene-tutorial
The Photochemical Isomerisation of Benzene to Benzvalene
Introduction
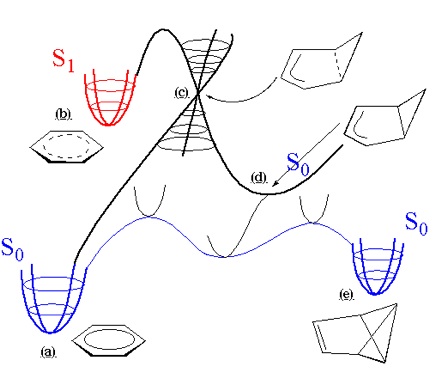
We shall study the valence isomeristion of benzene to benzvalene using CASSCF methods. There are many critical points on the S0 (singlet ground state), S1 (singlet first excited state), S2 (singlet second excited state) surfaces associated with the photochemical isomerisations of benzene. Here we only detail some points on the reaction path of benzene(a) to benzvalene(e).
This work is extract from the article :
An MC-SCF study of the S1 and S2 photochemical reactions of benzene, Ian J. Palmer, Ioannis N. Ragazos, Fernando Bernardi, Massimo Olivucci, and Michael A. Robb ; J. Am. Chem. Soc., 1993, 115 (2), 673-682
The starting geometry comes can come from your favourite molecular modelling package. Any similar package could also be used to generate the cartesian coordinates to start with.
The orbitals
We need initial orbitals for the CASSCF computation. The active orbitals shall be chosen from these molecular orbitals.
The orbitals we shall use are from a restricted Hartree-Fock calculation.
Calculation
So we need to calculate the orbitals of the molecule.
#p RHF/STO-3G Pop=Full Nosymm
Keyword Break
Nosymm keyword : We use the nosymm keyword because every time we run a calculation on the molecule with a different symmetry Gaussian reorients the molecule for that particular point group and will destroy the active space. Nosymm disables this feature.
pop=full keyword : Thus all orbitals are printed in the checkpoint file
Results
The CASSCF computation that we shall run will include 6 electrons in the 6 pn molecular orbitals. From the geometry used previously it can be seen that the pn M.O.’s are formed from pz atomic orbitals i.e. benzene is in the xy plane so we need the pz A.O.’.
Benzene has 42 electrons and since we are dealing only with the singlet manifold here there will be 21 and 21 electrons i.e. all electron spins are paired. There will be 21 occupied molecular orbitals.
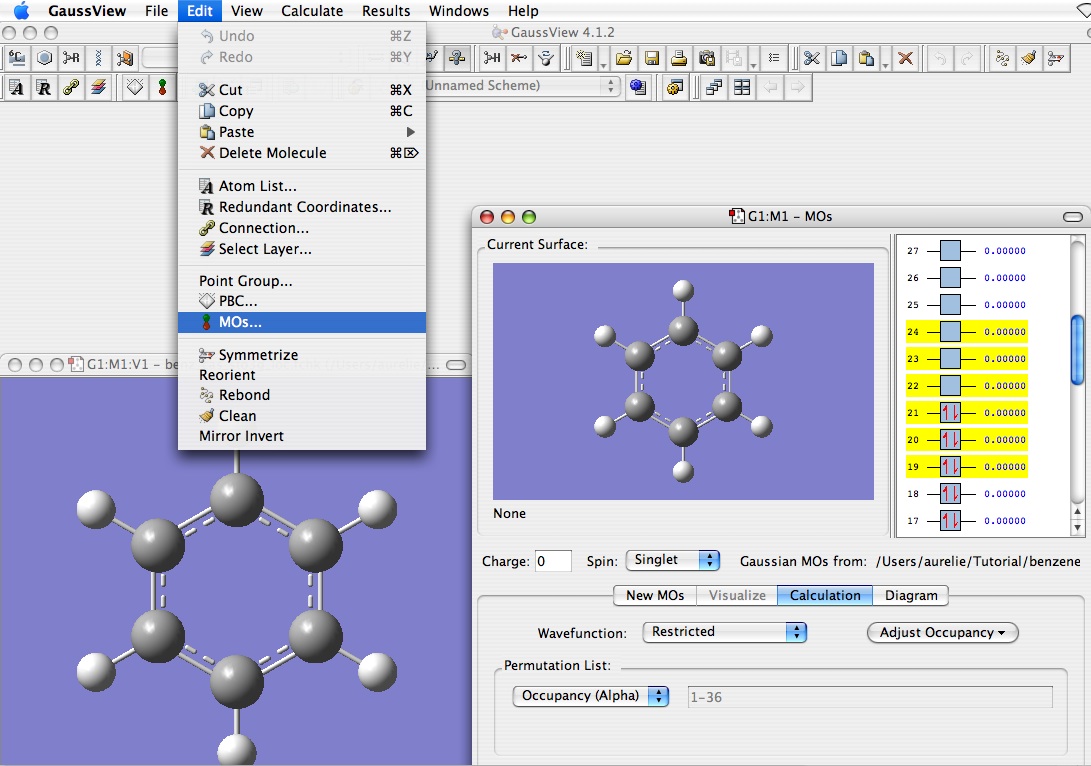
Access to the orbitals
Because the orbitals are in the checkpoint file, we need to convert the checkpoint file (which is normally binary) in order to enable GaussView to read these orbitals.
So in this aim, we use
-bash-3.00$ module load gaussian -bash-3.00$ formchk \work\username\namefile.chk \work\username\namefile.fchk
and it would formate the checkpoint file, that could be read by GaussView.
Then you just have to export the file and open with GaussView.
The number of electrons included in the active space are accommodated in the occupied orbitals. In this case there are six electrons in the active space so the occupied orbitals will be 19,20,21 (each accommodating two electrons). The remaining orbitals for the active space come from the virtuals. In this case for a CAS(6,6) orbitals 22,23,24 are the required orbitals. From the RHF calculation examination of the M.O.’s gives the pn orbitals as 17,20,21,22,23,24. Only orbital 17 is not included in the active space. We need to swap orbitals 17 and 19 to get the correct active space.
input and output fair
Media:benz_rhf.gjf
Media:benz_rhf.log
Orbitals with CASSCF
Calculation
#p CAS(6,6)/STO-3G Guess=(read,alter) Pop=Full Nosymm
Advice break
So we need to read the orbitals of the molecule, this information is in the .chk, so theoretically we need to ask the next calculation to read this checkpoint file.
Technically we need to copy this checkpoint file, because when you ask read the Checkpoint file in a calculation it changes the checkpoint file. In fact first Gaussian will read the checkpoint file to get the orbitals information, and then it will rewrite on the checkpoint file to create the new one. This means that in all subsequent jobs, the last .chk file must be copied, renamed and inputted in the %chk= line in the route section of the new .com file
So keep a safe version of each original checkpoint file, because if you did not this, if your calculation failed you will have to run again the first calculation to get a correct checkpoint file so as to read this one in the second calculation.
So copy and rename the checkpoint file to use it, or use the Mike's program
In order to check if the CASSCF calculation has been successful there are a number of tests that can be made.
1)The energy converges.
2) Orbital occupation numbers (diagonal elements of the density matrix) are not very close to zero or two (within three decimal places roughly). For the above calculation the occupancies are 1.95,1.87,1.87,0.13,0.13,0.05.
3) Localise the orbitals. The orbitals should localise onto atomic sites and can be checked with an orbital plotter (e.g. Gaussview) to verify that they are the correct orbitals to include in the active space.
So we can localise the orbitals :
#p CAS(6,6)/STO-3G Guess=read Pop=Full Nosymm IOp(5/42=1)
The localised orbitals are each an atomic pz orbital located on different atomic sites now. The occupation numbers of these orbitals are now exactly one.
Input and output fair
Media:benz_cas_sto3g.gjf
Media:benz_cas_sto3g.log
Media:benz_cas_sto3g_loc.gjf
Media:benz_cas_sto3g_loc.log
Optimise the geometry of the ground state minimum
STO-3G
First we have to optimise the geometry with the STO-3G basis set.
#p CAS(6,6)/STO-3G Guess=read Pop=Full Nosymm opt
The geometry is optimised in 3 steps.
Input orientation:
---------------------------------------------------------------------
Center Atomic Atomic Coordinates (Angstroms)
Number Number Type X Y Z
---------------------------------------------------------------------
1 1 0 0.000000 2.487816 0.000000
2 6 0 0.000000 1.405185 0.000000
3 6 0 0.000000 -1.405185 0.000000
4 6 0 1.216926 0.702592 0.000000
5 6 0 -1.216926 0.702592 0.000000
6 6 0 -1.216926 -0.702592 0.000000
7 6 0 1.216926 -0.702592 0.000000
8 1 0 2.154512 1.243908 0.000000
9 1 0 -2.154512 1.243908 0.000000
10 1 0 -2.154512 -1.243908 0.000000
11 1 0 2.154512 -1.243908 0.000000
12 1 0 0.000000 -2.487816 0.000000
---------------------------------------------------------------------
Break
Note now that Gaussian prints the symmetry of the optimised geometry as D2h and not D6h as it should be. This is because there is a small residual gradient component that breaks the symmetry (since we used the Nosymm keyword). The symmetry is not actually broken but equivalent cartesian coordinates are no longer the same to the required degree of accuracy for Gaussian to interpret the symmetry as D6h. This can be changed but is not necessary as inspection of bond lengths,angles etc. show that the geometry is of D6h symmetry.
Now the geometry can be optimised using a larger basis set. First project the STO-3G wavefunction onto a larger basis set.
4-31G
Run a single point at the STO-3G optimised geometry using a double zeta basis set(e.g. 4-31G).
#p CAS(6,6)/4-31G Guess=read Pop=Full Nosymm Geom=check
Now project the 4-31G wavefunction onto a larger basis set.
Run a single point energy calculation (again at this geometry) using a double zeta plus polarisation basis set (e.g. 6-31G*).
6-31G*
Break
It is important to do the above in two steps rather than projecting a STO-3G wavefunction straight onto a 6-31G* basis. This is too much change in the wavefunction for one step. A good rule of thumb is to project up one step at a time (either by increasing the split valence level or by increasing the highest angular momentum functions included in the basis set) e.g. STO-3G → 4-31G → 6-31G → 6-311G* → 6-311G** etc.
So now the S0 minimum geometry can now be reoptimised using a 6-31G* basis.
#p CAS(6,6)/6-31G(d) Guess=read Opt Pop=Full Nosymm
The geometry optimises in 3 steps again.
Input orientation:
---------------------------------------------------------------------
Center Atomic Atomic Coordinates (Angstroms)
Number Number Type X Y Z
---------------------------------------------------------------------
1 1 0 0.000001 2.471853 -0.000001
2 6 0 0.000000 1.396368 0.000000
3 6 0 0.000000 -1.396368 0.000001
4 6 0 1.209290 0.698184 0.000000
5 6 0 -1.209290 0.698184 0.000000
6 6 0 -1.209290 -0.698184 0.000000
7 6 0 1.209290 -0.698184 0.000001
8 1 0 2.140687 1.235927 0.000000
9 1 0 -2.140688 1.235926 0.000000
10 1 0 -2.140687 -1.235926 0.000000
11 1 0 2.140687 -1.235926 0.000000
12 1 0 0.000000 -2.471853 -0.000001
---------------------------------------------------------------------
The optimised C-C bond length is 1.3964Å and the C-H bond length is 1.0755Å.
Input and output fair
Media:benz_cas_sto3g_opt.gjf
Media:benz_cas_sto3g_opt.log
Media:benz_cas_431g.gjf
Media:benz_cas_431g.log
Media:benz_cas_631g_opt.gjf
Media:benz_cas_631g_opt.log
Calculate the S1 Frank-Condon vertical excitation energy
Calculation
The vertical excitation energies can be calculated from this optimised geometry.
Keyword break
You must include nroot=x in the CAS keyword === > Calculations on excited states of molecular systems may be requested using the NRoot option. (Note that a value of 1 specifies the ground state, not the first excited state)
#p CAS(6,6,nroot=2)/6-31G* Guess=read geom=check Pop=Full Nosymm
When calculating an energy difference between two states it is important to use the energy that is calculated using orbitals that are optimised for that state e.g. don’t take the S0 energy from a calculation of S1 as the orbitals then are not optimised for the S0 state. In order to calculate the S1 Frank-Condon vertical excitation energy take the S0 energy from the optimised 6-31G* S0 geometry.
The difference between these energies is 230.776453 — 230.593027 = 0.18462 Hartrees = 115.85 kcal mol-1.
Input and output fair
Media:benz_cas_s1_FC.gjf
Media:benz_cas_s1_FC.log
Investigate the S1 potential energy surface
We shall now investigate the S1 potential energy surface. We shall start an optimisation at the FC point.
This optimisation will be done in a 6-31G* basis. This is because we are close to an S1 minimum already.
Optimisation
#p CAS(6,6,nroot=2)/6-31G(d) Guess=read geom=check Pop=Full Nosymm opt
The geometry is optimised in 3 steps.
Input orientation:
---------------------------------------------------------------------
Center Atomic Atomic Coordinates (Angstroms)
Number Number Type X Y Z
---------------------------------------------------------------------
1 1 0 0.000000 2.507678 0.000000
2 6 0 0.000000 1.434449 0.000000
3 6 0 0.000000 -1.434449 0.000000
4 6 0 1.242269 0.717225 0.000000
5 6 0 -1.242269 0.717224 0.000000
6 6 0 -1.242269 -0.717225 0.000000
7 6 0 1.242269 -0.717224 0.000000
8 1 0 2.171713 1.253839 0.000000
9 1 0 -2.171713 1.253839 0.000000
10 1 0 -2.171713 -1.253839 0.000000
11 1 0 2.171713 -1.253839 0.000000
12 1 0 0.000000 -2.507678 -0.000001
---------------------------------------------------------------------
Frequencies calculation
A frequency calculation will tell us the nature of this critical point.
#p CAS(6,6,nroot=2)/6-31G(d) Guess=read geom=check Pop=Full Nosymm freq
All frequencies are positive so this corresponds to an excited state minimum.
1 2 3
A A A
Frequencies -- 295.4371 295.4372 488.0725
Red. masses -- 3.2296 3.2296 3.6249
Frc consts -- 0.1661 0.1661 0.5088
IR Inten -- 0.0000 0.0000 0.0000
This structure has D6h symmetry and corresponds to a redistribution of the electron system.
Input and output fair
Media:benz_cas_s1_631g.gjf
Media:benz_cas_s1_631g.log
Media:benz_cas_s1_631g_freq.gjf
Media:benz_cas_s1_631g_freq.log
Surface crossing regions between S0 and S1 ?
We shall now investigate any possible surface crossing regions between S0 and S1.
Since some of the experimentally observed photo-products are non-planar we should start with a non-planar structure. In order to achieve a slight deviation from planarity the z cartesian coordinate for atom one(H) is altered by setting it 0.6Å below zero(planar), atom two(C) 0.4Å below and atoms four(C) and five(C) 0.2Å below. This deviation is small enough that the previous active space can still be used, but this deviation is necessary to break the initial symmetry of the molecule.
This highlights the reason for always using the nosymm keyword as if symmetry was enabled the altered geometry would be reoriented and the active space could no longer be used.
STO-3G
So, now run an opt=conical with a STO-3G basis from this geometry. Use the .chk file from the calculation of the FC energy with the 6-31G(d) basis set.
1 .000000 2.471853 -.600001 6 .000000 1.396368 -.400001 6 .000000 -1.396368 .000000 6 1.209290 .698184 .200000 6 -1.209290 .698184 -.200001 6 -1.209290 -.698184 -.000001 6 1.209290 -.698184 .000001 1 2.140687 1.235927 .000002 1 -2.140687 1.235926 .000001 1 -2.140687 -1.235927 .000002 1 2.140687 -1.235926 -.000001 1 .000000 -2.471853 -.000001
#p CAS(6,6,nroot=2,nocpmcscf)/STO-3G Guess=read Opt=Conical Pop=Full Nosymm scfcon=6
Keyword break
The NoCPMCSCF keyword is included as this is an exploratory search and will make the calculation less expensive.
The above job should converge to an optimised conical intersection after 45 stepswith this coordinates :
Input orientation:
---------------------------------------------------------------------
Center Atomic Atomic Coordinates (Angstroms)
Number Number Type X Y Z
---------------------------------------------------------------------
1 1 0 0.284161 2.046427 -0.954452
2 6 0 0.141343 1.175129 -0.322597
3 6 0 -0.059215 -1.380876 0.026745
4 6 0 1.210498 0.758701 0.603881
5 6 0 -1.228899 0.640227 -0.145217
6 6 0 -1.302750 -0.735667 0.133509
7 6 0 1.101642 -0.484389 -0.181427
8 1 0 2.149607 1.302535 0.611529
9 1 0 -2.092941 1.261853 -0.340303
10 1 0 -2.233028 -1.259952 0.299490
11 1 0 1.971038 -0.868645 -0.706092
12 1 0 0.058544 -2.455342 -0.025066
---------------------------------------------------------------------
This shows that the starting geometry was far from the conical intersection geometry.
4-31G
Now run a single point energy calculation at this geometry with a 4-31G basis using state averaged orbitals.
#p CAS(6,6,nroot=2,stateaverage)/4-31G Guess=read Geom=check Pop=Full Nosymm scfcon=7
6-31G*
Finally run a conical intersection optimisation as before but with a 6-31G* basis from this geometry.
This should converge to an optimised conical intersection in 6 steps.
#p CAS(6,6,nroot=2,stateaverage)/6-31G(d) Guess=read Geom=check Opt=conical Pop=Full Nosymm scfcon=6
This should converge to an optimised conical intersection in 6 steps, with this coordinates :
Input orientation:
---------------------------------------------------------------------
Center Atomic Atomic Coordinates (Angstroms)
Number Number Type X Y Z
---------------------------------------------------------------------
1 1 0 0.319078 1.966089 -1.000563
2 6 0 0.135657 1.180314 -0.286969
3 6 0 -0.057305 -1.371640 0.020048
4 6 0 1.198682 0.752459 0.608500
5 6 0 -1.219120 0.636137 -0.150387
6 6 0 -1.295466 -0.734121 0.098932
7 6 0 1.100813 -0.487519 -0.145119
8 1 0 2.128665 1.292453 0.629601
9 1 0 -2.078395 1.262750 -0.299902
10 1 0 -2.218705 -1.253264 0.276505
11 1 0 1.922656 -0.804900 -0.764911
12 1 0 0.063440 -2.438757 0.014265
---------------------------------------------------------------------
Input and output fair
Media:benz_cas_s0s1_conical_sto3g.gjf
Media:benz_cas_s0s1_conical_sto3g.log
Media:benz_cas_s0s1_431g.gjf
Media:benz_cas_s0s1_431g.log
Media:benz_cas_s0s1_conical_631g.gjf
Media:benz_cas_s0s1_conical_631g.log
Optimising a ground state minimum starting from conical intersection geometry
Now we shall investigate some of the non-planar ground state valence isomers of benzene that could be connected to the previously optimised conical intersection.
We begin by optimising a ground state minimum starting from a geometry close to the conical intersection and therefore at first we have to use state averaged orbitals. There are several options that have to be set so that the correct stateaveraged gradient is used in the optimisation. Also, IOp(5/97=100) and IOp(10/97=100) need to be set in order that the state that is optimised is the ground state.
This calculation is done using CP-MCSCF and although this is more expensive because the basis set is only STO-3G overall it will not be too expensive.
First step : with stateaverage
Start at the 6-31G* optimised conical intersection and use an STO-3G basis. This geometry is displaced slightly from the STO-3G optimised conical intersection.
#p CAS(6,6,nroot=2,stateaverage)/STO-3G Guess=read Geom=check Nosymm scfcon=6 opt=calcall IOp(5/17=41000200,5/97=100) IOp(10/10=700007,10/97=100)
This should optimise to a critical point in 7 steps.
Input orientation:
---------------------------------------------------------------------
Center Atomic Atomic Coordinates (Angstroms)
Number Number Type X Y Z
---------------------------------------------------------------------
1 1 0 0.455245 1.758765 -1.158247
2 6 0 0.221508 1.009251 -0.411547
3 6 0 -0.065044 -1.373188 0.005057
4 6 0 1.167859 0.744902 0.712748
5 6 0 -1.223742 0.627081 -0.167001
6 6 0 -1.323281 -0.752821 0.076335
7 6 0 1.005825 -0.344711 -0.295187
8 1 0 2.083859 1.292065 0.905327
9 1 0 -2.039516 1.335579 -0.170844
10 1 0 -2.245753 -1.267450 0.305819
11 1 0 1.824662 -0.605423 -0.955114
12 1 0 0.138378 -2.424051 0.152653
---------------------------------------------------------------------
A check on the energy difference between S0 and S1 shows that it is high enough that the state averaging can be switched off.
Second step : without stateaverage
Reoptimise starting at the state averaged optimized geometry without any state averaging. Include IOp(1/8=5) to lower the stepsize since we are close to the critical point.
#p CAS(6,6)/STO-3G Guess=read Geom=check Opt Pop=Full Nosymm scfcon=6 IOp(1/8=5)
This should optimise in 4 steps, with this geometry
Input orientation:
---------------------------------------------------------------------
Center Atomic Atomic Coordinates (Angstroms)
Number Number Type X Y Z
---------------------------------------------------------------------
1 1 0 0.454514 1.759775 -1.156953
2 6 0 0.220791 1.009356 -0.411069
3 6 0 -0.065137 -1.373045 0.004628
4 6 0 1.167973 0.745055 0.712667
5 6 0 -1.223602 0.626849 -0.167402
6 6 0 -1.322654 -0.752420 0.076632
7 6 0 1.005497 -0.345341 -0.294534
8 1 0 2.084309 1.292286 0.903677
9 1 0 -2.039644 1.335007 -0.172022
10 1 0 -2.245073 -1.266958 0.306663
11 1 0 1.825167 -0.606435 -0.953372
12 1 0 0.137857 -2.424128 0.151087
---------------------------------------------------------------------
Frequencies
Before continuing by reoptimising in a larger basis it is useful to run a frequency calculation to examine the nature of this critical point.
#p CAS(6,6)/STO-3G Guess=read Geom=check Freq Pop=Full Nosymm scfcon=7
The results of the frequency calculation show that all (3N-6=33) frequencies are positive. This means that the point is a minimum on the STO-3G potential surface.
Frequencies -- 256.4323 345.8174 546.6439
Reoptimisation using a 6-31G* basis set
But before reoptimise using a 6-31G* basis, we have to run a 4-31G single point calculation.
#p CAS(6,6)/4-31G Guess=read Geom=check Pop=Full Nosymm scfcon=7
And then use the .chk file to run the next calculation :
#p CAS(6,6)/6-31G(d) Opt Guess=read Geom=check Pop=Full Nosymm scfcon=7
This should optimise in 8 steps, with the geometry :
Input orientation:
---------------------------------------------------------------------
Center Atomic Atomic Coordinates (Angstroms)
Number Number Type X Y Z
---------------------------------------------------------------------
1 1 0 0.453948 1.747802 -1.149419
2 6 0 0.213910 1.006540 -0.404986
3 6 0 -0.065991 -1.364380 -0.007856
4 6 0 1.166150 0.742352 0.692917
5 6 0 -1.216019 0.620580 -0.177893
6 6 0 -1.314469 -0.748706 0.062987
7 6 0 0.999374 -0.348743 -0.288753
8 1 0 2.068611 1.283273 0.904339
9 1 0 -2.025804 1.323234 -0.156360
10 1 0 -2.228478 -1.257251 0.307944
11 1 0 1.815240 -0.600681 -0.946150
12 1 0 0.133528 -2.404019 0.163230
---------------------------------------------------------------------
And then run again a frequency calculation.
#p CAS(6,6)/6-31G(d) freq Guess=read Geom=check Pop=Full Nosymm scfcon=7
But, now there is one imaginary frequency (negative sign in gaussian).
1 2 3
A A A
Frequencies -- -242.4766 347.7390 524.7518
This is an example where the STO-3G and the 6-31G* potential energy surfaces do not have the same topology. The structure below is actually a transition state on the S0 surface.
Input and output fair
Media:benz_cas_nonpln_s0_stavg_sto3g.gjf
Media:benz_cas_nonpln_s0_stavg_sto3g.log
Media:benz_cas_nonpln_s0_sto3g.gjf
Media:benz_cas_nonpln_s0_sto3g.log
Media:benz_cas_nonpln_s0_sto3g_freq.gjf
Media:benz_cas_nonpln_s0_sto3g_freq.log
Media:benz_cas_nonpln_s0_431g.gjf
Media:benz_cas_nonpln_s0_431g.log
Media:benz_cas_nonpln_s0_631g.gjf
Media:benz_cas_nonpln_s0_631g.log
Media:benz_cas_nonpln_s0_631g_freq.gjf
Media:benz_cas_nonpln_s0_631g_freq.log
Distorting the geometry and reoptimisation
By distorting the geometry in the direction of this imaginary frequency we can "go downhill" from the transition structure and find a minimum. The distortion is achieved by Fortran program which scales the transition vector and adds it to the transition state geometry. The program basically adds the normal mode of the transition vector (printed in Gaussian) to the geometry in cartesian coordinates after multipling the vector by a scale factor. This could also be done using a spreadsheet e.g. EXCEL.
Optimisation
The optimisation is done using a 6-31G* basis from the beginning now.
#p CAS(6,6)/6-31G(d) Opt Guess=read freq Pop=Full Nosymm scfcon=7
This should optimise in 30 steps.
Input orientation:
---------------------------------------------------------------------
Center Atomic Atomic Coordinates (Angstroms)
Number Number Type X Y Z
---------------------------------------------------------------------
1 1 0 0.474215 1.605934 -1.630871
2 6 0 0.296529 0.898486 -0.845207
3 6 0 -0.090004 -1.447308 -0.146677
4 6 0 0.700017 0.784448 0.528181
5 6 0 -0.799414 0.689214 0.167337
6 6 0 -1.200244 -0.766966 0.177478
7 6 0 0.977691 -0.400565 -0.360024
8 1 0 1.287503 1.381316 1.197460
9 1 0 -1.473708 1.489869 0.413817
10 1 0 -2.175984 -1.143934 0.412590
11 1 0 1.984351 -0.634699 -0.657136
12 1 0 0.044049 -2.505794 -0.251948
---------------------------------------------------------------------
Frequencies
Then run again a frequency calculation.
#p CAS(6,6)/6-31G(d) Guess=read freq geom=check Pop=Full Nosymm scfcon=7
There are now no imaginary frequencies.
1 2 3
A A A
Frequencies -- 523.0179 543.7006 618.1828
And finally inspection of the geometry shows that it is benzvalene.
Input and output fair
Media:benz_cas_s0_nonpln_dist_631g.gjf
Media:benz_cas_s0_nonpln_dist_631g.log
Media:benz_cas_s0_nonpln_dist_631g_fr.gjf
Media:benz_cas_s0_nonpln_dist_631g_fr.log