Introduction

The Transition State

According to Computational Quantum Chemistry the reaction coordinate was functionalised by all 3N_atoms-6 internal coordinates.

Potenyial energy surface describes the energy of a specific system where energy was tabulated by a set of reaction coordinates. [1]

The reactant and product with stationary structure are the minimum points on the potential energy surface.It could be calculated by :

Equation. 1 [1]

where R is a set of all internal coordinates and q is normal coordinates which is a linear combination of all internal coordinates.

The transition state is the point with the highest energy along the reaction pathway. The second derivative should be all positive except the one along the reaction coordinate. Thus it could be calculated as below.

Equation. 2 [1]

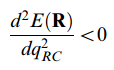
Nf710 (talk) 08:53, 23 March 2018 (UTC) You get this info by diagonalising the hessian matrix which is second derivatives in the basis of the degrees of freedom. the diagonalisation give the normal modes as eigenvectors and the force constants as eigenvalues.

The computational method

In this exercise, PM6 and B3LYP/6-31G(d) methods have been used to calculate the optimized structure of the reactants, products and the transition state. PM6 method is generally a faster method to give a rough approximation of the structure. A more precise optimization could be carried out by B3LYP with basis set of 6-31G(d) while it often takes quite a long time.

Freqrency check

All the normal modes for stationary structure ,thus the reactants and products, should have positive values as they represent the minimum energy points on the PES. For all the transition state structures, only 1 negative value should be seen. It is because when calculating from a harmonic oscillator with negative force constant (The negative value of the second derivative along the reaction coordinate), frequency was obtained as a imaginary number. The negative value in the frequency table thus illustrate the imaginary number (e.g. 526.7i).

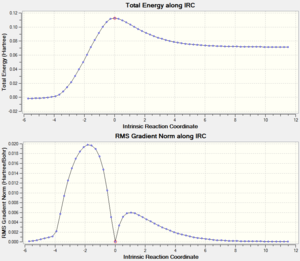
IRC check

IRC was obtained with the same basis set used to calculate the transition structrue. The gradient of the energy graph (thus the first derivative along the reaction coordinate) shows 0 at the Transition state, reactants and product, which confirms the success of obtaining transition state.

Nf710 (talk) 08:54, 23 March 2018 (UTC) This section was ok you could have done abit more reading and gone into more detail.

Exercise 1: Reaction of Butadiene with Ethylene

In exercise 1, the simplest Diels-Alder reaction between butadiene and ethene was calculated.

The net reaction was visualized by the bond length measurment which represent the change of bond order.

TS analysis

All reactants and product were optimized at PM6 level. Transition state were obtained at PM6 level with frequency checked to only have one negative value at around -930.

MO diagram for the formation of the butadiene/ethene transition state

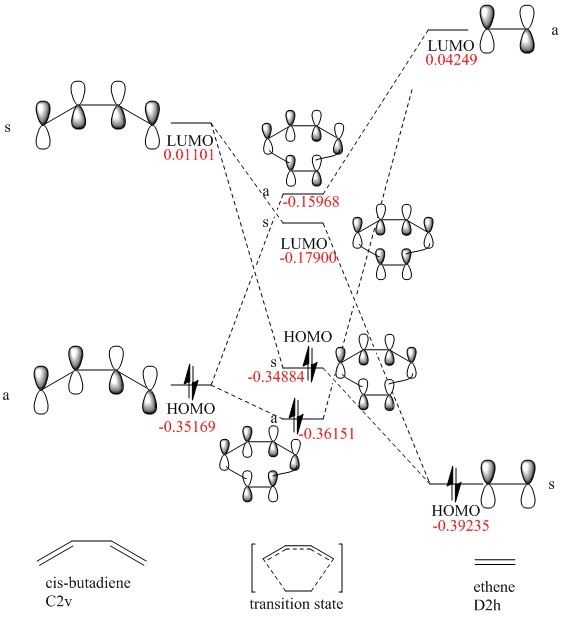
MO diagram for the formation of the cyclohexene

(Fv611 (talk) You did a good work in this exercise overall but you got a bit confused here in reporting the energies of your TS LUMOs. Both the LUMO and LUMO+1 are higher in energy than what you have used here in the diagram.)

The MO energy level of both reactant was obtained by Energy calculation using PM6 method. For this specific Diels-Alder reaction between butadiene and ethene with no substituents, the electrons are in normal demand (Diene being electron rich and ethene being electron poor).

The Transition state MO generated by both reactant has higher energy then the HOMO of ethene. That is due to the fact that it is MO for transition state (not the product) which is the highest energy point along the reaction pathway.

Visualised MOs for HOMO and LUMO

Table 1: Visualised MOs

cis-Butadiene

Ethene

Transition state

HOMO

LUMO

HOMO

LUMO

HOMO-1

HOMO

LUMO

LUMO+1

HOMO diene

LUMO diene

HOMO ethene

LUMO ethene

HOMO-1 TS

HOMO TS

LUMO TS

LUMO+1 TS

Correlation with MO diagram

For a reaction to take place the interacting orbitals must have the same symmetry (a-a/s-s), also both orbitals should be in the similar energy level. For both symmetric-symmetric interaction and antisymmetric-antisymmetric interaction, the overlap integral is non zero. For symmetric-antisymmetric interactions the overlap integral is zero.

Bond length measurement

The Van der Waals radii of carbon is around 1.7 Å. A typical sp3-sp3 carbon bond length is about 1.54 Å, and a typical sp2-sp2 carbon bond length is about 1.33 Å.

	cis-Butadiene	Ethene	Transition State	Product	Bond length	Bond order

C1-C2	-	-	2.11484	1.53580	decrease	forming
C2-C3	-	1.32731	1.38205	1.53764	increase	breaking
C3-C4	-	-	2.11485	1.53579	decrease	forming
C4-C5	1.33529	-	1.37977	1.49261	increase	breaking
C5-C6	1.46826	-	1.41113	1.33306	decrease	forming
C6-C1	1.33537	-	1.37972	1.49261	increase	breaking

At transition state, the partially formed bond length is about 2.11 Å, which is smaller than 2 times the van der Waals radii of carbon atom while still longer than a typical sp3-sp3 C-C single bond. That means the electrons from both atoms have been interacting (but yet to form a bond) at the transition state, after which the distance decreased to 1.54 Å indicating the formation of a sp3-sp3 carbon bond in the product.

Bond vibration at reaction path

As seen in this bond formation vibration, two bonds are forming synchronously.

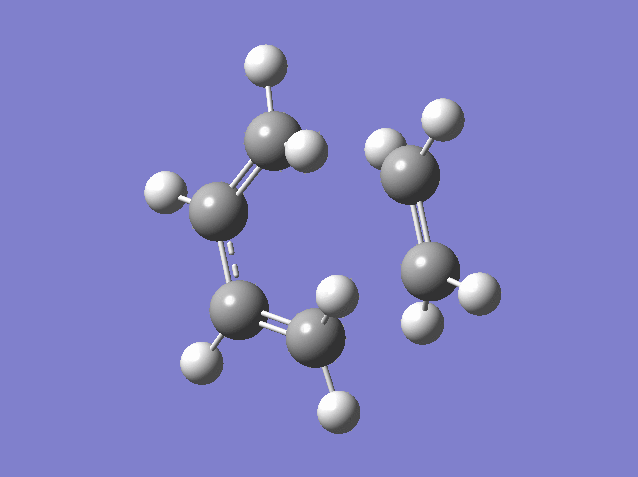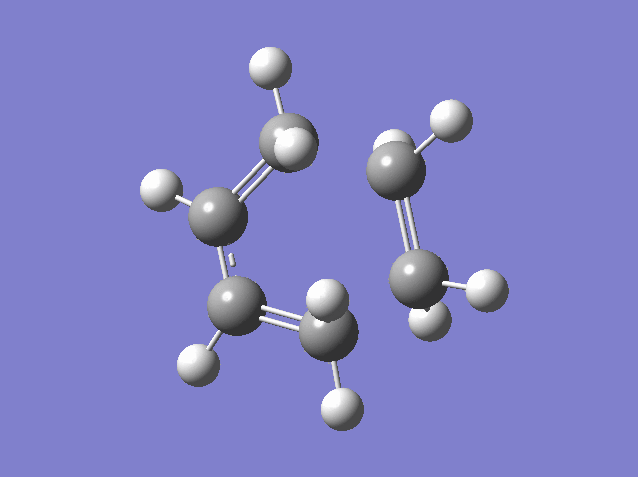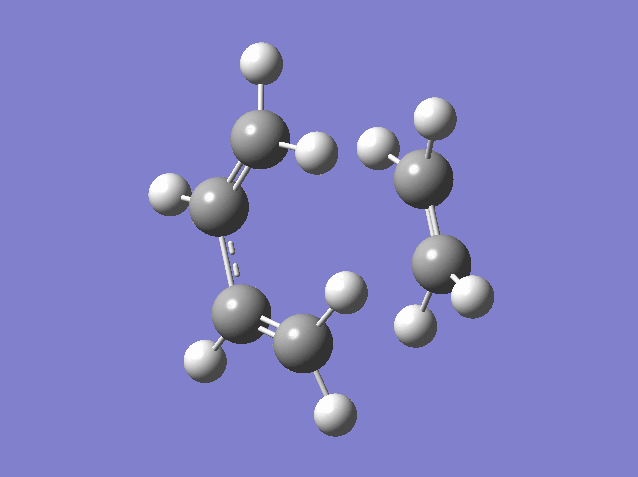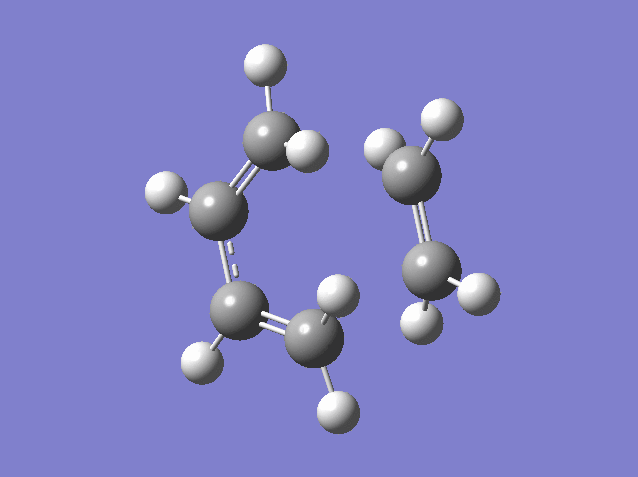
.log Files for Exercise 1

PM6 optimized s-cis-Butadiene: File:ZW4415 EX1 DIENE OPT PM6 4.LOG

PM6 optimized ethene: File:ZW4415 EX1 ETHENE OPT PM6.LOG

PM6 optimized transition state: File:ZW4415 EX1 TS OPT PM6 2.LOG

PM6 optimized product: File:ZW4415 EX1 PRODUCT OPT PM6.LOG

PM6 IRC: File:ZW4415 EX1 TS IRC PM6 2 2.LOG

Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole

This is a reaction between cyclohexadiene and 1,3-Dioxole. There are 2 pathways of Diels-Alder reaction, Endo and Exo. For both pathway, reactants, TS and products were approximated using PM6 method then reoptimized by B3LYP method with 6-31G(d) basis set. Frequencies were checked, Gibbs free energies were extracted and MO diagrams were constructed and adjusted.

Visualized HOMOs and LUMOs,frequency check and Gibbs free energies

(Fv611 (talk) You have compared PM6 optimised reactants with a B3LYP optimised transition state, so your MO diagrams are incorrect.)

HOMO

LUMO

frequency check

Gibbs Free Energy (Hatree)

Cyclohexadiene

HOMO Cyclohexadiene

LUMO Cyclohexadiene

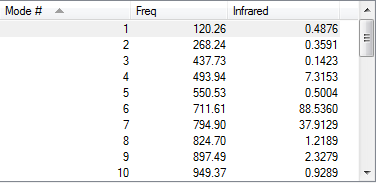
-233.324375

1,3-Dioxole

HOMO 1,3-Dioxole

LUMO 1,3-Dioxole

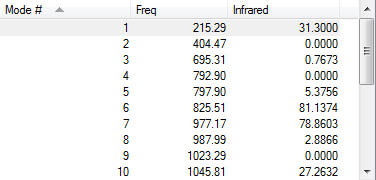
-267.068132

Exo transition state

HOMO Exo TS

HOMO-1 Exo TS

LUMO Exo TS

LUMO+1 Exo TS

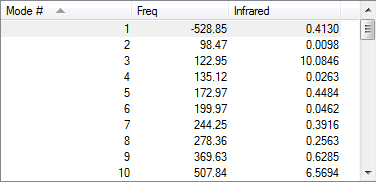
-500.329169

Exo product

-500.417322

Endo transition state

HOMO Endo TS

HOMO-1 Endo TS

LUMO Endo TS

LUMO+1 Endo TS

-500.332149

Endo product

-500.418692

According to the frequency calculation, all transition states are showing only 1 negative value and all the other species are showing all positive frequencies which confirms the success in obtaining the optimized structures.

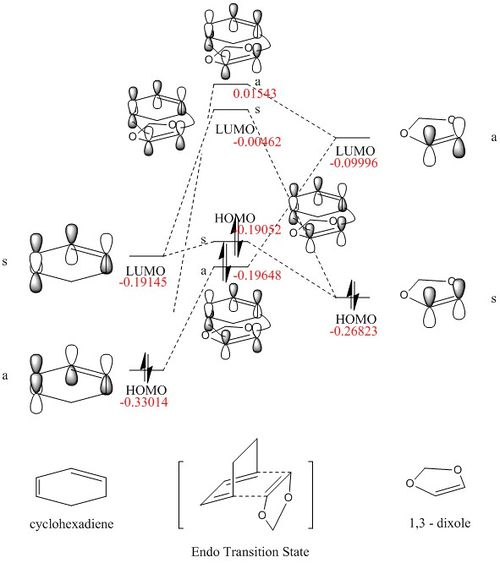
MO diagram

Firstly the a single point energy calculation was carried out for two reactants being separated for 20 a.u.(i.e. assume no interaction) The MO diagram for the resulting file was shown below

The value of the each energy level was used to draw the corresponded MO diagram. The energy levels for the MO of TS are higher than the final product as expected, as the TS represent the highest energy along the reaction coordination.

	EXO	ENDO
The MO diagram for TS formation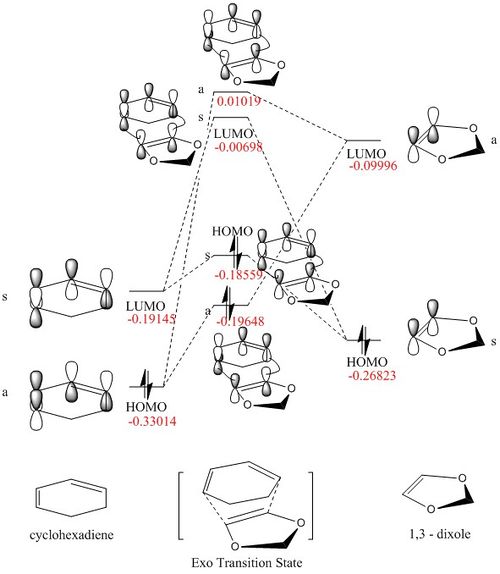
Reaction barriers (at room temp) / Hartree	0.062817 (164.926034 kJ/mol)	0.060358 (158.469929 kJ/mol)
Reaction energies (at room temp) /Hartree	-0.024815 (-65.1517825 kJ/mol)	-0.026185 (-68.7487175 kJ/mol)

The reaction barrier and reaction energy are both lower for the Endo-pathway. Therefore the endo pathway is both kinetic and thermodynamic favored.

From the single point calculation, the energy of the HOMO of the dieneophile (1,3-Dioxole) is higher than that of the diene (Cyclohexadiene) which shows that the dieneophile is more electron rich than the diene, thus inverse electron demand.

Nf710 (talk) 08:58, 23 March 2018 (UTC) Well done as long as these are optimised this should give you the right answer

Secondary orbital interactions

In the endo position, there are 2 oxygen p orbitals from oxygen lone pair which has the silimar energy and same symmetry of the cyclohexadiene LUMO, therefore they would have non-zero overlap integral. This interaction would lower the energy of LUMO producing a stabalising effect for the whole structrue. Thus more thermodynamically favored.

In the exo position, the two orbitals mentioned above were too far apart, thus almost no overlap integral. Moreover, there is a steric clash between the ring structure of 1,3-Dioxole and the half of the ring structure of cyclohexadiene, which rise up the energy of the net structure, thus less stable.

Nf710 (talk) 09:02, 23 March 2018 (UTC) This was a good section your study of the MO energies was particularly good.

.log Files for Exercise 2

B3LYP/6-31G(d) optimized cyclohexadiene:File:ZINAN WANG EX2 REACT1 OPT B3LYP.LOG

B3LYP/6-31G(d) optimized 1,3-dioxole:File:Zinan Wang EX2 REACT2 OPT B3LYP.log

B3LYP/6-31G(d) optimized Exo TS:File:ZINAN WANG EX2 TS EXO OPT B3LYP MO.log

B3LYP/6-31G(d) optimized Endo TS:File:ZINAN WANG EX2 TS ENDO OPT B3LYP CHRIS.LOG

B3LYP/6-31G(d) optimized Exo product:File:Zinan Wang EX2 PRODUCT EXO OPT B3LYP.log

B3LYP/6-31G(d) optimized Endo product:File:ZINAN WANG EX2 PRODUCT ENDO OPT B3LYP.LOG

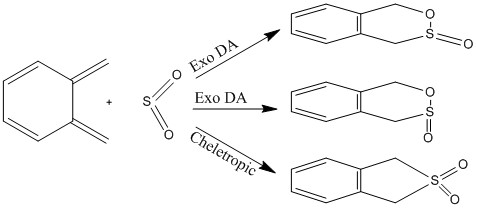
Exercise 3: Diels-Alder vs Cheletropic

In exercise 3, xylylene and SO₂ are used as the reactant. They could react through 3 pathways: Exo and Endo hetero-Diels Alder reaction or the Cheletropic reaction. Energy barrier and reaction energy for each pathway has been calculated and plotted.

Reaction energy calculation

The Gibbs free energy for each reactants, transition states and products were extracted form the .log file at 'Thermochemistry' section and converted to kJ/mol.

	Gibbs free energy (Hatree)	Gibbs free energy (kJ/mol)
Xylylene	0.178134	467.6908
SO₂	-0.118614	-311.4211
EXO TS	0.092078	241.7508
ENDO TS	0.090558	237.76
Cheletropic TS	0.099062	260.0873
EXO product	0.021456	56.33273
ENDO product	0.021696	56.96285
Cheletropic product	-0.000002	-0.00525

Reaction coordinations

	Exo DA reaction	Endo DA reaction	Cheletropic reaction
Reaction coordinate from IRC (click to see animation)
IRC energy calculation
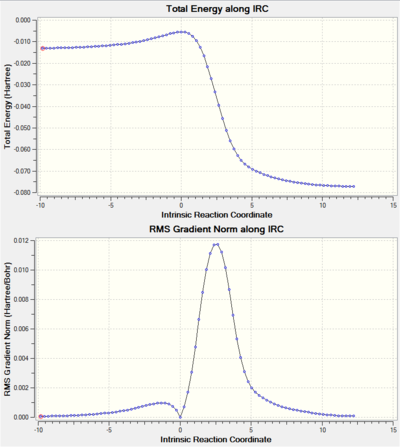
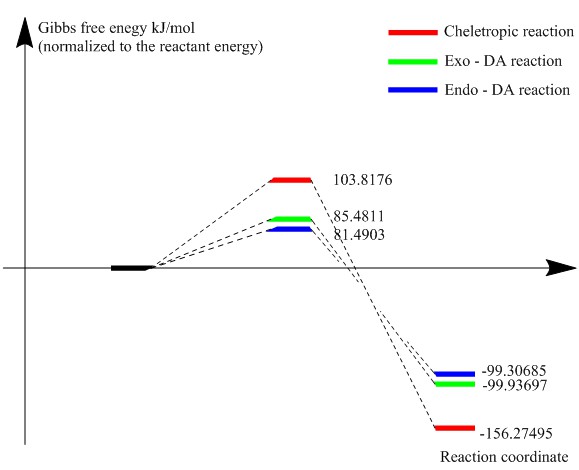
Reaction barriers (kJ/mol)	85.4811	81.4903	103.8176
Reaction energy (kJ/mol)	-99.9370	-99.3069	-156.275

From the reaction barriers calculated, the Endo path has slightly lower reaction barrier than the Exo path. These two DA reaction path also has the silimar reaction energy. Although the most kinetic path is the Endo, the Exo is a strong competing pathway.

The Cheletropic reaction has the highest reaction barrier while the lowest reaction energy, thus it is most thermodynamic favored.

(Too many significant figures. You need to think about the errors related to to the convergence criteria you are using Tam10 (talk) 15:03, 16 March 2018 (UTC))

.log Files for Exercise 3

PM6 Optimized Xylylene:File:ZINAN WANG EX3 REACT1 OPT PM6.LOG

PM6 Optimized SO2:File:ZINAN WANG EX3 SO2 OPT PM6.LOG

PM6 Optimized EXO product:File:ZINAN WANG EX3 P EXO OPT PM6.LOG

PM6 Optimized EXO TS:File:ZINAN WANG EX3 TS EXO PM6.LOG

PM6 Optimized ENDO product:File:ZINAN WANG EX3 P ENDO OPT PM6.LOG

PM6 Optimized ENDO TS:File:ZINAN WANG EX3 TS ENDO PM6.LOG

PM6 Optimized Cheletropic product:File:ZINAN WANG EX3 P CHELE OPT PM6.LOG

PM6 Optimized Cheletropic TS:File:ZINAN WANG EX3 TS CHELE PM6.LOG

Conclusion

In this computational lab, 3 pericyclic reactions were investigated. Gaussian was used to optimized the structure of the reactants, products and transition states using either PM6 or B3LYP method with IRC and frequency checked to confirm the transition states. Gibbs free energy was extracted from the log file for each species and the reaction barriers and reaction energies were calculated from them. The kinetic favored pathway were determined by the lowest reaction barrier and thermodynamic favored pathway was determined by the lowest reaction energy.

This computational method could be carried out for more reactions to determine the reaction route under different conditions.

Reference

[1] J. J. W. McDouall, in Computational Quantum Chemistry: Molecular Structure and Properties in Silico, The Royal Society of Chemistry, London, 2013, ch. 1, pp. 1-62.