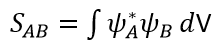Rep:Yrt13 TS
Introduction
In your introduction, briefly describe what is meant by a minimum and transition state in the context of a potential energy surface. What is the gradient and the curvature at each of these points? (for thought later on, how would a frequency calculation confirm a structure is at either of these points?) 1
In the following exercises, the reaction pathways of several Diels-Alder reactions and their transitions states will be studied. A Diels-Alder reaction is a pericyclic reaction between a conjugated diene and a dienophile. Specifically, it is a [4+2] cycloaddition involving rearrangement of π bonds. Reaction pathways can be studied by investigating a potential energy surface. 1
On a potential energy surface, the reactants and products correspond to the minimum points. A transition state is then identified as the maximum on the minimum energy pathway linking the reactants and the products. This is also known as a saddle point. Since the reactants, products and transition states lie on stationary points, the total gradient of the potential energy surface will be zero at these points. Therefore, the first derivative of the Potential Energy vs Bond Distances graph (gradient), ∂V(ri)/∂ri = 0
To differentiate between minimum points (reactants and products) and saddle points (transition states), we need to look further and consider their vibrational frequencies. Linear molecules have 3N - 5 normal vibrational modes / degrees of freedom while non-linear molecules have 3N - 6 normal vibrational modes, where N = the number of atoms the molecule has. Under the harmonic oscillator model, each vibrational mode has a restoring force F. This restoring force F is defined by Hooke's Law, F = - kx, where 'k' is the force constant and 'x' is the displacement from equilibrium position / extension from equilibrium length.
Since the force is the negative derivative of the potential energy function, F = - ∂V(ri)/∂ri = 0. Also, k = - ∂F(ri)/∂ri = (∂2V(ri)/∂ri2), the second derivative of the potential energy function. The value and sign of k reveals the nature of the stationary point. For example, k is positive at a minimum point while k is negative at a maximum point. The value and sign of k is also significant as frequency calculations involve taking the square root of k.
Since the reactants and products sit in a minimum well, the second derivative of the potential energy function (k) is positive in every degree of freedom as all degrees of freedom / coordinates are minimised. Therefore, reactants and products only have positive and real frequencies and will remain at this minimum 'forever' unless sufficient energy is provided for them to overcome reaction barriers.
The transition state, however, has a different mode of vibration along the reaction coordinate. Since the transition state lies on a saddle point (maximum on the minimum energy pathway), the second derivative of the potential energy function (k) is positive in every degree of freedom except one. This is because all other coordinates are minimised except along the reaction coordinate. Therefore, the transition state will have (only) one imaginary frequency, resulting from the one negative k. 1
Thus, the calculation of the second derivative of the potential energy surface (k) can be used to distinguish the reactants/products from the transition states.
Two main optimisation methods were used in the following exercises. Firstly, the semi-empirical method PM6 was first used to optimise all reactants, products and transition states. PM6 was used as a first optimisation step as it is a fitted method that uses experimental data in order to save time and resources during calculation, hence it is not as accurate.
Some of the reactants, products and transition states were then further optimised using the Density Functional Theory (DFT) method B3LYP/6-31G(d). The B3LYP method is reasonably fast and is capable of reproducing chemical data. Thus, it produces more accurate results, at the cost of computational effort.
Nf710 (talk) 00:12, 8 November 2017 (UTC) Excellent intro. Everything explained well. A few points you could have elaborated on how each degree of freedom is a normal mode, which is a linear combination of all the individual bends/rotation/bond lengths. hence why when you look at the vibration it looks like the whole molecule. You could have also gone into mmore detail about how the Quantum chemical methods work.
Exercise 1
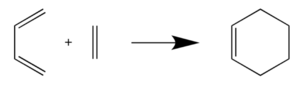
In this exercise, the [4+2] cycloaddition reaction of butadiene with ethylene, to yield cyclohexane as a product, was studied. In this reaction, butadiene acts as the diene while ethylene acts as the dienophile. The reactants, transition state and product were optimised at the PM6 level. IRC and frequency calculations were also done with the transition state.
Figure 1: Reaction scheme of Butadiene with Ethylene to form Cyclohexane. Adapted from https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:ts_exercise#Exercise_1:_Reaction_of_Butadiene_with_Ethylene
MO Diagram
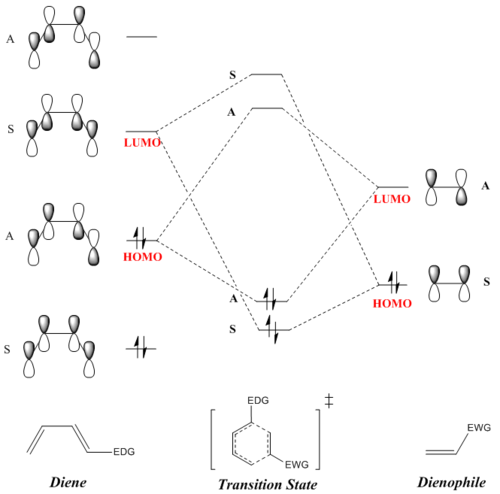
Construct an MO diagram for the formation of the butadiene/ethene TS, including basic symmetry labels (symmetric/antisymmetric or s/a).
Figure 2: MO Diagram for the formation of the butadiene/ethene TS. Note: This is the estimated MO diagram and energy calculations done at the PM6 Level were not used.
The symmetry labels 'S' (symmetric) and 'A' (anti-symmetric) correspond to the symmetry of the molecular orbitals (MO) with respect to the mirror plane perpendicular to the sigma bond at the middle of the MO.
HOMO/LUMO of Butadiene and Ethylene
| LUMO
of Butadiene |
LUMO
of Ethylene |
||||||
|---|---|---|---|---|---|---|---|
| HOMO
of Butadiene |
HOMO
of Ethylene |
Figure 3: Jmols of the HOMOs and LUMOs of Butadiene and Ethylene.
Four MOs produced at the Transition State
| MO16
of TS (A) |
MO17
of TS (S) |
||||||
|---|---|---|---|---|---|---|---|
| MO18
of TS (S) |
MO19
of TS (A) |
Figure 4: Jmols of the 4 relevant Transition State MOs.
(Fv611 (talk) 11:20, 2 November 2017 (UTC) Your MO is very good, although you could have pointed out which orbitals are the HOMO and LUMO of the Transition State.)
Questions
1. What can you conclude about the requirements for symmetry for a reaction (when is a reaction 'allowed' and when is it 'forbidden')?
For a reaction to be allowed, the symmetry of the orbitals must be the same (i.e. both must be symmetric or anti-symmetric). If one of the orbitals is symmetric while the other is anti-symmetric, the reaction is 'forbidden'.
The extent of orbital overlap between two orbitals (A and B) can be quantified by the overlap integral (SAB) 2. It is defined as:
If the product of both wavefunctions is symmetric, the overlap integral SAB is non-zero and the reaction is allowed. If the product of both wavefunctions is antisymmetric, SAB is zero and the reaction is forbidden.
2. Write whether the orbital overlap integral is zero or non-zero for the case of a symmetric-antisymmetric interaction, a symmetric-symmetric interaction and an antisymmetric-antisymmetric interaction.
| Interaction | Orbital Overlap Integral |
|---|---|
| Symmetric-Antisymmetric | Zero |
| Symmetric-Symmetric | Non-Zero |
| Antisymmetric-Antisymmetric | Non-Zero |
Table 1: Summary of Orbital Overlap Integral with respect to Interaction type.
Measurements
C-C Bond Lengths of Reactants
| Butadiene | Bond | C1-C4 | C4-C6 | C6-C8 | ||
|---|---|---|---|---|---|---|
| Bond Distance | 1.33530 Å | 1.46835 Å | 1.33530 Å |
Table 2: Summary of Bond distances in Butadiene.
| Ethylene | Bond | C1-C4 | ||
|---|---|---|---|---|
| Bond Distance | 1.32731 Å |
Table 3: Summary of Bond distances in Ethylene.
C-C Bond Lengths of Transition State
| Transition State | Bond | C1-C4 | C4-C6 | C6-C8 | C8-C11 | C11-C14 | C14-C1 | ||
|---|---|---|---|---|---|---|---|---|---|
| Bond Distance | 1.37977 Å | 1.41111 Å | 1.37977 Å | 2.11473 Å | 1.38176 Å | 2.11473 Å |
Table 4: Summary of Bond distances in the Cyclohexene Transition State.
C-C Bond Lengths of Product, Cyclohexene
| Cyclohexene | Bond | C1-C4 | C4-C6 | C6-C8 | C8-C11 | C11-C14 | C14-C1 | ||
|---|---|---|---|---|---|---|---|---|---|
| Bond Distance | 1.50084 Å | 1.33696 Å | 1.50081 Å | 1.53712 Å | 1.53459 Å | 1.53714 Å |
Table 5: Summary of Bond distances in the Cyclohexene Product.
Questions (continued)
3. How do the bond lengths change as the reaction progresses?
| Bond | C1-C4 | C4-C6 | C6-C8 | C8-C11 | C11-C14 | C14-C1 |
|---|---|---|---|---|---|---|
| Bond Distance Changes | Increases | Decreases | Increases | Decreases | Increases | Decreases |
Table 6: Summary of Changes in Bond distances (as reaction progressed).
In particular, the bond length between C1-C14 (and between C8-C11) changes the most due to the formation of the new C-C bonds. The bond length is originally 3.40 Å (twice the Van der Waals radius of C) 3
Figure 5: Plot of the Bond Distance (between C1 and C14) against Intrinsic Reaction Coordinate.
4. What are typical sp3 and sp2 C-C bond lengths? 4
Typical sp3-sp3 C-C bond length: 1.54 Å
Typical sp3-sp2 C-C bond length: 1.50 Å
Typical sp2-sp2 C-C bond length: 1.34 Å
5. What is the Van der Waals radius of the C atom? How does this compare with the length of the partly formed C-C bonds in the TS.
Van der Waals radius of the C atom: 1.70 Å.3 Twice the Van der Waals radius = 3.40 Å.
The length of the partly formed C-C bonds in the TS (C8-C11 and C14-C1) is about 2.11 Å. The length of the partly formed C-C bonds is shorter than twice the length of the Van der Waals radius (3.40 Å). This suggests that the C-C bonds are indeed forming.
(Fv611 (talk) 11:20, 2 November 2017 (UTC) The reasoning is incomplete here: what tells you that the bonds are forming is that the TS bond length is in between twice the Van der Waals radius and the length of a single C-C bond.)
The length of the other 4 C-C bonds (C1-C4, C4-C6, C6-C8 and C11-C14) are between 1.34 Å (typical sp2-sp2 C-C bond length) and 1.54 Å (typical sp3-sp3 C-C bond length). This is because the nature of the C-C bonds are changing (from C-C single bond to C=C double bond, or vice versa).
6. Illustrate the vibration that corresponds to the reaction path at the transition state. Is the formation of the two bonds synchronous or asynchronous?
Figure 6: Illustration of the vibration that corresponds to the reaction path at the transition state.
A concerted process5 (such as the Diels-Alder reaction) is synchronous when the changes concerned (in this case, bond formation) progresses to the same extent at the transition state. As seen from the Jmol, both bonds are formed at the same rate. Hence, this is synchronous.
Exercise 2
In this exercise, the Diels-Alder reactions of Cyclohexadiene and 1,3-Dioxole to form the Endo and Exo product were studied. Cyclohexadiene acts as the diene while 1,3-Dioxole acts as the dienophile. The reactants, transition states and products were first optimised at the PM6 level. The initial geometries generated at the PM6 level were then further optimised at the B3LYP/6-31G(d) level. Frequency calculations were executed on all reactants, transition states and products. The reactants (cyclohexadiene and 1,3-dioxole) and the exo and endo products had no imaginary frequencies. Both the exo and endo transition states had 1 imaginary frequency each. IRC calculations were done on both transition states as well.
Figure 7: Reaction scheme of Cyclohexadiene and 1,3-Dioxole. Adapted from https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:ts_exercise#Exercise_2:_Reaction_of_Cyclohexadiene_and_1.2C3-Dioxole
Using your MO diagram for the Diels-Alder reaction, locate the occupied and unoccupied orbitals associated with the DA reaction for both TSs by symmetry. Find the relevant MOs and add them to your wiki (at an appropriate angle to show symmetry). Construct a new MO diagram using these new orbitals, adjusting energy levels as necessary.
| LUMO of
Cyclohexadiene |
LUMO of
1,3-Dioxole |
||||||
|---|---|---|---|---|---|---|---|
| HOMO of
Cyclohexadiene |
HOMO of
1,3-Dioxole |
Figure 8: Jmols of the HOMOs and LUMOs of Cyclohexadiene and 1,3-Dioxole.
Endo
| MO40 (HOMO -1)
of Endo TS (A) |
MO41 (HOMO)
of Endo TS (S) |
||||||
|---|---|---|---|---|---|---|---|
| MO42 (LUMO)
of Endo TS (S) |
MO43 (LUMO +1)
of Endo TS (A) |
Figure 9: Jmols of the relevant Endo Transition State MOs.
Figure 10: MO Diagram for the formation of the Cyclohexadiene/1,3-Dioxole Endo TS. Note: This is an estimated MO diagram. The ordering of the MOs are accurate but the exact energy levels obtained from calculations done at the PM6 and B3LYP/6-31G(d) Levels were not used.
(It's quite difficult to see the phases in your TS MOs Tam10 (talk) 11:36, 30 October 2017 (UTC))
Exo
| MO40 (HOMO -1)
of Exo TS (A) |
MO41 (HOMO)
of Exo TS (S) |
||||||
|---|---|---|---|---|---|---|---|
| MO42 (LUMO)
of Exo TS (S) |
MO43 (LUMO +1)
of Exo TS (A) |
Figure 11: Jmols of the relevant Exo Transition State MOs.
Figure 12: MO Diagram for the formation of the Cyclohexadiene/1,3-Dioxole Exo TS. Note: This is an estimated MO diagram. The ordering of the MOs are accurate but the exact energy levels obtained from calculations done at the PM6 and B3LYP/6-31G(d) Levels were not used.
Questions
1. Is this a normal or inverse demand DA reaction? 6
As seen from the MO diagram, this is an Inverse Demand DA reaction. This is due to the (A-S-S-A) symmetry order of the Transition State MOs. 6
In a normal demand Diels-Alder reaction, the HOMO of the diene and the LUMO of the dienophile are more similar in energy (compared to the LUMO of the diene and the HOMO of the dienophile). This means that the strongest orbital interaction is between the most similar frontier molecular orbitals - HOMO of diene and LUMO of dienophile. In this case, the symmetry order of the Transition State MOs will be 'S-A-A-S' as illustrated in the MO diagram of Figure 13.
Figure 13: Expected MO diagram of a normal demand Diels-Alder reaction.
However, in an inverse demand Diels-Alder reaction, the LUMO of the diene and the HOMO of the dienophile are more similar in energy. This could be due to an electron-rich dienophile or an electron-poor diene. This means that the strongest orbital interaction is between the LUMO of the diene and the HOMO of the dienophile. As a result, the symmetry order of the Transition State MOs will be 'A-S-S-A', as illustrated in the MO diagram of Figure 12.
Hence, the Diels-Alder reaction between Cyclohexadiene and 1,3-Dioxole is an Inverse Demand one. This is not surprising as 1,3-Dioxole is an electron-rich dienophile (due to the oxygen atoms acting as electron-donating groups). The electron lone pairs in the p orbitals of the Oxygen atoms are able to delocalise into the π electron system of the C=C double bond, making the dienophile more electron rich.
Nf710 (talk) 00:21, 8 November 2017 (UTC) Excellent use of the MO diagram to show the ordering of the orbitals. This was presented very clearly was east to understand
2. Tabulate the energies and determine the reaction barriers and reaction energies (in kJ/mol) at room temperature
At the PM6 level,
| Compound | Sum of electronic and thermal Free Energies
(Hartrees / particle) |
Sum of electronic and thermal Free Energies
(kJ / mol) |
|---|---|---|
| Cyclohexadiene | 0.116874 | 306.85271 |
| 1.3-Dioxole | 0.052278 | 137.255899 |
| Endo TS | 0.137942 | 362.166749 |
| Endo Product | 0.037807 | 99.2622861 |
| Exo TS | 0.138902 | 364.687229 |
| Exo Product | 0.037977 | 99.7086211 |
Table 7: Summary of the 'Sum of electronic and thermal Free Energies' of the various reactants, transition states and products obtained at the PM6 Level.
| Endo Reaction Barrier
(kJ / mol) |
Endo Reaction Energy
(kJ / mol) |
Exo Reaction Barrier
(kJ / mol) |
Exo Reaction Energy
(kJ / mol) |
|---|---|---|---|
| 362.166749 - (306.85271+137.255899) = -81.94186 | 99.2622861 - (306.85271+137.255899) = -344.8463229 | 364.687229 - (306.85271+137.255899) = -79.42138 | 99.7086211 - (306.85271+137.255899) = -344.3999879 |
Table 8: Summary of the Endo/Exo reaction barriers and energies (in kJ/mol) obtained at the PM6 Level at room temperature
However, calculations done at the PM6 level are inaccurate as PM6 is a semi-empirical fitted method that uses experimental data to save time and resources during calculations. This can be seen from the negative reaction barrier values obtained for both the endo and exo cases. It is unlikely that the values of the reaction barriers are indeed negative, thus, calculations at the B3LYP/6-31G(d) level were done.
Also, instead of optimising the first point of the IRCs, reactants were taken at infinite separation to ensure fair comparison.
At the B3LYP/6-31G(d) level,
| Compound | Sum of electronic and thermal Free Energies
(Hartrees / particle) |
Sum of electronic and thermal Free Energies
(kJ / mol) |
|---|---|---|
| Cyclohexadiene | -233.324375 | -612593.193227 |
| 1.3-Dioxole | -267.068132 | -701187.43398 |
| Endo TS | -500.332150 | -1313622.1599 |
| Endo Product | -500.418691 | -1313849.3733 |
| Exo TS | -500.329165 | -1313614.3228 |
| Exo Product | -500.417321 | -1313845.7764 |
Table 9: Summary of the 'Sum of electronic and thermal Free Energies' of the various reactants, transition states and products obtained at the B3LYP/6-31G(d) Level.
| Endo Reaction Barrier
(kJ / mol) |
Endo Reaction Energy
(kJ / mol) |
Exo Reaction Barrier
(kJ / mol) |
Exo Reaction Energy
(kJ / mol) |
|---|---|---|---|
| (-1313622.1599) - ((-612593.193227)+(-701187.43398)) = 158.467307 | (-1313849.3733) - ((-612593.193227)+(-701187.43398)) = -68.746093 | (-1313614.3228) - ((-612593.193227)+(-701187.43398)) = 166.304407 | (-1313845.7764) - ((-612593.193227)+(-701187.43398)) = -65.149193 |
Table 10: Summary of the Endo/Exo reaction barriers and energies (in kJ/mol) obtained at the B3LYP/6-31G(d) Level at room temperature
3. Which are the kinetically and thermodynamically favourable products?
As seen from Table 10, the kinetically favourable product is the Endo product as it has the smaller reaction barrier.
The thermodynamically favourable product is also the Endo product as it has the more exothermic reaction energy.
Usually, the kinetically favourable product is the Endo product while the Thermodynamically favourable product is the Exo product.7 The Endo product is usually the kinetically favourable product due to favourable and stabilising orbital interactions, lowering the energy of the Endo transition state. The Exo product is usually the thermodynamically favourable product as it experiences less steric hindrance. Thus, it is the more (thermodynamically) stable product.
However, in this case, the Endo product is both the kinetically and thermodynamically favourable product. This could be due to factors such as secondary orbital interactions. The Endo product has stabilising secondary orbital interactions between the p-Orbitals of the Oxygen atoms and the back lobes of the diene, lowering the energy of the Endo product. Hence, the Endo product is (also) the thermodynamically favourable product (instead of the expected Exo product).
4. Look at the HOMO of the TSs. Are there any secondary orbital interactions or sterics that might affect the reaction barrier energy
| HOMO of Exo TS | HOMO of Endo TS | ||||
|---|---|---|---|---|---|
Figure 14: Jmols of the Exo and Endo Transition State HOMOs, showing secondary orbital interactions.
There are no significant secondary orbital interactions in the Exo Transition State. However, in the Endo Transition State, there is a stabilising secondary orbital interaction between the p-Orbitals of the Oxygen atoms (on the 1,3-Dioxole) and the LUMO of Cyclohexadiene. This stabilising interaction lowers the energy of the Endo Transition State, hence lowering the reaction barrier. Even though the Endo Transition State also experiences unfavourable steric interactions, this steric effect is minor and also helps in orientating the reactant FMOs for better overlap. Thus, the electronic factor dominates and this explains why the kinetically favourable product is the Endo Product.
Nf710 (talk) 00:26, 8 November 2017 (UTC) You have come to the correct conclusion. However Your arguments in steric are not quite correct and you can see this in the Jmols you have uploaded. Excellent script. You could have made it even better by including some info on the quantum methods that are used.
Exercise 3
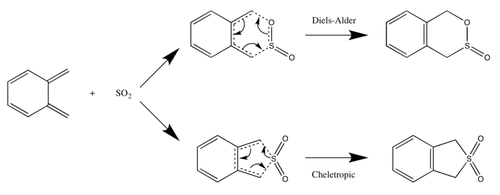
In this exercise, the Diels-Alder and Cheletropic reactions between o-Xylylene and SO2 were studied. For the Diels-Alder reactions, o-Xylylene acts as the diene while SO2 acts as the dienophile. The reactants, transition states and products were optimised at the PM6 level. IRC and frequency calculations were also done with the transition states.
Figure 15: Reaction scheme of o-Xylylene and SO2. Adapted from https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:ts_exercise#Exercise_3:_Diels-Alder_vs_Cheletropic
IRC Gifs
Visualise the reaction coordinate with an IRC calculation for each path. Include a .gif file in the wiki of these IRCs.
Figure 16: Animation Gif of the IRC of the Endo Product
Figure 17: Animation Gif of the IRC of the Exo Product
Figure 18: Animation Gif of the IRC of the Cheletropic Product
Calculations
Calculate the activation and reaction energies (converting to kJ/mol) for each step as in Exercise 2 to determine which route is preferred.
At the PM6 Level,
| Compound | Sum of electronic and thermal Free Energies
(Hartrees / particle) |
Sum of electronic and thermal Free Energies
(kJ / mol) |
|---|---|---|
| Xylylene | 0.178045 | 467.457183 |
| SO2 | -0.118614 | -311.421081 |
| Endo TS | 0.090562 | 237.770549 |
| Endo Product | 0.021702 | 56.9786053 |
| Exo TS | 0.092078 | 241.750807 |
| Exo Product | 0.021462 | 56.3484853 |
| Cheletropic TS | 0.099067 | 260.100428 |
| Cheletropic Product | 0.000002 | 0.0052510004 |
Table 11: Summary of the 'Sum of electronic and thermal Free Energies' of the various reactants, transition states and products obtained at the PM6 Level.
| Endo Reaction Barrier
(kJ / mol) |
Endo Reaction Energy
(kJ / mol) |
Exo Reaction Barrier
(kJ / mol) |
Exo Reaction Energy
(kJ / mol) |
Cheletropic Reaction Barrier
(kJ / mol) |
Cheletropic Reaction Energy
(kJ / mol) |
|---|---|---|---|---|---|
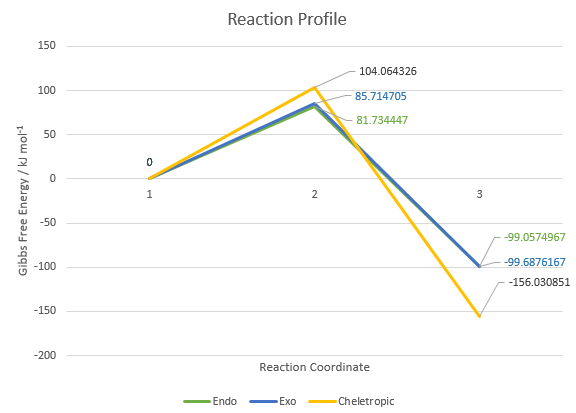
| 237.770549 - (467.457183 - 311.421081) = 81.734447 | 56.9786053 - (467.457183 - 311.421081) = -99.0574967 | 241.750807 - (467.457183 - 311.421081) = 85.714705 | 56.3484853 - (467.457183 - 311.421081) = -99.6876167 | 260.100428 - (467.457183 - 311.421081) = 104.064326 | 0.0052510004 - (467.457183 - 311.421081) = -156.0308509996 |
Table 12: Summary of the Endo/Exo/Cheletropic reaction barriers and energies (in kJ/mol) obtained at the PM6 Level at room temperature
The most kinetically favourable reaction would be the reaction with the smallest reaction barrier / lowest energy transition state. Therefore, as seen from Table 12, the most kinetically favourable reaction is the Endo Diels-Alder reaction, followed by the Exo Diels-Alder reaction and finally, the Cheletropic reaction.
The most thermodynamically favourable reaction would be the reaction with the most exothermic reaction energy / lowest energy product. Therefore, as seen from Table 12, the most thermodynamically favourable reaction is the Cheletropic reaction, followed by the Exo Diels-Alder reaction and finally, the Endo Diels-Alder reaction.
Reaction Profile
Draw a reaction profile that contains relative heights of the energy levels of the reactants, TSs and products from the endo- and exo- Diels-Alder reactions and the cheletropic reaction. You can set the 0 energy level to the reactants at infinite separation.
(Two many decimal places - these decimal places indicate trust in the precision of the calculation. When you subtract absolute energies, the results typically become very sensitive to geometry and even the architecture of the computer you're running on. Tam10 (talk) 11:42, 30 October 2017 (UTC))
Figure 19: Reaction Profile containing the relative heights of the energy levels of the reactants, TSs and products from the endo- and exo- Diels-Alder reactions and the Cheletropic Reaction. Reaction Coordinates 1, 2 and 3 refers to the reactants, TSs and products respectively.
As concluded from the previous section, it is expected that the Endo Diels-Alder reaction is the more kinetically favourable reaction while the Exo Diels-Alder reaction is the more thermodynamically favourable reaction.7 This is explained above in Exercise 2 Question 3 with stereoelectronic factors (i.e. steric hindrance and secondary orbital interactions).
Now considering the Cheletropic reaction, it is the most kinetically unfavourable reaction because of steric effects. For the Cheletropic reaction to occur, the diene has to adopt the cisoid conformation. Bulky groups/substituents tend to favour this cisoid conformation and hence, due to the lack of such bulky groups, the Cheletropic reaction is not kinetically favourable.8
The Cheletropic reaction is also the most thermodynamically favourable reaction because it results in a more stable five-membered ring product being formed. Sulfur is a relatively larger atom (than Carbon) and hence, a five-membered ring is more stable than a six-membered ring in this case.8
(Good additional analysis Tam10 (talk) 11:42, 30 October 2017 (UTC))
Questions
1. Xylylene is highly unstable. Look at the IRCs for the reactions - what happens to the bonding of the 6-membered ring during the course of the reaction?
Xylylene is highly unstable and reactive. This is because it has 2 cis-butadiene fragments. At each of the cis-butadiene fragments, xylylene can undergo reactions such as the Diels-Alder reaction. Furthermore, it is a planar molecule with 2 open faces, thus there are no significant steric hindrances either.
During the course of the reaction, the 6-membered ring becomes aromatic and the product becomes extremely stable. Each of the 6 C-C bonds are now equal in length, with a length value of 1.40 Å. This is an intermediate value between the average C-C (1.54 Å) and C=C (1.34 Å) bond length. This suggests that the 6 π electrons are delocalised over the planar ring system, hence making it aromatic according to Huckel's rule. The stability of the product drives the reaction forward, explaining the reactivity of Xylylene.
(A cyclic planar ring molecule is aromatic and follows Huckel's rule when the number of its π electrons equals to 4n + 2 where n = 0 or any positive integer.)
2. There is a second cis-butadiene fragment in o-xylylene that can undergo a Diels-Alder reaction. If you have time, prove that the endo and exo Diels-Alder reactions are very thermodynamically and kinetically unfavourable at this site.
| Compound | Sum of electronic and thermal Free Energies
(Hartrees / particle) |
Sum of electronic and thermal Free Energies
(kJ / mol) |
|---|---|---|
| Xylylene | 0.178045 | 467.457183 |
| SO2 | -0.118614 | -311.421081 |
| Endo TS | 0.102072 | 267.990056 |
| Endo Product | 0.065610 | 172.259068 |
| Exo TS | 0.105055 | 275.821924 |
| Exo Product | 0.067304 | 176.706665 |
Table 13: Summary of the 'Sum of electronic and thermal Free Energies' of the various reactants, transition states and products obtained at the PM6 Level.
| Endo Reaction Barrier
(kJ / mol) |
Endo Reaction Energy
(kJ / mol) |
Exo Reaction Barrier
(kJ / mol) |
Exo Reaction Energy
(kJ / mol) |
|---|---|---|---|
| 267.990056 - (467.457183 - 311.421081) = 111.953954 | 172.259068 - (467.457183 - 311.421081) = 16.222966 | 275.821924 - (467.457183 - 311.421081) = 119.785822 | 176.706665 - (467.457183 - 311.421081) = 20.670563 |
Table 14: Summary of the Endo/Exo reaction barriers and energies (in kJ/mol) obtained at the PM6 Level at room temperature
The Diels-Alder reactions at the second cis-butadiene fragment in o-xylylene are very thermodynamically and kinetically unfavourable.
Firstly, it is thermodynamically unfavourable due to the positive/endothermic reaction energies. As seen in Table 14, in both the endo and exo cases, the reaction energies are positive. On the other hand, the reaction energies of the Diels-Alder reactions at the first cis-butadiene fragment are negative/exothermic (Table 12) and hence more thermodynamically favourable.
Secondly, it is kinetically unfavourable due to the significant reaction barrier. Comparing the reaction barriers of the Diels-Alder reactions at the first and second cis-butadiene fragment (Table 12 and Table 14), the Endo reaction barrier has increased from +81.73 kJ/mol to +111.95 kJ/mol, while the Exo reaction barrier has increased from +85.71 kJ/mol to +119.79 kJ/mol. This suggests that Diels-Alder reactions at the second cis-butadiene fragment are more kinetically unfavourable.
Thus, Diels-Alder reactions at the second cis-butadiene fragment are more thermodynamically and kinetically unfavourable.
Conclusion
Several Diels-Alder reaction pathways were studied in the previous exercises. The way that the reactants approached each other had a significant impact on the transition state structure and product. For example, the amount of steric hindrance present depended on the approach of the reactants. Also, depending on the overlap of the reactants in the transition state, secondary orbital interactions may be present. Steric hindrances and secondary orbital interactions are examples of stereoelectronic factors that could affect the energies of the transition state/product and hence alter the predicted outcome of a reaction. An example can be found in Exercise 2, where the Endo product is (also) the thermodynamically favourable product due to stabilising secondary orbital interactions.
Log Files
For each of your calculations, upload the log file and include a link in the wiki
Exercise 1
| Compound/IRC | PM6 |
|---|---|
| Butadiene | File:Yrt13 BUTADIENE PM6 MO.LOG |
| Ethylene | File:Yrt13 ETHYLENE PM6 MO.LOG |
| Transition State | File:Yrt13 CYCLOHEXENE TS REOPT MO.LOG |
| Cyclohexene | File:Yrt13 CYCLOHEXENE PRODUCT REOPT PM6.LOG |
| IRC | File:Yrt13 IRC CYCLOHEXENE.LOG |
Table 15: List of log files obtained in Exercise 1.
Exercise 2
| Compound/IRC | PM6 | B3LYP/6-31G(d) |
|---|---|---|
| Cyclohexadiene | File:Yrt13 CYCLOHEXADIENE PM6 MO.LOG | File:Yrt13 CYCLOHEXADIENE 631Gd.log |
| 1,3-Dioxole | File:Yrt13 DIOXOLE PM6 MO.log | File:Yrt13 DIOXOLE 631Gd.log |
| Endo Transition State | File:Yrt13 E2ENDO TSPM6.LOG | File:Yrt13 E2ENDO TS631GD MO.LOG |
| Endo Product | File:Yrt13 E2 ENDO FINALPRODUCT.LOG | File:Yrt13 E2 ENDO FINALPRODUCT 631Gd.log |
| Endo IRC | File:Yrt13 IRC E2 ENDO PM6.LOG | |
| Exo Transition State | File:Yrt13 E2EXO TSPM6 MO.LOG | File:Yrt13 E2EXO TS631GD MO.LOG |
| Exo Product | File:Yrt13 E2 EXO FINALPRODUCT.LOG | File:Yrt13 E2 EXO FINALPRODUCT 631Gd.log |
| Exo IRC | File:Yrt13 IRC E2 EXO PM6.LOG |
Table 16: List of log files obtained in Exercise 2.
Exercise 3
| Compound/IRC | PM6 |
|---|---|
| Xylylene | File:Yrt13 E3 XYLYLENERXT2.LOG |
| SO2 | File:Yrt13 E3 SO2 MIN PM6.LOG |
| Endo Transition State | File:Yrt13 E3 ENDO TS PM6.LOG |
| Endo Product | File:Yrt13 E3 ENDOPRODUCTIRC PM6.LOG |
| Endo IRC | File:Yrt13 IRC Endo TS PM6.log |
| Exo Transition State | File:Yrt13 XYLYLENE TS.LOG |
| Exo Product | File:Yrt13 XYLYLENE FROZENREOPT2.LOG |
| Exo IRC | File:Yrt13 IRCXYLYLENE.LOG |
| Cheletropic Transition State | File:Yrt13 E3 CHELETROPIC TS PM6.LOG |
| Cheletropic Product | File:Yrt13 E3 Cheletropic2 PM6.log |
| Cheletropic IRC | File:Yrt13 IRC CHELETROPIC.log |
Table 17: List of log files obtained in Exercise 3.
Log files from the 'Extra' section regarding the second cis-butadiene fragment can be found here.
| Compound/IRC | PM6 |
|---|---|
| Endo Transition State | File:Yrt13 CISBUTADIENEENDOTS.LOG |
| Endo Product | File:Yrt13 ENDOPDTFROMIRC.LOG |
| Endo IRC | File:Yrt13 IRC cisbutadieneENDOTS.log |
| Exo Transition State | File:Yrt13 CISBUTADIENEEXOTS REOPT.LOG |
| Exo Product | File:Yrt13 EXOPDTFROMIRC.LOG |
| Exo IRC | File:Yrt13 IRC CISBUTADIENEEXOTS.LOG |
Table 18: List of log files obtained in Exercise 3 'Extra' section.
References
1. P. Deglmann and F. Furche, J. Chem. Phys., 2002, 117, 9535–9538.
2. R. M. Pitzer, J. Chem. Phys., 1973, 58, 3111.
3. S. S. Batsanov, Van der Waals Radii Elem., 2001, 37, 871–885.
4. A. G. Orpen, L. Brammer, F. H. Allen, O. Kennard, D. G. Watson and R. Taylor, J. Chem. Soc. Dalt. Trans., 1987, S1–S83.
5. K. N. Houk, J. GonzAlez and Y. Li, Acc. Chem. Res., 1995, 28, 81–90.
6. F. Liu, R. S. Paton, S. Kim, Y. Liang and K. N. Houk, J. Am. Chem. Soc., 2013, 135, 15642–15649.
7. J. H. Cooley and R. V. Williams, J. Chem. Educ., 1997, 74, 582–585.
8. D. Suárez, T. L. Sordo and J. A. Sordo, J. Org. Chem., 1995, 60, 2848–2852.