Rep:Yg5515ts

3rd Year Computational Lab---Transition states and Reactivity

In this Lab, the transition states (TS) of three Diels-Alder (DA) reactions were located and characterized by Gaussian.DA reactions play an important role in numerous new materials and natural products Method 3 was adopted to locate the transition state. The procedure started from the optimized structure of either the reactant or the product, then the lengths of bonds which were involved in the reaction were adjusted and freezed to resemble that of the transition structure. The guessed transition state was optimized and checked with frequency calculations and intrinsic reaction coordinate(IRC).

Introduction

Computational quantum chemistry has provided an efficient way to compute experimental complex and expensive experiments. Computational method is able to offer useful information of molecular geometries and properties, and reaction kinetics and energetic, and orbitals as well. In this lab, the reactivities of three DA reactions were explored by locating and characterizing the transition states from the PES. PES characterizes how the total potential energy varied as a function of the positions of nuclei geometry. Gaussian operates based on the Born-Oppenheimer approximation,which assumed that the nuclei are fixed in positions and electrons adjusts instantaneously to any movement of the nuclei. Gaussian investigates the electron distributions in accordance to the changes of nuclei geometries. For a molecule with N atoms, there are (3N-6) independent geometry variables which equal to the number of internal motions a molecule may have. ^[1]

Minimum energy point is the stationary point on the PES and it is defined by the zero value of the first derivative. At the stationary point, the change of potential energy with respect to all 3N-6 coordinates is zero.

$\frac{\partial E_{r}}{\partial r}$ = = -F(R) = 0

Figure 1 illustrates the reaction pathway from one energy minima to another via going through a transition state. The energy minima is a stationary point at which energy goes up in any directions on the PES, whereas transition state is a saddle point at which energy goes up in any directions apart from the coordinate aligned with the reaction pathway shown as the blue arrow in the figure

The "opt" in job type served as molecular geometry optimization in Gaussian, which can be applied to search the local minimum on the PES by employing mathematical algorithms.

Although the optimization can help us to find stationary point, but it cannot provide further information to identify whether the stationary point is a energy minima or a stationary saddle point. A stationary saddle point lies at the maximum for only one coordinate which is the reaction coordinate and all the others lie at the minimum.To distinguish whether the stationary point is a energy minima or a transition state,the curvature of the PES around the stationary point need to be determined and therefore frequency calculations are required. It can be done by explore the second derivatives, which is the force constant.

$\frac{\partial^{2} E_{r}}{\partial^{2} r}$ = = -F(R) = 0

The transition state is defined to satisfy the following relationship:

$\frac{\partial^{2} E_{r}}{\partial r^{2}}$ > 0 with one coordinate of $\frac{\partial^{2} E_{r}}{\partial r^{2}}$ < 0 This is manifested by the vibrational frequency analysis. There should be only one imaginary frequency for a transition state and zero for that of an energy minima.

The computational methods used in this lab were semi-empirical method PM6 and the Density Functional Theory (DFT) method B3LYP. PM6 was fast and relatively inaccurate compared with B3LYP. To carry out B3LYP, chemical species were optimized on PM6 level first.

Nf710 (talk) 09:07, 17 April 2018 (BST) You have shown a good understanding here. We actaully put the second derivatives that you have said above into a Hessian matrix. and diagonalisation gives all the force constants and the eigenvectors are the normal modes.

Exercise 1 Reaction of Butadiene with Ethylene

(Fv611 (talk) You are missing the discussion on the mechanism of bond formation, and are not showing the vibration corresponding to the bond forming mode. Additionally, your MO diagram is wrong: you are not at all taking into account the computed relative energies of your MOs.)

reaction scheme

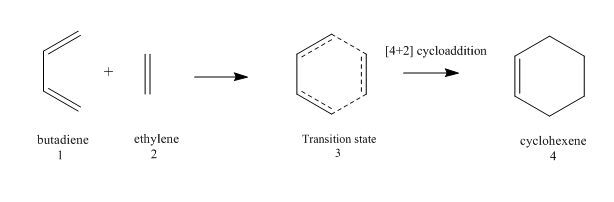
Current mechanism studies showed controversies in determining whether the reaction was proceeded via a one step concerted or a stepwise mechanism. In this exercise, the concerted TS was located by employing the method 3 with a frequency calculation. Reactants, the product and the transition state were all optimized by PM6.

Optimization at PM6 level

Table 1. Optimisation of Reactants, Product and transition state(PM6)

Butadiene

Ethlyene

transition state

Cyclohexene

Frequency calculation and IRC

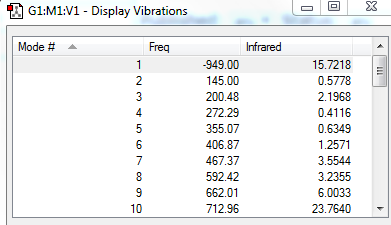
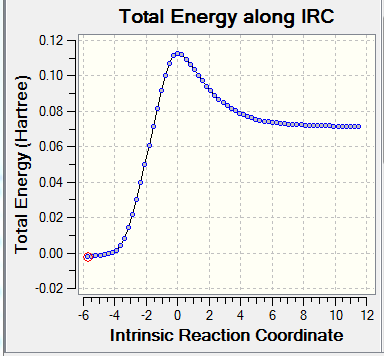
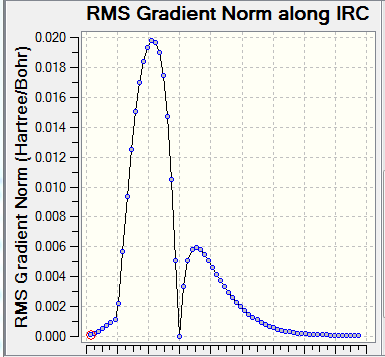
Table 2. Frequency calculation and IRC for TS
Frequency calculation	IRC(Total Energy)	IRC(RMS Gradient Norm)	reaction progress

The frequency calculation showed that the PM6 optimized transition state has one imaginary frequency at -949.cm^-1. An IRC analysis was done for confirmation. IRC followed a minimum energy pathway on the PES from the transition state to either the product or the reactant. In this experiment, an IRC path starting from the transition state to reactant was simulated. TS was successfully located and optimized because the energy gradients were at zero at the reactants , product and the TS.

MO analysis

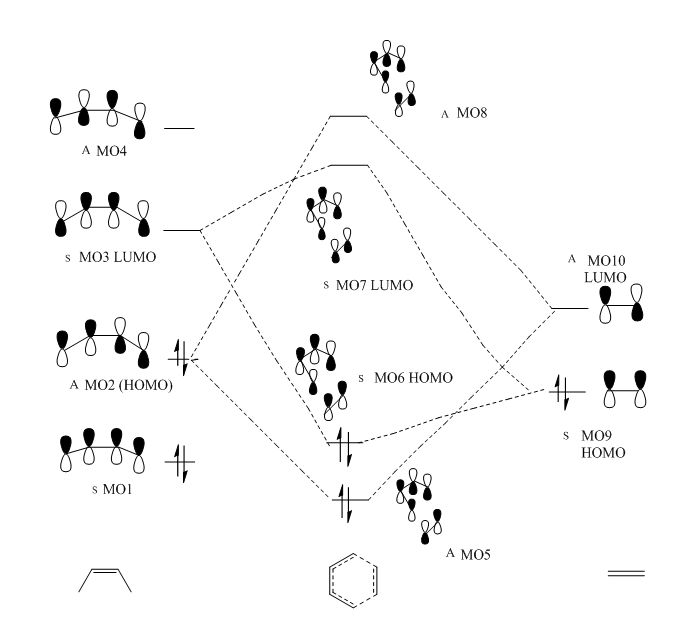
Figure 5, MO diagram of 1 reacting with 2. A represents asymmetric orbital label and S represents symmetric orbital label. HOMO is the highest occupied nolecular orbital and LUMO is the lowest occupied molecular orbital

Table 3. MO display of key orbitals (HOMO and LUMO)

Butadiene

Ethlyene

TS occupied orbitals (in phase interaction)

TS unoccupied orbitals (out of phase interaction)

A MO2(HOMO)

S MO9(HOMO)

S MO6(HOMO)

S MO7(LUMO)

S MO3 (LUMO)

A MO10 (LUMO)

A MO5

A MO8

Generally, molecular orbitals interact according to a set of rules.Firstly, only the MO which have the correct symmetry and close in energy tend to have large interactions. For example, the symmetric orbitals will interact with symmetric orbitals with non zero orbital overlap. This is also true for antisymmetric orbitals. However, orbital overlap is zero if symmetric orbital is combined with antisymmetric orbitals. In addition, HOMO and LUMO is a pair of occupied and unoccupied orbitals which closet in energy, therefore, the antisymmetric HOMO of butadiene (MO2) interacted strongly with the antisymmetric LUMO of enthylene, generating antisymmetric MO5 (bonding) and MO8 (antibonding). Also, the symmetric LUMO of butadiene (MO2) interacted strongly with the symmetric HOMO of enthylene, generating antisymmetric MO6 (bonding) and MO7 (antibonding). The occupied MO5 and MO6 of TS were resulted from in phase combination of the corresponding reactants' MO, whereas the occupied MO are generated by out of phase interactions.

Table 4. summary of orbital integrals
	antisymmetric orbital	symmetric orbital
antisymmetric orbital	non zero	zero
symmetric orbital	zero	non zero

The reaction is a [4+2] cycloaddition. Woodward-Hoffmann rule is the commonly applied to analyze the orbital symmetry requirement for DA reactions. In a thermal pericyclic reactions, the total number of (4q+2)s and (4r)a components need to be odd. s stands for suprafacial and a stands for antarafacial. As for suprafacial components, new bonds form on the same face at both ends, whereas an antarafacial component form new bonds at opposite faces.

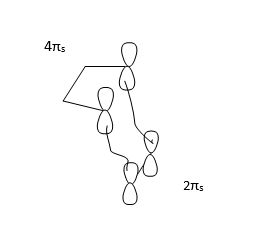
Figure 3 butadiene is a suprafacial component with four π electrons and the ethylene is also a suprafacial component with two π electrons

There is totally one component fit the (4q+2)s and (4r)a , therefore the reaction is allowed.

Carbon bond lengths

Keeping track of the changes of carbon bond lengths as the reaction progressed can provide useful information of the structure of the transition states , at which bonds are partially broken and formed. The hybridizations of the carbon atoms involved in the reaction have changed during the reaction. Therefore, the bond length also changed because it depended on the type of hybridization. The more s character the bond has, the stronger the electrons are hold to the nuclei thus the bond becomes shorter. sp2 hybridization has more s character than sp3 hybridization, so sp2-sp2 C-C is expected to be shorter than that of sp3-sp3 C-C. In addition, double bonds are shorter and stronger than single bonds, because the additional bonding attracted the nuclei stronger, pulling them closer.

Table 5. summary of carbon bond lengths
bond type	bond length/Å
sp3-sp3 C-C	1.54
sp2-sp2 C-C	1.47
sp2-sp3 C-C	1.5
sp2-sp2 C=C	1.34
vand der wal	1.7

Table 6. experimental bond length of reactants, product and transition state
Butadiene	Ethylene	transition state	cyclohexene

C1-C2:1.47 C1-C4:1.34 C2-C3:1.34	C1-C2:1.33	C1-C2:1.38 C2-C3:1.41 C3-C4:1.38 C5-C6:1.38 C1-C6:2.11 C4-C5:2.11	C1-C2:1.49 C1-C6:1.54 C6-C5:1.54 C4-C5:1.54

Table 7. explanation of bond lengths of the transition state
bond number	bond type changes	explanation
C1-C2/C3-C4	sp2-sp2 C=C to sp3-sp2 C-C	1.38 lies in the middle of the sp2-sp2 C=C (1.34) and sp3-sp2 C-C(1.5). The bond was lengthened to form a sp3-sp2 C-C bond
C2-C3	sp2-sp2 C-C to sp2-sp2 C=C	the bond was shortened to form a sp2-sp2 C=C
C1-C6	non-bonding to sp3-sp3 C-C	The sum of two carbon atoms' van der wal radii is 3.4Å, within which electrostatic attraction started to form, or in other words, a partial bond formed. The bond length is approximately the mean of the sum of two carbon atom's van der wal radii and the sp3-sp3 C-C.

Exercise 2 Reaction of Cyclohexadiene and 1,3-Dioxole

reaction scheme

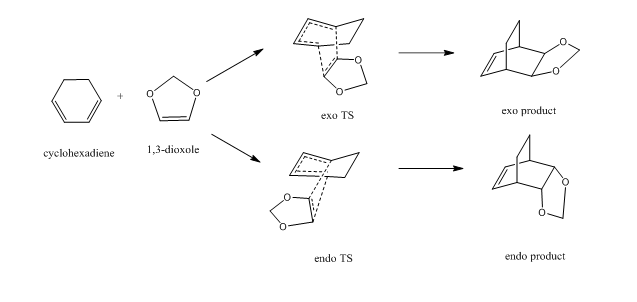
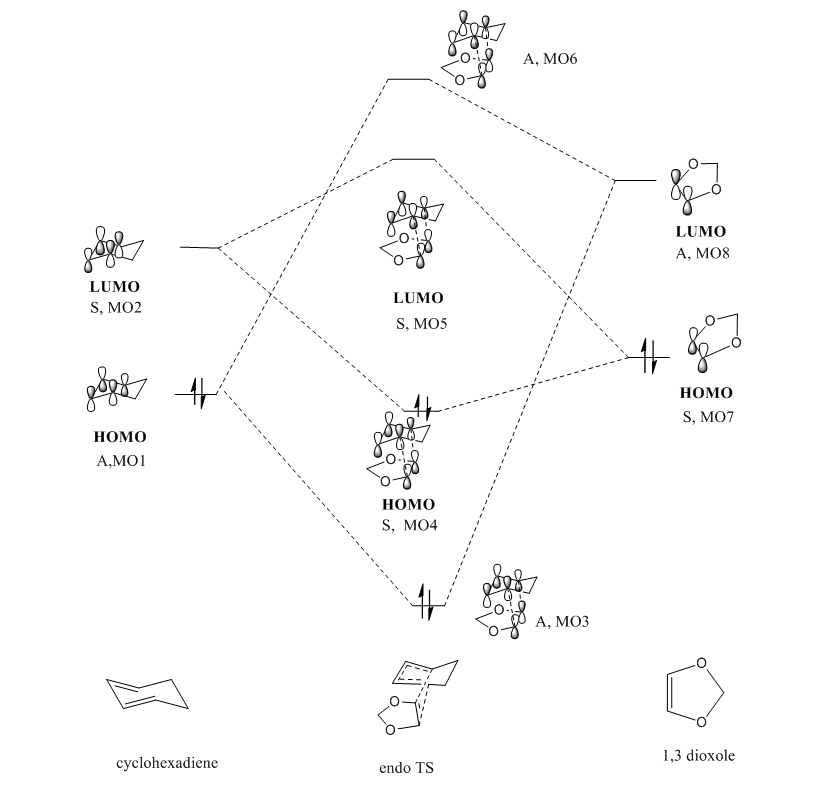
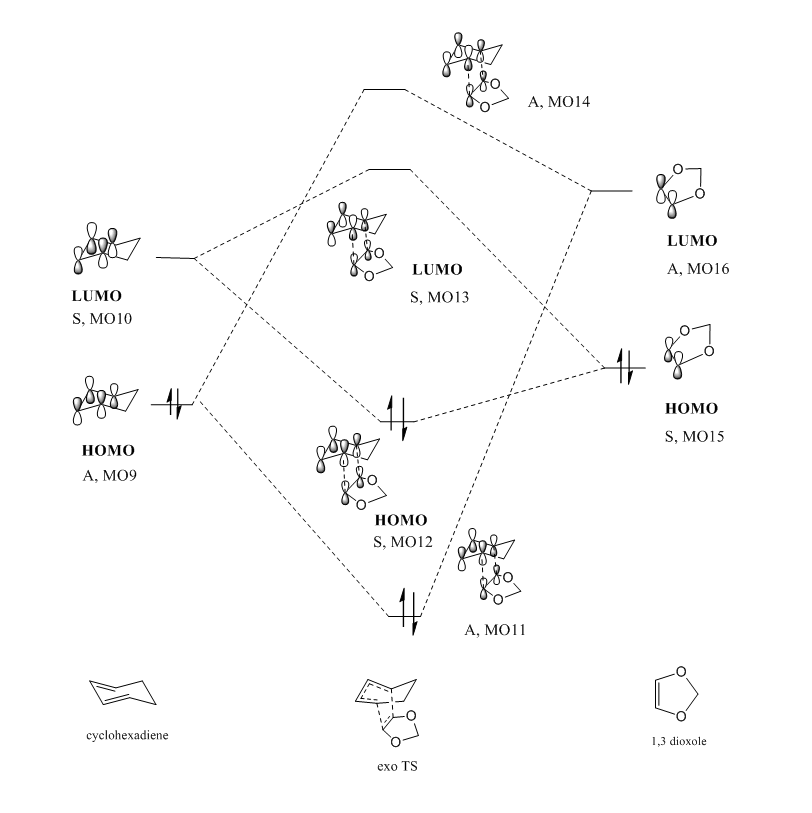
As shown in the reaction scheme, this DA reaction can proceed via two pathways ,leading to either endo or exo products depending on the orientation of 1,3-Dioxole in the TS. In this exercise, the reactants, products and both the endo and exo TS were optimized on a B3LYP/6-31G(d) level. A MO and thermochemical analysis were also conducted.

The TS were located and characterized by employing Method 3 in the Tutorial. Firstly, the product was optimized. The bonds which were involved in the reaction were broken, altered and freezed to make the structure resemble the TS. Then the coordinates were unfreezed and the TS were optimized by B3LYP/6-31G(d). All the structures were firstly optimized on a fast and rough PM6 level then optimized by the slow and more accurate B3LYP/6-31G(d) method.

Optimization of reactants and products

Table 8. B3LYP/6-31G(d) Optimisation of reactant and products

Cyclohexadiene

1,3-Dioxole

product(endo)

product (exo)

TS optimization and characterization

Table 9. B3LYP/6-31G(d)Optimisation of TS, frequency analysis and IRC

TS (endo)

TS (exo)

optimized structure

frequency analysis

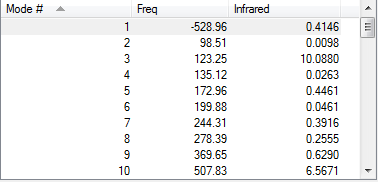
IRC(total energy)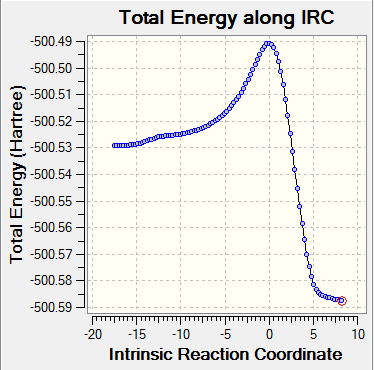

IRC( RMS gradient norm)

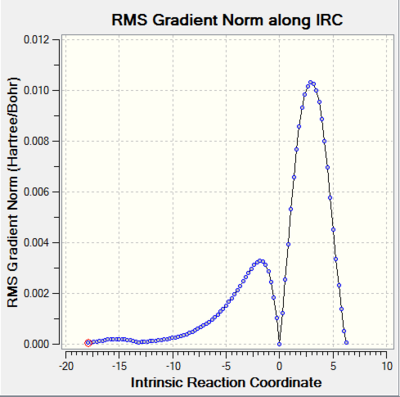
reaction progress

Both endo and exo TS have only one imaginary frequencies. The convergences in the log file were checked. The geometries of the optimized TS were consistent with the structures of their corresponding products. IRC analysis showed that the TS were successfully located because the energy gradients were zero.

MO analysis

(Fv611 (talk) As before, your MO diagrams are wrong.)

| |

Table 10. HOMO and LUMO of reactants, products and TS

Cyclohexadiene

1,3-Dioxole

TS(endo)

TS(exo)

HOMO

A, MO1

S, MO7

S, MO4

S,MO12

LUMO

S,MO2

A,MO8

S,MO5

S,MO13

Table 11.other key orbitals of TS

TS(endo)

TS(exo)

HOMO-1

A,MO3

A,MO11

LUMO+1

A, MO6

A, MO14

The MO interactions occurred in the region of HOMO and LUMO.

Table 12. energy comparison of endo and exo products and TS by B3LYP/6-31G(d))
chemical species	Sum of electronic and thermal Free Energiesy,Hartree	kJ mol^-1
Cyclohexadiene	-233.3243	-612593.14656
1,3-Dioxole	-267.0686	-701188.7195
TS(endo)	-500.3321	-1313622.0545
TS (exo)	-500.3291	-1313614.2305
product(endo)	-500.4186	-1313849.2732
product(exo)	-500.4173	-1313845.6730

The MO energies were checked with single point energies. It was observed that both the endo TS and endo product were more energetically stable than their exo counterpart. This is due to the extra stabilization resulted from the secondary orbital interactions.

Table 13. comparison of orbital interactions of the HOMO of endo and exo TS
TS endo	TS exo

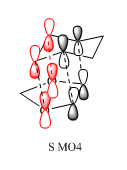
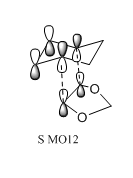
The reaction barriers were calculated as the energy differences between the total energy of reactants and the TS. Reaction energies, i.e. ΔG, was the energy differences between the reactants and products.

Table 14. Activation energy and ΔG for endo and exo reaction pathways
	Activation energy,kJ mol^-1	ΔG,kJ mol^-1
endo pathway	159	-68
exo pathway	167	-64

The four red p orbitals indicated in the diagram are involved in the secondary orbital interaction. There are significant interactions between the non bonding orbitals of the oxygen atoms and the p orbitals of the diene component.The four p orbitals combined in phase. As the endo transition state was stabilized, the energy barrier for endo pathway was expected to be smaller than that of the exo pathway. Therefore, the activation energy of endo pathway was lower and ΔG was more negative. Overall, in combination of the single energy analysis, the endo products are both the kinetically stable and thermaldynamically stable products.

Normal or Inverse electron demand

According to the energy differences between the LUMO and HOMO pairs of the reactants and products, DA reactions are classified as two types: Normal electron demand: electron deficient dienophile with low energy LUMO and the electron rich diene with high energy HOMO Inverse electron demand: electron rich dienophile with high energy LUMO and the electron difficient diene with low energy HOMO

Table 15 Energy difference of different LUMO and HOMO pairs
	HOMO energy/a.u.	LUMO energy/a.u
Cyclohexadiene	-0.20554	-0.01711
1,3-Dioxole	-0.19594	+0.03795

ΔE of HOMO (Cyclohexadiene) and LUMO (1,3-Dioxole):0.243 ΔE of HOMO (1,3-Dioxole) and LUMO (Cyclohexadiene):0.179

The closer the energies of two molecular orbitals, the larger the interactions. The energy difference between the HOMO of cyclohexadiene and LUMO of 1,3-Dioxole, therefore, this DA reaction has an inverse electron demand. 1,3-Dioxole has high energy LUMO because the lone pairs of the two oxygen atoms have the ability to donate electrons into the π cloud, raising the orbital energies.

Nf710 (talk) 09:18, 17 April 2018 (BST) Your analysis of the MOs was good. and you have correctly deduced the electron demand of the reaction. well done. Your energies were correct and there for you have come to correct conclusions. This was your best section.

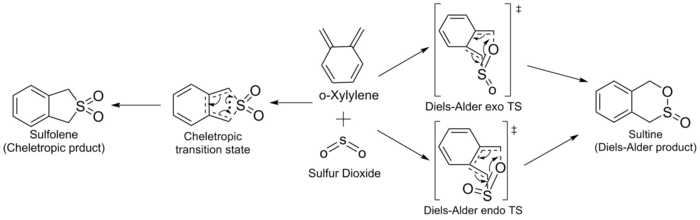
Exercise 3 o-Xylylene-SO2 Cycloaddition

reaction scheme

The reaction of o-Xylylene and SO2 can proceed via two pathways, DA and cheletropic. The DA reactions can go through both endo and exo transition state to the sultine product. The TS is a six membered heteroaromatic ring with 6 π electrons involved. The cheletropic reaction is a separate class of pericyclic reactions, they must also obey the Woodward Hoffmann rules. According to the selection rules for cheletropic reactions, o-Xylylene and SO2 reacted through a disrotatary fashion which the HOMO of the S atom pointed directly to the π system of the o-Xylylene, because the π system has 4n+2 π electrons. The TS is a five membered heteroaromatic ring with also 6 π electrons.^[2]

PM6 optimization

The reactants, products and TS were optimized on PM6 level and the TS s were located by Method 3. Products were firstly optimized. Then, the bonds involved in the reaction were broken ,frozen and optimized to obtain a guessed TS stucture. The coordinated were unfrozed and optimized again to obtain the accurate TS structure.

Table 16 PM6 optimization of reactants

o-Xylylene

SO2

Table 17 PM6 optimization of endo and exo products and TS

products

TS

endo

exo

Cheletropic

(Your cheletropic TS and product geometries are wrong. The oxygen atoms are too close together and have bonded. Your exo geometries are actually endo Tam10 (talk) 15:11, 4 April 2018 (BST))

TS characterization

IRC and frequency analysis were carried out to confirm a TS has been successfully located. All the IRC showed that the energy gradients were zero at reactants, transition states and products. All the reactions were proceeded via a concerted fashion. It was observed that the energies involved in the reaction were quite small compared with the reactions in exercise 1 and exercise 2 which was due to the high energy o-Xylylene. For both the endo and exo DA pathways, two single bonds were formed, i.e. C-S and C-O, meanwhile, two C=C were reduced to one C=C as well as the S=O. In cheletropic pathway, two C-S were formed and two C=C were reduced to one.^[3]

Table 18 TS characterization of endo and exo pathways at PM6 level
	reaction progress	IRC(total energy)	IRC(energy norm gradient)
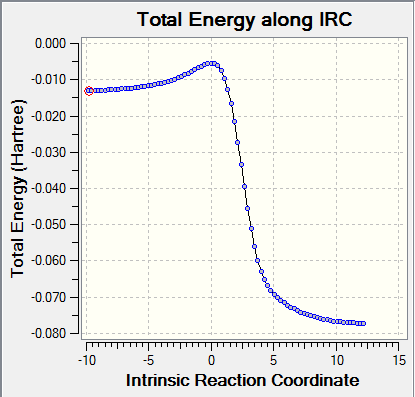
endo
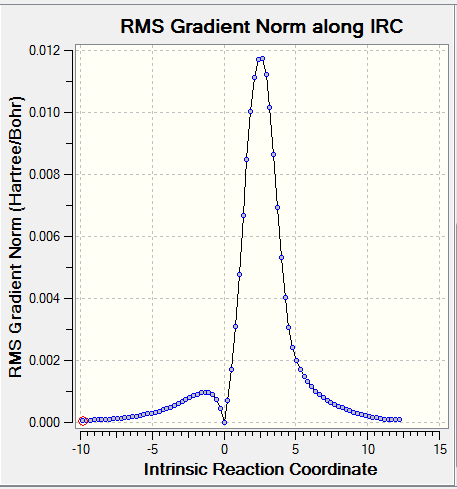
exo
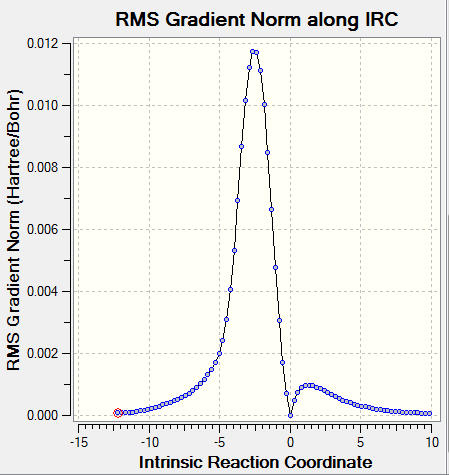
Cheletropic

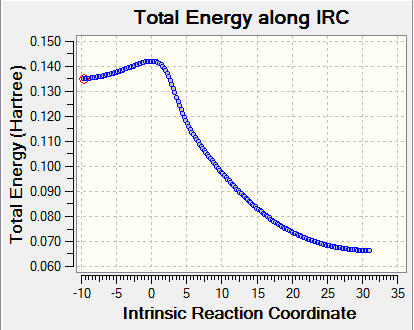
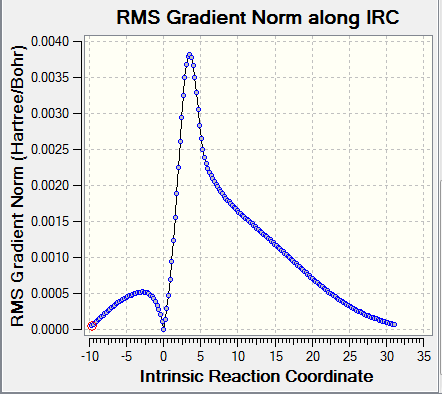
For all the chemical species, convergences were checked. As for the reactants and products, there were no imaginary frequencies present and for TS, there was only one imaginary frequency.

Thermochemical analysis

The energies of reactants, products and TS were obtained from the log files. Activation barriers and ΔG were calculated.

Table 19. energy comparison of endo and exo products and TS by B3LYP/6-31G(d))
chemical species	Sum of Electronic and Thermal Free Energies/Hartree	kJ mol^-1
o-Xylylene	+0.179059	+470.119
SO₂	-0.119268	-313.496
Diels-Alder Exo TS	+0.090559	+240.286
Diels-Alder Endo TS	+0.090559	+237.762
Cheletropic TS	+0.099377	+260.914
Diels-Alder Exo Product	+0.021700	+56.973
Diels-Alder Endo Product	+0.021696	+56.963
Cheletropic Product	+0.000006	+0.0158

(Your cheletropic energy is inconsistent with the Jmol and log file you've produced Tam10 (talk) 15:11, 4 April 2018 (BST))

Table 20. Activation energies and reaction energies
	Activation energy,kJ mol^-1	ΔG,kJ mol^-1
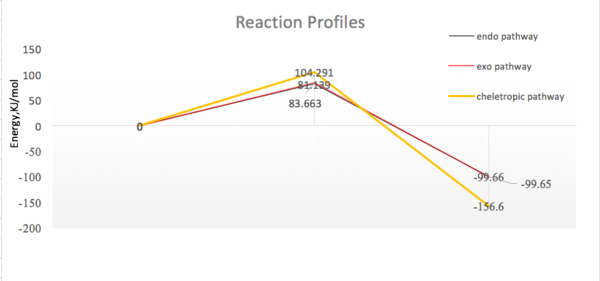
endo pathway	81.139	99.66
exo pathway	83.663	99.65
cheletropic reaction	104.291	156.60

Activation barriers were calculated by the differences between the sum of energies of two reactants and the TS. ΔG was obtained by calculating the differences between the free energies of reactants and products.

reaction profile

It was assumed that the reactants have zero energies with infinite separations. The reaction profile showed relative height of the TS and products of the three reaction pathways. Cheletropic products were the thermodynamic products because they were most energetically stable. There were extremely small energy differences between the exo and endo transition states as well as the products. However, the endo products and TS were slightly more stable than that of the exo. Therefore, the kinetic and thermodynamic products were generated from the endo pathway.Apart from the steric interactions, favorouble orbital interactions also play a role in energy stabilization. The non bonding p orbitals of S=O interacts with the π system.

Files: Ex1:

butadiene : File:Yihan butadiene.LOG

transition state: File:Yihan TS PM6.LOG

cyclohexene: File:Yihan cyclohexene.LOG

Ex2

Cyclohexadiene: File:Yihan reactant 1.LOG

1,3-Dioxole : File:YihanREACANT 2 OPT.LOG

endo product:File:YihanPRODUCT ENDO OPT.LOG

exo product : File:YihanPRODUCT EXO OPTIMIZED.LOG

Ex3

o-Xylylene: File:Yihan o-Xylylene.LOG

SO2: File:Yihan REACTANT SO2.LOG

Endo TS: File:Yihan ex3 ENDO TS UNFREEZ.LOG

Exo TS: File:Yihan ex3EXO TS3.LOG

Cheletropic product: File:Yihan chele PRODUCT.LOG

Cheletropic TS: File:Yihan chele TS.LOG

Exo product: File:YihanEXOPRODUCT PM6.LOG

Endo product: File:Ex3ENDO PRODUCT.LOG

References

↑ Ot, W. J. (1990). Computational quantum chemistry. Journal of Molecular Structure: THEOCHEM (Vol. 207).
↑ Woodward, R.B.; Hoffman, R. Angew. Chem. Int. Ed. Engl. 1969, 8, 781–853.
↑ Woodward, R.B.; Hoffman, R. Angew. Chem. Int. Ed. Engl. 1969, 8, 781–853.

[1] Ot, W. J. (1990). Computational quantum chemistry. Journal of Molecular Structure: THEOCHEM (Vol. 207).

[2] Woodward, R.B.; Hoffman, R. Angew. Chem. Int. Ed. Engl. 1969, 8, 781–853.

[3] Woodward, R.B.; Hoffman, R. Angew. Chem. Int. Ed. Engl. 1969, 8, 781–853.

[1]

[2]

[3]