Rep:Yc9014-transition

Introduction

Exercise 1:Reaction of Butadiene with Ethylene

molecular orbital structure

HOMO and LUMO of both reactants can be visualized by GaussiView and shown in table 1 as following.

Table1. HOMO and LUMO of reagents butadiene and ethene
	HOMO	LUMO
cis-Butadiene
	Anti-symmetric (AS)	Symmetric (S)
Ethylene
	Symmetric (S)	Anti-symmetric (AS)

After the transition state was optimized and its identity proved by IRC, graph of the energy levels proceed from HOMO and LUMO of the reactants was visualized and shown in table 2.

Table 2. energy levels for transition states of the reaction of butadiene and ethylene
HOMO-1	HOMO	LUMO	LUMO+1

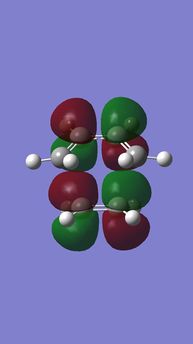
Anti-symmetric (AS)	Symmetric (S)	Symmetric (S)	Anti-symmetric (AS)

From the graphs in table 2

HOMO-1 is a in-phase combination of butadiene HOMO(AS) and ethylene LUMO(AS),

HOMO is a in-phase combination of butadiene LUMO(S) and ethylene HOMO(S),

LUMO is a anti-phase combination of butadiene LUMO(S) and ethylene HOMOMO(S),

LUMO+1 is a anti-phase combination of butadiene HOMO(AS) and ethylene LUMO(AS)

MO daigram

With these combination relationship and relative energy levels above, a MO diagram can be drawn as graph 1.

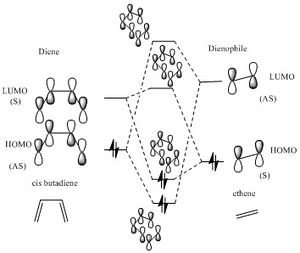
Graph 1. MO diagram of transition state for reaction of butadiene and ethylene.

(Fv611 (talk) 16:06, 5 April 2017 (BST) MO diagram is correct but very hard to read do to its scale. Additionally you didn't label the TS MOs.)

As indicated from graph 1,the symmetry of two potential reacting orbitals must match with each other. ie. symmetric orbital interacts with symmetric orbitals, asymmetric orbital interacts with asymmetric orbitals. The orbital overlap can only be none-zero when the two orbitals have the same symmetry.The relationship of symmetry interaction and orbital overlap shown in table 3. For symmetrically mismatched orbitals(symmetric with asymmetric), no overlap means no interaction, therefore, no reaction happen.

table 3
symmetry interaction	Orbital overlap integral
AS-AS	None-zero
AS-S	zero
S-S	none-zero

bond length

table 4 typical bond length
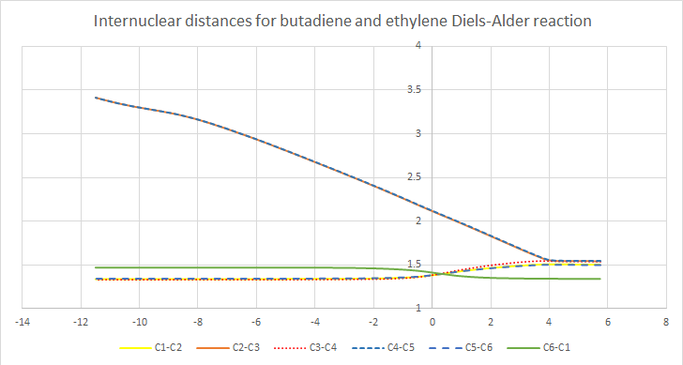
bond	bond length(Å)
sp3-sp3	1.54
sp3–sp2	1.50
sp2–sp2	1.47
benzene	1.40
alkene	1.34

As can see from graph 2 , the bond length of the double bond in butadiene and ethylene decreases and the single bond in butadiene experiences a increase in bond length while two new bonds forms between two molecules. The Van der Waals radius of the C atom is 1.70. the partly form C-C bond has a bond length(2.14 Å) longer than normal sp3-sp3 single bond(1.54 Å).

(Fv611 (talk) 16:06, 5 April 2017 (BST) Even though you did compute the bond lenghts, you didn't report which length corresponds to which bond in your Figure 3. This led you to failing to appreciate that the bond lenght of the C2-C3 and C4-C5 bonds at the transition state is at an intermediate value between sp3 bonding length and 2 x the Van der Waals radius of Carbon atoms.)

reaction path at the transition state

Both reactants and the transition state are symmetric, two bonds are identical and form synchronously.

Exercise 2:Reaction of Cyclohexadiene and 1,3-Dioxole

Molecular orbitals

Following molecules are optimised at PM6 level. Cailulation of transition state at B3LYP/6-31G(d) level was conducted but failed due to unsolved software reason. Transition state of endo producted was reached and proved by IRC .Transition state of exo product met a "Maximum number of corrector steps exceeded" issue. Although additional keyword 'IRC=MaxCycle=n' was used, the IRC calculation still failed. If more time was given, this problem can be potentially fixed by setting the 'correction steps' to 'never and optimising again. MO graph shown as follow. HOMO and LUMO for reactants table 5.HOMO and LUMO for endo transition state table 6 and exo transition state table 7.

(What was the software issue? Was it raised with one of the demonstrators? Tam10 (talk) 18:21, 3 April 2017 (BST))

Table5. HOMO and LUMO of reagents butadiene and ethene
	HOMO	LUMO
cyclohexdiene
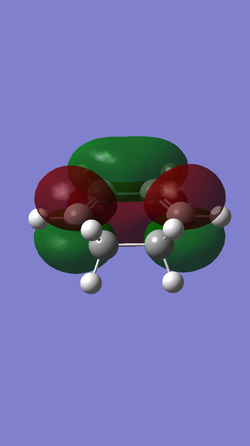
	Anti-symmetric (AS)	Symmetric (S)
dioxole
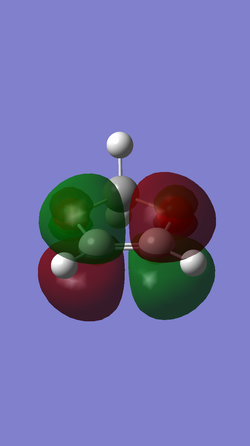
	Symmetric (S)	Anti-symmetric (AS)

Table 6. energy levels for transition states of endo DA reaction of Cyclohexadiene and 1,3-Dioxole
HOMO-1	HOMO	LUMO	LUMO+1

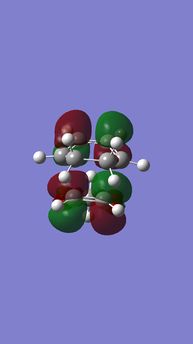
Anti-symmetric (AS)	Symmetric (S)	Symmetric (S)	Anti-symmetric (AS)

Table 7. energy levels for transition states of the exo DA reaction of Cyclohexadiene and 1,3-Dioxole
HOMO-1	HOMO	LUMO	LUMO+1

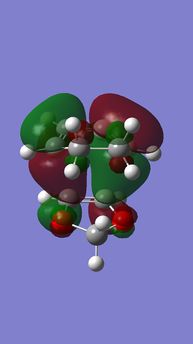
Anti-symmetric (AS)	Symmetric (S)	Anti-ymmetric (AS)	Symmetric (S)

It can been seen from the graph 6 that endo product has the same orbital symmetry order (AS/S/S/AS from LUMO-1 to HOMO +1) with the the cyclohexene formation in exercise one, so it has a similar MO diagram with as graph**. However, the exo transition state has a different orbital symmetry order(AS /S/AS/S from LUMO-1 to HOMO) table 7. So the MO diagram is adjusted as following graphs.

It is an inverse DA reactions. A normal DA reaction happen between a electron-poor dienophile and an electron rich diene. An inverse DA happen between an electron-rich dienophile and an electron-poor diene. In the case, the diene is not very electron poor nor electron rich, but dienophile 1,3-Dioxole is very electron rich due to direct attach to two electron donating oxygen atom. The orbital energy rises in dienophile and HOMO of dienolphile interact with LUMO of diene and form most energetically favored new orbital

Energy barrier and reaction energy

At room temperature,1 Hartree= 627.509 kcal mol-1

(Why are you using kcal/mol? Below you write kJ/mol when they are kcal/mol values Tam10 (talk) 18:21, 3 April 2017 (BST))

energy for Cyclohexadiene,0.118067. energy for 1,3-Dioxole -0.052286. Energy for reatant=(0.118067-0.052286) $\times$ 627.509kcal mol-1=41.27 kJ mol-1

energy for endo transition state, 0.137943 $\times$ 627.509kcal mol-1=86.56 kJ mol-1 energy for endo product,0.037803 $\times$ 627.509kcal mol-1=23.72 kJ mol-1

energy for exo transition state, 0.138903 $\times$ 627.509kcal mol-1=87.16 kJ mol-1 energy for exo product,0.037975 $\times$ 627.509kcal mol-1=23.83 kJ mol-1

table 8. Activation energy and reaction energy for each route
	activation energy	reaction energy
exo	45.89	$- 17.44$
endo	45.29	$- 17.55$

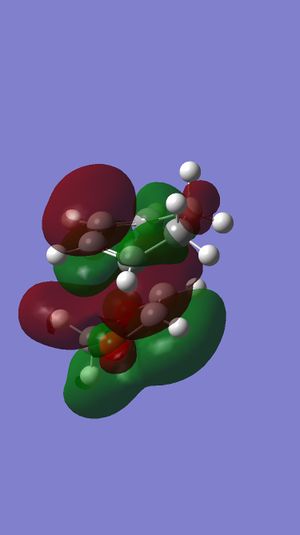
The calculation shows that endo product are both kinetic and thermo product. Endo product is the kinetic product because of the secondary effect. as can be seen from the graph below, the two middle orbitals on diene LUMO has a favorable interaction with the orbital from oxygen, which lower the energy of the transition state and facilitates the endo reaction.

Nf710 (talk) 13:54, 16 April 2017 (BST) You have got the correct conculsion and you have explained the SOO. However you should have used b3LYP and told the demonstators that your Guassian was not working as this could have been fixed.

Exercise 3:Diels-Alder vs Cheletropic

reaction coordinate with IRC calculation

Table 9. reaction coordinate for three routes
cheletropic product	endo	exo

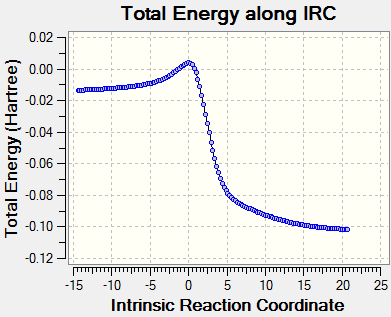
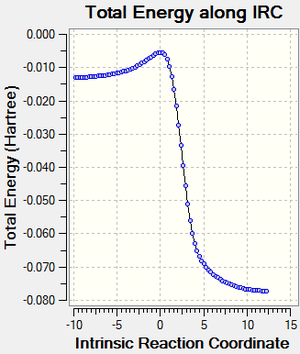
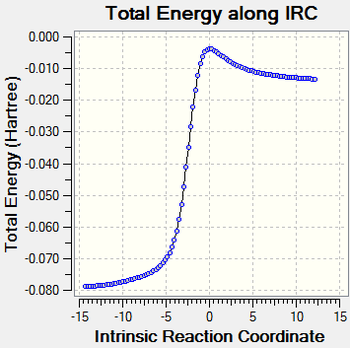
NOTE: the exo TS is optimized in a different route so its IRC are from the product to reactants.The reactants to product graph is its inverse version from y axis.

Table 10. IRC path for three routes
cheletropic product	endo	exo

Activation energy and reaction energy

At room temperature

The energy measurement in GaussView is in Hartree, 1 Hartree= 627.509 kcal mol-1

energy for so2, -0.118614.energy for xylyene,0.178554. Energy of the reactants=(-0.118614+0.178554) $\times$ 627.509kcal mol-1=37.61 kJ mol-1

energy for exo 6-membered-ring TS, 0.092079 $\times$ 627.509kcal mol-1=57.78 kJ mol-1

energy for exo 6-membered-ring product, 0.056109 $\times$ 627.509kcal mol-1=35.21 kJ mol-1

energy for endo 6-membered-ring TS, 0.090559 $\times$ 627.509kcal mol-1=56.83 kJ mol-1

energy for endo 6-memberd-ring product, 0.021700 $\times$ 627.509kcal mol-1=13 kJ mol-1

energy for 5-memberd-ring TS, 0.099060 $\times$ 627.509kcal mol-1=62.16 kJ mol-1

energy for 5-memberd-ring product, -0.000002 $\times$ 627.509kcal mol-1=-0.0012 kJ mol-1

Table 11. Activation energy and reaction energy for each route
	activation energy	reaction energy
exo 6-membered-ring	20.17	$- 2.4$
endo 6-membered-ring	19.22	$- 24.61$
5-memberd-ring	24.55	$- 37.61$

(exo reaction energy should be more exothermic Tam10 (talk) 18:21, 3 April 2017 (BST))

The endo Diels-Alder product is kinetically preferred as it has lowest activation energy. The cheletropic product is aerodynamically preferred as it has lowest reaction energy.

(Check your work for autocorrections and typos like this! Tam10 (talk) 18:21, 3 April 2017 (BST))

Draw the reaction profile for all three routes in one graph (graph 7).

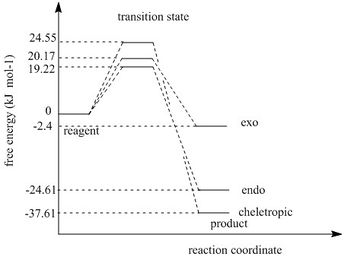
As can be seen in the graph. cheletropic product has the lowest energy so it is thermodynamic product. Endo product is the kinetic product.

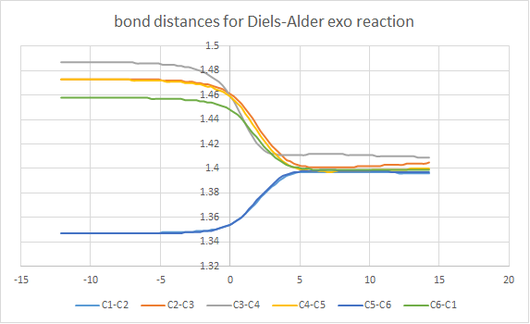
bond length of the 6-membered ring in xylyene

(This is a nice use of the Python code. You should probably show explicitly which bonds these are, but it's clear that there is some aromaticity being developed in this just after the TS Tam10 (talk) 18:21, 3 April 2017 (BST))

As can be seen from the graph, all nbond lengths changed. Two double bond on the ring extends and sing bonds shortens and finally all of they reaches a similar distances as the electron density delocalise in the 6 membered ring. The graph of endo and exo product are similar as they share the same structure. Cheletropic product has one bond slightly long than other. This is because the bond is shared with the neighboring 5 membered ring and experience a additional ring strain.

Conclusion

In this computational lab, transition states of three Diels-Alder reactions are constructed and analysed by GaussView. For a Diels-Alder reaction starts from a substituted dienophile, the endo route is preferred because of the additional secondary interaction which lowers the activation energy. Exercise 1 and Exercise 2 researches the molecular orbital interaction and formation of HOMO and LUMO for the products. Exercise 2 and Exercise 3 focus on the relative energy barrier and reaction energy for different reaction routes and determine the kinetic and thermo product with the aid of these energies.

GaussiView is used to optimise the molecules and visualise the molecular orbitals. In this experiment, PM6 is most commonly used to achieve a reasonable optimization for small molecule. B3LYP/6-31G(d) level calculation is more time consuming but will give a more accurate result.