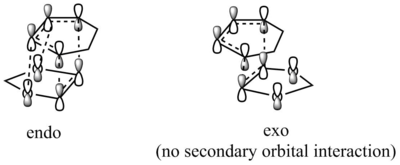Introduction

Transition State

To investigate a reaction, it is crucial to firstly locate the Transition State of the reaction. The transition state of a reaction, on a 2D reaction coordinate, will be the highest point of energy connecting reactants and the products. In addition, it should also have the characteristics as shown below:

$\frac{\partial V}{\partial q_{i}}$ = 0

$\frac{\partial^{2} V}{\partial q_{i}^{2}}$ < 0

Where as being a stationary point, its first derivative is equal to 0, while its second derivative should be negative as being the highest point on the reaction profile.

On a 3D PES (Potential Energy Surface), it is more difficult to determine the transition state, as it will be one saddle point among many other existing saddle points, however, being the maximum point on the minimum energy path, its first derivative and second derivative will both be equal to zero.

$\frac{\partial V}{\partial q_{i}}$ = 0

$\frac{\partial^{2} V}{\partial q_{i}^{2}}$ = 0

Nf710 (talk) 11:35, 7 March 2018 (UTC) Guassian works on a 3N-6 Potential energy surface. You get the force constants by diagonalising the Hessian matrix

Computational Methods

In this report, three different pericylic reactions were investigated using computational methods, including the PM6 and the B3LYP/6-31G(d) Methods.

PM6, with its full name being Parameterization Method 6, is a semi-empirical method. This method is based on the Hartree-Fock Model, and the model works by minimising the total molecular potential energy by varying the expansion coefficients, c_μi, which is the coefficient in the equation of LCAO (Linear Combination of Atomic Orbitals).

This method is not perfect as it is based on the wrong assumption of accounting electrons as being largely independent of each other.^[1]

Nf710 (talk) 11:39, 7 March 2018 (UTC) What you mean is that PM6 ignores the 2 electron integrals

In reality, this is not true and the electrons will repulse each other due to their negative charge. Therefore, this method needs to be parameterised, which means the results fitted by a set of parameters, to product results that agree the most with experimental data.

While the other method, B3LYP, representing Becke, three-parameter, Lee-Yang-Parr, is based on Density Fucntional Theory (DFT), which is an incorporation of partly exact exchange from Hartree–Fock theory as well as exchange-correlation energy from other sources. It has an exchange-correlation functional as shown below:

$E_{x c}^{B 3 L Y P} = E_{x}^{L D A} + a_{0} (E_{x}^{H F} - E_{x}^{L D A}) + a_{x} (E_{x}^{G G A} - E_{x}^{L D A}) + E_{c}^{L D A} + a_{c} (E_{c}^{G G A} - E_{c}^{L D A}),$

where $a_{0} = 0.20$ , $a_{x} = 0.72$ , and $a_{c} = 0.81$ . ^[2]^[3]

6-31G is a basis set of basis function among many others including 3-21G, etc.

Nf710 (talk) 11:39, 7 March 2018 (UTC) Well done. You have clearly red beyonf the script here and included the equations. Good work.

Optimisation Methods

In this lab, three methods were used to optimise the TSs, with difficulty increasing from Method 1 to Method 3. Method 1 is the easiest and fastest one, but it is based on existing knowledge of the Transition State. Method 2, compared with Method 1, is more reliable as well as relatively fast, but it also has the limitation of requirement on knowledge of TS. Method 3 takes the most time to run, however, it does not have the limitation of the first two methods.

In this report, three pericylic reactions were investigated with all the Transition States being run with Method 3 and will be shown below.

Excercise 1- Diels-Alder reaction of butadiene with ethylene

(Fv611 (talk) Good job on the whole exercise. Well done!)

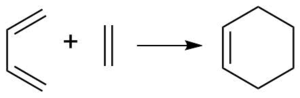
This reaction is a classical [4+2] cycloaddition (Diels-Alder) reaction. In this reaction, cis-butadiene reacts with ethylene to form cyclohexene with complete regioselectivity because there are no substituents attached to the reactants.

In Excercise 1, this reaction was investigated and analysed by optimising the reactants, products, and the Transition State to a minimum using PM6 Method in GaussView 5.0.9 software. In addition, their MOs and vibration frequencies, as well as the IRC (Intrinsic Reaction Coordinate) were obtained and analysed.

Optimisation

Optimisation of reactants and products at PM6 level

Table 1. Optimisation of reactants and products
Optimisation of Reactants and Product
Reactant: Butadiene	Reactant: Ethlyene	Product: Cyclohexene

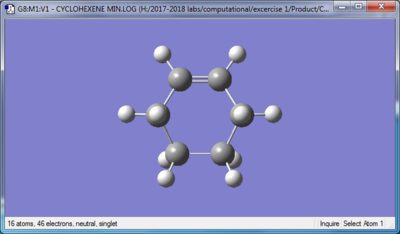
Optimisation of transition state at PM6 level

Table 2. Optimisation of TS
Optimisation of Transition State
Transition state

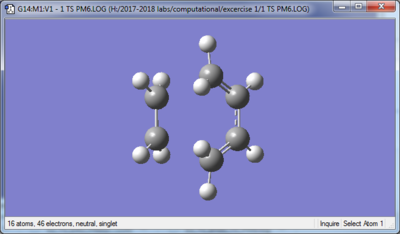
Confirmation of correst TS using frequency calculation and IRC

Table 3. IRC of the transition state
Frequency calculations and IRC
Vibration frequencies of the TS	IRCs
Figure 1(a) Vibration frequencies of the TS	Figure 1(b) Total energy along IRC Figure 1(c) RMS gradient along IRC

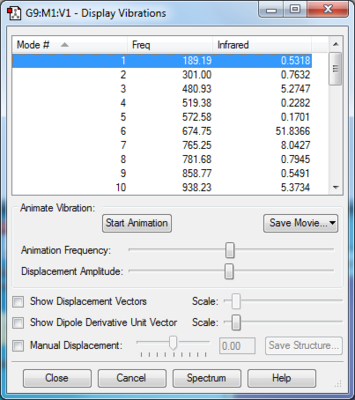
Vibration frequencies:

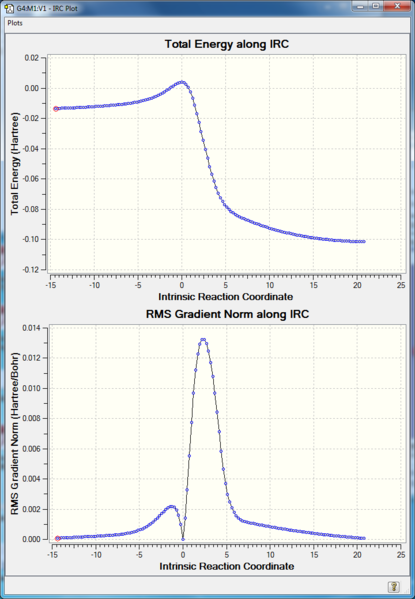
One imaginary frequency of -948.73 cm ^-1 confirming the presence of the transition state (a saddle point- the maximum point on the minimum energy path on the PES)

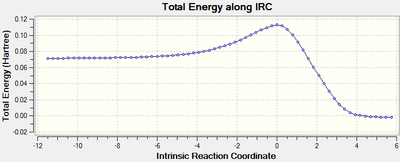
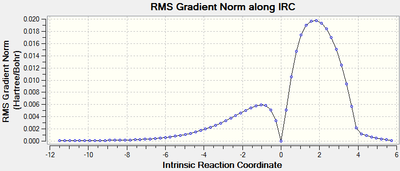
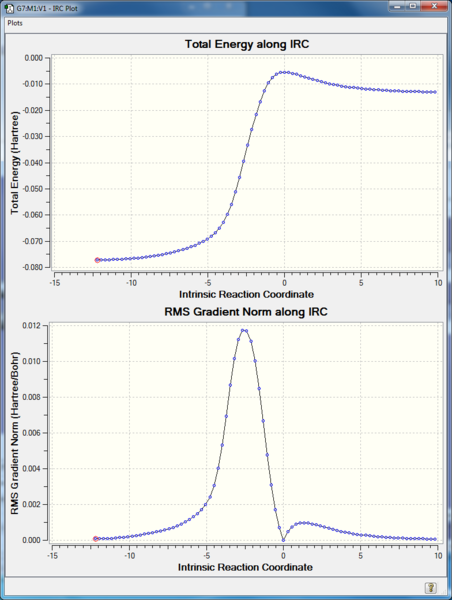
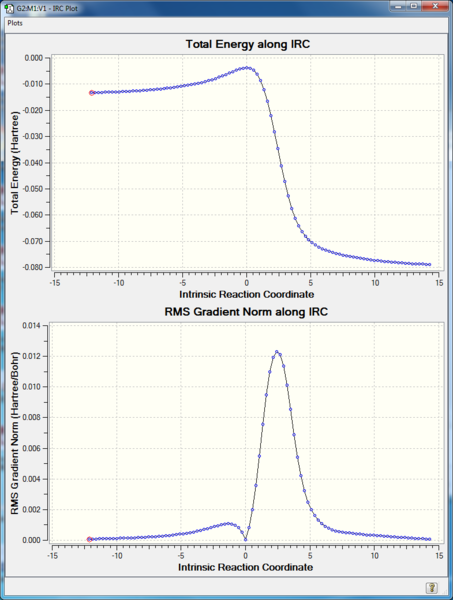
IRC:

RMS gradient Norm of 0 at reactants, products, as well as the transition state. The middle point with 0 gradient corresponding to the maximum energy point on IRC Total Energy curve, indicating transition state.

MO analysis

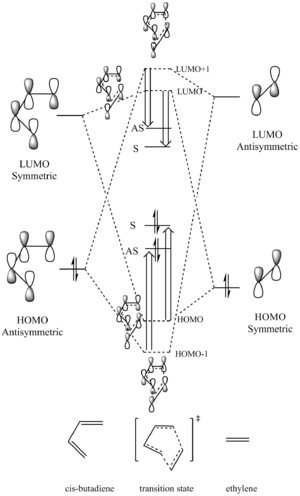
Table 4. MOs of reactants, TS and products

Butadiene

Ethylene

TS(LUMO and HOMO)

TS(LUMO+1 and HOMO-1)

Cyclohexene

LUMO

HOMO

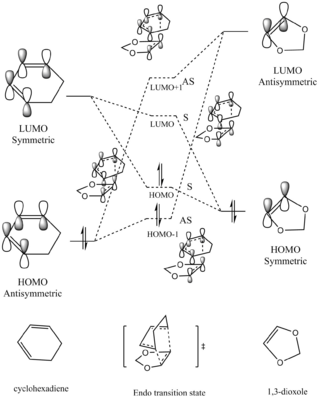
Symmetries and MO interactions

In a reaction, only orbitals with the same symmetry are able to overlap and form new MOs.

The orbital symmetry will be determined by its structure and symmetry label:

for a certain orbital to be symmetric, it will have a plane of symmetry (σ_v plane)

for a certain orbital to be asymmetric, it will have a axis of symmetry (C2 axis)

The orbital overlap integral will be either zero or non-zero with different interactions between symmetric and asymmetric orbitals, zero indicating no interaction between, while non-zero integral indicates existing interaction between two orbitals.The values of orbital overlap integrals are shown as below:

symmetric-antisymmetric interaction: zero

symmetric-symmetric interaction: non-zero

antisymmetric-antisymmetric interaction: non-zero

In this reaction, as we could see from above, the asymmetric orbitals (diene HOMO and dienophile LUMO) will interact with each other to give asymmetric HOMO-1 and LUMO+1 orbitals of the transition state; while the symmetric orbitals (diene LUMO and dienophile HOMO) will interact to give symmetric HOMO and LUMO of the transition state. The HOMO of diene interacts with the LUMO of dienophile to give a better overlap due to a smaller energy gap between these two orbitals. In addition, the antibonding MOs will be stabilised more than that the bonding MOs are stablised.

Among these two interactions, four new MOs will be formed, indicated by the dotted energy levels. However, the true MOs of the TS, indicated by the solid levels, are higher(HOMO and HOMO-1) /lower (LUMO and LUMO+1) than that predicted. This was possibly due to MO mixing, also, because of this MO is of the transition state of the reaction, which is the maximum point on the minimum energy path, therefore, the energy of the MOs will be higher.

In this [4+2] cycloaddition, two new bonds are formed on the same face of the two set of orbitals, in other words, suprafacially. This is in accordance with the Woodward-Hoffmann Rules, where the reaction is only thermally allowed when an odd number is obtained from the equation below:

(4q + 2)s+ (4r)a

=1 + 0

=1

s is for suprafacial, a is for antarafacial, and q and r are two constants representing the number of each component. In this reaction, the diene has 4 suprafacial pi electrons, contributing 0 to the equation; while the dienophile has 2 pi suprafacial electrons, contributing 1 to the equation.

Therefore, the reaction has a sum of 1, indicating this reaction is thermally allowed by Woodward-Hoffmann Rule.

Bond lengths

Table 5. Bond lengths analysis
Bond length values of reactants, TS, and product
Butadiene	Ethylene	Transition state	Cyclohexene

C1=C2 1.335 Å C2-C3 1.468 Å C3=C4 1.335 Å	C1=C2 1.331 Å	C1=C2 1.380 Å C2=C3 1.411 Å C3=C4 1.380 Å C4=C5 2.115 Å C5=C6 1.382 Å C6=C1 2.114 Å	C1-C2 1.500 Å C2=C3 1.338 Å C3-C4 1.500 Å C4-C5 1.540 Å C5-C6 1.541 Å C6-C1 1.540 Å

Table 6. Standard values of C-C bonds and VdW radius
Typical C-C bond lengths and Ver der Waals' radius
C-C bond lengths / Å	Van der Waals' radius of carbon / Å
sp³-sp³ C-C: 1.54 sp³-sp² C-C: 1.50 sp²-sp² C-C: 1.47 sp²-sp² C=C: 1.34	1.7

The bond lengths of the reactants, product, and transition state are shown above in Table 2, while the data of typical C-C bond lengths and the Van der Waal's radius of Carbon are shown in Table 3 above.

Comparing the typical values of the carbon-carbon bonds and the experimental results obtained using Gaussview, we could see that for all three molecules of reactants and products (butadiene, ethylene and cyclohexene) have C-C bond lengths same as or very close to that of the standard values.

Transition State:

Comparison with reactants:

Butadiene fragment:

1. Lengthening of terminal C=C (C1=C2 AND C3=C4)

2. Shortening of middle C-C (C2-C3)

The terminal C=C bonds of butadiene have longer lengths of around 1.380 Å compared that of the typical value of 1.340 Å of sp²-sp² C=C bonds, and the original sp²-sp² C-C bond has a smaller observed value of 1.411 Å (standard value of 1.47 Å).

Ethylene fragment:

1. Lengthening of C=C (C1=C2, shown as C5=C6 in TS)

Between two reactants:

The distances between terminal carbon atoms of butadiene and ethylene in the TS are both at around 2.115 Å, which is much smaller than sum of two carbon atoms' Van der Waals' radius of 3.4 Å. It is also larger than the typical value of sp³-sp³ C-C bond, which shows that the bonds are only partially formed.

All of these bond lengths obtained from Gaussview show that the reaction is at its transition state with two new sp³-sp³ C-C bonds being formed between the terminal carbon atoms, as well as the dissociation of two sp²-sp² C=C bonds into sp²-sp² C-C bonds.

Vibrations

The vibration frequency is -948.73 x^-1 , as shown as the first vibration in Figure 2(a).

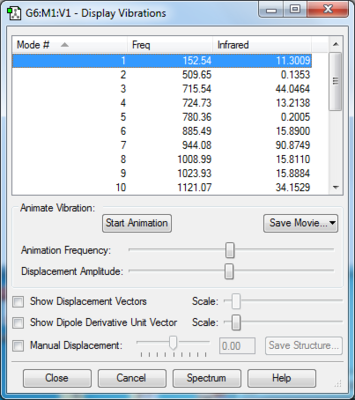
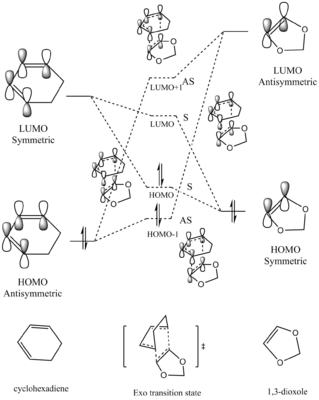
The formation of the two C-C bonds are synchronous, as we could see in the gif in Figure above that the terminals carbon atoms vibrate towards each other to form the new bonds.

Files

Optimised LOG File for butadiene: File:Yz20215 E1 BUTANDIENE MO.LOG

Optimised LOG File for ethylene: File:YZ20215 E1 ETHYLENE MO.LOG

Optimised LOG File for Transition State: File:YZ20215 E1 TS PM6 MO.LOG

Optimised LOG File for cyclohexene: File:YZ20215 E1 CYCLOHEXENE MO.LOG

IRC of the Transition State: File:Yz20215 E1 TS PM6 IRC.LOG

Excercise 2- Diels-Alder reaction of cyclohexadiene and 1,3-dioxole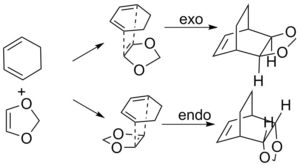

In Exercise 2, the Diels-Alder/[4+2] cycloaddition of cyclohexadiene and 1,3 dioxole was investigated.

Compared with the Diels-Alder reaction in Exercise 1, in E2, both reactants in E2 are consisted of ring structures, rendering them the ability to react both in endo and exo conformations to form two products.

In this excercise, the reactants, products, and Transition states (both endo and exo) were optimised with Method 3 in tutorial using B3LYP/6-31G(d) method in Gaussview software.

In addition, the vibration frequencies, energies and MOs of the molecules were obtained and analysed through optimising the structures.

Optimisation of reactants and products

Table 7. Optimisation of reactants and products using B3LYP/6-31G(d)

Optimisation of Reactants and Products

Reactant: Cyclohexadiene

Reactant: 1,3-dioxole

Product: Endo Product

Product: Exo Product

Structures

Vibration Frequencies

There are no imaginary frequencies for all the reactants and products, as they are at the local minimum point of energy.

Optimisation of Exo and Endo Transition States using B3LYP method

Table 8. Optimisation of TS using B3LYP/6-31G(d)

Optimisation of endo and exo TS

Endo TS

Exo TS

Structures

Vibration Frequencies

In either list of vibration frequency, there is one imaginary frequency, representing a saddle point of Transition State (local maximum point on the minimum energy path on PES).

MO analysis

Table 9. MOs of reactants, TS and products

Endo TS(LUMO and HOMO)

Endo TS(LUMO+1 and HOMO-1)

Exo TS(LUMO and HOMO)

Exo TS(LUMO+1 and HOMO-1)

LUMO

HOMO

Table 10. MO diagrams for both TS
Endo TS	Exo TS
Figure 4(a). MO diagram for Endo TS	Figure 4(b). MO diagram for Exo TS

(Fv611 (talk) There is no point in drawing the same MO diagram twice, but changing the TS schemes. You should have mentioned, showed or discussed the differences between the endo and exo conformations in terms of relative MO energies.)

Normal VS Inverse electron demand

In [4+2] cycloadditions, there are two types of electron demand:

Normal electron demand: Electron-rich diene and Electron-poor dienophile

Inverse electron demand: Electron-poor diene and Electron-rich dienophile

Therefore, in normal electron demand DA reactions, the orbitals of the electron-rich diene will be higher, therefore, favourable interaction occurs between the HOMO of diene and the LUMO of dienophile; while for inverse electron demand reactions, the LUMO of diene will interact with the HOMO of the dienophile.

Generally, carbon-based rings formed in Diels-Alder reactions usually have normal electron demand, while heterocycles formed with DA reaction tends to have an inverse electron demand, as the presence of heteroatoms contributing and changing the energies of the orbtials, leading to different interactions between HOMOs and LUMOs.

In this reaction, due to the presence of a heterocyclic reactant, 1,3-dioxole, it is postulated that the reaction could possibly have an inverse electron demand, therefore, energy calculations were done and their single point energies determined in the following section to confirm the postulation.

Single point energies

Table 11. Single point energies of reactants
Identity	Energy of HOMO/ a.u.	Energy of LUMO/ a.u.	Energy difference between this HOMO and the LUMO of the other reactant/ a.u.
Cyclohexadiene	-0.20554	-0.01711	0.24349
Reactant: 1,3-dioxole	-0.19594	0.03795	0.17883

In this reaction, the energy difference between the HOMO of the dienophile with the LUMO of diene is smaller than that of the other pair, therefore, they will give to a larger overlap of orbitals and more favourable interaciton.

Therefore, we can conclude from the data above that the reaction has an inverse electron demand. This is due to the presence of two oxygen atoms donating their lone pairs, making the dienophile electron rich.

Nf710 (talk) 11:41, 7 March 2018 (UTC) Well done for doing this. You have showed it very clearly.

Energy analysis

Table 12. Energies of reactants, TS, and products
Identity	Energy obtained using B3LYP/6-31G(d) Method/ Hartree/Particle	Energy obtained using B3LYP/6-31G(d) Method/ kJ mol^-1
Reactant: Cyclohexadiene	-233.324375	-612593.193227
Reactant: 1,3-dioxole	-267.068642	-701188.772985
Endo TS	-500.332151	-1313622.16252
Exo TS	-500.329165	-1313614.32277
Endo Product	-500.418702	-1313849.40218
Exo Product	-500.417322	-1313845.77899

Table 13. Activation energies and reaction energies
Product	Activation Energy/ kJ mol^-1	ΔG of reaction/ kJ mol^-1
Endo	159.803692	-67.435968
Exo	167.643442	-63.812778

In a certain reaction, the kinetic product has a lower activation energy therefore will be formed faster, while the thermodynamic product is itself lower in energy, therefore, will be the major product if enough energy is provided to overcome the higher activation barrier.

In this reaction, the activation barrier is lower for the Endo product, hence it is the kinetically favoured product. Furthermore, the ΔG of reaction (which is the energy difference between reactants and the product) is also more negative, indicating a more stable product. Therefore, the Endo product is also the thermodynamically favoured product.

Therefore, the Endo product is both kinetically and thermodynamically favoured product.

Secondary Orbital Interaction

The Endo product being both the kinetic and thermodynamic product is possibly due to the stablisation from secondary orbital interactions between the p orbitals on the oxygen atoms and the π orbitals of the diene, which only takes place when the TS is in Endo conformation.

For Exo conformation, the 1,3-dioxole molecule points outwards and is unavailable to interact with the cyclohexadiene molecule.

The secondary orbital interactions of both the Endo and Exo TS are shown below in Table 9, as well as graph illustration.

Table 14. Secondary orbital interactions

MOs and graph of secondary interaction

HOMO for Endo TS

HOMO for Exo TS

Graph illustrating secondary orbital interactions

Nf710 (talk) 11:44, 7 March 2018 (UTC) Well done for doing this, it was a good section. Everything was consider and nicely tabulated. Your energies are correct and you have come to the correct conclusions. You could have gone into abit more detail in some places such as for the kenetics.

Files

Optimised LOG File for cyclohexadiene: File:Yz20215 E2 cyclohexadiene min.LOG

Optimised LOG File for 1,3-dioxole: File:Yz20215 E2 dioxole min B3LYP.log

Optimised LOG File for Endo Transition State: File:Yz20215 E2 TS endo TS MO 1.log

Optimised LOG File for Exo Transition State: File:Yz20215 E2 TS exo TS.log

Optimised LOG File for Endo product: File:Yz20215 E2 product ENDO B3LYP MIN.LOG

Optimised LOG File for Exo product: File:Yz20215 E2 product EXO B3LYP MIN.LOG

Excercise 3- Diels-Alder vs Cheletropic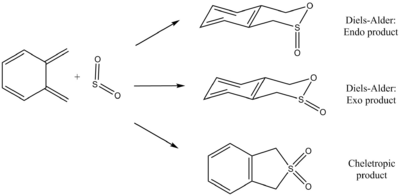

The reaction between xylylene and sulfur dioxide was investigated.

The reaction between the reactants could occur either via a Diels-Alder reaction or cheletropic reaction as shown above in Scheme 3. For the Diels-Alder reaction between two, the product could be formed in an Endo or an Exo conformation.

In this exercise, the reactants, Transition States and products were optimised using PM6 Method using GaussView software. Also, the energies of different species were obtained to determine the activation energy and the energy change of reaction with reaction energy profile plotted. Therefore, the most thermodynamically and the most kinetically favoured product was determined.

Optimisation of Transitions States using PM6 Method

Table 15. Optimisation of TSs using PM6

Optimisation of Transition states

Diels-Alder: Endo TS

Cheletropic

(You need to select the correct frame for JMols. These are just the 15th step of the optimisation Tam10 (talk) 11:49, 6 March 2018 (UTC))

IRC calculations

Table 16. Animations and IRC for TSs
Gif animations and IRC diagrams for Transition States
Diels-Alder: Endo TS	Diels-Alder: Exo TS	Cheletropic TS

Looking at IRC of these three reactions, we could see that the activation barrier of the reaction is quite small, this is due to one of the reactants, xylylene, being very unstable and high in energy.

This is because, according to Huckle's Rule, it has only 8 π electrons, which is (4n) instead of (4n+2), therefore, it is antiaromatic. However, due to structure constraint, both of the dienes are cis in xylylene, which is favourable as no energy expense on converting into trans conformation.

During the reaction, the xylyene part will react with the sulfur dioxide molecule to form a bicyclic ring, containing a benzene ring, which is aromatic and stable. Therefore, making it favourable to form the products.

Activation and Reaction Energy calculations

Table 17. Energies of reactants, TS, and products
Identity	Energy obtained using PM6 Method/ Hartree/Particle	Energy obtained using PM6 Method/ kJ mol^-1
Reactant: Xylylene	0.178047	467.462434
Reactant: Sulfur dioxide	-0.119269	-313.1407834
DA: Endo TS	0.090559	237.762673
DA: Exo TS	0.092076	241.745556
Cheletropic: TS	0.099062	260.087301
DA: Endo Product	0.021698	56.9681033
DA: Exo Product	0.021454	56.3274813
Cheletropic Product	-0.000002	-0.0052510004

Table 18. Activation energies and reaction energies
Product	Activation Energy/ kJ mol^-1	ΔG of reaction/ kJ mol^-1
Endo	83.4410224	-97.3535473
Exo	87.4239054	-97.9941693
Cheletropic	105.7656504	-154.3269016

(These levels of precision are far too high Tam10 (talk) 11:49, 6 March 2018 (UTC))

The energies of the reactants, Transition States, and different products were obtained from the optimised LOG. files in GaussView, and the reaction profile is plotted showing their relative energies with the proceeding of the three reactions.

All TS and product energies are normalised with respect to reactant energy (reactant energy=0). The reaction profile is shown below.

Reaction Profiles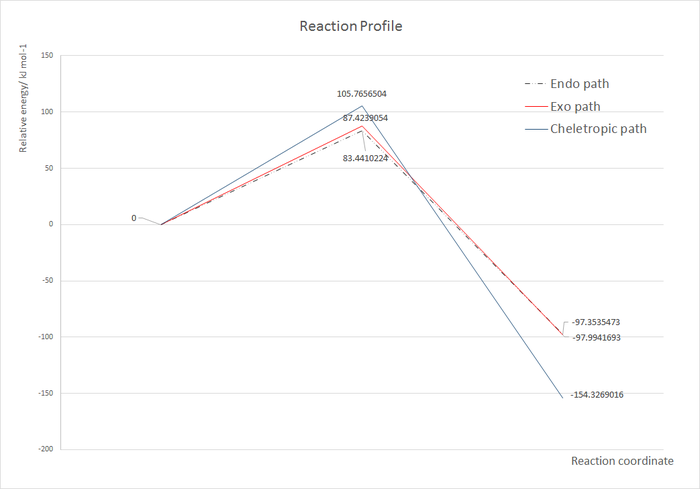

In this profile, we could see that the endo TS is the lowest in energy, therefore will be formed faster compared with other two, and will be the kinetic product of the reaction. The Exo TS has slightly higher but close energy, while the cheletropic TS has the largest activation barrier.

However, if we compare the energies of the products, we could see that the Endo and the Exo products are very close in energy at approximately -98 kJ mol ^-1 , while the cheletropic product is the most stable product with energy of around -154 kJ mol ^-1 . Therefore, if we provide enough energy for the reaction to overcome its activation barrier, the cheletropic product will be the major product as it is the thermodynamic product of the reaction.

Extension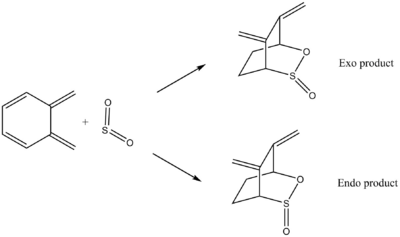

In this reaction, the other diene of xylylene, also in cis conformation, could also reaction with sulfur dioxide to form both the endo and the exo products, and the activation energies and reaction energies of these two reactions are investigated as shown below.

Table 19. Energies of reactants, TS, and products
Identity	Energy obtained using PM6 Method/ Hartree/Particle	Energy obtained using PM6 Method/ kJ mol^-1
Reactant: Xylylene	0.178047	467.462434
Reactant: Sulfur dioxide	-0.119269	-313.1407834
DA: Endo TS	0.102071	267.987431
DA: Exo TS	0.105054	275.819298
DA: Endo Product	0.065615	172.272196
DA: Exo Product	0.067307	176.714542

Table 20. Activation energies and reaction energies
Product	Activation Energy/ kJ mol^-1	ΔG of reaction/ kJ mol^-1
Endo	113.6657804	17.9505454
Exo	121.4976474	22.3928914

These two reaction, are endothermic reactions, with product being higher in energy than that of the reactants. The activation barrier is also around 30 kJ mol ^-1 higher than that of the DA reaction occurring at the other diene, therefore, these two reactions are both thermodynamically and kinetically unfavourable.

Files

Optimised LOG File for Endo TS: File:Yz20215 E3 DA endo TS.LOG

Optimised LOG File for Exo TS: File:Yz20215 E3 DA TS exo TS PM6.log

Optimised LOG File for Cheletropic TS: File:YZ20215 E3 CHE TS.LOG

Extension

Optimised LOG File for Endo TS: File:Yz20215 ext ENDO TS.LOG

Optimised LOG File for Exo TS: File:Yz20215 ext exo TS.log

Conclusion

During the time span of this Transition State Computational Lab, three different pericyclic reactions were investigated.

The reactions were investigated by using PM6 and B3LYP/6-31G(d) methods in GaussView to optimise the reactants, transition states, and the products.

Other information were also extracted from the optimised molecule LOG. files: including vibration frequency calculations and IRC (Intrinsic Reaction Coordinate); bond lengths of the TS, reactants and products; the energies of different species; and the molecular orbitals.

These data were used to analyse the Transition states and the reactions, including confirmation of the TS by presence of one imaginary frequency in vibration frequencies, the activation barrier and energy change of the reaction from the energies of different species, and the MOs to determine the electron demand of a certain Diels-Alder reaction (inverse or normal electron demand).

In addition, the data confirmed that the reactions followed several existing rules and theories: Woodward-Hoffmann rules in Exercise 1, Frontier Molecular Orbital Theory, etc..

These computational methods could be applied to investigate many other pericyclic reactions, where various aspects of data could be obtained and analysed as like shown in this lab.

References

↑ Ot, W. J. (1990). Computational quantum chemistry. Journal of Molecular Structure: THEOCHEM (Vol. 207).
↑ K. Kim, K. D. Jordan (1994). "Comparison of Density Functional and MP2 Calculations on the Water Monomer and Dimer". J. Phys. Chem. 98(40): 10089–10094. doi: 10.1021/j100091a024.
↑ P.J. Stephens, F. J. Devlin, C. F. Chabalowski, M. J. Frisch (1994). "''Ab Initio'' Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields". J. Phys. Chem. 98(45): 11623–11627. doi: 10.1021/j100096a001.

[1] Ot, W. J. (1990). Computational quantum chemistry. Journal of Molecular Structure: THEOCHEM (Vol. 207).

[2] K. Kim, K. D. Jordan (1994). "Comparison of Density Functional and MP2 Calculations on the Water Monomer and Dimer". J. Phys. Chem. 98(40): 10089–10094. doi: 10.1021/j100091a024.

[3] P.J. Stephens, F. J. Devlin, C. F. Chabalowski, M. J. Frisch (1994). "''Ab Initio'' Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields". J. Phys. Chem. 98(45): 11623–11627. doi: 10.1021/j100096a001.

[1]

[2]

[3]