Rep:Y3C Transition States and Reactivity:hjt14

Introduction

Figure 1: A energy profile diagram.

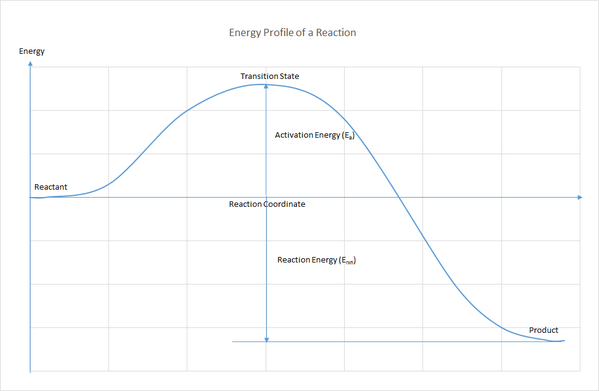
A energy profile of a reaction (see Figure 1) describes how the energy of the system change as the reaction progress along a reaction coordinate. In Figure 1, an arbitrary reaction coordinate is chosen to describe the progress of a reaction in term of energy, from the reactant to the product via a transition state. In fact, the motion of each atom in the chemical species involved in a reaction can be describe using the 3 coordinate system (x,y,z), hence collectively a reaction involving N atoms can be describe using 3N coordinates (in other word 3N degrees of freedom). However, motions like rotation (rotating all the atoms along an axis by the same degree) and translation (moving all atoms by the same translation vector) species do not contribute to the change in energy and thus need to be factored out. As a result, we are left with 3N-6 vibrational coordinates to describe the progress of a reaction. When a reactants approach each other (This is not translation as not all the atoms are moving in the same direction and magnitude), some bonds are being broken and some are being formed. In term of nuclear motions, the nuclei involved in bond formation or bond cleavage are moving away from the equilibrium positions and this cause the energy of the system to rise, just like how the energy of a harmonic oscillator increases as it moves away from equilibrium bond distance. Then the nuclei move into new equilibrium position in the product and this cause the energy of the system to drop, just like how the energy of a harmonic oscillator decreases as it moves toward the equilibrium bond distance. In between the rise and fall of energy, there will be a point where the energy is maximum and this is where the transition state sit. It is challenging to perceive graph of more than 3 dimensions and this explains why energy profile of reaction is generally represented using 2D or 3D graph. In 2D graph, we will obtain an energy line and in 3D graph the reaction progress can be described using a surface know as potential energy surface.

Reactant and product are represented as the energy minima on the potential energy surface. In between the energy minima there is saddle point where the system have to cross to go from the reactant to the product. What a saddle point mean is that the energy is maximum along one vibrational coordinate and minimum along other vibrational coordinates. Stationary point like this on an energy surface can be located using the first derivatives of energy with respect to all the vibrational coordinates and these derivatives correspond to the forces acting on atoms along the corresponding vibrational coordinate. At energy maxima and minima, the forces acting on atoms are zero. To distinguish maxima from minima, secondary derivatives with respect to the vibrational coordinates can be used. At energy maxima, the secondary derivative will be negative; at energy minima the secondary derivative will be positive. In addition, the secondary derivative is the the force constant of the harmonic oscillator. In diatomic molecule, the force constant is related to the frequency of vibration via following equation:

Figure 2: An equation which relates vibrational frequency of diatomic molecule to the force constant.

In this lab, 3 Diels-Alder reactions were studied using computational chemistry software, Gaussian. This software was used to optimise the geometry of each species (reactant, transition state, and product) by solving the Schrodinger equation and calculating the force constants along all the vibrational coordinates to locate the energy maxima (transition state) and energy minima (product and reactant).

Nf710 (talk) 16:07, 20 January 2017 (UTC) Good understanding of the normal modes of vinration (modes that cannot couple to each other). Nice intro good unstanding of TSs, Some intro about the levels of theory would have been nice.

Calculations

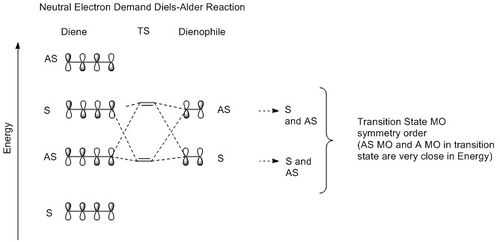
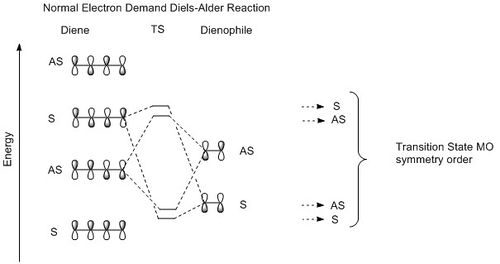
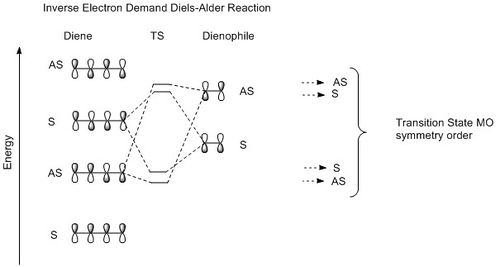
Depending on the relative position of the frontier orbitals of diene and dienophile along an energy scale, Diels-Alder reaction can be classify as neutral, normal or inverse electron demand. (See Figure 3) In each case, the TS MO symmetry order is different and this gives us an shorthand to classify the Diels-Alder reaction simply by looking at the TS MOs symmetry order. (symmetry element under study: mirror plane; S= symmetrical; AS= asymmetrical; - See Figure 6)

Figure 3:MO diagrams above show how the frontier orbitals of reactants interact and also the TS MO symmetry order in each case.

Exercise 1: Diels-Alder Reaction of Butadiene with Ethylene

In this part of the lab, a Diels-Alder reaction between butadiene and ethene was studied computationally. Figure 4 below shows the arrow pushing diagram for the Diels-Alder reaction between a butadiene and an ethene and figure 5 shows the MO diagram. Ethene, butadiene and transition state (TS) were optimised using semi-empirical method and PM6 basis set. The frontier orbitals of each species are shown in Table 1. By looking at the TS MOs symmetry order, one can deduces that this reaction is inverse electron demand.

Figure 4: Diels-Alder reaction between a butadiene and an ethene.

Figure 5: MO diagram of Diels-Alder reaction between a butadiene and an ethene.

Table 1: Frontier Orbitals of s-cis butadiene and ethene					Table 2: Frontier Orbitals of Transition State of Diels-Alder Reaction between Butadiene and Ethene
Species	Molecular Orbital		Symmetry		Species	Molecular Orbital		Interating MO pair	Symmetry
s-cis butadiene	HOMO		Asymmetric		Transition State	LUMO+1		Antibonding interaction between s-cis butadiene HOMO and ethene LUMO	Asymmetric
	LUMO		Symmetric			TS LUMO		Antibonding interaction between s-cis butadiene LUMO and ethene HOMO	Symmetric
Ethene	HOMO		Symmetric			TS HOMO		Bonding interaction between s-cis butadiene LUMO and ethene HOMO	Symmetric
	LUMO		Asymmetric			TS HOMO-1		Bonding interaction between s-cis butadiene HOMO and ethene LUMO	Asymmetric

Figure 6: Plane of symmetry used to to distinguish the symmetry of MO.

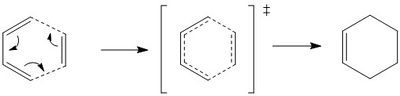
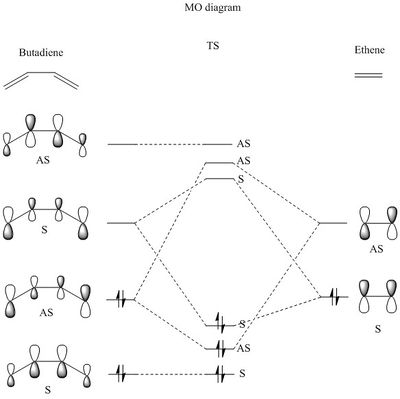
When butadiene and ethene are brought together along the reaction coordinate, the HOMO and LUMO of butadiene interact with HOMO and LUMO of ethene to form new MOs. To interact, the pair of interacting MOs need to have the same symmetry. The symmetry under question in this case is the plane of symmetry depicted in Figure 6. The HOMO of butadiene and the LUMO of ethene are both asymmetrical and they interact to form new bonding and antibonding TS MOs as shown in Table 2; the LUMO of butadiene and HOMO of ethene are symmetrical and they interact with each other to form new bonding and antibonding TS MOs as shown in Table 2.

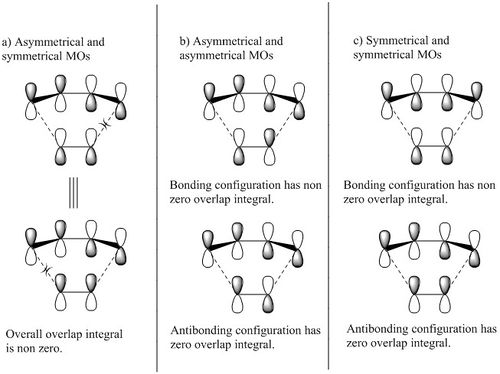
The symmetry requirement in Diels-Alder reaction is illustrated in figure 7 and table 2. When a symmetrical MO interacts with an asymmetrical MO, antibonding and bonding configurations are equivalent to each other. Within a configuration, the bonding interaction has a positive overlap integral and the antibonding interaction has a zero overlap integral, hence the overall overlap integral is non zero. Besides, the stabilising effect of bonding interaction is cancel out by the destabilising effect of the antibonding interaction. Overall, there is no interaction between symmetrical MO and asymmetrical MO. For symmetrical pair and asymmetrical pair, the bonding configuration has non zero overlap integral and are overall stabilised, whereas the antibonding configuration has zero overlap integral and overall destabilised. In the HOMO-LUMO region, usually only the bonding orbitals are populated and result in overall stabilisation.

Figure 7: Symmetry requirement for molecular orbital interactions.

The following graph show how the inter-nuclear distance between carbon atoms change as the reaction progress from product to reactant (from left to right).

Figure 8: Number labelled reactants.

Figure 9: Graph of inter-nuclear distance against reaction coordinate.

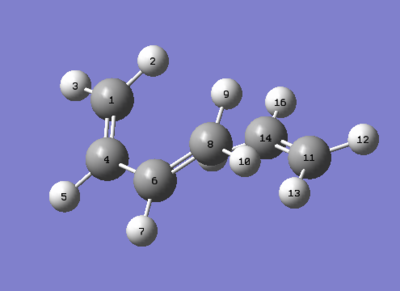
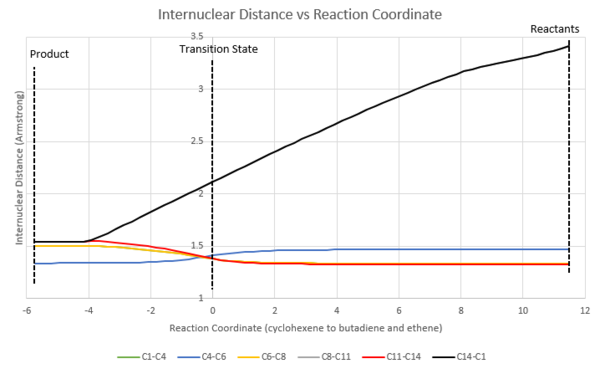
Reactant		TS		Product		Literature Values for C-C bond length
Bond	Bond length (Armstrong)	Bond	Bond length (Armstrong)	Bond	Bond length (Armstrong)
C1-C4	1.33539	C1-C4	1.37979	C1-C4	1.50085	sp3C-sp3C	1.54
C4-C6	1.46833	C4-C6	1.41110	C4-C6	1.33695
C6-C8	1.33539	C6-C8	1.37977	C6-C8	1.50079	sp3C-sp2C	1.50
C8-C11	NA	C8-C11	2.11484	C8-C11	1.53716
C11-C14	1.32737	C11-C14	1.38178	C11-C14	1.53464	sp2C-sp2C	1.48
C14-C1	NA	C14-C1	2.11466	C14-C1	1.53711

From reactants to product,:

• the bond order of C1-C4, C6-C8, and C11-C14 decrease from 2 to 1 and hence the bonds elongate.
• the bond order of C4-C6 changes from 1 to 2 hence the bond shortens.
• sigma bond is formed between C8 and C11, and C1 and C14, therefore the inter-nuclear distances decrease drastically.
• the sigma bonds are forming at the same time. Meaning that at any point along the reaction coordinate, the forming bonds share the same length and such reaction can be describe as synchronous.

At transition state,:

• the C-C bond length fall in between the C-C bond length in product and the C-C bond length in reactant (except C8-C11 and C14-C1).
• (for C8-C11 and C14-C1) the C-C bond length is in between 3.40 Armstrong (2*carbon van der Waal's radius and literature value for carbon van der Waal's radius: 170 Armstrong) and the sp³C-sp³C bond length.

Nf710 (talk) 16:32, 20 January 2017 (UTC) Excellent first section

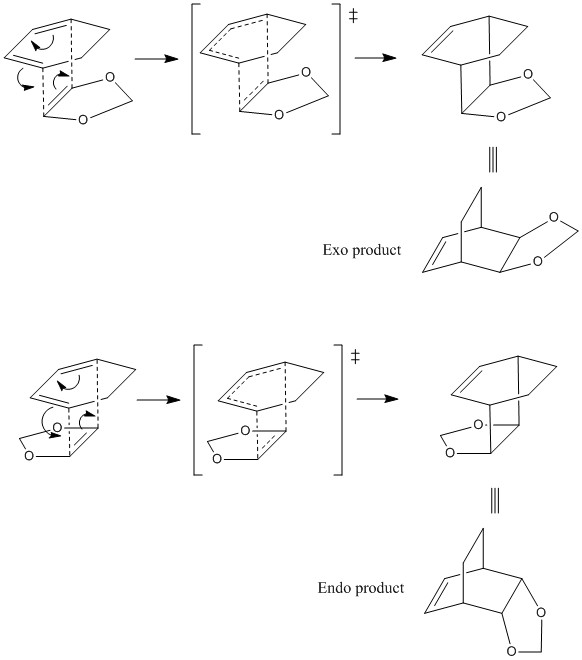
Exercise 2: Diels-Alder Reaction of Cyclohexadiene and 1,3-Dioxole

The following figure shows the reaction scheme for Diels-Alder reaction between cyclohexadiene and 1,3-dioxole and also the transition state leading to endo and exo products.

Figure 10: Diels-Alder reaction between cyclohexadiene and 1,3-dioxole

First, the geometry of reactants were optimised using semi-empirical method, PM6 basis set and then DFT method, B3LYP631Gd basis set. Using the optimised reactants, guess TSs were constructed and optimised using semi-empirical method, PM6 basis set and then DFT method, B3LYP631Gd basis set. After which, IRC calculation were ran for endo and exo TSs to confirm that the TSs do lead back to the correct reactants and products. The results are tabulated in table 3 (reactants) ,table 4 (endo transition state) and table 5 (exo transition state).

Table 3: Frontier Orbitals of Cyclohexadiene and 1,3-Dioxole					Table 4: Frontier Orbitals of Endo Transition State of Diels-Alder Reaction between Cyclohexadiene and 1,3-Dioxole					Table 5: Frontier Orbitals of Exo Transition State of Diels-Alder Reaction between Cyclohexadiene and 1,3-Dioxole
Species	Molecular Orbital		Symmetry		Molecular Orbital		Interating MO pair	Symmetry		Molecular Orbital		Interating MO pair	Symmetry
Cyclohexadiene	HOMO		Asymmetric		Endo TS LUMO+1		Antibonding interaction between cyclohexadiene HOMO and 1,3-dioxole LUMO	Asymmetric		Exo TS LUMO+1		Antibonding interaction between cyclohexadiene HOMO and 1,3-dioxole LUMO	Asymmetric
	LUMO		Symmetric		Endo TS LUMO		Antibonding interaction between cyclohexadiene LUMO and 1,3-dioxole HOMO	Symmetric		Exo TS LUMO		Antibonding interaction between cyclohexadiene LUMO and 1,3-dioxole HOMO	Symmetric
1,3-Dioxole	HOMO		Symmetric		Endo TS HOMO		Bonding interaction between cyclohexadiene LUMO and 1,3-dioxole HOMO	Symmetric		Exo TS HOMO		Bonding interaction between cyclohexadiene LUMO and 1,3-dioxole HOMO	Symmetric
	LUMO		Asymmetric		Endo TS HOMO-1		Bonding interaction between cyclohexadiene HOMO and 1,3-dioxole LUMO	Asymmetric		Exo TS HOMO-1		Bonding interaction between cyclohexadiene HOMO and 1,3-dioxole LUMO	Asymmetric

Cyclohexadiene	1,3-Dioxole	Endo TS	Endo Product	Exo TS	Exo Product

(Useful JMols with vibrations and surfaces, as some interactions are hard to see in the diagrams above Tam10 (talk) 10:40, 4 January 2017 (UTC))

By looking at the order of the symmetry of TS MOs, one can deduce that the Diels-Alder reaction between cyclohexadiene and 1,3-dioxole is inverse electron demand. This is expected because the lone pair on the oxygen atom in 1,3-dioxole can delocalise into the pi system, rising the energy of HOMO of dienophile. Hence, the energy gap between diene LUMO and dienophile HOMO decreases and the energy gap between diene HOMO and dienophile LUMO increases. Consequently, the orbital interactions between diene and dienophile during Diels-Alder reaction are dominated by diene LUMO and dienophile HOMO interaction.

Exo product is generally regarded as the thermodynamic product because there are less unfavourable steric interactions in exo product than in endo product. However, endo product is generally regarded as the kinetic product because secondary orbital interactions in the transition state leading to endo product lower the energy of the endo transition state and also the activation energy. Consequently, endo product is formed faster than exo product. The thermochemistry data, obtained from the gaussian output log file of reactants, transition states and products (all are optimised from IRC output) at DFT B3LYP631Gd caculation level, were summarised in following table. These data were used to calculate the activation energy and reaction energy of exo and endo pathways.

Thermochemistry  data ( obtained from DFT B3LYP631Gd optimised reactant, product, TS from IRC output ):				
				
Temperature/ K: 	    298.150 Kelvin	   |	          0 Kelvin	
                                                   |
	          Sum of electronic and thermal    |   Sum of electronic and zero-
                  free Energies (Hartree/Particle) |   point energies (Hartree/Particle)	
                                                   |
Exo reactants     :         -500.381626	           |	       -500.339315
Exo TS            :         -500.329168            |	       -500.294732
Exo Product       :  	    -500.417314	           |	       -500.384595	
Endo reactants    :  	    -500.381519	           |	       -500.338832	
Endo TS           :         -500.332154	           |	       -500.297145		
Endo product      :         -500.420015	           |	       -500.387295	     	
                                                   |
		                                   |		
Exo pathway         	      kJ/mol	           |	          kJ/mol	
Activation barrier: 	     137.728479	           |	        117.0526665	
Reaction energy	  :          -93.698844            |	       -118.8826400	
                                                   |
                                                   |
		                                   |		
Endo pathway	              kJ/mol	           | 	          kJ/mol	
Activation barrier: 	     129.6078075	   |	         109.4492185	
Reaction energy	  :         -101.0712480	   |            -127.2396065	

Figure 11: Energy profile for exo and endo Diels-Alder reaction between cyclohexadiene and 1,3-dioxole.

Looking at the energy profile, the endo product is indeed the kinetic product as it has lower activation barrier. The secondary orbital interaction which lowers the energy of transition state are observed in the MO of transition state and is shown in Figure 12 (Only secondary orbital interaction in occupied MO is shown because unoccupied MO which exhibit secondary orbotal interaction do not contribute to stabalisation of TS. Interestingly, endo is also the thermodynamic product as it is lower in energy than exo product. This is probably due to the fact that the steric interaction is weak and do not contribute strongly to the energy of product.

Figure 12: Secondary orbital interaction in endo TS.

Nf710 (talk) 16:41, 20 January 2017 (UTC)Good understanding of SSO. Your energies are slightly out however but you still have the correct conclusion

Exercise 3: Diels-Alder and Cheletropic Reactions of Xylylene and Sulfur Dioxide

In this part of the computational lab, guess exo and endo transition state of Dels-Alder reaction and guess transition state of cheletropic reaction were obtained by distorting the corresponding optimised products. The guess TSs were then optimised and IRC were carried out. After which the reactants and products from IRC output were optimised and thermochemistry data of each reaction were calculated. All the calculations were done using semi-empirical method and PM6 basis set. The gif file of each IRC output are tabulated in table 6. One feature that was common among all reaction pathway is the rearomatisation of the cyclohexadiene moeity during the course of the reaction.

Reactants
Xylylene	Sulfur Dioxide

Cheletropic Pathway
Transition State	Product

Exo Pathway
Transition State	Product

Endo Pathway
Transition State	Product

Table 6: Gif file of IRC output

Endo Pathway (reactant to product)	Exo Pathway (product to reactant)	Cheletropic Pathway (reactant to product)

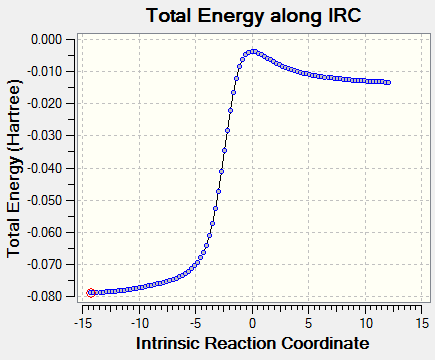
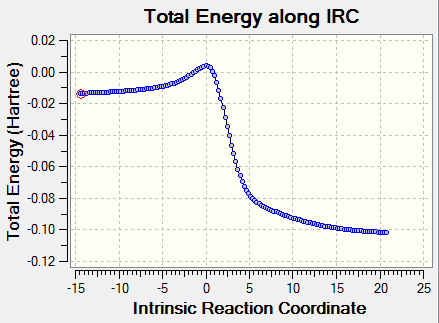
The thermochemistry data, obtained from the gaussian output log file of reactants, transition states and products (all species are from optimised IRC output except exo reactants) at semi-empirical PM6 caculation level, were summarised in following table. These data were used to calculate the activation energy and reaction energy of exo, endo and cheletropic pathways.

Thermochemistry  data ( obtained from semi-empirical PM6 optimised reactant, product, TS from IRC output except exo reactants ):				
				
Temperature/ K: 	        298.150 Kelvin	       |	          0 Kelvin	
                                                       |
	              Sum of electronic and thermal    |   Sum of electronic and zero-
                      free Energies (Hartree/Particle) |   point energies (Hartree/Particle)	
                                                       |
Exo reactants*       :         0.060496	               |	       0.116965	
Exo TS               :         0.092077                |	       0.128171	
Exo Product          :         0.021455	               |	       0.056644	
Endo reactants       :         0.067926	               |	       0.114802	
Endo TS              :         0.090560	               |	       0.126589	
Endo product         :         0.021705	               |	       0.057503	                                                
Cheletropic reactants:         0.068174                |               0.114815
Cheletropic TS       :         0.099062                |               0.135560
Cheletropic Product  :        -0.000002                |               0.034556
                                                       |
		                                       |		 
Exo pathway         	         kJ/mol	               |	         kJ/mol	
Activation barrier   : 	      82.9159155	       |	      29.421353	
Reaction energy	     :      -102.5021455               |	    -158.3727855	
                                                       |                                             
		                                       |		
Endo pathway	                 kJ/mol	               | 	         kJ/mol	
Activation barrier   :	      59.425567	               |	      30.9467685	
Reaction energy	     :      -121.3532355	       |            -150.4385245	
                                                       |
                                                       |   
Cheletropic pathway	         kJ/mol	               | 	          kJ/mol	
Activation barrier   :	       81.096444	       |	       54.4659975	
Reaction energy	     :       -178.996088	       |             -210.7200045

* obtained by summing energy of individually optimised reactant molecule because it was very difficult to optimised the reactant from IRC output.

(You must be consistent in your calculations. For your reactants, you've added a contribution of about 20 kJ/mol. This has pushed up your exo barrier and reaction energy Tam10 (talk) 10:40, 4 January 2017 (UTC))

Figure 13: Energy profile for endo, exo and cheletropic pathway.

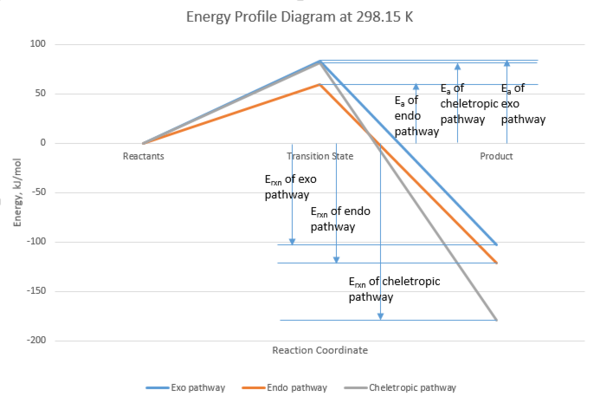
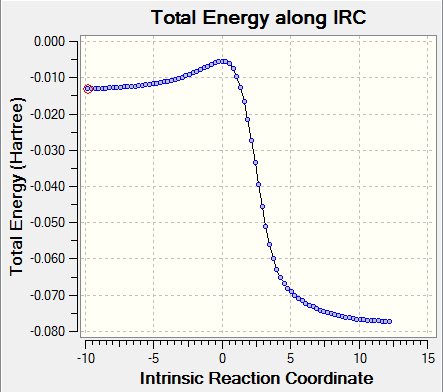
From the energy profile (Figure 13), one can conclude that cheletropic product is the thermodynamic product and endo product is the kinetic product. If the reaction between xylylene and sulfur dioxide is irreversible, the product which forms fastest will be the major product, and in this case it is endo product.

(Not enough text. What about the instability of xylylene? Tam10 (talk) 10:40, 4 January 2017 (UTC))

Conclusion

Exercise 1: The Diels-Alder reaction between butadiene and ethene is synchronous as bond is forming at the same time. During the course of the reaction, bond that is changing bond order will experience change in bond length, i.e. increase in bond order will cause the bond length to decrease and vice versa.

Exercise 2: The Diels-Alder reaction between cyclohexadiene and 1,3 dioxole is inverse electron demand. Endo product of the reaction is the kinetic and also the thermodynamic product due to secondary orbital interaction depicted in figure 12 and small steric effect.

Exercise 3: Reaction between xylylene and sulfur dioxide can occur via 3 pathways, namely endo, exo and cheletropic. Kinetic product of the reaction is endo product and thermodynamic product is cheletropic product.