Transition State Structures

Introduction

In this experiment, the transition states of several pericyclic reactions where investigated using computational techniques to acquire information about the kinetics and thermodynamics of these reactions, and analyse the molecular orbitals of these chemical systems.

A potential energy surface (PES) is a plot of the potential energy of a chemical system as a function of two or more reaction coordinates. The number of dimensions of a PES is 3N-6 (where N is the number of atoms in the molecular system being considered). In the PES the first derivative of the energy, physically representing the gradient, which is related to the force acting on the atoms whilst the second derivative, a physical measure of the curvature, is related to the force constants, k. The values of k can then be used to calculate the vibrational frequencies for each of the 3N-6 modes.

A minimum point (zero first derivative, positive second derivative) along a reaction coordinate, of the PES of the molecular system of interest, corresponds to a stable species in the reaction. This could potentially be a reactant, product or intermediates of the reaction mechanism. A transition state (TS) is a maximum point (zero first derivative, negative second derivative) along the reaction coordinate, of the PES. It is also possible that the TS for a particular reaction pathway might be a saddle point on the PES which has a zero first derivative and second derivative that is positive in some directions and negative in others. The reaction path taken can be identified form the potential energy surface by keeping the system in equilibrium whilst varying the reaction coordinates, thus elucidating the minimum energy pathway linking reactants and products via a transition state; known as the intrinsic reaction coordinate (IRC).

Nf710 (talk) 10:42, 6 March 2018 (UTC) Some confusion here, A TS is always a first order saddle point. and always only has 1 dimension of negative curvature. This info is obtained by diagonalising the force constant and looking a the eigen values.

During this experiment two optimisation methods on Gaussian were used; the semi-empirical PM6 method and the density functional theory (DFT) based B3LYP. Both optimization methods are based on the Hartee-Fock model, which accounts for electron-electron interactions by assuming that any given electron in a molecule only experiences an average field from the other electrons. The relatively simpler non-ab initio PM6 method uses pre-determined empirical data in its estimation of electron density, and therefore is a relatively fast method. The B3LYP method uses 6-31(G) basis set which is essentially a mathematical representation of the atomic orbitals which make up the molecular orbitals of the molecular system being studied (i.e. LCAO theory). The B3LYP method involves the evaluation of an exchange correlation parameter term, which more accurately represents electron-electron repulsions. The purpose of these methods was to solve the time independent Schrödinger equation at each point as reaction coordinates are varied and calculate the corresponding energy, and the subsequent first and second derivatives of the energy with respect to the specific position on the PES. This allows determination of an optimised geometry. Optimised in the sense of either being a minimum and therefore a stable species involved in the reaction (by performing a minimisation calculation) or a TS (by choosing a TS(Berny) calculation). In the case of the TS optimisation calculation must have force constants calculated only once, and usually include the Gaussian keyword opt = noeigen (which in the case of multiple negative frequencies being found will prevent the calculation from terminating).

Nf710 (talk) 10:52, 6 March 2018 (UTC) Fairly good understanding, but you could have added some equations to break up the text. You have clearly read beyond the script.

Gaussian was used to locate the TSs of the reactions studied. Several different methods were employed to find to locate the TS. Firstly, a guess-TS was built in GaussView and then optimised directly to the TS, whilst this is the fastest approach it is also the least reliable and to be of any use some prior knowledge of the TS is requires. Secondly, a guess-TS could have the interatomic distances between the atoms which are broken or formed during the reaction step fixed (‘frozen coordinates’), and then preform a minimisation calculation, before optimising to the TS. Also, a third method used involved minimising the structure of the reactants, or products, and then altering the structure and freezing the coordinates to obtain a more accruate guess-TS, which can then be optimised to the TS.

Exercise 1: Diels-Alder reaction of butadiene with ethylene

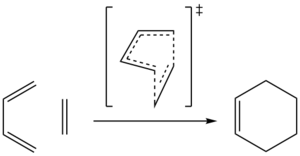
Figure 1: Reaction scheme of for the Diels-Alder reaction between ethylene and butadiene to form cyclohexane.

(Fv611 (talk) Great work across the whole exercise. Well done!)

For this exercise the Diels-Alder reaction between ethylene and butadiene was studied (see figure 1). The method used was to first optimise the cyclohexene product to a minimum and then the two C-C bonds formed during the Diels-Alder were broken and frozen at a distance of 2.2 Å. This structure was then first minimised and then optimised to the TS.

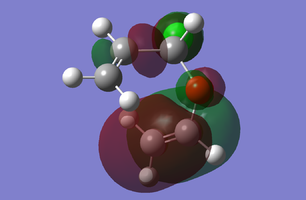
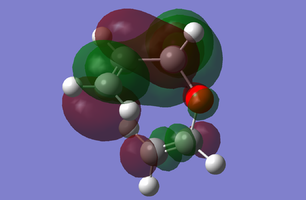
MO Diagram of transition state

Figure 2: MO Diagram of the transition state formed from the Diels-Alder reaction between ethylene and butadiene. All MOs labelled with relative energy and described as symmetric, (s), and antisymmetric, (a).

The above figure illustrates the simplified molecular orbital (MO) diagram for the TS of the Diels-Alder reaction between ethylene and butadiene. An IRC calculation was run on the optimised TS for this reaction and from the log file initial frame, corresponding to the reactants an energy calculation reactants. This was necessary to obtain the relative energy levels of the MOs of the reactants and the TS which were comparable.

From the MO diagram (figure 2) it can be seen that the MOs of the TS formed from the linear combination of the frontier molecular orbitals of ethylene and butadiene are quite high in energy. Although this is to be expected since the transition state is the highest energy point along the reaction coordinate, and therefore the theoretical activated complex species which exists at this point, should be destabilised relative to the reactants.

HOMO and LUMO of reactants and resultant MOs in transition state

The table below displays the HOMOs and LUMOs of ethylene and butadiene as well as the four MOs of the TS which form because of the linear combination of the reactants frontier MOs, which are the same as does demonstrated in the above MO diagram. HOMO-1 (MO16) of the TS is the bonding orbital resulting from the net in-phase interaction (constructive interference) between the HOMO of butadiene and the LUMO of ethylene, and the LUMO +1 (MO19) of the TS is the corresponding antibonding orbital formed via an out-of-phase interaction (net destructive interference) between the butadiene HOMO and ethylene LUMO. The TS HOMO (MO17) is the bonding orbital formed because of the in-phase interaction between the ethylene HOMO and butadiene LUMO, with TS LUMO (MO18) being the antibonding orbital formed by the out-of-phase interaction between ethylene HOMO and butadiene LUMO.

Name

MO Jmol

Comments

HOMO of ethylene

MO 6

Relative energy: -0.39228

Symmetric

LUMO of ethylene

MO 7

Relative energy: 0.04256

Antisymmetric

HOMO of butadiene

MO11

Relative energy: -0.35166

Antisymmetric

LUMO of butadiene

MO 12

Relative energy: 0.01103

Symmetric

HOMO - 1 Transition state

MO 16

Relative energy: -0.32755

Antisymmetric formed as the 'bonding' MO form the interaction of the LUMO of ethylene and the butadiene HOMO

HOMO Transition state

MO17

Relative energy: -0.32532

Symmetric formed as the 'bonding MO' from the interaction of the ethylene HOMO and the Butadiene LUMO

LUMO Transition state

MO 18

Relative energy: 0.01733

Symmetric formed as the 'antibonding MO' from the interaction of the ethylene HOMO and the Butadiene LUMO

LUMO + 1 Transition state

MO 19

Relative energy: 0.0366

Antisymmetric formed as the 'antibonding MO' from the interaction of the ethylene LUMO and the Butadiene HOMO

Examination of the MOs of the TS exemplifies the principle of conservation of orbital symmetry; that is that only orbitals of the same symmetry can linearly combine. This can be explained by considering the orbital overlap integral, as for an overlap between orbitals of different symmetry (i.e. symmetric-asymmetric interaction) there will be equal amounts of in-phase (constructive) overlap and out-of-phase (destructive) overlap leading to a net zero overlap, hence the overlap integral for such an interaction is therefore zero. The overlap of orbitals of the same symmetry (i.e. symmetric-symmetric and asymmetric-asymmetric) have a non-zero overlap integral, as there will be either a net in-phase or out-of-phase interaction. The LUMO of ethylene and the butadiene HOMO are both asymmetric and therefore can linearly combine to generate the two asymmetric MOs of the TS (MO16 and MO19). Conversely, the Ethylene HOMO and Butadiene LUMO are symmetric can linearly combine to give the two symmetric MOs of the TS (MO17 and MO18).

C-C bond lengths

For optimized reactants:

Throughout the course of the Diels-Alder reaction the bond lengths of all C-C bonds change due to the changes in hybridisation of some of the carbons and the changes in all the bond orders, and as two additional sigma bonds are formed by the cycloaddition. The data listed below demonstrates the changes in bond lengths that occur on going from reactants to TS to product.

Ethylene C-C bond length = 1.33 Å

Butadiene central C-C bond length = 1.46 Å

Butadiene terminal C-C bond lengths = 1.34 Å

At the optimised transition State:

Ethylene C-C bond length = 1.38 Å

Butadiene central C-C bond length = 1.41 Å

Butadiene terminal C-C bond lengths = 1.38 Å

Partly formed new C-C bonds = 2.11 Å

For the optimized product

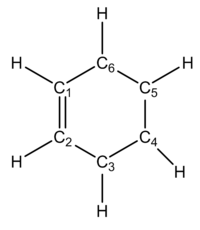
Ethylene C-C bond length (C4-C5) = 1.54 Å

Butadiene central C-C bond length (C1-C2)= 1.34 Å

Butadiene terminal C-C bond lengths (C2-C3 & C6-C1) = 1.50 Å

Newly formed bonds (C3-C4 & C5-C6) = 1.54 Å

Typical C-C bond lengths:

C(sp³)-C(sp³) = 1.54 Å

C(sp²)-C(sp²) = 1.50 Å

C(sp³)-C(sp²) = 1.34 Å

Carbon Van der Waals radius = 1.70 Å

The C-C bond lengths in the optimised reactants and product are as expected. The C-C bond ethylene is 1.33 Å (very close to close to the typical alkene C-C sp²-sp² double bond length of 1.34Å). During this reaction, the carbon atoms (carbon atoms 4 and 5, see figure 3) of the ethylene dienophile goes from a double bond C(sp²)-C(sp²) to a single C(sp³)-C(sp³) and therefore lengthens as the reaction progresses. The C4-C5 bond length is 1.38Å which is intermediate between the shorter C-C single bond length in the optimised TS. The C4-C5 bond length in the cyclohexene product 1.54 Å, very similar typical C(sp³)-C(sp³) bond lengths. The newly formed C-C bonds in product is also at the typical C(sp³)-C(sp³) bond length and in the TS the interatomic distances between these carbon atoms (C3-C4 and C5-C6) is within the two times the van der Waals radius of carbon which indicates that there is an interaction between these two carbon atoms in the TS of the [4+2] cycloaddition. The central C-C bond of butadiene is broadly similar to typical values for a C-C single bond between two sp²hybridised carbon atoms (1.50 Å). This bond becomes progressively shorter in the reaction as in the TS the value is intermediate between the C-C bond length in the reactant and that of the C=C of an alkene, and this illustrates how the two carbon atoms come closer together in this reaction to form the π bond in the cyclohexene product (C1-C2 bond length). Like the ethylene C-C bond, the terminal C-C bond of butadiene has the typical alkene C=C bond length, and this bond lengthens as the reaction progresses with a values in intermediate of the short the C=C alkene bond and that of the typical C(sp³)-C(sp²) single bond length, at the transition state. In the product, this C-C bond length (C2-C3 and C1-C6) is as expected for a typical C(sp³)-C(sp²) length (1.50 Å).

Vibration at the reaction path for the transition state

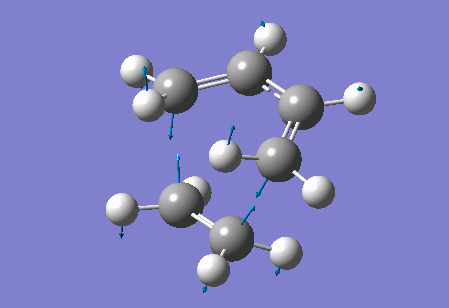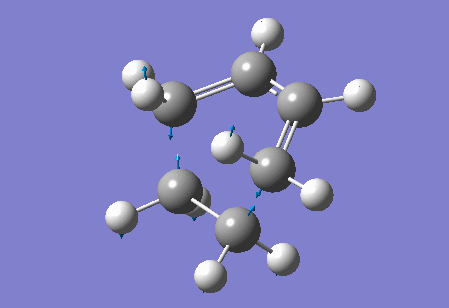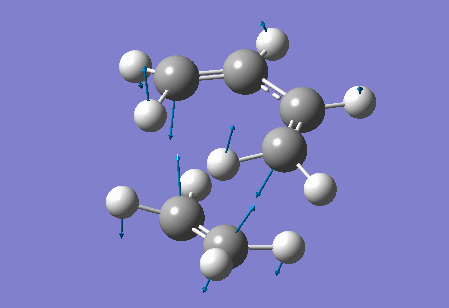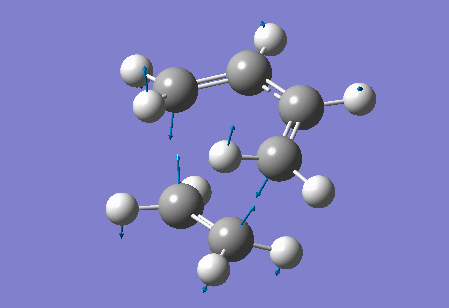IRC animation
Figure 4 Animation of vibration of TS at the reaction path

The negative frequency at -949.20 cm^-1 in the TS of this reaction corresponds to the vibration at the reaction path. This negative vibration is due to the negative force constant at the TS (since the force constant is related to the second derivative and at the TS, a maximum point along the reaction path, the second derivative is negative). This vibration is animated above, figure 4, and appears to represent bond formation, and provides evidence that the bond formation in this reaction is synchronous and therefore that the cycloaddition reaction is concerted.

LOG files

Optimised ethylene = File:ETHENE OPT MIN.LOG-y3as6115

Optimised butadiene = File:Y3as6115BUTADIENE OPT MIN.LOG

Optimised TS = File:ETHENE-BUTADIENE TS OPT.LOGy3as6115

Optimised cyclohexene = File:AS6115CYCLOHEXADIENE MIN.LOG

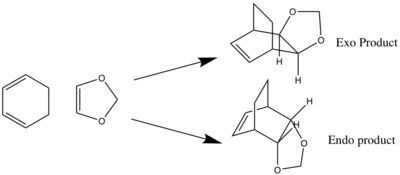
Excercise 2: Diels-Alder reaction of cyclohexadiene and 1,3-dioxazole

Figure 5: Reaction scheme for the Diels-Alder reaction between 1,3-dioxole and cyclohexa-1,3-diene

MOs

For this exercise, the endo and exo reaction pathways of the Diels-Alder reaction between 1,3-dixole and cyclohexa-1,3-diene where investigated. The method employed was to first build and optimise the structures of the products and then break the two C-C bonds which formed during the reaction and freeze them at a distance of 2.2 Å, to give the exo and endo guess TS. These guess TSs where then minimised before being optimised to give the final optimised TS. In this exercise, all minimisation and TS optimisations where first preformed using PM6 method, and then using the result optimised at B3LYP level. The IRC calculations where performed at the PM6 level using the PM6 optimised TS as the input, as the corresponding IRC calculations at the B3LYP level have a significantly long run time.

Figure 6: MO diagram of the endo transition state

Figure 7: MO diagam of the exo transition state

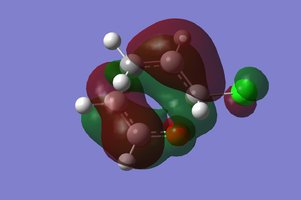
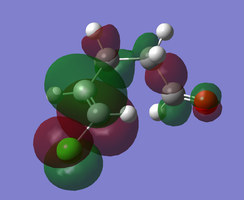
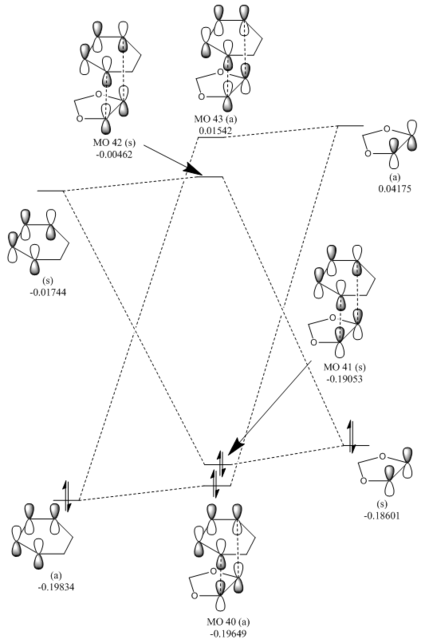
The MO diagrams for the endo (figure 6) and exo (figure 7) TSs is broadly similar to the MO diagram for exercise 1, with the TS orbitals being higher in energy relative to the reactant MO levels. In a normal electron demand process the diene HOMO is higher in energy than the dienophile HOMO, and the diene HOMO-dienophile LUMO energy gap is smaller compared to the converse dienophile HOMO-diene LUMO energy gap. However, in this reaction the HOMO of the 1,3-dioxole (dienophile) is higher in energy than the cyclohexa-1,3-diene (diene) HOMO, and this means that the reaction is an inverse electron demand Diels-Alder. This is because the dienophile is relatively electron rich, as the oxygen atom substituents can donate electron density (via lone pairs in valence p orbitals) in to the alkene π bond, thus raising the orbital energy levels of the dienophile. Again, this reaction obeys the principle of orbital symmetry.

Nf710 (talk) 10:56, 6 March 2018 (UTC) What you have said is theoretically correct but you could have backed up this discussion by investigating the relative ordering of the MOS by doing a single point calc of the reactants.

Additionally it is noticeable that the energy levels of the endo and exo transition state are different. For example the TS HOMO (MO41) for the endo TS is lower in energy than that of the exo transition state. This result is to be expected since the exo TS is higher in energy than the endo, as the endo TS has stabilising secondary orbital interactions.

The secondary orbital interaction in the endo TS can be seen when viewing the TS MOs (see figure 8), as in addition to the main frontier MO interactions, the oxygen p-orbitals interact with the back of the π-orbitals of the diene component, which provides an additional stabilising factor. This lowers the reaction barrier for the reaction, relative the reaction forming the exo product.

Reactants

HOMO of Cyclohexadiene

HOMO of 1,3-Dioxole

LUMO of Cyclohexadiene

LUMO of 1,3-Dioxole

Endo Transition-State

ENDO-TS HOMO

ENDO-TS LUMO

ENDO-TS HOMO - 1

ENDO-TS LUMO + 1

Exo Transition State

EXO-TS HOMO

EXO-TS LUMO

EXO-TS HOMO - 1

EXO-TS LUMO + 1

Thermochemistry

Species	Sum of electronic and thermal free energies (Hartee/particle)
1,3-Dioxole	-233.321
Cyclohexa-1,3-diene	-267.068
Endo Transition State	-500.332
Exo transition state	-500.329
Endo product	-500.419
Exo product	-500.417

Reaction product	Reaction Barrier (KJ / mol)	Reaction Energy (KJ/mol)
Endo	151.04	-76.18
Exo	158.86	-72.59

The thermochemistry section form the log file output of optimisation calculations contained the sum of electronic and thermal free energies which where subsequently used to determine the reaction barriers and reaction energies. The values for the reaction barriers and reaction energies for both the endo and exo reaction pathways are summarised in the above table. The results reveal that the endo reaction has a lower reaction barrier and a larger reaction energy (i.e. the endo product is lower in energy), compared to the exo reaction, thus the endo product is both the kinetic and thermodynamic product. The smaller activation energy for the formation of the endo product is due to the presence of stabilising secondary orbital interactions in the endo TS (which are absent in the exo TS), which means the product is kinetically favoured, . The endo product is the more stable product because it is less sterically encumbered than the exo. This because even though the exo product has the newly formed C-C in an equatorial position, they are in relatively close proximity to the CH2-CH2 bridge which results in steric clashes with the fused 5 membered ring (originating from the 1,3-dioxole). In the endo product, the 5-membered ring is in close proximity to a CH=CH bridge, and therefore experience less steric repulsion, making the more stable thermodynamically favoured product (see figure 9). Also, the greater steric repulsion may be an additional factor for the higher activation energy required for the exo relative to the endo Diels-Alder reaction.

Figure 8: MO41 of the endo transition state, displaying secondary orbital interactions

Figure 9: Structue of exo and endo prodcut

Endo product

Exo product

Nf710 (talk) 11:05, 6 March 2018 (UTC) This was a good section, There were some part where you could have gone into more detail. Your discussion of of the SOO and sterics was particular good. You could have spoke in more detail about the kinetics. Also your energies are slightly out. I belive this is becuase you have miss calculated your reactant energies.

LOG files

Optimised 1,3-Dioxole = File:AS6115DIOXAZOLE MIN B3LYP.LOG

Optimised cyclohexa-1,3-diene = File:AS6115CYCLOHEXADIENE MIN B3LYP.LOG

MO energy levels of reactants = File:AS6115REACTANTS ENERGY.LOG

Optimised Endo TS = File:AS6115ENDO TS OPT B3LYP.LOG

Optimised Exo TS = File:AS6115EXO TS OPT B3LYP.LOG

Optimised Endo product = File:AS6115ENDO PRODUCT MIN B3LYP.LOG

Optimised Exo product = File:AS6115EXO PRODUCT MIN B3LYP.LOG

Excercise 3:o-xylylene sulfur dioxide cycloadditions: Diels-Alder v. Cheletropic

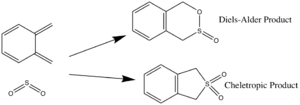
Figure 10: Reaction Scheme for the different possible cycloaddition reactions between SO2 and the exocyclic diene unit of o-xylylene

For this experiment the TSs of different possible pericyclic (figure 10) reactions were located and optimised at the PM6 level. The method used to obtain the TS was to firs build and optimise the products of each of these reactions, individually, then break and freeze the bonds which form as a result of the cycloaddition in order to generate a relatively accurate guess TS. From the optimised TSs the IRC calculations.

From the output (log files) of the optimisation calculation the free energy values for the reactants, products and TSs were collated and used to determine the reaction barriers and energies for each reaction pathway (see tables below).

Thermochemistry

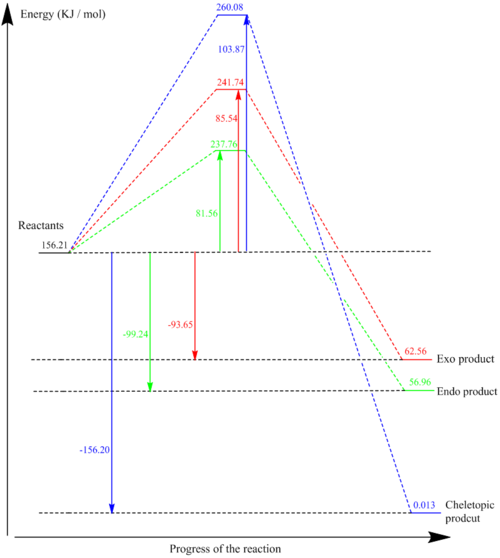
The reaction profile (figure 11) illustrates the data shown in the tables below. The endo product is the kinetic product ads it has the lowest reaction barrier; this is primarily due to stabilising secondary orbital interactions in the endo TS. Also the endo product has a slightly larger reaction energy than the exo product, indicating the endo product is more thermodynamically favourable than the exo. The cheletropic reaction has the highest activation energy of the pathways but also has the highest reaction energy, which means that the cheletropic product is the less kinetically favourable but more thermodynamically favourable than either the endo or exo Diels-Alder. The cheletropic reaction has the highest activation energy because the cheletropic TS is much higher in energy than the endo or exo Diels-Alder TS. This difference can be attributed to the fact that in the cheletropiuc reaction the TS involves forming a 5-membered ring which is more strained and therefore less stable than the 6-membered chair-like TS for the Diels-Alder reactions. S=O bonds are relatively strong and therefore the fact that the cheletropic reaction has two S=O bonds means it is lower in energy compared to the endo and exo products of the Diels-Alder reaction in which one of the two S=O bonds are broken. This explains why the cheletopic reaction is the thermodynamically favoured product.

Species	Sum of thermal and electronic free energies (Hartee/Particle)
Sulfur dioxide	-0.118614
o-Xylylene	0.178112
Endo Transition State	0.090562
Exo Transition state	0.092078
Cheletopic Transition State	0.099062
Endo Product	0.021697
Exo Product	0.023829
Cheletropic reaction	0.000005

(Your exo product hasn't fully converged to a minimum. You need to check your geometries for imaginary frequencies Tam10 (talk) 10:26, 6 March 2018 (UTC))

Reaction Product	Reaction Barrier (KJ/mol)	Reaction energy (KJ/mol)
Endo	81.56	-99.24
Exo	85.54	-93.65
Cheletrophic	103.87	-156.20

As a result of the Diels-Alder and Cheltropic reaction the 6-membered ring of the xylylene reactant is converted into an aromatic benzene ring. The aromatisation of the xylylene ring is a thermodynamic major driving force for these reactions, which explains why the o-xylylene is relatively unstable, as it is readily converted to an aromatic product, as demonstrated by the IRC animations below.

IRC Paths

Endo pathway	Exo pathway	Cheletrophic
IRC animation	IRC animation	IRC animation

Alternative Diels-Alder reaction

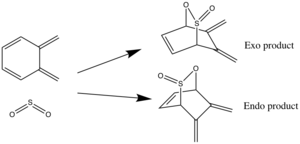
Figure 12: Reaction Scheme showing the exo and endo products of the Diels Alder reaction between sulphur dioxide and the diene unit with the 6-membered ring of o-xylylene

In addition to the exocyclic diene unit utilised for the Cheletropic and Diels-Alder reactions describe above, there is a second s-cis diene unit with the xylylene ring which can undergo a Diels-Alder reaction (figure 12) with sulphur dioxide. The same procedure used to locate was used to locate the TS for the endo and exo pathway for this alternative Diels-Alder reaction, and the subsequent energetic analysis, summarised in the tables below.

Species	Sum of thermal and electronic free energies (Hartee/Particle)
Sulfur dioxide	-0.118614
o-Xylylene	0.178112
Endo Transition State	0.090562
Exo Transition state	0.092078

Reaction Product	Reaction Barrier (KJ/mol)	Reaction energy (KJ/mol)
Alternative Endo	108.09	16.04
Alternative Exo	119.61	20.50

The data shows that this alternative Diels-Alder reaction is kinetically and thermodynamically unflavoured. Both the endo and exo TSs are higher in energy than the TSs for the cheletropic and Diels-Alder reactions, with the exocyclic diene of Xylylene. The reaction barriers for the alternative Diels-Alder reaction are very high as the approach trajectory of the sulfur dioxide to the cis-diene within the xylylene ring is sterically hindered, compared to the exocyclic diene which is more sterically accessible. Also the reaction is thermodynamically unfavourable as the reaction energies are positive (both exo and endo pathways are endothermic). This is because this Diels-Alder reaction doesn’t benefit from the aromatisation of the o-xylylene ring.

LOG files

Optimised sulfur dioxide = File:AS6115SO2 MIN.LOG

Optimised o-xylylene = File:As6115O-XYLYLENE MIN.LOG

Optimised endo TS = File:AS6115ENDO TS OPT.LOG

Optimised exo TS = File:AS6115EXO TS OPT.LOG

Optimised Cheletropic TS = File:AS6115CHELETROPHIC REACTION TS OPT.LOG

Optimised endo Product = File:AS6115ENDO PRODUCT MIN PM6.LOG

Optimised exo Product = File:AS6115EXO PRODUCT MIN.LOG

Optimised Cheletropic Product = File:AS6115CHELETROPIC PRODUCT MIN.LOG

Alternative Diels-Alder exo TS = File:AS6115ALT-DA EXO TS OPT.LOG

Alternative Diels-Alder endo TS = File:AS6115ALT-DA ENDO TS OPT.LOG

Alternative Diels-Alder exo product = File:AS6115ALT-DA EXO PRODUCT MIN.LOG

Alternative Diels-Alder endo product = File:AS6115ALT-DA ENDO PRODUCT MIN.LOG

Extensions

Electrolytic ring opening/closure

Figure 13: Reaction scheme for the electrocylic ring closing/opening reaction between 3,4-dichlorocyclobut-1-ene and (2Z,4E)-2,5-dichlorohexa-2,4-diene

The 4π-electrocyclic ring opening/closing reaction which interconverts 3,4-dichlorocyclobut-1-ene and (2Z,4E)-2,5-dichlorohexa-2,4-diene was investigated. The ring open form was first built in Gaussian and minimised, and then the carbon atoms between which the bond forms during the ring closing reaction had their coordinates frozen. This guess-TS was then optimised at the PM6 level. From this an IRC calculation was run (animation shown below). The same analysis of reaction barriers and reaction energy as done in exercises 1 and 2 was performed from this reaction. (Please note that the activation energy and reaction energy quoted in the table is specifically for the ring-opening electrocyclic reaction.)

IRC animation
Figure 14 Animation the elctrocyclic ring closing reaction

As expected the ring open diene form is more stable than the cyclobutene. This is two be expected as the 4-membered ring is highly strained (it suffers from significant angle strain and torsional strain). Also the high torsional strain means that the two chlorine substituents are locked in the cis conformation and therefore the molecule also suffers from steric strain since the chlorine atoms are relatively large.

(It could be worth investigating the trans- butene to see how much sterics affects the reaction energy Tam10 (talk) 10:48, 6 March 2018 (UTC))

Species	Sum of thermal and electronic free energies (KJ/mol)
(2Z,4E)-2,5-dichlorohexa-2,4-diene	129.8514108
Transition State	326.2969913
3,4-dichlorocyclobut-1-ene	177.5923287

Reaction Barrier (KJ / mol)	Reaction Energy (KJ/mol)
148.70	-47.74

The reaction energy is negative which indicates that the electrocyclic ring opening is exothermic and therefore thermodynamically favourable. This is to be expeected since the ring opening process relieves the ring strain and forms the less sterically strained diene product in which the chlorine atoms are further apart.

From analysis of the stereochemistry of the products and reactants form the IRC, it can be stated that this electrocyclic reaction is conrotation (i.e. the two chlorine substituents will rotate in the same direction during the reaction). This can be explained by considering the Woodward-Hoffman rules. The Woodward-Hoffman rules is based on the principle of conservation of orbital symmetry, and states that for a thermally allowed pericyclic reaction the number of components with the correct number of which satisfy: (4q +2)s + (4r)a must be odd. Where q and r are integers and the susbscript s represents suprafacially interacting components and a represents antrafacial components. For this electrocyclic reaction can be considered as being a single component with four π-electrons and as such this means it must interact antarafacially for this reaction to be thermally allowed (see figure 15). This antrafacial interaction can only be achieved via a conrotatory mechanism. Figure 15 shows how the it is necessary for the HOMO of the diene to undergo conrotation in order for to overlap in such a fashion to form the new C-C σ bonding orbital, in the cyclobutene product.

Figure 15: Schematic illustrating the conrotatory ring closing mechanism

The frontier MOs for the reactant, TS and product for this electrocyclic reaction are displayed in the table below. The HOMO and LUMO of 2,5-dichlorohexa-2,4-diene are similar to that of butadiene, allbeit with additional contribution from the chlorine atoms. Comparing the HOMO of 2,5-dichlorohexa-2,4-diene to the HOMO of the TS, seems to support the Woodward-Hoffman analysis that this reaction proceeds with conrotation. However the frontier MOs of the TS and 3,4-dichlorocyclobut-1-ene are quite complicated which makes analysis difficult. When looking at the energies it can be seen that the HOMO of the TS is higher in energy than that of the reactant and products, which is to be expected since the TS is the highest energy point in the IRC, however the opposite trend is observed for the LUMOs.

Species	HOMO	LUMO
(2Z,4E)-2,5-dichlorohexa-2,4-diene	IRC animation Relative Energy: -0.3574	IRC animation Relative Energy: -0.01145
Transition State	IRC animation Relative Energy: -0.33726	IRC animation Relative Energy: -0.02386
3,4-dichlorocyclobut-1-ene	IRC animation Relative Energy: -0.38986	IRC animation Relative Energy: -0.00382

(You are showing the conversion of 4 pi orbitals to 2 pi and 2 sigma orbitals, and so 4 MOs are needed for the analysis. It looks like the HOMO of the products might not be so relevant to this Tam10 (talk) 10:48, 6 March 2018 (UTC))

LOG files

Optimised (2Z,4E)-2,5-dichlorohexa-2,4-diene = File:AS6115EXT1-RING-OPEN-MIN.LOG

Optimised Transition state = File:As6115-Ext1CORRECT-TS-OPT.LOG

Optimised 3,4-dichlorocyclobut-1-ene = File:AS6115CORRECT(2Z4E)-25-DICHLOROHEXA-24-DIENE-MIN.LOG

Claisen Sigmatropic rearrangement

Figure 16: Reaction Scheme of the Claisen rearrangement between 3-chloro-3-(vinyloxy)prop-1-ene and (E)-5-chloropent-4-enal

The claisen rearrangement is a [3,3]-sigmatropic rearrangement reaction which converts 3-chloro-3-(vinyloxy)prop-1-ene to (E)-5-chloropent-4-enal was also investigated in this experiment. The method used the TS was to directly carry out a TS (Berny) optimisation of a guess-TS for the sigmatropic reaction (a chair-like structure) at the PM6 level. Following this an IRC calculation was run. From the initial and final frame of the IRC reactant and product of the Claisen (i.e. the allyl vinyl ether and unsaturated aldehyde) was obtained and optimised.

IRC animation
Figure 17 Claisen rearrangement IRC

Species	Sum of thermal and electronic free energies (KJ/mol)
3-chloro-3-(vinyloxy)prop-1-ene	82.12887106
Transition State	222.5397832
(E)-5-chloropent-4-enal	33.55569021

Reaction Barrier (KJ / mol)	Reaction Energy (KJ/mol)
140.41	-48.57

The data in the tables above reveal that the aldehyde product is more stable than the allyl vinyl ether. This is essentially due to the fact that the C=O bond is stronger than the C=C bond. (Please note the values for the reaction barrier and reaction energy are for the sigmatropic rearrangement going from the 3-chloro-3-(vinyloxy)prop-1-ene to the (E)-5-chloropent-4-enal). The reaction is exothermic, as the reaction energy is negative, and as it is thermodynamically favourable to form the aldehyde product.

The alkene in the aldehyde product has E-stereochemistry this can be explained from the analysis of the Claisen TS. The transition state has a chair like structure and the large chlorine substituent prefers to adopt a pseudo-equatorial position, and therefore proceeds to form the E-alkene product (see figure 17).

Species	HOMO	LUMO
3-chloro-3-(vinyloxy)prop-1-ene	IRC animation Relative Energy: -0.36103	IRC animation Relative Energy: -0.00247
Transition State	IRC animation Relative Energy: -0.31763	IRC animation Relative Energy: -0.01767
(E)-5-chloropent-4-enal	IRC animation Relative Energy: -0.36658	IRC animation Relative Energy: -0.00822

(Again here you have 6 electrons and 6 orbitals that you'd need to track from reactants to products. There are going to be some complicated rotations going on converting sigma and pi orbitals at the reacting sites Tam10 (talk) 10:48, 6 March 2018 (UTC))

The frontier MOs of the reactant, TS and product for this claisen rearrangement along with their corresponding relative energies are listed in the table above. The MOs for this system are quite complex and it is difficult to discern how the frontier MOs develop on going from the allyl vinyl ether through the TS to the γ,δ-unsaturated aldehyde. When considering the relative energies of the frontier MOs the trend observed, is the same as that of the electrocyclic reaction, with the TS HOMO being higher in energy than the reactant and product HOMOs, whilst the TS LUMO is lower in energy than the LUMO of the reactant and product.

LOG files

Optimised 3-chloro-3-(vinyloxy)prop-1-ene = File:AS6115VINYL-ALLYL-ETHER-MIN.LOG

Optimised (E)-5-chloropent-4-enal = File:AS6115UNSATURATED-ALDEHYDE-MIN.LOG

Optimised TS = File:AS6115CLAISEN3-GUESS TS.LOG

Conclusion

Overall this experiment used relatively complex computational techniques on Gaussian to locate the TS structures for a variety of different pericyclic reactions, as well as reveal more information about the reactions. In exercise 1 a simple Diels-Alder reaction was investigated and the MOs of the TS and reactants were explored.

In exercise 2 the endo and exo reaction pathways of an inverse electron-demand Diels-Alder was studied and again the frontier MOs of the system were considered. Also reaction barriers and reaction energies where calculated, which revealed the endo product was both the kinetic and thermodynamic product of the reaction.

In exercise 3, a range of different possible cycloaddition reactions which can take place between o-xylene and sulfur dioxide where considered and compared, in terms of activation energies and reaction energies to probe how thermodynamically and kinetically favoured each pathway is.

In addition, further work was carried out to investigate applications of these techniques to other pericyclic reactions. This included the elucidation that the electrocyclic ring opening/closing reaction was conrotatory, in accordance with the Woodward-Hoffman rules. Furthermore, an evaluation of a [3,3]-sigmatropic rearrangement TS helped reveal the stereoselectivity of the reaction.

Ultimately, the confidence that can be placed in the findings of this experiment is limited by the accuracy of the computational methods used. The experiment could be improved by using more accurate methods (e.g repeating optimisation calculations for excercises 1 and 3 at the B3LYP level). Additionally comparing the predictions of the in sillico model with experimental data would allow the validity of this computational experiment to be assessed.