Cope Rearrangement Tutorial

Introduction

A cope rearrangemnt is a [3,3] sigmatropic shift of a 1,5-diene. In this experiment 1,5-hexadiene was investigated using various computational methods in order to characterise the products/reactants and the transition state of the reaction.

Optimising the Reactants and Products

The first 4 calculations were all carried out at the HF/3-21G level of theory.

The first calculation carried out was an optimisation of 1,5-hexadiene. This optimisation was carried out with the hexadiene initially in the "anti" configuration (Molecule 1). The optimised structure had C₂ symmetry but wasn't significantly different from the initial structure.

The second calulation was another optimisation of 1,5-hexadiene, this time with a gauche geometry about the central 4 C atoms. The optimised structure was lower in energy than the anti structure indicating that it is more stable. It had had C₁ symmetry. This was the lowest energy conformer of 1,5-hexadiene that was found.

A third optimisation of 1,5-hexadiene was carried out starting with the central C-C-C-C in an anti-periplanar arrangement. This led to a different gauche structure that was higher in energy, and therefore less stable, than the previous gauche structure.

The final calculation done at the HF/3-21G level of theory was to obtain another conformer with an anti configuration of the central 4 C atoms. The resulting structure had a C_i point group.

The anti, C_i conformer was reoptimised at the B3LYP/6-31G* level of theory. This level finds the optimum structure to a finer level of detail, using a larger basis set, at the cost of more processing time.

The structure didn't change much under the more detailed calculation and had the same point group. The sp₂ bond angles increased by around 2 degrees.

The fully optimised structure was subjected to a frequency analysis to determine if a potential energy minimum had been reached. All the vibrational frequencies reported were real and positive indicating that the potential minimum had been reached.

298.15K
 Sum of electronic and zero-point Energies=    -234.469212
 Sum of electronic and thermal Energies=       -234.461856
 Sum of electronic and thermal Enthalpies=     -234.460912
 Sum of electronic and thermal Free Energies=  -234.500822

Optimising the "Chair" and "Boat" Transition Structures

Having optimised the structures of the products and reactants, the transition structures were optimised. This is a more difficult because transition structures are not potential energy minima but are saddle points, with a negative potential energy gradient along a single coordinate. Therefore different techniques are required in order to obtain the correct structures.

"Chair" Transition State

The first calculation carried out was an optimisation of a single allyl fragment that would make up half of the final transition structure. This calculation was carried out at the HF/3-21G level of theory. The calculation was done as an optimisation to a transition state using the Berny algorithm. This method found a transition state, it's nature as a transition state rather than a potential minimum being confirmed by the presence of a single negative frequency in the vibrational spectrum at 818cm^-1. This vibrational frequency corresponded to the two allyl fragments moving into either product of the Cope rearrangement.

The second calculation was another method that can be used to obtain the transition state. In this method the atoms corresponding to the two new bonds were frozen at ~2.2Å and then a optimisation done. the bonds were then unfrozen and another optimisation to transition state performed. This method gave a structure of the transition state very similar to the first method.

298.15K
 Sum of electronic and zero-point Energies=           -234.414932
 Sum of electronic and thermal Energies=              -234.409011
 Sum of electronic and thermal Enthalpies=            -234.408067
 Sum of electronic and thermal Free Energies=         -234.443816

The chair transition structure had an electronic energy of -234.556983 hartrees under the B3LYP/6-31G* method.

"Boat" Transition state

The boat transition state was found using a different method again, the QST2 method, which moves between the reactant structure and the products structure in order to find the transition state. The boat transition structure has a slightly longer distance between the allyl fragments than in the chair conformation. this is due to additional steric repulsion between the CH₂ at each end of the boat.

298.15K
 Sum of electronic and zero-point Energies=           -234.402346
 Sum of electronic and thermal Energies=              -234.396011
 Sum of electronic and thermal Enthalpies=            -234.395067
 Sum of electronic and thermal Free Energies=         -234.431755

The boat transition structure had an electronic energy of -234.543093 hartrees under the B3LYP/6-31G* method.

Activation Energies

The activation energy of the reaction can be worked out by finding the energy difference between the reactants and products.

The energy of the reactants is -234.469212 hartrees at 0K and -234.461856 hartrees at 298K. By subtracting the energy of the transition state from that of the reactant, the activation energy (E_a) for the process can be found.

Structure	Energy of transition state (hartrees)	E_a (hartrees)	E_a (kcal/mol)
Chair 0K	-234.414932	0.05428	34.06
Boat 0K	-234.402346	0.066866	41.96
Chair 298.15K	-234.409011	0.052845	33.16
Boat 298.15K	-234.396011	0.065845	41.32

These values show that the transition state is lowered in energy at higher temperatures. This would contribute to higher reaction rates at higher temperatures. The experimental values for the chair and boat transition states at 0K are 33.5 ±0.5 kcal/mol and 44.7 ±2.0 kcal/mol respectively^[1]. These values show the same ordering as the computed values which means that the preferred transition state has been correctly identified as the chair.

Diels Alder Cycloaddition

Optimising cis-butadiene

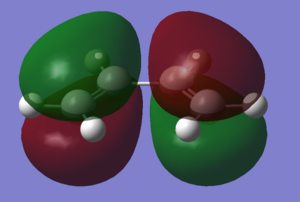
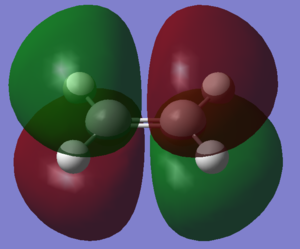
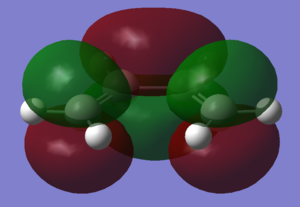
Cis-butadiene was optimised using the AM1 semi-empirical molecular orbital method. The resulting molecule was of the C_2v point group. Ethene was also optimised using the same methods to produce the above structure

The HOMO and LUMO of the two molecules are shown in the images. Relative to the plane of relective symmetry going perpendicularly through the central C-C bond the HOMO of cis-butadiene and the LUMO of ethene are anti-symmetric but the LUMO of cis-butadiene and the HOMO of ethene are symmetric. Since for two MOs to mix they must be of the same symmetry it is clear that the HOMO of cis-butadiene and the LUMO of ethene can mix together and the LUMO of cis-butadiene and the HOMO of ethene can mix together.

Optimising ethylene + cis-butadiene Transition State

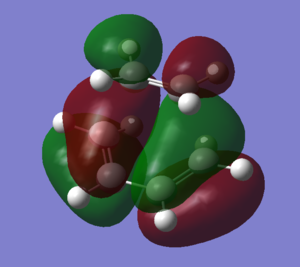
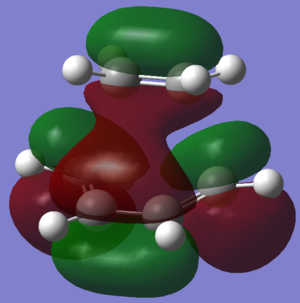
The transition state of ethylene and cis-butadiene was optimised using the AM1 semi-empirical molecular orbital method to a transition state using the Berny algorithm. The nature of the negative frequency vibration shows that the transition point is correct and corresponds to the Diels-Alder reaction as wanted. The animation of the vibration shows that the reaction is concerted and the bonds form simultaneously. There is significant bond stretching involved in the vibrational mode.

The lowest positive frequency vibration (shown on right) has a very different form to the negative vibration. The positive vibration doesn't have any bond stretching as is more energetic than bond bending which is more energetic than the vibration shown. The vibration shown actually doesn't involve any bond stertches or bends but is a twist of the whole ethene molecule relative to the butadiene. The reason it is low in energy is that it doesn't require the changing of any covalent bonds.

As with the cis-butadiene, the HOMO and LUMO of the molecule are shown in the images. Relative to the plane of relective symmetry going perpendicularly through the central C-C bond the HOMO is anti-symmetric (AS) but the LUMO is symmetric (S). Since the HOMO here is AS, as was the HOMO of the butadiene, this suggests that the butadiene HOMO is involved. The ethene LUMO is AS but is part of the HOMO for the transition state. The LUMO of the transition state is made up of the HOMO of ethene and the LUMO of the butadiene. This confirms that the MOs mix as expected.

The reaction is allowed because there are 6 (which fits the 4n+2 rule) electrons involved in the reaction and there is suprafacial stereochemistry.

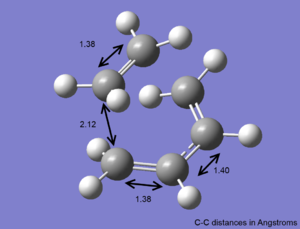
Given that an sp³ and an sp² are 153nm and 146nm respectively^[2], the intramolecular distance of 212nm is much further than a single bond. This suggests the interaction in the transition state is not covalent. The van der Waals radius of carbon is 170pm^[3]. Therefore although the internuclear bond distance is outside that observed in covalently bonded carbon atoms, it is within twice the van der Waals radius and so there is likely to be significant orbital overlap between the two carbon atoms. The interaction being observed in this transition state is more likely to be a van der Waals type interaction.

Optimising cyclohexa-1,3-diene + maleic anhydride Transition State

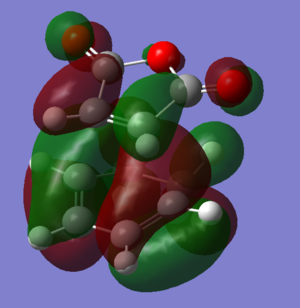
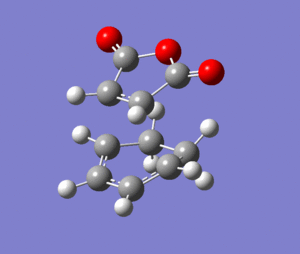
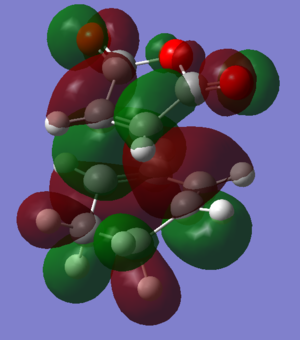
To find the transition state of this reaction the AM1 forcefield was initially used to optimise the molecules to a transition state and then the B3LYP/6-31G* level of theory used on the pre-optimised structures. The files used in the final calculations can be found by clicking on the following two links: [Endo D-Space] [Exo D-Space]

The relative energies are -612.68339675 hartrees for the endo form and -612.67931096 hartrees for the exo form. This shows that the endo transition state is lower in energy and so the kinetically preferred product in this reaction is the endo product.

The structures of each fragment were largely similar, one difference was that the H-C-C-O dihedral angle was 160 in the endo transition state and 157 in the exo transition state. The maleic anhydride fragment was slighlty closer to planar in the endo structure (dihedral angle of 180). this is because the exo form is more strained due to the additional steric clash between the maleic part and the hydrogen atoms on sp³ carbons. On the endo form, there is less repulsion because there is only one hydrogen on the sp² carbon atoms. This strain also accounts for the other significant difference between the two structures; the increased distance between the carbons that would form bonds in the reaction which are 2.269Å in the endo transition state and 2.290Å in the exo transition state.

The HOMOs of the two transition states can be seen by clicking these buttons: The HOMO of the exo structure has a large area within the gap between the -(C=O)-O-(C=O)- fragment and the hexyl ring of low electron density, whereas the endo structure has a lot more electron density there. This suggests that there are more favourable interactions between the orbitals in the endo structure HOMO than in the exo HOMO. Thsi contributes to the increased stability of the endo state and is the secondary orbital overlap of the diene in the HOMO with the pi orbitals on the carbons α to the double bond. While this stabilises the endo transition state, it isn't present in the exo transition state.

Activation Energies

As anestimate of the reaction energies the structures of the two reactant molecules were optimised using the same B3LYP/6-31G* level of theory.

Maleic Anhydride

 Sum of electronic and zero-point Energies=           -379.233665
 Sum of electronic and thermal Energies=              -379.228481
 Sum of electronic and thermal Enthalpies=            -379.227537
 Sum of electronic and thermal Free Energies=         -379.262738

Cyclohexadiene

 Sum of electronic and zero-point Energies=           -233.296106
 Sum of electronic and thermal Energies=              -233.290933
 Sum of electronic and thermal Enthalpies=            -233.289989
 Sum of electronic and thermal Free Energies=         -233.324356

Endo TS

 Sum of electronic and zero-point Energies=           -612.502141
 Sum of electronic and thermal Energies=              -612.491787
 Sum of electronic and thermal Enthalpies=            -612.490843
 Sum of electronic and thermal Free Energies=         -612.538329

Exo TS

 Sum of electronic and zero-point Energies=           -612.498013
 Sum of electronic and thermal Energies=              -612.487662
 Sum of electronic and thermal Enthalpies=            -612.486717
 Sum of electronic and thermal Free Energies=         -612.534265

The results of the energies of the calculations are summarised in the table below:

Temperature	Energy of maleic anhydride (hartrees)	Energy of Cyclohexadiene (hartrees)	Energy of endo transition state (hartrees)	Energy of exo transition state (hartrees)	E_a endo (hartrees)	E_a exo (hartrees)	E_a endo (kcal/mol)	E_a exo (kcal/mol)
0K	-379.233665	-233.296106	-612.502141	-612.498013	0.027630	0.031758	17.34	19.93
298.15K	-379.228481	-233.290933	-612.491787	-612.487662	0.027627	0.031752	17.34	19.92

This shows that the activation energy for the reaction is around 2.6 kcal/mol lower via the endo transition state than via the exo transition state. These values also suggest that the activation barrier is not strongly affected by an increase in the temperature.

Energy of the products

Further optimisations using the same basis sets and methods were carried out to optimise the products of the reactions to determine the most stable thermodynamic product. [Endo D-Space] [Exo D-Space]

endo product

 Sum of electronic and zero-point Energies=           -612.572070
 Sum of electronic and thermal Energies=              -612.562604
 Sum of electronic and thermal Enthalpies=            -612.561660
 Sum of electronic and thermal Free Energies=         -612.607178

exo product

 Sum of electronic and zero-point Energies=           -612.569381
 Sum of electronic and thermal Energies=              -612.559977
 Sum of electronic and thermal Enthalpies=            -612.559033
 Sum of electronic and thermal Free Energies=         -612.604283

The endo product is lower in energy and so is predicted to be both the kinetic product and the thermodynamic product of the reaction.

Further Study

These calulations of Diels-Alder reactions have all focused on symmetrical reactants. The investigation could be extended by looking at reactions where the symmetry of the reactions is broken. This would affect the interactions of the orbitals and would possibly cause a switch of the preference from endo to exo.

References

↑ Origin of the preference for the chair conformation in the Cope rearrangement. Effect of phenyl substituents on the chair and boat transition states K. J. Shea, G. J. Stoddard, W. P. England, and C. D. Haffner Journal of the American Chemical Society 1992 114 (7), 2635-2643 doi: [10.1021/ja00033a042]
↑ Tables of bond lengths determined by X-ray and neutron diffraction. Part 1. Bond lengths in organic compounds F. H. Allen, O. Kennard, D. G. Watson, L. Brammer, A. G. Orpen and R. Taylor, J. Chem. Soc., Perkin Trans. 2, 1987, S1 doi: [10.1039/P298700000S1]
↑ van der Waals Volumes and Radii, A. Bondi, The Journal of Physical Chemistry 1964 68 (3), 441-451 doi: [10.1021/j100785a001]

[1] Origin of the preference for the chair conformation in the Cope rearrangement. Effect of phenyl substituents on the chair and boat transition states K. J. Shea, G. J. Stoddard, W. P. England, and C. D. Haffner Journal of the American Chemical Society 1992 114 (7), 2635-2643 doi: [10.1021/ja00033a042]

[2] Tables of bond lengths determined by X-ray and neutron diffraction. Part 1. Bond lengths in organic compounds F. H. Allen, O. Kennard, D. G. Watson, L. Brammer, A. G. Orpen and R. Taylor, J. Chem. Soc., Perkin Trans. 2, 1987, S1 doi: [10.1039/P298700000S1]

[3] van der Waals Volumes and Radii, A. Bondi, The Journal of Physical Chemistry 1964 68 (3), 441-451 doi: [10.1021/j100785a001]

[1]

[2]

[3]