Rep:Xlt15 TS

Transition States and Reactivity

Introduction

The transition state (TS) is defined as the highest energy point (maximum) on the minimum energy path linking reactants and products whereas the reactant and product are the minimum along a reaction coordinate. They are thus a stationary point with a first derivative or a gradient of zero (2). The second derivative or the curvature (4) is negative for a TS (maximum point) whereas it is positive for the reactant and product (minimum point).

Figure 1: Equation of potential energy and its first and second derivative, vibrational frequency and reduced mass .

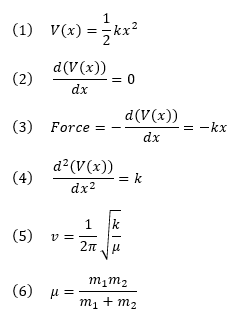
where V(x) is the potential energy, k is the force constant, x is the displacement, ν is vibrational frequency, μ is the reduced mass of 2 atoms of mass m₁ and m₂. The negative sign in (3) implying that the force acting in that direction lowers the potential energy .

Figure 2: Reaction profile of an exothermic reaction .

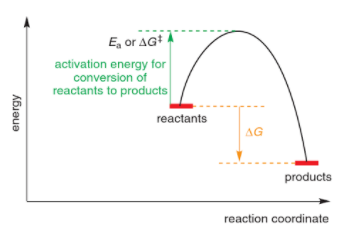
The reaction coordinate diagram provides the kinetics and thermodynamics information of a reaction. The higher the activation energy, the lower the rate of reaction. A pathway with more exothermic reaction energy is more thermodynamically favoured.

A non-linear molecule undergoing a reaction will have 3N_atoms-6 reaction coordinates . The 3N_atoms-6 specifies the number of internal degree of freedom or the number of normal vibrational mode that a molecule can possess . For a linear molecule, the number of internal degree of freedom is 3N_atoms-5 as rotation along bond axis give the identical molecule . Hence, a reaction coordinate diagram beyond 1D is called a potential energy surface. The transition state in a PES is defined as the first order saddle point on PES with the first derivatives with respect to all coordinates are 0 . The first order saddle point has a maximum energy for displacement between 2 minima in a direction whereas in all the remaining directions the energy is a minimum . Hence, the transition state has only a unique normal coordinate that corresponds to reaction coordinate with second derivative < 0 (negative force constant). This negative force constant can then be related to the vibrational frequency (5) which is an imaginary frequency. The chemical reactant and products are characterized as minima and must have second derivative > 0 (positive force constant and hence positive vibrational frequency).
Nf710 (talk) 22:27, 21 February 2018 (UTC) remeeber you must be talking about 3N-6 degrees of freedom for you minimum too. I know what you are saying. You can get your force constants from teh eigenvalues of the hessian matrix at the TS geometry. The eigen vetcors are the normal modes.
Two different electronic structure methods, the semi-empirical method PM6 and Density Functional Theory (DFT) method B3LYP were used in optimizing the reactants, transition state and product. The semi-empirical PM6 is a faster method to generate a reasonable result as it uses the experimental data whereas B3LYP is more time-consuming and accurate method . Hence, PM6 method was firstly used to generate an approximate structure and then reoptimize with DFT method B3LYP for Exercise 2.

Exercise 1: Reaction of Butadiene with Ethylene

Figure 3: Reaction scheme of Diels-Alder reaction of 1,3-butadiene and ethylene.

Diels-Alder (D-A) reaction or [4+2]-cycloaddition occur between a conjugated diene and an alkene (dienophile). The diene component must adopt a s-cis conformation. D-A reaction involved a one step, concerted formation of 2 new σ bonds. The D-A reaction proceeds with no reaction intermediates and the transition state has aromatic character with six delocalized π electron.

Method Used In Optimization and Analysis
Method 3 was employed in locating the transition state by which the product, cyclohexene was drawn and optimized to minimum at PM6 level. With the optimized cyclohexene, the C-C single bonds formed during the reaction of 1,3-butadiene and ethylene were deleted, froze at 2.20 Å and optimized to minimum at PM6 level to identify the frozen guess transition state. The distance 2.20 Å is the approximate separation between the reacting termini in guess transition state. It is a value between a C-C single bond length and their combined Van der Waals radii. The guess TS structure was then optimized at PM6 level and the PM6 optimized TS was used to run a IRC calculation. For reactants, 1,3-butadiene and ethylene, they were each obtained from the first frame of IRC calculation and optimized to minimum at PM6 level.

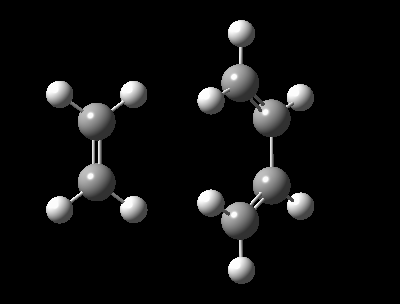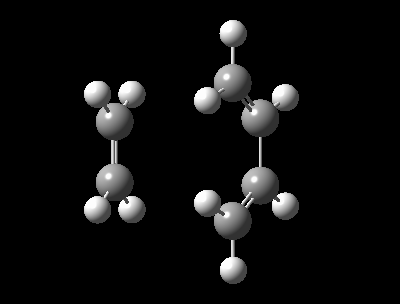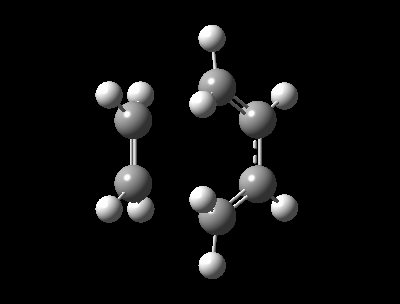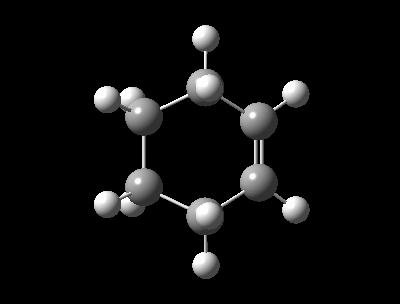
Optimized Reactants, Transition State and Product and at PM6 Level.

Table 1: Optimized Reactants, Transition State and Product at PM6 level
1,3-Butadiene	Ethylene	Transition State	Cyclohexene

Determination of The Correct TS with a Frequency and IRC Calculation

Frequency calculation

Figure 4: Screenshot of the "Display Vibrations" of transition structure.

Figure 5: Screenshot of a section of transition structure's log file.

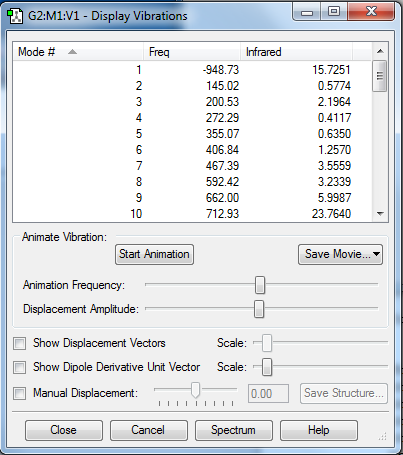
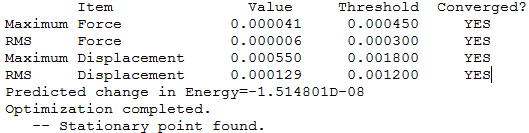
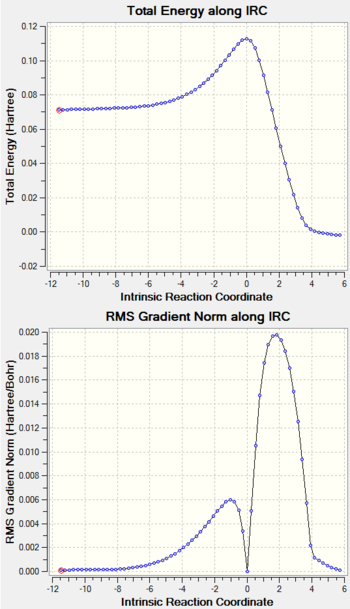
According to Figure 4 and 5, the TS structure has shown to properly converged with the presence of only one imaginary frequency at -949 cm^-1 and a stationary point corresponds to the transition structure is found. The imaginary frequency is then visualized to ensure a correct transition state structure is obtained (See Section 1.2.5 for the visualization of the imaginary frequency). For reactants (1,3-butadiene and ethylene) and product, their structures are checked to properly converge with no negative frequency obtained and their respective stationary points are found in log files.

IRC Calculation

Table 2. IRC Calculation of PM6 Optimized Transition Structures
Reaction Progress	IRC Output	Explanation
		An IRC (Intrinsic reaction coordinate) calculation is obtained for the PM6 optimized transition state structure. The plot of total energy against IRC is asymmetric and all the gradients for reactants, product and transition state (minima) are zero, indicating that it is properly converged and optimized.

MO Analysis

(Fv611 (talk) Your analysis is good, but you haven't ordered the TS MOs according to their computed energies. As this is a TS MO diagram, the bonding TS MOs will be higher in energy than expected, and the antibonding ones will be lower.)

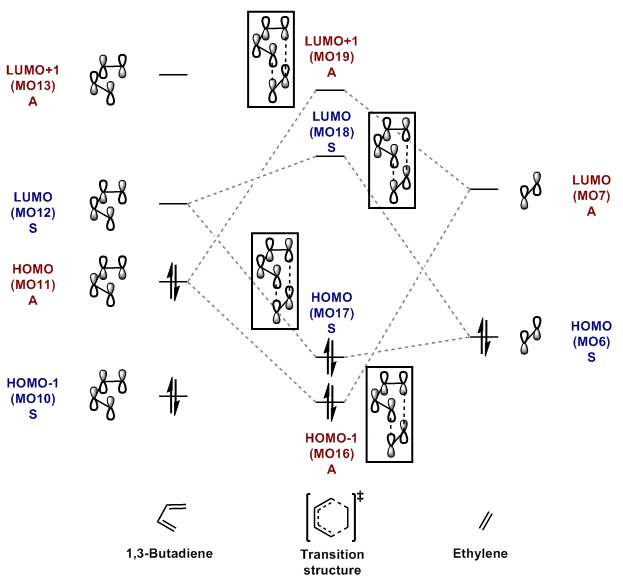
MO Diagram of The Formation of 1,3-Butadiene/Ethylene TS

Figure 6: MO diagram for the formation of the 1,3-butadiene/ethylene TS with basic symmetry labels shown; A= Antisymmetric and S= Symmetric.

HOMO: Highest Occupied Molecular Orbital
LUMO: Lowest Unoccupied Molecular Orbital

As seen in the MO diagram drawn in Figure 6, it is a normal electron demand Diels-Alder reaction because the HOMO of 1,3-butadiene (diene) is higher in energy than the HOMO of ethylene (dienophile). The combination of the high energy HOMO (diene) and low energy LUMO of dienophile gives a better overlap in the transition state. As their energy gap is smaller, it is more favoured than the interaction between LUMO of 1,3-butadiene and HOMO of ethylene (larger energy gap and hence worse overlap).

Frontier MO of Reactants and Transition State

Table 3: Frontier MO of 1,3-Butadiene, Ethylene and Transition State.
1,3-Butadiene	Ethylene	Transition State	Orbital Interaction and Discussion
LUMO, MO12, S	HOMO, MO6, S	HOMO, MO17, S LUMO, MO18, S	“+” stands for an in-phase combination and “-” stands for an out-of-phase interaction 1,3-Butadiene (LUMO, MO12, S) + Ethylene (HOMO, MO6, S) = TS (HOMO, MO17, S) 1,3-Butadiene (LUMO, MO12, S) - Ethylene (HOMO, MO6, S) = TS (LUMO, MO18, S) MO17: Although the orbital lobes on the reacting C termini of 1,3-butadiene is not observed but there is an increased in the size of the blue lobe of ethylene MO6, implying a bonding interaction between the two. MO18: The ethylene MO6 has diminished; Antibonding interaction.
HOMO, MO11, A	LUMO, MO7, A	HOMO-1, MO16, A LUMO+1, MO19, A	“+” stands for an in-phase combination and “-” stands for an out-of-phase interaction 1,3-Butadiene (HOMO, MO11, A) + Ethylene (LUMO, MO7, A) = TS (HOMO-1, MO16, A) 1,3-Butadiene (HOMO, MO11, A) - Ethylene (LUMO, MO7, A) = TS (LUMO+1, MO19, A) MO16: A very clear bonding interaction can be observed. MO19: Again, the orbital lobes are not observed for the reacting termini in 1,3-butadiene; Antibonding interaction.

Table 4: Summary of orbital overlap integral.
Interaction Type	Orbital Overlap Integral
Symmetric-symmetric	Non-zero
Antisymmetric-antisymmetric	Non-zero
Symmetric-antisymmetric	Zero

The Table 4 above summarizes the overlap integral for three different interactions. Each transition state MO is designated as symmetric (S) or antisymmetric (A) with respect to the persistent symmetry element, a mirror plane perpendicular to the central C-C bond in 1,3-butadiene. According to conservation of orbital symmetry, the orbital symmetry of reactants is smoothly transformed to an orbital of product with the same symmetry . Thus, this symmetry will certainly persist in transition state. In addition, the frontier molecular orbital (FMO) theory states that a reaction is only allowed if there is favourable mixing between HOMO and LUMO of the reactants . By referring to the MO diagram in Figure 6, the HOMO of 1,3-butadiene is of the same symmetry as the LUMO of ethylene and the vice versa. Both interactions are thus allowed because of the matching in phases. In conclusion, only orbitals of the same symmetry in reactants can combine to form the TS molecular orbitals with the same symmetry to have a significant overlap of the combining orbitals. Fragment orbitals of different symmetry combine to give zero overlap integral and thus no bond formation.

According to Woodward Hoffmann rules, the total number of (4q+2)_s and (4r)_a components must be odd in an allowed thermal pericyclic reaction. The suffix “s” stands for suprafacial and “a” stands for antarafacial. A suprafacial component forms new bonds at the same face at both ends. An antarafacial component forms new bonds on opposite faces at both ends . The thermal pericyclic reaction is forbidden if the number is even. However, a thermally forbidden pericyclic reaction is photochemically allowed. Using the Woodward Hoffmann rules, [_π4_s + _π2_s]-cycloaddition is thermally allowed as there is one (4q+2)_s component (the ethylene) and no (4r)_a component.

C-C Bond Length Measurements and Analysis

Typical C-C Bond Length

Table 5: Typical C-C bond lengths.
Bond Type	Bond Length/ Å
C–C sp3 C–sp3 C sp3 C–sp2 C sp2 C–sp2 C	1.54 1.50 1.48
C=C sp2 C–sp2 C	1.34

C-C Bond Length Measurements

Figure 7: Reaction scheme with the all carbons numbered.

Table 6: C-C bond length measurements in reactants, transition state and product.
Molecule	Bond Length/ Å
	C1-C2	C2-C3	C3-C4	C4-C5	C5-C6	C1-C6
1,3-Butadiene	–	–	1.33344	1.47077	1.33342	–
Ethylene	1.32731	–	–	–	–	–
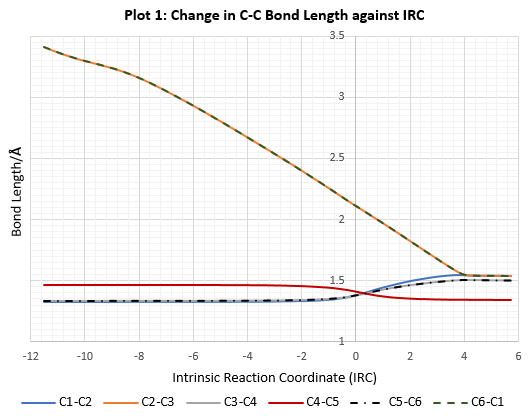
Transition State	1.38173	2.11470	1.37976	1.41112	1.37973	2.11478
Cyclohexene	1.53767	1.53577	1.49262	1.33305	1.49263	1.53577

The C-C bond length measurement with the PM6 level optimized structures is in good accordance to the typical C-C and C=C bond length. There are 2 factors affecting the bond lengths:
(a) Bond order: The higher the bond order of a given bond, the shorter the bond length and hence the stronger the bond.
(b) Type of Hybridization: The size of hybrid orbitals increases in the order of sp C > sp² C > sp³ C. The larger valence orbitals of sp³ C has poorer overlap, forming a longer and weaker bond. The percentage of s-character in hybrid orbitals decreases in the order of sp C (50%) > sp² C (33%) > sp³ C (25%). The higher the s-character of a given hybrid orbital, the shorter the bond. Because the electron in high s-character hybrid orbital can penetrate better into the nucleus and experience a higher effective nuclear attraction, resulting in a shorter bond.

Atomic Van der Waals radius of C atom: 1.70 Å
Van der Waals distance between 2 C atom: 3.40 Å

Van der Waals distance between any 2 atoms is the minimum distance beyond which the electrostatic attractive force turn into repulsive force. The length of partially formed C–C bonds in transition state is 2.11 Å, which is smaller than the Van der Waals radii between 2 C atoms but is greater than the typical C-C bond lengths listed in Table 5. This indicates the 2p atomic orbitals of C atom are partially overlap in transition state, resulting in the partly formed C-C single bond. The bond length of a partially formed or broken C=C double bond in transition state has a value between a full C-C single and C=C double bond.

Table 7: Change in C-C bond length during Diels-Alder reaction.
Bond Length against Reaction Coordinate	Explanation
	C1-C2, C3-C4, and C5-C6 All the plots show the bond length change when a C=C double bond breaks (in 1,3-butadiene and ethylene) into a C-C single bond (in cyclohexene). C=C bond length remains constant at 1.33 Å for a certain period of time. Then, the transition of transition state to product shows a gradual increase in bond length to 1.54 Å for C1-C2 and 1.49 Å for C3-C4 and C5-C6. The slight difference in C-C single bond length in cyclohexene is due to the difference in the hybridization type of C atom. C2-C3 and C6-C1 All the plots show change in bond length during the C-C single bond formation. The initial separation of terminal Cs between the 1,3-butadiene and ethylene is at 3.40 Å which is the VDW distance between 2 C atoms. As the reaction proceeds, their separation decreases almost linearly along the IRC and then it remains constant at 1.54 Å (single C-C bond formed). C4-C5 The plot shows the change in bond length when a C-C single bond (in 1,3-butadiene) forms a C=C double bond (in cyclohexene). C-C bond length remains constant at 1.47 Å for a certain period of time. Then, the transition of transition state to product shows a gradual decrease in bond length to 1.33 Å (C=C double bond formed).

Vibration That Corresponds to The Reaction Path at The Transition State

As shown in vibration mode of the imaginary vibrational frequency at -949 cm^-1, the formation of the two C-C single bonds are clearly synchronous as they are formed simultaneously. Thus, the [4+2]-cycloaddition of 1,3-butadiene and ethylene is concerted and stereospecific. In addition, this is supported by the fact the C-C bond distance of the reacting termini are the same in the transition state at 2.11 Å. Also, both 1,3-butadiene and ethylene are symmetrical and so it is expected that one C-C bond will not formed faster than the other.

Log File For IRC Calculation

IRC calculation of PM6 optimised TS: File:XLT15 IRCTS1.LOG

Exercise 2

http://wiki.ch.ic.ac.uk/wiki/index.php?title=Xlt15_Ex2

Exercise 3

https://wiki.ch.ic.ac.uk/wiki/index.php?title=Xlt15_Ex3

Further Work

https://wiki.ch.ic.ac.uk/wiki/index.php?title=Xlt15_FURTHER