Rep:Xizi

Introduction

Transition State

Transition state on a 1D potential energy surface is the highest point. But a 2D PES is in 3D-6 dimensions (degrees of freedom). It has lots of local minimas and maximas. Reactants and products corrsponding to local minimas, stationary point, with dV/dq=0 for all q and d2V/dq2>0 for all q, q is the geometric parameter. Intrinsic reaction coordinate, the lowest energy pathway linking two minima, is the path that would be followed by a molecule in going from one minimum to another when it just get enough energy to overcome the activation barrier, pass through the transition state, and reach the other minimum. A transition it is located on the maxima of the reaction path, which corresponding to reaction corrdinate, but minima of all other demesions, defined by dV/dq=0 and d2V/dq2>0 when q= reaction coordinate but d2V/dq2<0 for all other q. The geometric parameter corresponding to the reaction coordinate is usually a composite of several parameters like bond lengths, angles and dihedrals. This will result in that sometimes trasntion state can be maxima on more than one reaction coordinate, which could be called a hilltop. Because two reaction path will lead to the same transition state, like the first exercise in the extension work. (1)

Nf710 (talk) 22:58, 8 February 2018 (UTC) q at the transition state is in the basis of the normal modes which is a linear combination of all bond rotations, streches and bends. and hnce looks like a vibration.

Born–Oppenheimer Approximation

When talking about the geometric coordiante, it is defined by nuclear coordinates the parameter. Which is to say, a potential energy surface is a plot of the energy of a collection of nuclei and electrons against the geometric coordinates of the nuclei. The reason is in the BO approximation which say nuclei could be assumed stationary with respect to electrons. So Schrcodinger equation for a molecule could be separated into an electronic and a nuclear equation. Two solved and added together to get the total internal energy.

Computational method

Computational method finds potential energy by computing Haltonian <Ψ|H|Ψ>=E, direction vectors, r=ax+by+cz=(1,3)Σci|i> in 3D space.
LCAO gives |Ψ>=(1,N)Σci|Φ> in N dimension. Then E=(c1,...)(<Φ1|H|Φ1>...)(c1,...) and |Φ1>=aexp(-ar2)
There are two methods used in this computational lab, semi-empirical paramazation method 6 (PM6) and density functional method Becke-3-LYP (B3lYP) with basis set 631G.
PM6 is under Hartree–Fock formalism, but make many approximations and obtain some parameters from empirical data which allows some electron correlations.
631g is a basis set of basis functions represent the electronic wave function in the Hartree–Fock method or DFT in order to turn the partial differential equations of the model into algebraic equations for computer. Molecular orbitals could then be expressed as linear combinations of the basis functions.
Becke-3-LYP: a hybrid functional uses a mixing scheme of 3 parameters
EXC = 0.2*EX(HF) + 0.8*EX(LSDA) + 0.72*DEX(B88) + 0.81*EC(LYP) + 0.19*EC(VWN)

Geometry Optimization

Geometry optimization is the process of starting with an input structure and finding a stationary point on the PES. The stationary point found will normally be the one closest to the input structure. If calculating TS, analytical first and section derivative should as algorithms to be used.

Frequency calculation and zero point energy

Calculating vibrational spectrum (normal-mode vibrations) is often needed to check if the geometry is the desired one. The algorithm for this works by calculating an accurate Hessian (force constant matrix) and diagonalizing it to give a matrix with the direction vectors,ř, of the normal modes, and a diagonal matrix with the force constants,k, of these modes. Mass weighted force constants give the normal-mode vibration frequencies, v=h/2πc* (k/m)1/2. A transition state has one imaginary vibration, corresponding to motion along the reaction coordinate. K values calculated for transition state is all positive except one on reaction coordinate.
The equations used for computing thermochemical data in Gaussian are equivalent to those in thermodynamics. One of the most important approximations to be aware of throughout this analysis is that all the equations assume non-interacting particles and therefore apply only to an ideal gas. This added up contribution of translation, electronic, vibrational and rotational motion.
Sum of electronic and thermal free energies = ɛ0 + Gcorr

Nf710 (talk) 23:03, 8 February 2018 (UTC) Nice section, you could have made the equations ab it more clear by using the wiki formatting.

Exercise 1: Reaction of Butadiene with Ethylene

MO Constructions and Data Presenting

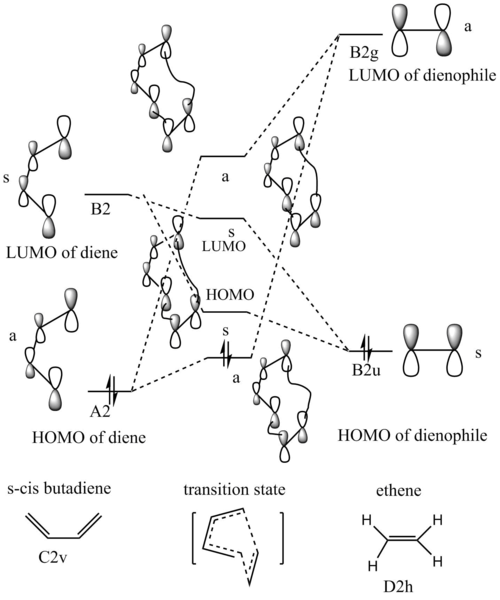
MO and FMO anlysis

table 1: table of correlations of the visualised MOs and MO diagrams in MO analysis (fig 1)

S-cis Butadiene

Ethene

Transition state

HOMO

LUMO

HOMO

LUMO

HOMO-1

HOMO

LUMO

LUMO+1

Correlation with MO diagram (Fig1)

Bond Changes in Diels Alder Reaction

table 2: Bond Length Display
carbon atom annoted

BOND LENGTH AND BOND CHANGE

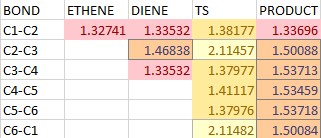
The vibration corresponds to the reaction path at transition state is shown below:

Explanation of Graph and Table and Answers to Questions

Requirements for Diels Alder Reaction

Quantitative analysis of MO with energy will be discussed in Exercise 2. In this [4+2] cycloaddition reaction, interactions were between the conjugated pi system of butadiene and pi bond of alkene to form an aromatic transition state with 6 pi electrons. Two new C-C bonds were generated between two species at ends of each. Molecular diagram for the formation of transition state was tried to be constructed. HOMO and LUMO of alkene and butadiene were used for formation of the transition state for their right symmetry of the bonding orbital. By inspection of the frontier molecular orbital of the transition state in the Jmol, it could be found that all molecular orbitals constructed in the transition state are formed supra-facially. That is to say two reactants approach each other with their pi orbitals parallel head to head via sigma interactions. P orbitals of both ends of both reactants dis-rotate to form two new sigma bonds symmetrically. This is supported by Woodward–Hoffmann rules which stated that a [4+2] cycloadditon reaction is thermally allowed if ps+qs= 4n+2 or pa+qa=4n+2. 4n+2 is the number of pi electrons used, s and a notations mean that a fragment uses it molecular orbital supra-facially or antasupra-facially. For this reaction, must be 4s+2s which means this reaction only happens if two new bonds formed symmetrically with C2v plane. Orbital overlap integrals provide a quantitative understanding about how much two orbitals/ wave functions overlap. As shown in the MO diagram, overlap integral between symmetric-symmetric (u-u) and asymmetrical-asymmetric (g-g)are non-zero. Overlap of symmetric-asymmetric interaction (u-g) is 0 because the interaction is asymmetric.

Bond Change

All numbers in this section saved the unit Angstrom for convenience. The table outlines all carbon-carbon bond lengths in reactants, transition states and products and how they change. Explanation about the color in the table: red the double bond, orange the single bond, yellow the partial double bond, pale yellow the partial single bond. It is found all double bond length increases and bond order decreases. The only single bond lengthens and become a double bond. Two newly formed single bonds have decreased the length from infinity to partial single bond in the tradition state. All bond lengths changed dramatically near transition state. Typical bond length: sp3-sp3 1.54, sp2-sp2 1.34, sp2-sp3 (in product)1.50, Van der Waal radius of carbon 1.7. Two carbon with Vdw radius 1.7 have 3.4 interaction length, any length shorter than this means two atoms are in interaction like 2.11 in partial single bond in TS, of course, longer than typical C-C single bond.

Synchronous Reaction

At transition state, the vibration is as shown with a negative vibration frequency along the reaction coordinate. This frequency in transition state is an imaginary number but represented as a negative value. It is imaginary number from square root of -1 when solving equations for force constant, k, a negative value.

The vibration with the lowest positive frequency is along their plane. Comparing with the transition state vibration, these vibrations are orthogonal of each other, which can be described as the energy exchange only happens within one normal mode and never exchanges to another. The one with negative frequency describes the formation of two bonds synchronously (hence Diels-Alder reactions are concerted reactions).

Calculation output by PM6

optimized reactant: Media:YXZ_EXP1_DIENE_MINIPM6.LOG Media:YXZ EXP1 DIENE MINIPM6.LOG

optimized product: Media:YXZ_EXP_PRODUCT.LOG

otimized/frequency calculated transition state:Media:YXZ_EXP1_REAL_TS_WITH_MO.LOG

IRC to confirm the transition state: Media:YXZ_EXP2_IRC2.LOG

Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole

MO construction and data presentation

MO and FMO

(Fv611 (talk) The MO diagrams are well constructed, but there should have been some discussion on the difference between the endo and exo transition state and on the electron demand of this reaction. Additionally, you have not labelled the TS MOs consistently in the diagrams and in the table.) MO diagrams of transition states were approximated quantitatively by IRC and single point energy calculation which were demonstrated as well.

Visualisation of Frontier Molecular Orbital of Transition State

Endo-transition state

Exo-transition state

HOMO-1

HOMO

LUMO

LUMO+1

HOMO-1

HOMO

LUMO

LUMO+1

Single point energy and IRC calculation

Energy Calculation of Reactants: Display of MO and Energy

reactants to form exo-product

reactants to form endo-product

MO 40:HOMO of cyclohexadiene

MO 41:HOMO of dioxole

MO 42:LUMO of cyclohexadiene

MO 43:LUMO of dioxole

MO 40:HOMO of cyclohexadiene

MO 41:HOMO of dioxole

MO 42:LUMO of cyclohexadiene

MO 43:LUMO of dioxole

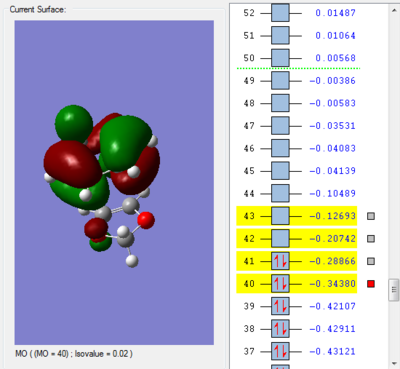IRC Calculation

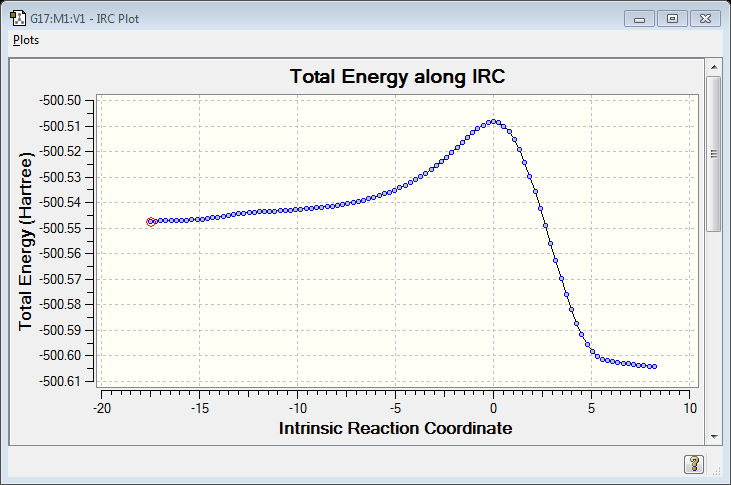
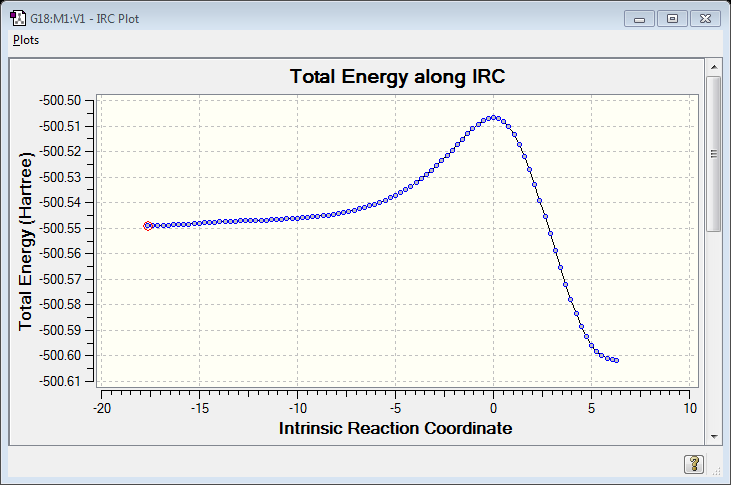
Reaction Thermodynamics

thermochemistry data from Gaussian calculation
	1,3-cyclohexadiene	1,3-dioxole	endo-transition state	endo-product	exo-transition state	exo-product
Sum of electronic and thermal energies at 298k (Hartree/Particle)	-233.303306	-267.044172	-500.306014	-500.395004	-500.303864	-500.394008

Secondary Orbital Interactions

EXO TS MO of HOMO

Endo TS MO of HOMO

Explanation of data and answers to questions

MO analysis

By using single point energy calculation, energies of MOs could be compared under same potential energy surfaces. In the Energy Calculation of reactants, diene and dienophile called for simplicty, (displacement of C-C set larger than 2xVdw radius: >3.5 A) it was found that MOs of their frontier orbitals for bonding are arranged low to high: HOMO of diene, HOMO of dienophile, LUMO of diene, LUMO of dienophile with energy gap 3:4:4 approximately. This is beacuse diene has conjugated pi bond thus smaller HOMO-LUMO energy gap(consistent with calcualtion: 3+4<4+4). Electron donating groups (heteroatoms) in dienophile raised energies of MOs thus its HOMO and LUMO all higher than diene and normal dienophile.
For the FMO in transition state, by doing the Electron Calculation and setting C-C displace ment just at 2xVdw radius, reactants MOs began to overlap. Reactants MOs under calculation were not pure one reactant, sometimes orbitals small in size of another reactant and its enrgy is between two pure MOs of reactants. Finally when setting C-C displacement to distance in transition state in exo transition state, the energy gap between HOMO-1, HOMO, LUMO, LUMO+1 are 4:10:3.
It could be concluded that this is an inverse demand DA reaction for EDG in dienophile. When orbitals began to interact, filled orbitals(bonding orbitals in reactants) energy raise and unfilled orbitals(anti bonding orbitals in reactant) energy lowered because electrons began to appear in the overlapped region. When forming the transition state, new bonding orbitals energies reached a maximum and began to lower to a minimum, new anti-bonding orbital energy lowered to a minimum and began to raise to the highest. In endo-transition sate, because of its lower Gibbs energy, energy gaps between frontier orbitals should be larger, in other words, bonding orbitals lower in energy than exo-TS and anti-bonding higher because interaction of this extent is enough for it to form new bonds and damp energy to form a product. Other energies of stabilization are from secondary orbitals in endo-TS

Nf710 (talk) 23:19, 8 February 2018 (UTC) IT is very good that you have done this analysis well done. You could have presented it much clear rather than just having a single picture. But well done for doing this.

Reaction Thermodynamics

Kinetic product and thermodynamic product are ones have smallest activation energy and largest reaction ernergy. In this case, both are endo product, numerical calculation will be shown soon. However, Diesl Alder reaction could be reversed by taking in and releasing energy. Also interesting are the fastest formed product and the most stable product.
The fastest formed product.
The Arrhenius Equation states that reaction rate constant is related to Ea by k=Ae−Ea/RT. A is frequency factor constant or also known as pre-exponential factor or Arrhenius factor. It indicates the rate of collision and the fraction of collisions with the proper orientation for the reaction to occur. There are two ways to achieve the fastest reaction path. One is the lowest free energy of TS and one is higher rate of collision.
So thermodynamic control involves raising temperature. The most stable product, having less chance of going reversible reaction to products or other dissociation reaction. One has lowest free energy of product and lowest rate of collision to go back to product.

Free energy information could be extracted from Thermochemistry data in output file from Gaussview. and gradient of free energy could be estimate by the vibration frequency in the TS. Gradient from IRC provides gradient in the intrinsic reaction coordinate so not always working right.
Sum energy of reactants: -233.303306+(-267.044172)=-500.347478 Hartree
1 Hartree = 2625.50 KJ/mol
The reaction barrier of a reaction is the energy difference between the transition state and the reactants.
For the endo reaction: -500.347478-(-500.306014)=0.041464 Hartree = 108.8636841 KJ/mol
For the exo reaction: -500.347478-(-500.303864)=0.043614 Hartree = 114.5085066 KJ/mol
The reaction energy of a reaction is the energy difference between the product and the reactants.
For the endo reaction: -500.347478-(-500.395004)=-0.047526 Hartree = -124.7794581 KJ/mol
For the exo reaction: -500.347478-(-500.394008)=-0.046530 Hartree = -122.1644612 KJ/mol
Endo product has both lower activation energy and reaction energy because of secondary orbital interaction.

Collision rate of both directions to get to TS could be understood by the inverse of frequency of vibration the forming bond in TS. Frequency equals square root of k/m. K is the gradient of potential energy. In TS, k from reactants is negative so frequency calculated by Gauss is imaginary. Thus gradient of free energy around TS could also provides an idea about the collision rate but gradient from IRC provides gradient in the intrinsic reaction corrdinate so not always working right.
In this case exo-TS has negative frequency of -530 which is larger than -523 of endo-TS which means the collision rate or dissociation rate to achieve exo-TS is higher. This is because it has less steric to prevent bond forming. However, the difference is small which may be outweighed by free energy. Negative frequency is from negative k because bonds do not exist in TS, it is an imaginary vibration of bond.
It is concluded that endo product is both kinetic and thermodynamic product, not like reaction of simple dienophile. It is also the fastest and most stable product.

Secondary orbital interation

Secondary orbital interactions arises in TS when oxygen in dienophile can donate one pair of electrons in its nonbonding orbital of the correct orrientation into diene's LUMO. This is consistent with bonding interaction of HOMOs of dienophile with diene`s LUMO. This further lowers energy of LUMO of diene and HOMO of TS and helps bonding breaking of HOMO of diene. This is possilble when TS adopt a more steric arrangement in the endo way. However, this stabilization of TS energy outweighs the steric hindrance destabilization in endo TS.

Nf710 (talk) 23:17, 8 February 2018 (UTC) This is not formatted very well and it makes it extremely difficult to read. Sadly your energies are incorrect. I dont know what you have done because it looks like you have calculated them at B3LYP. Other than that you have come to the correct conclusions and had a balanced argument.

Calculation output by B3LYP 621g.d.p

Optimized endo transition state (frequency calculation is done in the same file): Media:YXZ_EXP2_ENDO_TS_631_WITH_MO3.log

Optimized exo transition state (frequency calculation is done in the same file): Media:YXZ_EXP2_EXO_TS631_MOLATEST.log

Energy calulation exo transition state (frequency calculation is done in the same file): Media:YXZ_EXP2_EXO_ENERGY4WITHMO.log

Energy calculation endo transition state (frequency calculation is done in the same file): Media:YXZ_EXP2_ENDO_ENERGY2.log

IRC endo transition state (frequency calculation is done in the same file): Media:YXZ_EXP2_ENDO_IRC4.log.log

IRC exo transition state (frequency calculation is done in the same file): Media:YXZ_EXP2_EXO_IRC4.log

B3LYP optimized dioxole (frequency calculation is done in the same file): Media:YXZ_EXP2_DIXOLE631.LOG

B3LYP optimized cyclohexadiene (frequency calculation is done in the same file): Media:YXZ_EXP2_DIENE631.LOG

B3LYP optimized endo product (frequency calculation is done in the same file): Media:EXP2_ENDO_MINI631_FREQUENCY_CHECK.LOG

B3LYP optimized exo product (frequency calculation is done in the same file): Media:EXP2_EXO_621_MINI.LOG

Exercise 3. Diels-Alder vs Cheletropic

All this exercise use method PM6

Data reprensatation

Optimisation of TS

Optimisation

Optimisation of TS of EXO

Optimisation of TS of Endo

Optimisation of TS of cheletropic

Optimisation of TS of Second Exo

Optimisation of TS of Second Endo

(You have used random frames for your Jmols which suggests you've used someone else's code without understanding what it does Tam10 (talk) 13:36, 4 February 2018 (UTC))

IRC analysis

Table9. Approach trajectory of 3 reactions and their IRC
Approach trajectory of endo product formation	Endo product formation IRC

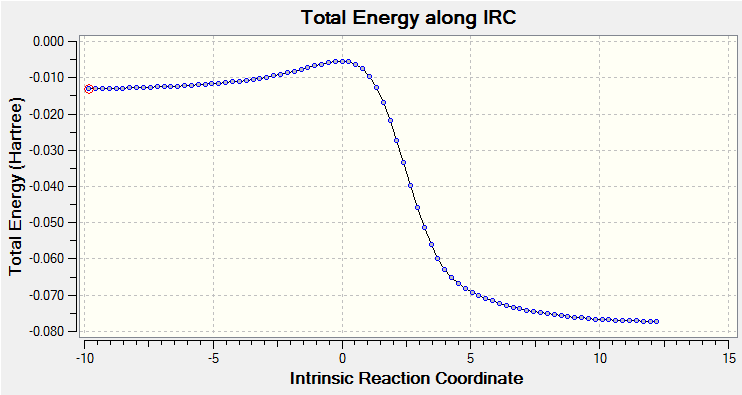
Approach trajectory of exo product formation	Exo product formation IRC

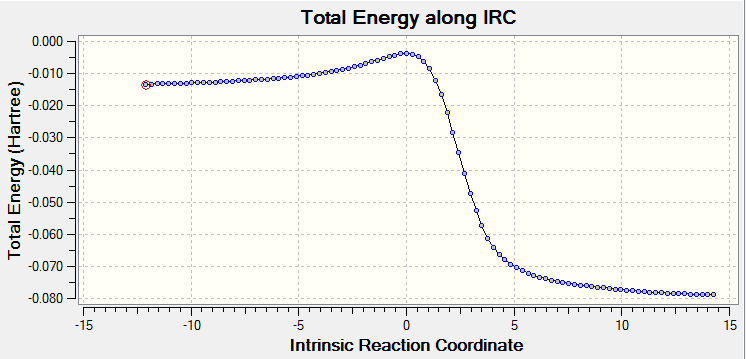
Approach trajectory of cheletropic product formation	Cheletropic product IRC

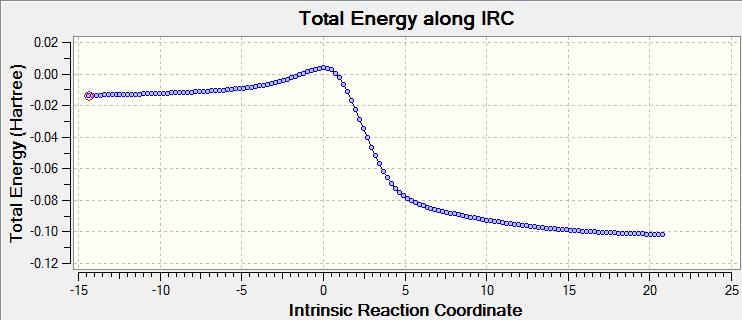
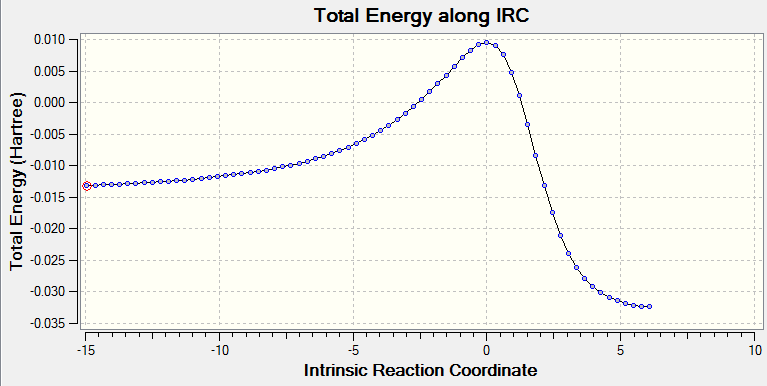
Approach trajectory of exo product using second diene	Second diene exo product IRC

Approach trajectory of endo product using second diene	Second diene endo product IRC

Thermochemistry data

(You were asked to use the sum of electronic and thermal free energies. Your results are a bit off as a result Tam10 (talk) 13:36, 4 February 2018 (UTC))

Sum of electronic and thermal energies of reactants, TS, and products by Calculation PM6 at 298K
Components	Energy/Hatress	Energy/kJmol^-1
SO2	-0.091033	-239.0071415
Xylylene	0.21851	573.698005
Reactants energy	0.127008	333.459504
ExoTS	0.138518	363.679009
EndoTS	0.136783	359.1237665
Cheletropic TS	0.146	383.323
Exo TS from second butadiene	0.151054	396.592277
Endo TS from second butadiene	0.148031	388.6553905
Exo product	0.066032	173.367016
Endo Product	0.067003	175.9163765
Cheletropic product	0.043585	114.4324175
Exo product from second butadiene	0.112672	295.820336
Endo product from second butadiene	0.10999	288.778745

Activation energy and reaction energy(KJ/mol) of five reaction paths at 298K
	Exo	Endo	Cheletropic	Exo from second butadiene	Endo from second butadiene
Activation energy	30.219505	25.6642625	49.863496	63.132773	55.1958865
Reaction energy	-160.092488	-157.5431275	-219.0270865	-37.639168	-44.680759

Reaction profile

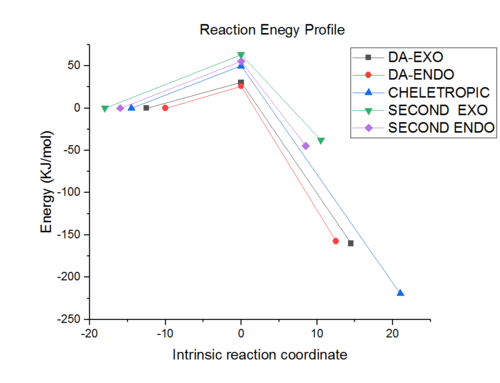
Explanation of data and answers to questions

Competing reactions analyse with help of IRC

This exercise is focused on comparing five possible paths: Diesl alder reaction by exo, DA by endo, cheletropic, DA by endo by second diene, DA by exo by second diene and how they they copetes. By inspection of energy graph, the kinetic product is DA endo with least activation energy and second lowest product energy. The thermodynamic product is the cheletropic product which has lowest product energy and third lowest activation energy. The preferred reaction path should only be specified under kintic or thermodynamic control. Details in Exercise 2.
IRC can give generalised idea about how stable the product is and how hard TS can be reached because it measures many steps TS needed to go to reactant and product.

Rationalization of free energy surface by FMO theory

These five reaction paths can be firstly divided into two classes accroding to different parts of conjugated 4 pi bond. Here for simplicity only considering two dienes inside and outside the ring separately. And also the MO of two dienes treated separately.
1. diene outisde ring
The first three reactions used diene outside the ring or at end. These three reactions are more competing than the other two because diene outside the ring is more accessible for less steric and reorganization of structure and benzene formation from xylylene giving a larger stabilization in energy.
Two DA reactions in this class uses HOMO of SO2 and cheletropic reaction uses LUMO. Then diene uses HOMO and LUMO according to the SO2. For DA endo reaction, the lowest TS of three benefited from secondary orbital interaction of one pi cloud localized on oxygen, the one not in bonding interaction. Cheletropic reaction uses pi cloud delocalzed on soft sufurhas higher TS for larger gap of its LUMO and diene`s HOMO. However it has most stable product because two strong S=O bonds remain there. All reactions form new two bonds but cheletropic reaction destory least bonds and has least steric hindrance.
2. diene in ring
These two DA reactions uses dienes in ring and are far less competitive for the unstable product and high activation energy.

Dimerization and isomerization

O-xylylene is highly reactive because it can dimerize to a dimer and isomerize via electrocylic reaction to form a benzocyclobutenes. This two reactions can also benefited from formation of benzene in product like the first three reactions. And, product of these five reactions are all more stable than the two second DA mechanism reactions for the aromatic product instead of the aromatic TS only. So the second two DA reactions can hardly be seen.

(You must back up claims about reactivity with calculations or literature Tam10 (talk) 13:36, 4 February 2018 (UTC))

Calculation output by PM6

PM6 optimized endo transition state: Media:YXZ_EXP3_EXOPM6MINI.LOG

PM6 optimized exo transition state: Media: YXZ_EXP3_DAENDO_TS1.LOG

PM6 optimized cheletropic transition state:Media:YXZ_EXP3_CHELE_TS.LOG

PM6 optimized Second exo transition state: Media:YXZ EXTENSION TS.LOG

PM6 optimized Second endo transition state:Media:YXZ_EXTENSION_ENDO_TS.LOG

PM6 optimized endo transition state IRC: Media:YXZ_EXP3_ENDO_IRC.log

PM6 optimized exo transition state IRC:Media:YXZ_EXP3_EXO_IRC.log

PM6 optimized cheletropic transition state IRC: Media:YXZ_EXP3_CHELE_IRC.log

PM6 optimized second endo transition state IRC: Media:YXZ_EXTENSIONENDO_IRC.log

PM6 optimized second exo transition state IRC:Media:YXZ EXTENSIONEXO IRC.log

PM6 optimized endo product: Media:YXZ_EXP3_ENDO_PRODUCTLATEST.LOG

PM6 optimized exo product:Media: YXZ_EXP3_EXOPM6MINI.LOG

PM6 optimized cheletropic product:Media:YXZ_EXP3_CHELE_MINI2.LOG

PM6 optimized second endo product: Media:YXZ_EXTENSION_ENDO_PRODUCT.LOG

PM6 optimized second exo product:Media: YXZ_EXTENSION_PRODUCT1.LOG

PM6 optimized SO₂:Media: YXZ_EXP3_SO2MINI2.LOG

PM6 optimized xylylene:Media: YXZ_EXP3_DIENEMINI2.LOG

Further work

1. Ring opening of a cyclobutene
Reaction proceeds with conrotation. This reaction involves forming of Möbius aromatic transition state involving one antarafacial four-electron component. Pi bond of double bond overlap with sp3 C-C anti bond followed by the rotation of sigma bond of double and rotation of sp3 bonding of C-C. To form a monocyclic array of molecular orbitals which has odd number of out-of-phase overlaps, Mobius aromatic TS, forming HOMO of butadiene, rotation is restricted to conrotation. Diene formed then have different phases of p orbitals on terminal.
2. Photochemical reaction
Reaction proceeds with disrotation. When such a diene absorbs light of right frequency, an electron will be exiced from HOMO to LUMO. Now this diene has new HOMO and LUMO of ψ3 and ψ4 of ground state. In this case, To form Möbius aromatic transition state, sigma bond will choose disrotation to form the new bond p orbitals of different phase at ends. And now the transition state is better understood by a conical intersection in 2D PES accompanied by a change of symmetry.
3.Opening of the cyclopropyl cation
Reaction proceeds with dis-rotation. It forms a Huckel aromatic TS of 2 electrons and form a product of allylic cation which has same phases on terminal p orbital and stabilized by conical form. HOMO of OTs- helps stabilizing form of TS and leaves just after that.
4. Opening of the cyclopropyl cation with hetero-atoms
Conrotation needed to form Möbius aromatic transition state and gives a product with different phases at ends and has HOMO of C2v and pi cloud localized.

Conclusion

In this work, different calculations are studied. Optimization to find the right structure. Frequency to check if it is correct. IRC to visualize free energy surface on intrinsic coordinate. Energy to compare different molecules on one potential surface.
Important information can be extracted by using Gaussview like visualization of MO to study the FMO theory and symmetry of reaction. Thermochemistry data like Gibbs free enrgy, zero point energy and enthalpy an so on. Visualization of vibration modes can give the reaction coordinate.
For pericyclic reactions, symmetry rules, Hammond's postulate, bond forming and rotation have been studied and there is still something to be explored like other thermal pericyclic reactions and light-induced pericyclic reactions.

Reference

1. file://icnas4.cc.ic.ac.uk/xy3513/9789048138609-c2.pdf