Transition states and reactivity

Introduction

For a potential energy curve with only one variable, the curve is considered to be the energy profile. If more than one geometric coordinates associate with potential energy, the three-dimensional surface is called potential energy surface. For a nonlinear molecule, there is 3N-6 independent geometric variables. The transition state is the maximum point on the surface, connecting two minima, reactant and product. These stationary points (transition state, reactant and product) are defined as zero first derivative ( $\frac{\partial E}{\partial R}$ = 0), showing that the gradient is zero.

$\frac{\partial E}{\partial R} = - F$
Equation.1, first derivative

The gradient is related to force acts on the atoms, and the negative sign indicates the force is in the direction of lowering potential energy. In order to distinguish them, curvatures (frequencies) at these points are determined by second derivative.

$\frac{\partial^{2} E}{\partial R^{2}} = k$
Equation.2, second derivative

Second derivatives are hold in the Hessian matrix, and by diagonalizing the Hessian matrix, force constant k can be determined as well as the frequency by Eqn.3. The saddle point (transition state) has negative curvature ( $\frac{\partial^{2} E}{\partial R^{2}} < 0$ ), while the minima have positive curvature ( $\frac{\partial^{2} E}{\partial R^{2}} > 0$ ).

Energy, electronic structure and properties of molecules can be determined by solving Schrödinger’s equation. The computational method is used to solve the equation by deciding to use different level of theory (Hamiltonian operator) and basis set (mathematical description of wavefunction). In this page, two optimisation methods were adopted, PM6 and B3LYP/6-31G(d). For PM6, it is a semi-empirical method, which is based on Hartree-Fock theory. ^[2] It solves the many-electron equation by expanding the coefficient of linear combination of atomic orbitals (LCAO) and simplifies with Born–Oppenheimer approximation. The full HF calculation is too expensive, therefore PM6 is simplified by neglecting two-electron part of Hamiltonian, and further simplification can be applied for π-electron system by Hückel method. It is overall a quick but not reliable method. B3LYP/6-31G(d) is based on density functional theory (DFT), which associates with HF theory and an additional term, exchange-correlation energy.^[3] B3LYP is the choice of exchange-correlation energy and 6-31G is the basis set. DFT is sufficient accurate but it is an expensive method.

In this page, Gaussian, the computational method, is used to interpret the mechanisms of four pericyclic reactions. This technique is able to identify whether the bond formation is synchronous or asynchronous, formation of kinetic or thermodynamic product and whether the proposed reaction pathway is favourable.

Nf710 (talk) 23:43, 22 March 2018 (UTC) You have clearly read beyond the script here well done. Some equations would have been good. When you diagonalise the hessian your are changing your coordinate basis into the noraml modes. which are then linear combinations of the degrees of freedom.

Exercise 1: Reaction of Butadiene with Ethylene

(Fv611 (talk) Overall you have done a good job. However you have used your B3LYP optimisation of ethene instead of the PM6 one, which led you to the wrong MO energies.)

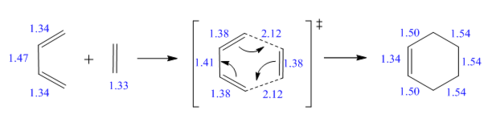
The first reaction is the classical [4+2] cycloadditon (Scheme.1), which is also called Diels-Alder reaction. This reaction was investigated by guessing the transition state first and finding the optimised product. Both reactants and TS were optimised at PM6 level, and a frequency calculation and Intrinsic Reaction Coordinate (IRC) were analysed to ensure that a correct TS was obtained. Finally, the product was optimised at PM6 level.

Optimisation and Calculation

Optimised structures of reactants, TS and product at PM6 level

Butadiene

Ethene

TS

Product

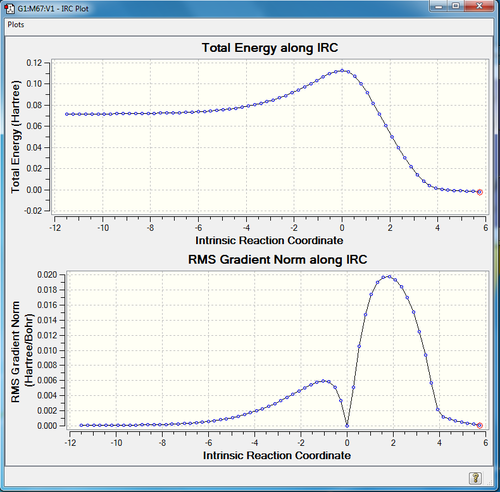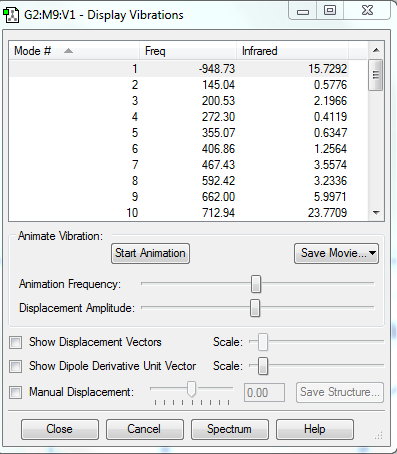
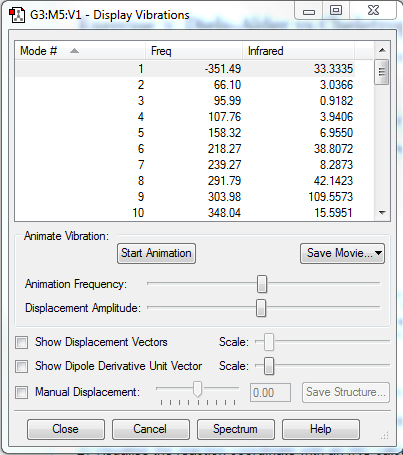
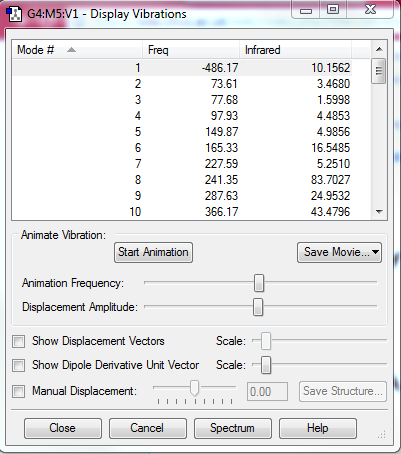
Figure.1, Frequency calculation of TS	Figure.2, IRC (total energy and RMS gradient) of TS

Fig. 1 shows that only one frequency is negative, indicating the transition state. IRC is the minimum energy pathway on the potential energy surface, starting from the first-derivative stationary point, TS, and calculating in both direction until reaching two minima, reactants and products. Fig. 2 illustrates the total energy and RMS gradient along IRC, and the gradients of reactants, products and TS are all zero, confirming a successful and asymmetric IRC was performed.

MO Analysis

HOMO and LUMO of reactants and HOMO/-1, LUMO/+1 of transition states

Butadiene (HOMO)

Butadiene (LUMO)

Ethene (HOMO)

Ethene (LUMO)

TS (HOMO-1)

TS (HOMO)

TS (LUMO)

TS (LUMO+1)

By visualising MO of reactants and TS, part of the MO was constructed in Fig.3 (MO). The calculated orbital energies at PM6 level are labelled in grey, however, due to the low optimisation level, these energies are only a rough guide to the MO diagram. Although the energies are not accurate, it still provides an evidence of mixing. The dotted orbitals are the MOs without mixing, while the solid-line orbitals are the ones with predicted mixing.

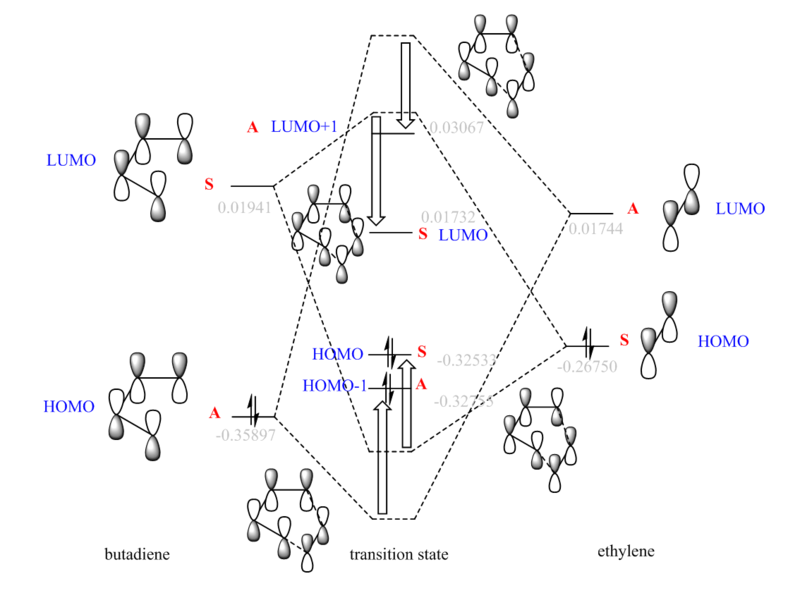
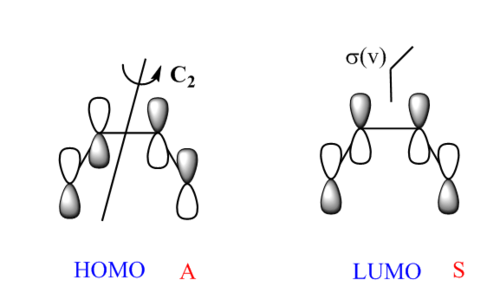
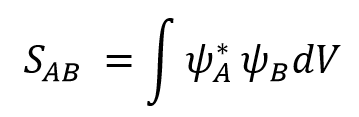
The symmetry of each orbital can be identified with its symmetry axis or plane. The HOMO of butadiene is antisymmetric as it has C2 symmetry, while the LUMO is symmetric as it contains σ(v) symmetry plane. (Fig.4) Only the orbitals with same symmetry could combine to form new MOs. The orbital overlap integral is represented by Eqn.4^[4], and it is zero when the overall interaction is antisymmetric. The symmetric-antisymmetric interaction is antisymmetric, integrating to zero (forbidden reaction). The symmetric-symmetric and antisymmetric-antisymmetric interaction are symmetric, resulting to non-zero integral (allowed reaction). The Woodward-Hoffmann rules states that in a thermally allowed reaction, the total number of (4q+2)_s and (4r)_a components must be odd, where the suffix s stands for suprafacial (forming bond on same face), and a for antarafacial (forming bond on opposite face). By applying Woodward-Hoffmann rules, this reaction is proved to be thermally allowed.

(4q+2)s+(4r)a
=1+0
=1
=thermally allowed reaction

Bond Length Analysis

Table 1. Bond length of reactants, transition states and product *(refer to Scheme.1)*
Structure	sp³-sp³ C-C /Å	sp³-sp² C-C /Å	sp²-sp² C=C /Å	sp²-sp² C-C /Å
Butadiene	n/a	n/a	1.34, 1.34	1.47
Ethene	n/a	n/a	1.33	n/a
TS	2.11, 2.11 (forming single bond)	n/a	1.38, 1.38 (partially double bond); 1.38 (partially double bond)	1.41 (partially double bond)
Product	1.54, 1.54	1.50, 1.50	1.34	n/a
Typical value	1.54	1.50	1.34	1.47

Table 2. Van der Waals radius of Carbon
Van der Waals radius of Carbon
One carbon atom /Å	1.70	Two carbon atoms /Å	3.40

Comparing the bond length of reactants and TS, the reactants show typical bond length of sp²-sp² C=C, sp³-sp² C-C and sp²-sp² C=C. In the TS, C10-C12 is shortened due the change from sp³-sp³ single bond to sp²-sp² double bond, while C7-C10 and C12-14 show an elongation because sp²-sp² double bonds are changed into sp²-sp³ single bonds. C1-C4 becomes longer as it converts from sp²-sp² double bond to sp³-sp³ single bond. The distance between C4 and C7/ C1 and C14 is both 2.11 Å, which is shorter than sum of Van der Waals radius of two carbon atoms (Table.2), indicating that two molecules are approaching to each other and forming a partial bond. The product shows typical sp³-sp³ C-C, sp²-sp³ C-C and sp²-sp² C=C bond length.

a	b
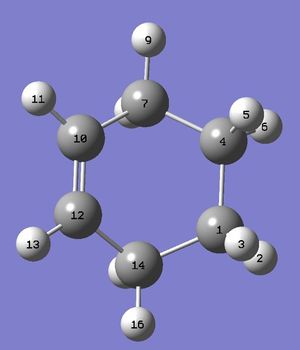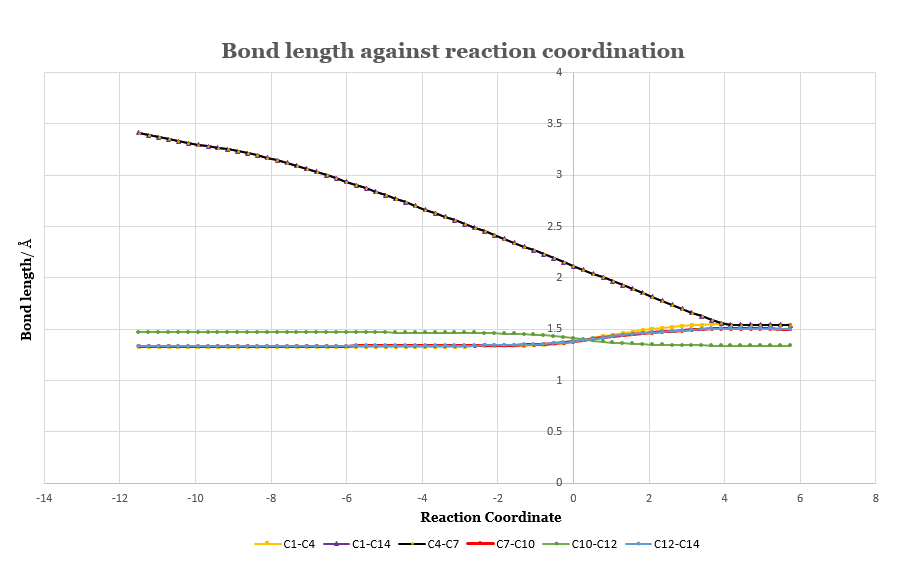
Figure.5, a) The change of bond length with respect to reaction coordinate. b) Numbering of atoms of the product

Fig.5 illustrated the change of bond length along the reaction coordinate by analysing IRCs of each bond. C1-C4 (purple) and C4-C7 (black) starts from 3.40 Å, where no bond is formed, and then reaching TS at 2.11 Å. The product is formed when the bond length is at 1.54 Å. The rest of the bonds corresponds to the explanation in the previous section.

Vibration

By visualising the vibration of TS and motion picture of Fig.6, the formation of two bonds are synchronous.

Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole

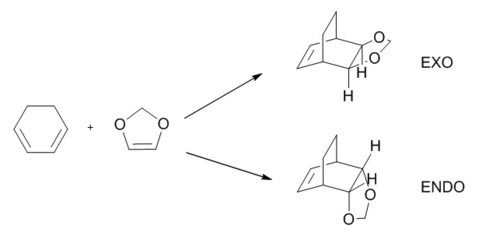
This Diels-Alder reaction is stereospecific, leading to endo and exo adducts. The more favourable reaction pathway is examined by the calculating activation energy and free energy. Reactants, TS and products were optimised first with PM6 following by using B3LYP/6-31G(d).

Optimisation and Calculation

Optimisation of reactants, TS and products

Cyclohexadiene

1,3-Dioxole

Endo TS

Exo TS

Endo Product

Exo Product

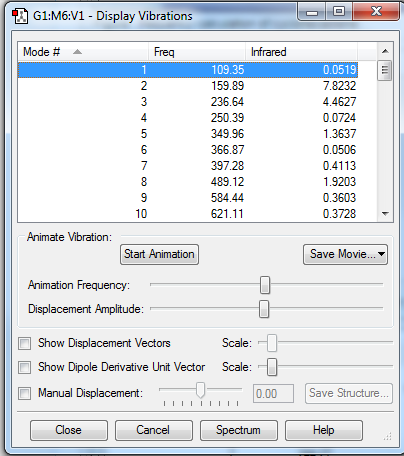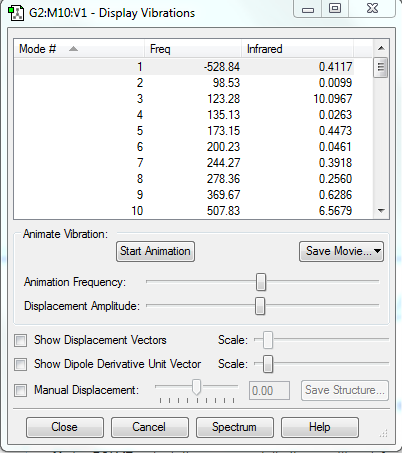
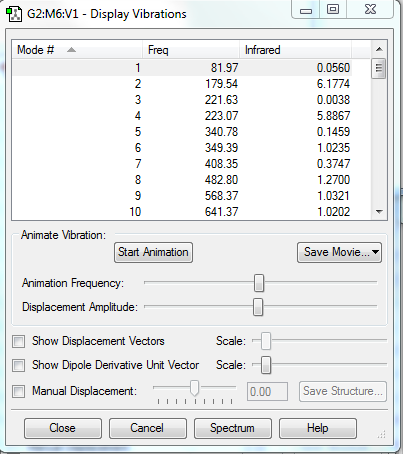
There is no imaginary frequency for all the reactants and products, and there is only one negative frequency for each TS, confirming that all of them were well optimised.

MO Analysis

HOMO and LUMO of reactants and HOMO/-1, LUMO/+1 of ENDO/EXO transition states

Cyclohexadiene (HOMO)

Cyclohexadiene (LUMO)

1,3-Dioxole (HOMO)

1,3-Dioxole (LUMO)

ENDO TS (HOMO-1)

ENDO TS (HOMO)

ENDO TS (LUMO)

ENDO TS (LUMO+1)

EXO TS (HOMO-1)

EXO TS (HOMO)

EXO TS (LUMO)

EXO TS (LUMO+1)

MOs of reactants and transition states
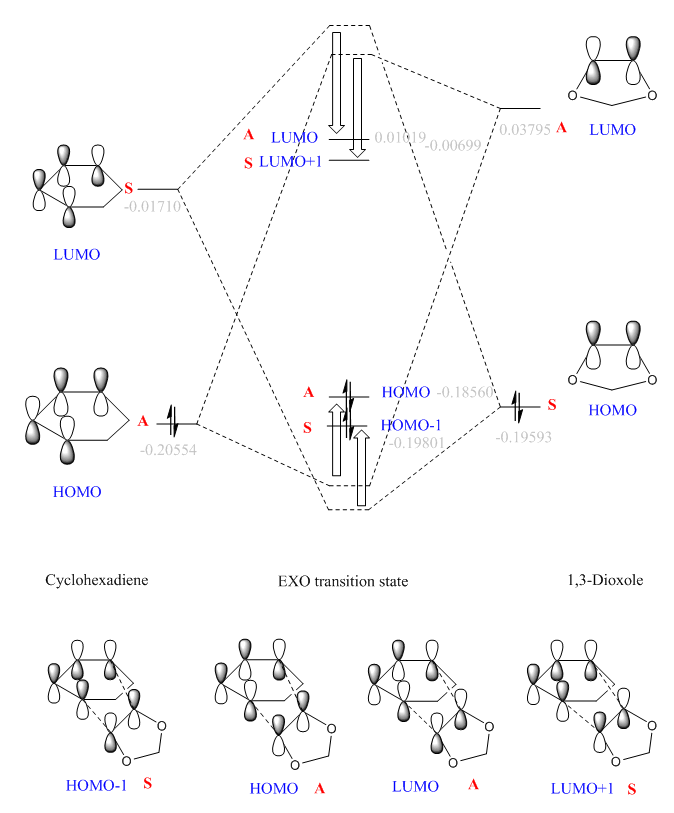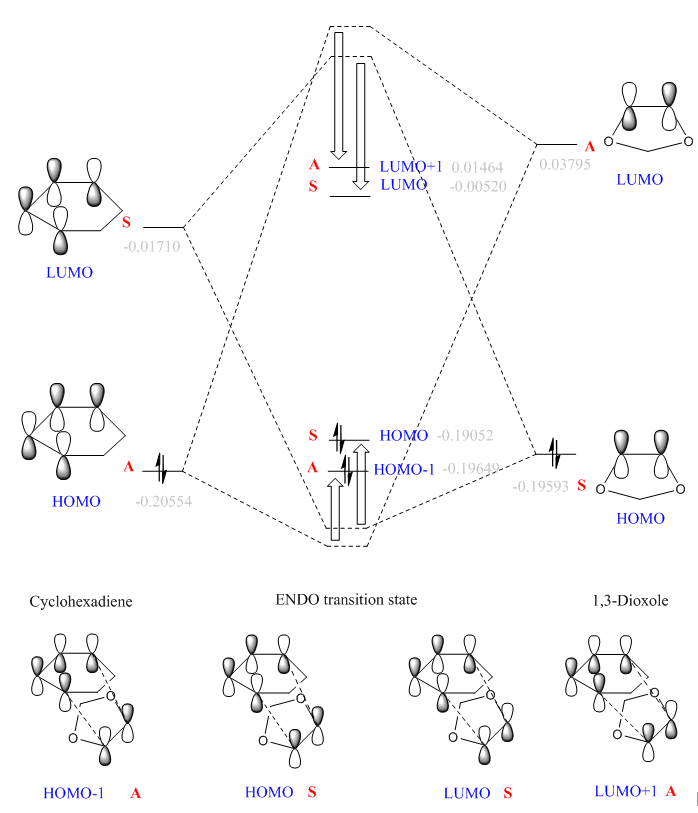
Figure.7, MO diagram of Endo TS	Figure.8, MO diagram of Exo TS

By visualising MOs of reactants and TSs, the MO diagrams of endo and exo TSs were constructed. The calculated orbital energies (in grey) gave a rough guide to the energy difference between orbitals. The orbital energies of HOMO/HOMO-1 and LUMO/LUMO+1 of two TSs are similar, but the actual shapes shown in jmol are different (in later section). The HOMO of endo TS is slightly more stabilised than that of exo TS.

(Fv611 (talk) Good MO diagrams. Could have discussed more the differences between exo and endo conformations in terms of relative MO energies.)

Inverse Demand DA Reaction

For a standard DA reaction, the electron rich component is diene and the electron poor component is dienophile. The HOMO of diene and the LUMO of dienophile are similar in energy and interact strongly. However, for a DA reaction with inverse electron demand, the electron rich component is dienophile and the electron poor component is diene.^[5] Then the more strongly interacting frontier orbitals are the HOMO of dienophile and the LUMO of diene. In this reaction, the dienophile is 1,3-dioxole, and the electron donation from lone pair of oxygen atoms results in more electron rich dienophile. The single point energy calculation confirms this suggestion.

Table.3, Single point energy of HOMO/LUMO of reactants
Molecule	Energy of HOMO/a.u.	Energy of LUMO/a.u.	Difference of LUMO_diene and HOMO_dienophile	Difference of HOMO_diene and LUMO_dienophile
Cyclohexadiene	-0.20601	-0.01800	0.17815	0.24265
1,3-Dioxole	-0.19615	0.03664	0.17815	0.24265

Nf710 (talk) 23:49, 22 March 2018 (UTC) Nice this is well done and clear.

Energy Analysis

Table.4, Gibbs free energies of reactants, TSs and products using B3LYP/6-31G(d)
Molecule	Gibbs free energy/Hartrees	Gibbs free energy/kJmol^-1
Cyclohexadiene	-233.324375	-612593.193227
1,3-Dioxole	-267.068644	-701188.778236
Reactants (total)	-500.393019	-1313781.971463
Endo TS	-500.332149	-1313622.15727
Exo TS	-500.329163	-1313614.31752
Endo Product	-500.418694	-1313849.381181
Exo Product	-500.417319	-1313845.77112

Table.5, Activation energies and ΔG of two reactions using B3LYP/6-31G(d)
State	Activation energy /kJmol^-1	ΔG /kJmol^-1
Endo	159.8	-67.4
Exo	167.7	-63.8

The kinetic product is the one with lower activation energy, leading to faster reaction, and the thermodynamic product is the one with more negative ΔG, which forms more stable product. The calculation of energies in Table.5 illustrates that the endo product has lower activation energy and more negative ΔG, indicating that endo product is the kinetic product as well as thermodynamic product

HOMOs of endo and exo TSs

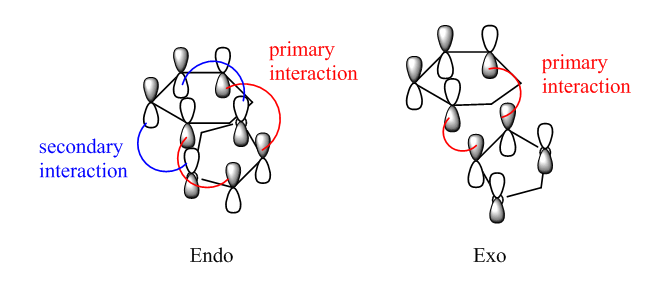
Endo TS

Exo TS

Figure.9, graphic illustration of primary/secondary interactions of HOMOs.

There is only primary interaction in exo TS, while the secondary interaction is also observed in endo TS. The secondary interaction stabilises the endo TS (Fig.9), resulting in faster formation of endo TS and confirming that the endo product is more kinetically favourable.

Nf710 (talk) 23:53, 22 March 2018 (UTC) Good section, you could have gone into more detail about the thermo and kenetic theory. But otherwise a very good section.

Exercise 3: Diels-Alder vs Cheletropic

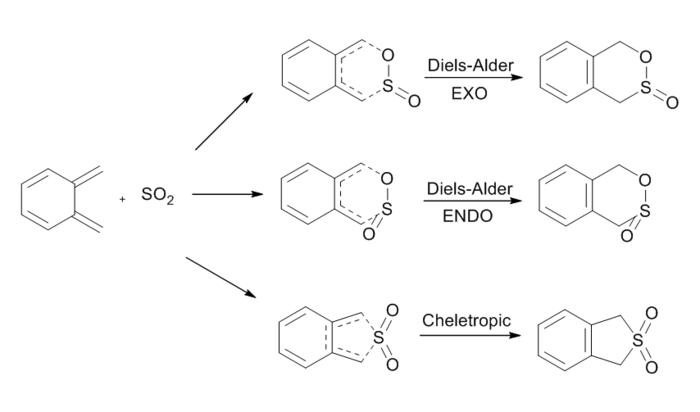
For this reaction, three products were examined, including endo and exo products of DA reactions and cheletropic product. Energy calculations were carried out to identify the most favourable reaction pathway. All the reaction species were optimised at PM6 level. The extension investigated the possibility of DA reaction of a second cis-butadiene in o-xylylene. The activation energies and Gibbs free energies were calculated to suggest the viability of the reactions.

Optimisation and Calculation

Optimisation of three TSs

DA-Exo

DA-Endo

Cheletropic

IRC of three TSs
DA-Endo TS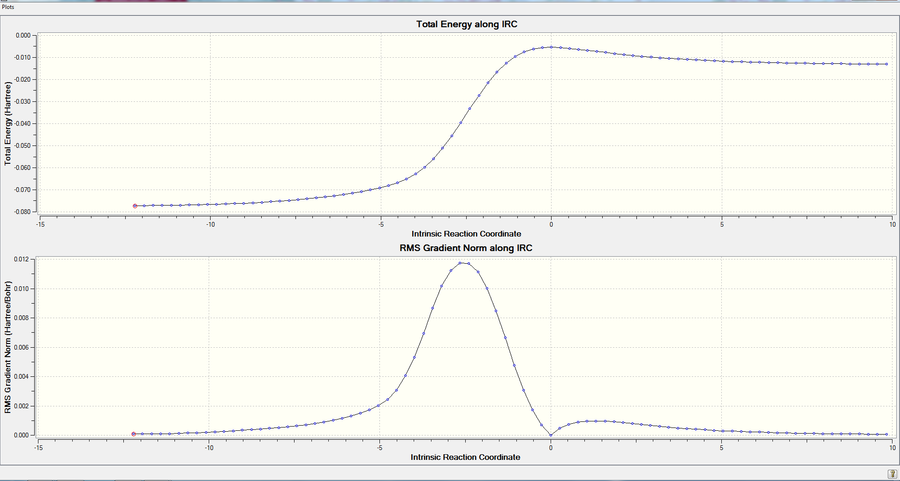
DA-Exo TS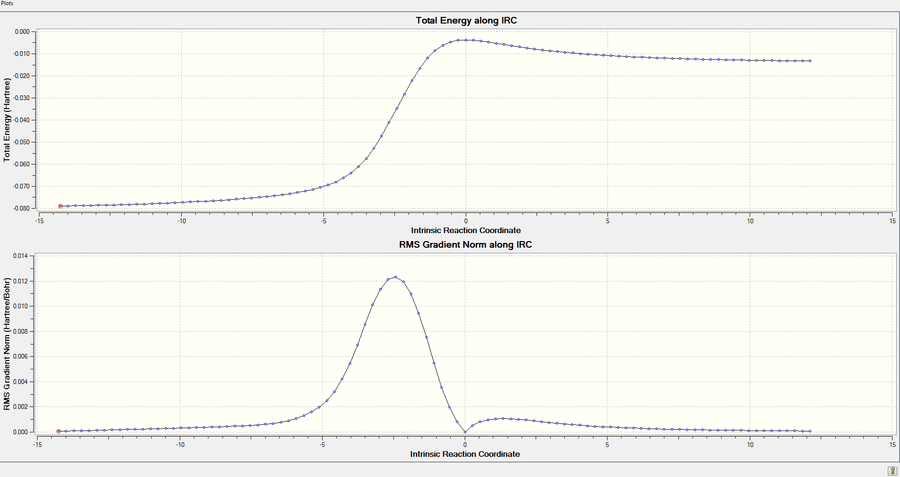
Cheletropic TS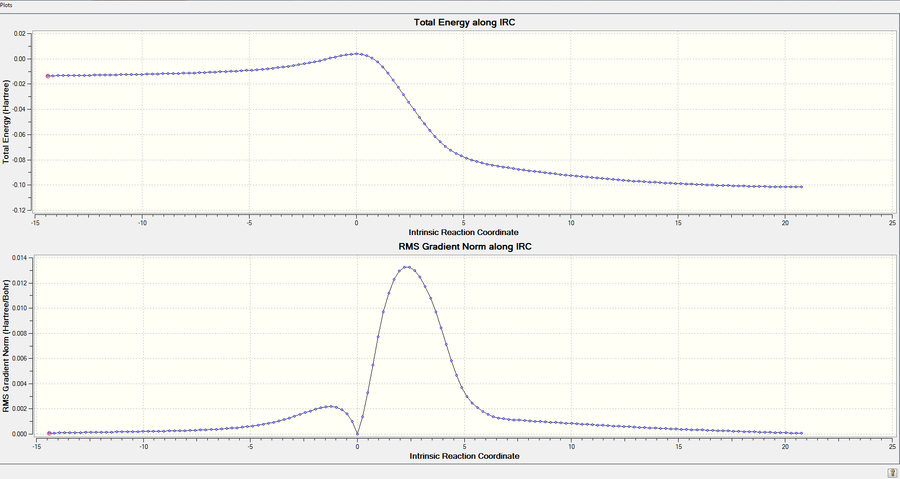
Figure.10, IRCs of three TSs

All IRCs were successful asymmetric graphs. The endo and exo DA TS starts from product to reactant and the cheletropic TS starts from reactant to product. The approach trajectories are shown as motion pictures on the right.

Energy Analysis

Table.6, Gibbs free energies of reactants, TSs and products at PM6
Molecule	Gibbs free energy/Hartrees	Gibbs free energy/kJmol^-1
o-Xylylene	0.178816	469.481444
SO₂	-0.119268	-313.1381579
Reactants (total)	0.059548	156.343286
Endo TS	0.090559	237.762673
Exo TS	0.092077	241.748182
Cheletropic TS	0.099059	260.079424
Endo Product	0.021697	56.9654778
Exo Product	0.021452	56.3222303
Cheletropic product	0.000007	0.0183785014

Table.7, Activation energies and ΔG of two reactions at PM6
State	Activation energy /kJmol^-1	ΔG /kJmol^-1
Endo	81.4	-99.4
Exo	85.4	-100.0
Cheletropic	103.7	-156.3

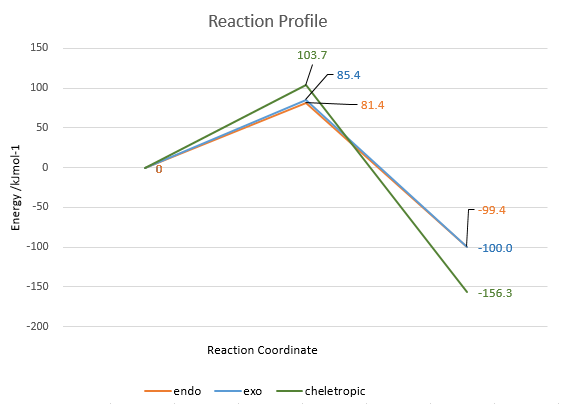
Figure.11, reaction profile of three reactions

By plotting the energy profile (Fig.11), the endo product is the kinetic product as the activation barrier is the lowest. The ΔG of exo product is similar to endo product, indicating that endo and exo products have same thermodynamic stability. The thermodynamic product is the cheletropic product as the ΔG is the most negative one. The energy of o-xylylene is very high, indicating that it is highly unstable. Therefore, by examining IRCs, the 6-membered ring is converted from 8π electrons (4n, antiaromatic) to 6π electrons (4n+2, aromatic), resulting in more stable structures. The required cis-butadiene structure is already present in the o-xylylene, so it accelerates the DA reactions.

Extension

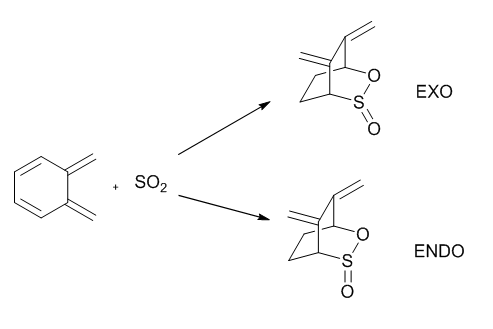
Scheme.4, reaction scheme of o-Xylylene with a second cis-butadiene fragment and SO₂

Optimisation

Optimisation of Endo and Exo TSs and products

Endo TS

Exo TS

Endo Product

Exo Product

Energy Analysis

Table.8, Gibbs free energies of reactants, TSs and products at PM6
Molecule	Gibbs free energy/Hartrees	Gibbs free energy/kJmol^-1
Endo TS	0.102071	267.987431
Exo TS	0.105053	275.816673
Endo Product	0.065611	172.261694
Exo Product	0.067306	176.711916

Table.9, Activation energies and ΔG of two reactions at PM6
State	Activation energy /kJmol^-1	ΔG /kJmol^-1
Endo	111.6	15.9
Exo	119.5	20.4

Both of the reactions has positive ΔG, which requires energy from the environment to proceed the reaction, and the activation energies are much higher than previous DA reactions, suggesting that the DA reaction of cis-butadiene within the ring is kinetically and thermodynamically unfavourable.

Conclusion

Gaussian is powerful in applying the computational method to carry out pericyclic reactions. Different optimisation methods (PM6 and B3LYP) can be adopted to optimise reactants, TSs and products to the required level of precision. The structures can be checked by frequency calculation, as one imaginary frequency appears in TS. The IRC shows the energy profile, and the activation energy and Gibbs free energy can be calculated to predict the most favourable reaction pathway. Information including shape of MOs and bond length is also available, so a MO diagram is constructed easily.

In exercise 1, Woodward-Hoffmann rules and Frontier molecular orbital theory are confirmed experimentally. The reactions in exercise 2 concludes that the endo product is the kinetic and thermodynamic product, and the DA reaction is with inverse electron demand. The reactions in exercise 3 infer that the endo product is the kinetic product and the cheletropic product is the thermodynamic product. Due to the high activation energy barrier of cheletropic TS, the endo product is more likely to form. The cis-butadiene fragment within the ring is too steric to perform DA reactions.

Gaussian is also viable for other pericyclic reactions such as electrocyclic reactions.

Reference

↑ J. McDouall, Computational Quantum Chemistry: Molecular Structure and Properties in Silico, Royal Society of Chemistry, Cambridge, 2013, ch.1, pp.1-62
↑ C.A. Coulson, B.O’Leary, R.B. Mallion, Hückel theory for organic chemists, Academic Press, London, New York, 1978
↑ K. Kim and K. D. Jordan, J. Phys. Chem., 1994, 98, 10089–10094.
↑ P. W. Atkins and J. De Paula, Physical Chemistry, 2009.
↑ A. T. Dang, D. O. Miller, L. N. Dawe and G. J. Bodwell, Org. Lett., 2008, 10, 233–236

Appendix