Rep:Wtc14

Introduction

Gaussian can been used to locate and characterize transition structures for a variety of pericyclic reactions. It is able to optimize the molecular geometry and calculate the vibrational frequency of a compound based on Born Oppenheimer approximation where the electronic distribution of a molecule move instantaneously to the movement of nuclei. Potential energy surface can be plotted using quantum chemistry by calculating the energy as a function of positions of the nuclei.

Geometry optimization will lead to a local minimum which may be a global minimum or a transition state of the product. We can tell which of the minimum we got using to methods. First, we can tell from the potential energy surface(PES). For a global minimum, energy will rise in all direction from that point of minimum on the PES. Whereas for a transition state, the energy will decrease in one direction which is the reaction path on the PES. Secondly, by performing a frequency calculation on Gaussian. For a global minimum, we will have all positive frequency whereas for a transition state we will have one imaginary frequency which is due to the negative value of secondary derivative of energy(a maximum on the PES).

Nf710 (talk) 22:49, 14 December 2016 (UTC) You need to talk about derivatives here

Exercise 1

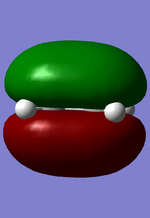
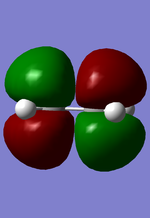
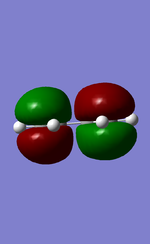
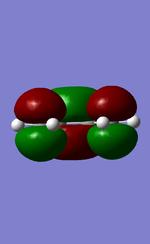
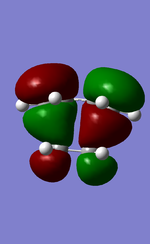
MO diagram for the formation of butadiene/ethene TS

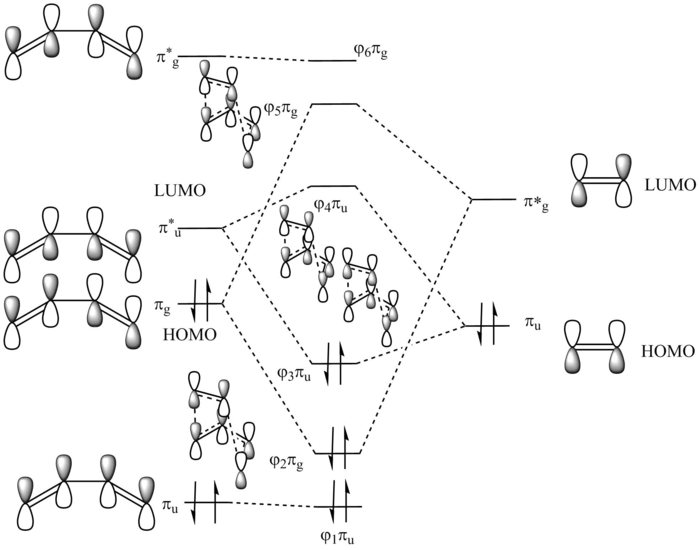Diagram 1: MO diagram for the formation of the butadiene/ethene TS.

MOs:

Name of Compound	Orbital	Symmetry	MO Images	JMol Images
Ethene	HOMO	u
Ethene	LUMO	g
Butadiene	HOMO	g
Butadiene	LUMO	u
TS	second HOMO	symmetric
TS	HOMO	unsymmetric
TS	LUMO	unsymmetric
TS	Second LUMO	symmetric
Table 1: MOs of the reactants and TS.

Symmetry of the reacting orbitals of both reactants must be the same for the reaction to be allowed. The HOMO of butadiene(g) interact with the LUMO of ethene(g) to produce the second HOMO and second LUMO of TS. LUMO of butadiene(u) interact with the HOMO of ethene(u) to produce the HOMO and LUMO of the TS. The overlap integral equals to 1 for same symmetry overlap of orbitals(ie ungerand-ungerand orbitals and gerand-gerand orbitals) and equals to 0 for different symmetry overlap of orbitals(ie gerand-ungerand orbitals and vice versa).

Bond Length Measurement

Bond Length

Compound	Images	Bond Length
Ethene		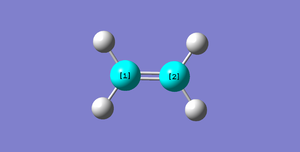C1C2=1.32732Å
Butadiene		C1C2=C3C4=1.33526Å
Butadiene		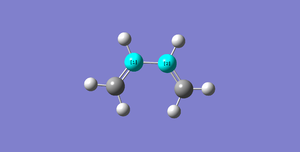C1C2=1.46834Å
TS		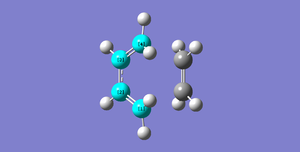C1C2=C3C4=1.37977Å, C2C3=1.41110Å
TS		C1C2=1.38177Å
TS		C1C2=C3C4=2.11478Å
Product		C2C3=1.33702Å, C1C2=1.50077Å, C3C4=1.50095Å
Product		C1C2=1.53711Å, C2C3=1.53450Å, C3C4=1.53720Å
Table 2: Bond length measurements.

All double bonds elongate to form a single bond and all single bonds shorten to form a double bond Typical sp3 and sp2 C-C bond lengths are 1.544 Å and 1.337 Å . The Van der Waals radii of carbon is 1.7 Å . The interatomic distance between the reacting carbons (2.11 Å) are shorter than the Van der Waals radii (3.4 Å). This means that the reacting carbons are approaching each other to react.

Vibration

Vibration

Type of Frequency	Vibration	Description
Imaginary Frequency		The imaginary frequency is taken from the negative frequency. It shows the vibration mode that lead to the transition state of the reaction. Stretching of C=C and shortening of C-C bonds in both reactants can be seen. This compliments to the trend of the change in bond lengths from reactants to the final product shown above. There is also an out-of-plane bend involving the reaction centres, bring the terminal carbons of butadiene and ethene close together to form bonds.
Lowest positive frequency		From the vibration,the reacting centers do not approach each other in the vibration and hence does not lead to the reaction taking place.
Table 3: Vibration of Trasition State.

Reaction Path

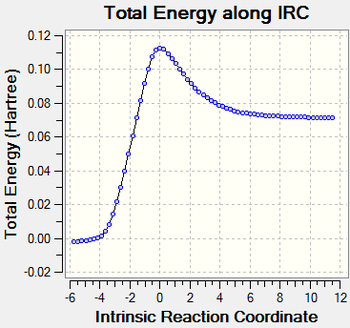
Reaction Path

Formation of Cyclohaxene(IRC)	Energy Curve
Table 4: Reaction path of cyclohexene

The formation of cyclohexene is synchronous because the bond between the reacting centers break at the same time. This can be proved by the presence of a single maximum in the potential energy curve.

Nf710 (talk) 22:57, 14 December 2016 (UTC) Good section however you could have stated if it was normal or invest demand.

Exercise 2

Transition State MO

Molecular Orbitals

Type of Product	MO	Transition State MO
Exo Product	HOMO
Exo Product	Second HOMO
Exo Product	LUMO
Exo Product	Second LUMO
ENDO Product	HOMO
ENDO Product	Second HOMO
ENDO Product	LUMO
ENDO Product	Second LUMO
Table 5: Transition state MO from cyclohexene and 1,3-dioxole.

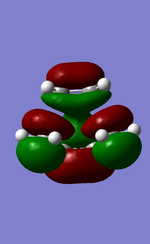
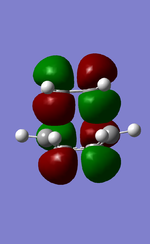
The HOMO and LUMO TS of both exo and endo products are symmetric because they are formed by HOMO of dienophile and LUMO of diene that are also symmetric. Whereas both the LUMO of dienophile(antisymmetric)and HOMO of the diene(antisymmetric) form the second HOMO and second LUMO of the TS which are both antisymmetric. The HOMO of transition state is formed between the HOMO of 1,3-dioxole(dienophile) and the LUMO of hexacyclodiene(diene). From the HOMO TS shown above the orbitals of 1,3-dioxole dominate over the orbitals from hexacyclodiene. This is because 1,3-dioxole has electron donating groups that pulls up the potential energy of the HOMO of 1,3-dioxole. Therefore, this reaction is an inverse electron demand Diels-Alder reaction.

Nf710 (talk) 23:00, 14 December 2016 (UTC) Excellent use of the MOs to come to this conclusion

Thermochemistry

Sum of electronic and thermal Free Energies

	Cyclopentadiene(Hartree)	1,3-dioxole (Hartree)	Reactants (Hartree)	Product (Hatree)	Transition State (Hartree)	Energy Barrier (KJ/mol)	Reaction Energy(KJ/mol)
exo	-233.324377	-267.068644	-500.393021	-500.417324	-500.329164	167.65	63.84
endo	-233.324377	-267.068644	-500.393021	-500.418691	-500.332149	159.82	67.40
(Table 6:Values of the sum of electronic and thermal Free Energies, calculation ran at DFT (B3LYP))

The endo product has a more negative energy than the exo product. Therefore it is more thermodinamically stable compare to the exo product. The energy barrier of the endo product is lower than the exo product. Hence endo product is both kinetically and thermodinamically favourable product.

From table 5, we can see that in the endo HOMO transition state, there are secondary (non-bonding) orbital interactions between the p orbital of oxygens in 1,3-dioxole and the p orbitals in diene. This will lower its energy barrier and make it more kinetically favorable. The exo product only has a primary (bonding) orbital interactions.Besides that, the sp3 carbon centres of both cyclohexene and 1,3-dioxole might have cause some steric hindrance which cause it to be both unfavourable thermodynamically and kinetically. For the endo product, the sp3 carbon centres of the cyclohexene and 1,3-dioxole are pointing at different direction, hence no steric factors that will cause in increased of energy barrier.

Nf710 (talk) 23:05, 14 December 2016 (UTC) Correct energies, very well done section.,

Exercise 3

Intrinsic Reaction Coordinate

Transition State of o-Xylylene-SO2 Cycloaddition

Reaction	Type of Product	Transition state	IRC	Total Energy along IRC
Diels-Alder	Exo
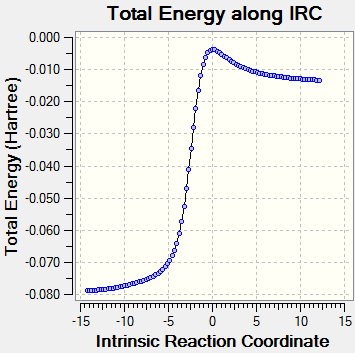
Backward Diels-Alder Path of Exo product.
	Endo
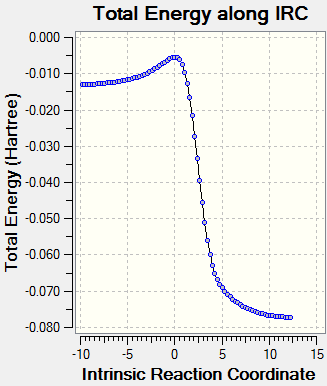
Foward Diels-Alder Path of endo product.
Cheletropic	-
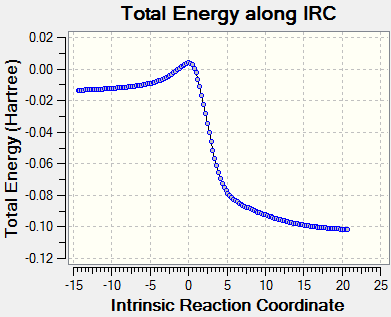
Forward cheletropic reaction
Table 7: Transition state and IRC of Diels-Alder and cheletropic pathway.

Energy Profile

Sum of electronic and thermal Free Energies

	Xylylene(Hartree)	SO2 (Hartree)	Reactants (Hartree)	Product (Hartree)	Transition State (Hartree)	Energy Barrier (KJ/mol)	Reaction Energy(KJ/mol)
exo Diels-Alder	0.178764	-0.119269	0.059495	0.021455	0.092074	101.44	-99.87
endo Diels-Alder	0.178764	-0.119269	0.059495	0.021695	0.090560	81.56	-99.24
Cheletropic	0.178764	-0.119269	0.059495	0.000005	0.099055	103.86	-156.19
(Table 8:Values of the sum of electronic and thermal Free Energies, calculation ran at semi-empirical(PM6))

(Calculation for exo barrier is incorrect Tam10 (talk) 12:21, 6 December 2016 (UTC))

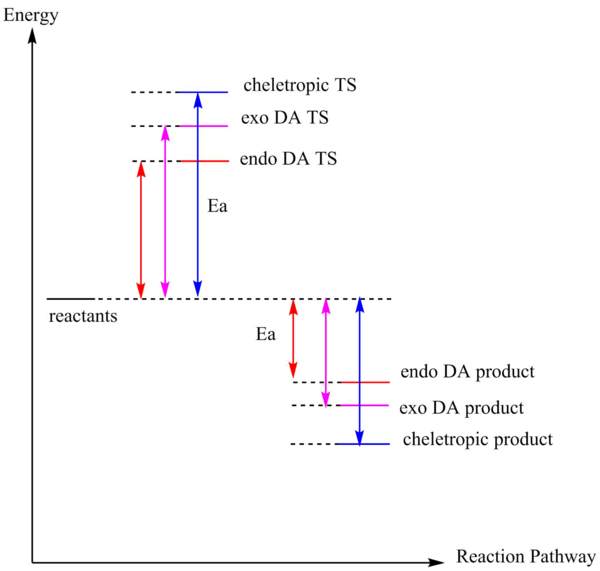
The energy of reactant is calculated by adding both the energy of SO₂ and xylylene. (In vacuum, no interaction between xylylene and SO₂.) Compare to the exo product in exercise 2, there is no steric problem in the exo product. For the diels-Alder pathway, the exo product has a lower energy than the endo product, hence it is the thermodynamically favoured product. The energy barrier(activation energy) of the exo product is higher that the endo product. Therefore, endo product is the kinetically favoured product. Due to small difference between the endo and exo product, and with the secondary interaction between the p orbital of the oxygen in the SO₂ and the p orbital of the diene, the endo product will probably be the major product. Within Diels-Alder product and cheletropic product, the energy barrier of cheletropic product is around 79 kJ/mol higher than the Diels-Alder product but the cheletropic product has a much lower energy than the Diels-Alder product. Hence, the Diels-Alder pathway is more preferred at low temperature and the cheletropic pathway is more preferred at high temperature so that it has enough energy to overcome the high activation energy.

Xylylene is unstable and this can be proven by its high Gibbs free energy. According to the IRC pathway, after the bonding of the 6-membered ring the energy of the product drops. This is due to the formation of delocalised pi system that forms resonance which lowers the energy of the product.

Reaction Profile

Diagram 2: Energy profile between Dielse-Alder pathway and cheletropic pathway.

Diels-Alder Reaction for the second cis-butadiene fragment in o-xylylene

Sum of electronic and thermal Free Energies second cis-butadiene fragment in o-xylylene

	Xylylene(Hartree)	SO2 (Hartree)	Reactants (Hartree)	Product (Hartree)	Transition State (Hartree)	Energy Barrier (KJ/mol)	Reaction Energy(KJ/mol)
exo Diels-Alder	0.178764	-0.119269	0.059495	0.065610	0.102066	111.77	16.05
endo Diels-Alder	0.178764	-0.119269	0.059495	0.067304	0.105053	119.61	20.50
(Table 9:Values of the sum of electronic and thermal Free Energies for second cis-butadiene fragment in o-xylylene, calculation ran at semi-empirical(PM6))

(Not too important here, but it's a good idea to explicitly say the reaction energies are positive to prevent ambiguity Tam10 (talk) 12:17, 6 December 2016 (UTC))

This reaction is endothermic for both endo and exo product. The endo(0.067304 kJ/mol) and exo(0.065610 kJ/mol) products of Diels-Alder Reaction between second cis-butadiene fragment in o-xylylene and SO₂ are unfavourable because both has higher energy than the reactants (0.059495 kJ/mol).

Conclusion

The partly formed C-C bonds in the TS of the reaction between butadiene and ethene is shorter than the Van der Waals radii(3.4 Å). This shows that the reacting carbon from butadiene and ethene are approaching together to form a bond. Along the reaction, all double bond shortens to form single bond and all single bond elongate to form double bond. New bonds are formed between the reacting carbons at the same time for the Diels-Alder reaction between butadiene and ethene, therefore it is a synchronous reaction.

The endo product of the reaction between cyclopentadiene and 1,3-dioxole is kinetically and thermodynamically favoured product because the secondary interaction between the p orbital of oxygen in 1,3-dioxole and p orbital of diene provides extra stability of product in the formation of transition state. The exo product has higher energy than expected due to steric problem caused by the sp3 carbon centres of both cyclohexene and 1,3-dioxole. From the HOMO of TS from table 5, it is clearly dominated by the HOMO of 1,3-dioxole(dienophile). The HOMO and LUMO TS of both exo and endo products are symmetric because they are formed by HOMO of dienophile and LUMO of diene that are also symmetric.

Diels Alder reaction between xylylene and SO₂ will only occur at the outer cis butadiene fragment of the xylylene. The product obtained through the reaction with the second cis-butadiene fragment in o-xylylene is unfavourable because the it has higher energy than the reactant which might due to increase steric hindrance of the product compare to it's reactants.