Rep:Wm1415TransitionStates

This is William Micou's report on the Transition States computational lab, starting Monday 11th December 2017.

Introduction

Transition state analysis is a powerful technique to predict major products and observed stereochemistry; to rationalise reaction rates with different substituents; to examine reaction mechanisms and to understand catalytic cycles. Transition states are very difficult to probe experimentally: here, transition states for a variety of pericyclic reactions will be calculated computationally.

The potential energy surface of a molecule consisting of N atoms exists in (3N-6) dimensions. The potential energy can be expressed as a function of (3N-6) independent nuclear coordinates, $q_i$:

$E=f(q_1,q_2,...,q_{3N-6})$

A stable structure sits in a local minimum on the potential energy surface, whereas a transition state is a saddle point on the PES. These are both stationary points, where:

$\frac{\partial E(q_i)}{\partial q_i}=0$ along every coordinate $q_i$.

Minima and transition states can be distinguished by their second derivatives. At a minimum, the energy must increase in all directions from that point on the PES: therefore,

$\frac{{\partial }^{2}E}{\partial q_i^2}>0$ for all $q_i$.

At a transition state, the energy increases in all directions except one: the energy decreases along the reaction path. A transition state is hence defined as a stationary point on the PES with one negative Hessian eigenvalue.^[1]

The second derivatives of the PES correspond to the force constants of the vibrations along the chosen nuclear coordinates:

$k=\frac{{\partial }^{2}E}{\partial q^2}$, with the frequency of the vibration $\omega =\frac{1}{2\pi }\sqrt{\frac{k}{\mu }}$

Therefore, a transition state will have an optimised structure with a single imaginary frequency - this corresponds to the collective motions of the atoms forming the products and lowering the energy. In contrast, optimised reactants or products which sit at a local minimum have only positive frequency vibrations.

Nf710 (talk) 12:07, 16 January 2018 (UTC) This is excellently written and you have clearly understood how the hessian matrix is used. Well done. Nice use of the equations to make it clear.

Methodology

Calculations were executed with Gaussian 09, Revision D.01, with input files prepared in GaussView 5.0.9. Transition states were located and reaction paths calculated using the following sequence:

• Products optimised at the desired level of approximation.
• Bonds formed in the reaction are broken and these bond lengths are frozen to around 2.2 Å for C-C bonds, 2.0 Å for C-O and 2.4 Å for C-S bonds. The structure is reoptimised.
• Bonds are unfrozen and the transition state is located using the Berny algorithm, calculating the force constants only once.
• The transition state structure is checked with an IRC (intrinsic reaction coordinate) calculation at the PM6 level (as more accurate calculations are computationally expensive) and a frequency calculation.

The B3LYP level of approximation makes use of Density Functional Theory (DFT)^[2]. The electron energy is a functional^[3] of the electronic density, $E[\rho ]$. The B3LYP force field is a hybrid density functional method^[3], incorporating the exchange correlation predicted by gradient-corrected functionals^[2] (GGA methods - Generalised Gradient Approximation) along with exact, Hartree-Fock exchange^[2]. These calculations are considerably heavier and time allowed for B3LYP calculations in Exercise 2 only.

The PM6 approximation is a semi-empirical model: reference data is used^[4] in combination with calculations based on a Hartree-Fock model (with considerable simplifications). These calculations are fast and successful for reasonably small molecules, although the PM6 method has been modified to model proteins^[5].

Nf710 (talk) 12:13, 16 January 2018 (UTC) I would be careful calling B3LYP a force field method as this would imply a molecular mechanics method. But good understanding on the exchange correlation correction. PM6 is correct, the integrals are replaces by some experimentally fitted parameters,

Exercise 1: Butadiene + Ethene Diels-Alder Reaction

Optimised structures of the reactants and transition state (PM6 level)

The table below contains Jmol applets of the reactants and transition state structures optimised at the PM6 level.

Ethene	Butadiene (s-cis)	Transition state

Confirmation of Transition State

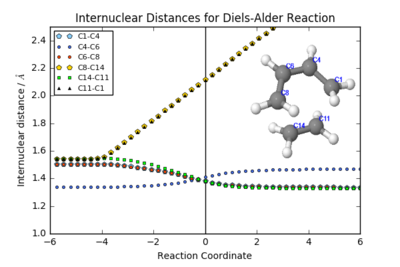
The frequency calculation on the TS structure yielded an imaginary vibration at -948 cm^-1: this corresponds to the motion of atoms that leads to the formation of products. Further evidence for a correct TS was obtained through an IRC calculation: this structure is indeed the maximum along the minimum energy path. The table below provides a plot of the C-C bond lengths during the reaction; an animation of the reaction calculated reaction path; and a plot of the energy, along with its derivative, against the reaction coordinate. It is worth noting that in this case, the IRC path was arbitrarily calculated from the products to the reactants: hence the reversed animation. The same atom labels were used as in the Jmol structures above.

Internuclear distances in IRC path	Diels-Alder Reaction Animation	IRC Path Energy Plot

The animation shows that this Diels-Alder reaction is synchronous: the new σ bonds (C8-C14 and C11-C1) are formed at the same time. These bond lengths are identical in the internuclear distances plot, which also show shortening of the C4-C6 bond as it becomes a double bond (around 1.35 Å). Also shown is the lengthening of the 3 double bonds involved in the cycloaddition, which all become single bonds (C14-C11, C1-C4 and C6-C8) with lengths of between 1.50-1.54 Å (C1-C4 and C6-C8, which are adjacent to the double bond in the product, are slightly shorter). Carbon has a van der Waals radius of 1.70 Å.

In the transition state, the C8-C14/C11-C1 bonds measure around 2.12 Å - the new σ bonds are not yet fully formed, but well within twice the van der Waals radius. The original double bonds are all elongated - around 1.38 Å, and the originally singly-bonded C4-C6 is shorted to 1.41 Å.

Optimisation and Analysis of Product

To reduce the number of Jmol applets on this page, these structures have not been embedded - they can be opened in a new window by clicking the following links. A PM6-level optimisation of the products of the IRC yields boat cyclohexene: this was compared to a PM6-level optimisation of chair cyclohexene. The boat structure features an imaginary frequency: this corresponds to the collective motion of atoms that would yield the chair cyclohexene structure, lowering the energy.

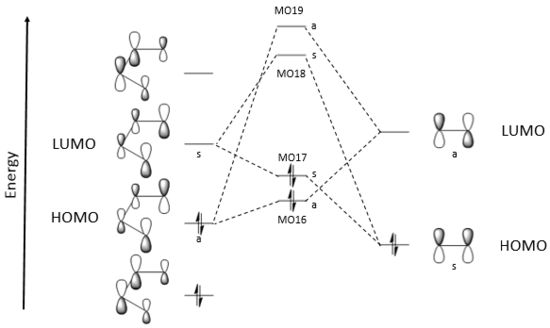
Orbital Description of the Diels-Alder Reaction

(Fv611 (talk) Very confused on why you didn't draw the TS LUMO and LUMO+1 according to the calculated relative energies: you know the order is (by decreasing energy) MO13 - ethene LUMO - TS LUMO+1 - butadiene LUMO - TS LUMO, so why not draw them this way?)

MO Diagram showing the orbitals involved in the Diels-Alder reaction. While the ordering of the energies of the reactant frontier orbitals has been respected, the diagram is not drawn to scale and the transition state energy levels are skewed for clarity. Approximate energy levels calculated at the PM6-level approximation are listed in the table opposite.

Ethene Energy / a.u. Butadiene Energy / a.u. Transition State Energy / a.u. MO 13 0.0636 MO 19 0.0307 LUMO 0.0426 LUMO 0.0194 MO 18 0.0173 HOMO -0.3923 HOMO -0.3590 MO 17 -0.3253 MO 10 -0.4133 MO 16 -0.3276 LUMOdienophile - HOMOdiene = 0.4016 a.u. LUMOdiene - HOMOdienophile = 0.4117 a.u. The smallest energy gap is that between the LUMO of ethene and the HOMO of butadiene (the antisymmetric orbitals). The interaction between these orbitals is stronger as there is greater orbital overlap: the reaction proceeds by electrons from the HOMO of the diene populating the LUMO of the dienophile (MO 16) - normal electron demand. The other bonding orbital in the TS, MO 17, is formed from the interaction between the HOMO of ethene and the LUMO of butadiene.

The orbital overlap integral is non-zero for symmetric-symmetric and antisymmetric-antisymmetric orbital interactions; but the orbital overlap integral is zero for symmetric-antisymmetric interactions. (Fv611 (talk) You are missing the final part of this reasoning: this is why only S-S and AS-AS orbital interactions are allowed.)

The Woodward-Hoffmann rules can be used to predict whether a pericyclic reaction is allowed by symmetry. According to the Woodward-Hoffman rules, a cycloaddition is thermally allowed if the total number of (4q+2)_s and (4r)_a components is odd^[6]. Here, the 's' label refers to a suprafacial component, which forms new bonds on the same side at both ends ('a' label - antarafacial, opposite sides). The Diels-Alder reaction is a [_π4_s+_π2_s] cycloaddition: (4q+2)_s + (4r)_a = 1, so it is allowed.

Exercise 2

Optimised Reactants: B3LYP/6-31G(d)

These Jmol files have been excluded from this page to speed up loading time. The applets can be accessed here: cyclohexadiene and 1,3-dioxole. There are no negative frequencies as these are stable structures.

Endo/Exo Transition States and Products: B3LYP/6-31G(d)

Endo TS	Endo Product	Exo TS	Exo Product

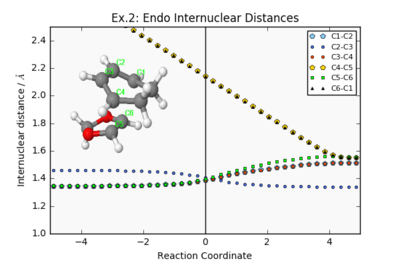
Endo/Exo IRC Paths (PM6 Level)

Endo Internuclear distances	Endo Reaction Animation	Endo IRC Energy Plot
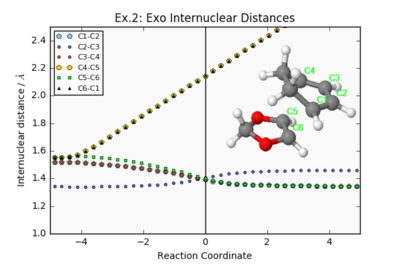
Exo Internuclear distances	Exo Reaction Animation	Exo IRC Energy Plot

MO Diagram: Diels-Alder Inverse Electron Demand

(Fv611 (talk) As before, even though you state that you are respecting the order of your calculated energies, you are not. The highest energy interacting orbital is the dioxole LUMO, not the TS LUMO +1 (which by the way has an energy of +0.0154, not -0.0154). Additionally, you make no comment on the difference in terms of relative energies between the exo and endo cases.)

MO Diagram showing the FMOs. While the ordering of the energies of the reactant FMOs has been respected, the diagram is not drawn to scale and the transition state energy levels are skewed for clarity. Approximate energy levels calculated at the B3LYP 6-31G(d)-level approximation are listed in the table opposite.

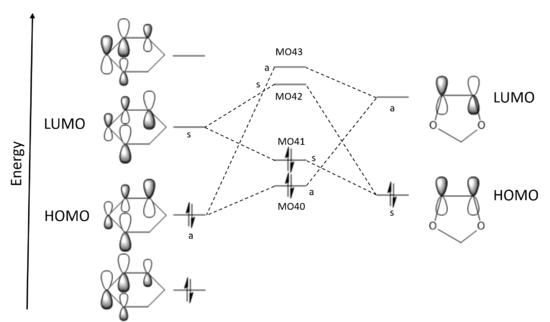1,3-dioxole Energy / a.u. Cyclohexadiene Energy / a.u. Endo TS Energy / a.u. MO 24 0.0874 MO 43 -0.0154 LUMO 0.0380 LUMO -0.0171 MO 42 -0.0046 HOMO -0.1959 HOMO -0.2055 MO 41 -0.1905 MO 21 -0.2994 MO 40 -0.1965 LUMOdienophile - HOMOdiene = 0.2435 a.u. LUMOdiene - HOMOdienophile = 0.1788 a.u. In this case, it is the energy gap between the LUMO of the diene and the HOMO of the dienophile that is smallest and leads to the greatest orbital overlap. The dienophile, 1,3-dioxole, is electron-rich: electrons flow from its HOMO to the diene LUMO - this is inverse electron demand. This interaction can be visualised as MO 41 in both the endo and exo transition states. Interactions between the dienophile LUMO and diene HOMO form MO 40 in the transition state.

Because the energies of the interacting orbitals are a better match than in the butadiene and ethene reaction, there is greater orbital overlap and hence greater stabilisation of the transition state: the reaction with the electron-rich 1,3-dioxole would be much faster.

Energy Profile: Secondary Orbital Interactions

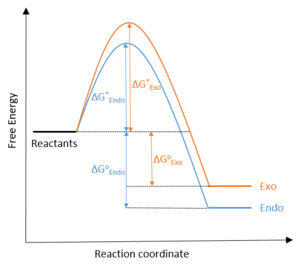
The endo product is both the kinetic and thermodynamic product of the reaction: it is formed from a lower energy TS (difference of 8 kJ/mol) and releases more energy (difference of 3.6 kJ/mol) in the reaction. The exo product is comparatively destabilised because of the unfavourable steric clash between the heteroatomic 5-membered ring and the bridging ethyl group across the newly-formed 6-membered ring from the Diels-Alder reaction. The endo transition state is stabilised by secondary orbital interactions (SOI)[7]. These interactions come about between atomic orbitals that are not involved in the formation or cleavage of σ bonds[7]. In the endo TS, the O atoms are aligned with the back of the diene. While this configuration is sterically unfavourable, it allows for the SOI between the O lone pairs and the orbitals at the back end of the diene LUMO. This is a favourable interaction which is only accessible to the endo TS, and more than makes up for the increased steric clash - resulting in a lower energy transition state. These interactions can be clearly seen in the Jmol files above: select MO 41 in the transition state structures (and adjusting the MO cutoff value if necessary).

Free energies / kJ/mol $\mathrm{\Delta }{G}_{endo}^o$ -67.4 $\mathrm{\Delta }{G}_{exo}^o$ -63.8 $\mathrm{\Delta }{G}_{endo}^{*}$ 160 $\mathrm{\Delta }{G}_{exo}^{*}$ 168

Back to Introduction.

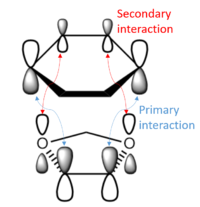
Nf710 (talk) 12:21, 16 January 2018 (UTC) Your energies are correct well done. And your JMols ae very very nicely done. It is clear and concise too. When you are comparing the energies of the MOs of the different reactants you need to be careful here. This is because they are on different potential energy surfaces and hence the relative energies are different as the Hamiltonian has different amounts of terms in. To do this properly you would do an energy calculation at the last point of the reactants on the IRC and then look at the relative ordering of the MOs there with both reactants on the potential energy surface.

Exercise 3

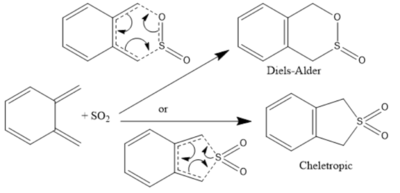
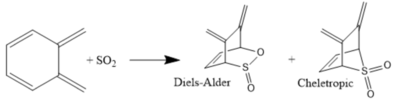
The Reaction between SO₂ and Xylylene

Sulfur dioxide can undergo Diels-Alder and Cheletropic pericyclic reactions with dienes. Xylylene contains two diene fragments: what will be deemed the main fragment undergoes aromatisation in the considered reactions. The following sections contain calculations for the formation of the each of the possible products for both the main and second fragments of xylylene: from these calculations, a reaction profile will be constructed.

Jmol applets for PM6-optimised structures of xylylene and sulfur dioxide have been excluded from the report, but can be opened in a new window from these links.

Main Fragment: Optimised TS (PM6-level) and IRC Paths

Endo TS	Exo TS	Cheletropic TS
Endo IRC Path	Exo IRC Path	Cheletropic IRC Path
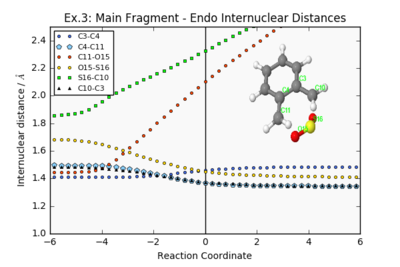
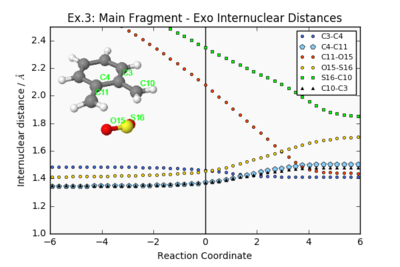
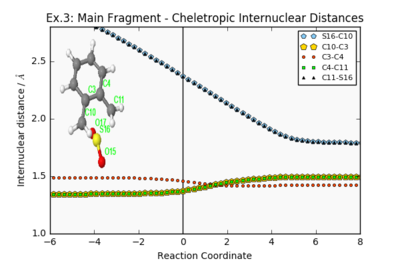
Endo Internuclear Distances	Exo Internuclear Distances	Cheletropic Internuclear Distances
Endo Product Jmol	Exo Product Jmol	Cheletropic Product Jmol

(Very nice JMol scripting and Python. Try to be consistent with respect to the direction along the IRC Tam10 (talk) 16:00, 9 January 2018 (UTC))

Second Fragment: Optimised TS (PM6-level) and IRC Paths

Endo TS	Exo TS	Cheletropic TS
Endo IRC Path	Exo IRC Path	Cheletropic IRC Path
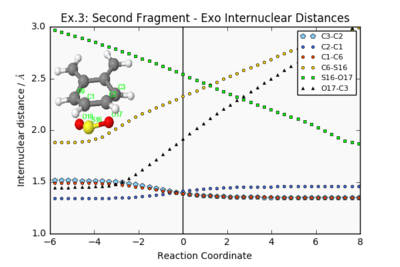
Endo Internuclear Distances	Exo Internuclear Distances	Cheletropic Internuclear Distances
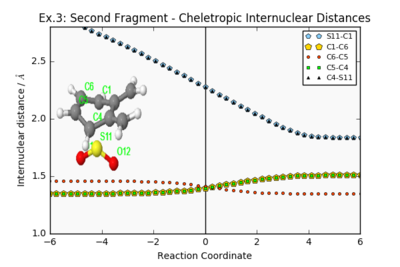Endo Product Jmol	Exo Product Jmol	Cheletropic Product Jmol

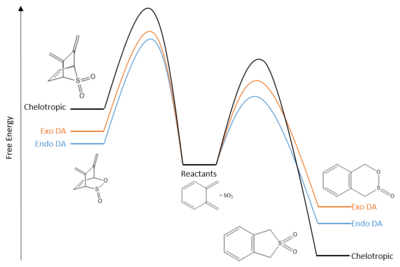
Reaction Profile

Main Fragment: Free energies / kJ/mol $\mathrm{\Delta }{G}_{endo}^o$ -99.2 $\mathrm{\Delta }{G}_{exo}^o$ -84.1 $\mathrm{\Delta }{G}_{chel}^o$ -156 $\mathrm{\Delta }{G}_{endo}^{*}$ 81.6 $\mathrm{\Delta }{G}_{exo}^{*}$ 85.6 $\mathrm{\Delta }{G}_{chel}^{*}$ 104 Second Fragment: Free energies / kJ/mol $\mathrm{\Delta }{G}_{endo}^o$ 16.1 $\mathrm{\Delta }{G}_{exo}^o$ 20.6 $\mathrm{\Delta }{G}_{chel}^o$ 47.1 $\mathrm{\Delta }{G}_{endo}^{*}$ 112 $\mathrm{\Delta }{G}_{exo}^{*}$ 120 $\mathrm{\Delta }{G}_{chel}^{*}$ 141

(Use straight lines for reaction profiles Tam10 (talk) 16:00, 9 January 2018 (UTC))

Reaction with the second fragment are clearly very thermodynamically and kinetically unfavourable: the overall reactions are endothermic, and all activation energies are larger than in reactions with the main fragment. The products from these theoretical reactions would not be observed experimentally.

Reaction with the main fragment is much more favourable on account of the formation of the benzene ring. The aromatisation confers stability to both the products and the transition states. The cheletropic reaction yields the thermodynamic product, which contains the more stable 5-membered ring and an additional strong S=O bond. However, the chelotropic rearrangement proceeds via a considerably higher reaction barrier, and at very low temperatures one might observe the kinetic product: the endo Diels-Alder product. The endo configuration has a stabilised TS due to secondary orbital interactions, as discussed previously. Endo-selectivity for this Diels-Alder reaction is reported by the literature^[8].

The reaction between xylylene and SO₂ has been performed in the literature^[8]. At 20 ^oC, SO₂ adds reversibly and a 1:9 mixture of the Diels-Alder and cheletropic products was obtained. Low temperatures are required for the reaction to proceed, because of the reduction in entropy as SO₂ gas is consumed. Prior simulations of this reaction have included a second molecule of SO₂ that may help stabilise the Diels-Alder transition state^[9].

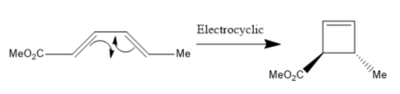
Extension: 4π Electrocyclic Ring Closure with Conrotation (PM6-Level)

According to the Woodward-Hoffmann rules, an electrocyclic reaction involving 4n π electrons should proceed via a conrotary mechanism^[6]. The subject of this extension is to demonstrate this stereospecifity, using the same methods as previously in this experiment:

Electrocyclic TS	IRC Path Animation	IRC Energy Plot

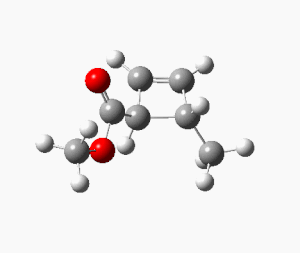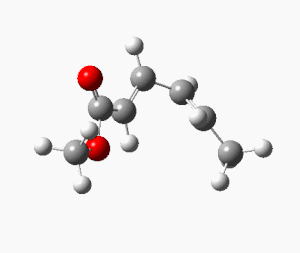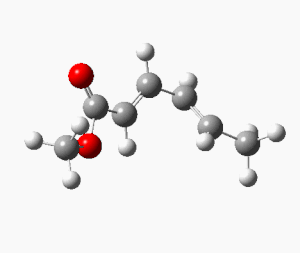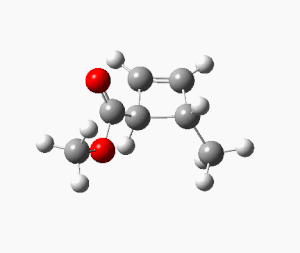
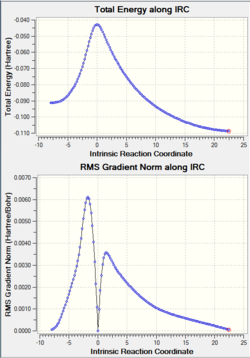
The calculated IRC path clearly shows the conrotation about the migrating carbon atoms, confirming the predicted stereochemistry of the products.

(Good additional section. What would happen on the excited state? Tam10 (talk) 16:04, 9 January 2018 (UTC))

(+6%)

Conclusion

In this experiment, the transition states were successfully calculated for a variety of pericyclic reactions, using both the semi-empirical PM6 and the DFT B3LYP 6-31G(d) levels of approximation. The results agreed with predictions laid out by the Woodward-Hoffmann rules. The Diels-Alder reaction between butadiene and ethene was found to proceed via normal electron demand; using an electron-rich dienophile, 1,3-dioxole, resulted in inverse electron demand. In the reaction between 1,3-dioxole and cyclohexadiene, the endo product was found to be both the kinetic and thermodynamic product: the endo transition state is stabilised by secondary orbital interactions, and the exo product is destabilised by unfavourable steric clashes.

The rearomatisation was confirmed to be the driving force for the pericyclic reactions of SO₂ with xylylene, as reactions with the second diene fragment yielded kinetically and thermodynamically very unfavourable products. The thermodynamic product arises from the cheletropic mechanism, but the kinetic product arises from the faster, reversible Diels-Alder cycloaddition - this finding was backed up with experimental observations from literature^[8].

The Woodward-Hoffmann rules were further investigated: the predicted stereochemistry of the 4π electrocyclic reaction was obtained from these theoretical calculations.

References

1 D. Wales, in Energy Landscapes: Applications to Clusters, Biomolecules and Glasses, Cambridge University Press, 2004, pp. 192–240.

2 P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.

3 S. F. Sousa, P. A. Fernandes and M. J. Ramos, J. Phys. Chem. A, 2007, 111, 10439–10452.

4 J. J. P. Stewart, J. Mol. Model., 2007, 13, 1173–1213.

5 J. J. P. Stewart, J. Mol. Model., 2009, 15, 765–805.

6 R. B. Woodward and R. Hoffmann, Angew. Chemie Int. Ed. English, 1969, 8, 781–853.

7 A. Arrieta, F. P. Cossío and B. Lecea, J. Org. Chem., 2001, 66, 6178–6180.

8 B. Deguin and P. Vogel, J. Am. Chem. Soc., 1992, 114, 9210–9211.

9 T. Fernandez, J. A. Sordo, F. Monnat, B. Deguin and P. Vogel, J. Am. Chem. Soc., 1998, 120, 13276–13277.