Rep:Winston
Physical Computational Laboratory
Cope Rearrangement
Introduction
Proposed transition structures for the [3,3] Cope Rearrangement of 1,5-hexadiene has been the topic of debate by theoriticians for an extensive period of time. Initially three transition states for the reaction were proposed, however the Bis-Allyl mechanism was dismissed on experimental grounds. Thus two mechanisms for the reaction pathway remained open for discussion, one involving the concerted sigma bond shift aromatic transition state and the other being the formation of a stable 1,4-Diyl diradical intermediate[1]:
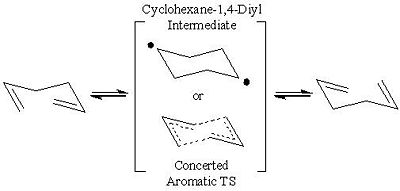
Computational chemistry was used to investigate this further, and it was found that the transition states concluded from calculations largely depended upon the methods employed. Such that semi-empirical methods supported the Diyl pathway and DFT quantum mechanical methods supported the concerted aromatic transition state.
In this investigation the density functional theory was used with B3LYP/6-31G method and basis sets. Activation and enthalpy energies for the 'boat' and 'chair' confomers were then analysed.
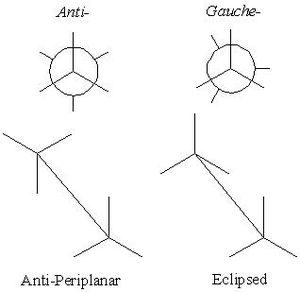
1,5-hexadiene exists in various forms, they can be classified as either anti- (roughly anti-periplanar) or gauche- (roughly eclipsed) based upon the orientation of the molecule about the central carbon atoms (C3 and C4).
Prior to calculation using the DFT/6-31G method, various confomers of 1,5-hexadiene were optimised using the less complex HF/3-21G method. This enabled quicker and more accurate calculation by the DFT method since the optimisations were almost step-wise in complexity.
Optimising 1,5-hexadiene
1,5-hexadiene structures were optimised in Gaussian using a HF/3-21G method and values for the energies were compared to that of literature:
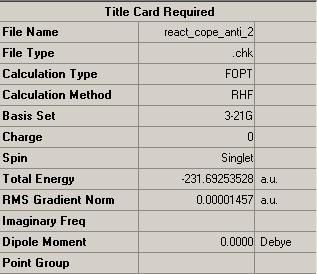 |
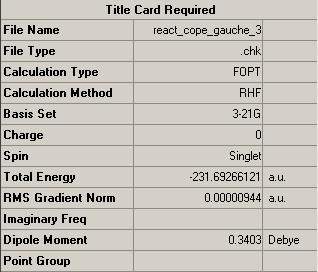 |
Summary of the results from the optimisation calculations could be obtained from gaussian. From the tables it can be deduced that the HF/3-21G minimised energy for anti-2 hexadiene is -231.69254 a.u. and for gauche-3 hexadiene it is -231.69266. These energies are consistent with that of the values given in the appendix. Where 1 Hartree a.u. is equivalent to 627.50947 kcal/mol[2]. Thus, it can be concluded that the gauche 1,5-hexadiene conformation is thermodynamically more stable than that of the anti 1,5-hexadiene conformation by 0.0753 kcal/mol.
This is unexpected, since basic theory would suggest that the anti confomer shows greater stability, as it is less sterically strained. Dipole moments for the confomers also indicate that the anti molecule should exhibit greater stability. However, one reason that could be used to explain why the gauche conformation is preffered, is due to possible pi-overlap between the two pi-systems. As the gauche conformation enables the pi-systems to be orientated close to each other, this factor could in fact play a major role in stabilisation and thus overcome all the other factors which favour the anti conformation.
Symmetry point groups of the molecules were deduced by Gaussian, these were found to be Ci for the anti-2 hexadiene and C1 for the gauche-3 hexadiene. Again, these properties were consistent with those in the appendix.
Optimisation of the anti-2 hexadiene was increased to the B3LYP/6-31G method. Given the increased complexity of this calculation method, it is expected that values for energies differ such that a more stable conformation is provided by the B3LYP/6-31G method.
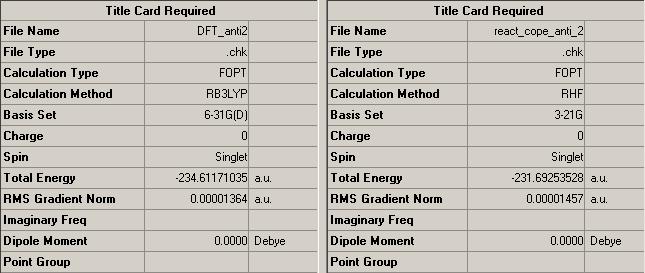
As expected the energy for the B3LYP/6-31G method provides a significantly better minimum for the anti-2 hexadiene {(https://www.ch.imperial.ac.uk/wiki/images/e/ea/REACT_COPE_ANTI_2_DFT.LOG )}. The calculation provides a structure that is 1831.81 kcal/mol more stable than the previous HF/3-21G method.
The geometry of the molecule remains the same, such that both calculations produce a structure that has a Ci symmetry point group. This indicates that the energy difference is largely down to manipulation of bond lengths rather than modification of bond angles and overall geometry.
Further detailed analysis of the bond lengths in each of the molecules supports this assumption: HF/3-21G anti-2 1,5-hexadiene - (C1 to C2/C5 to C6) pi-bond length = 1.316Ǻ, (C3 to C4) sigma-bond length = 1.552Ǻ. B3LYP/6-31G anti-2 1,5-hexadiene - (C1 to C2/C5 to C6) pi-bond length = 1.333Ǻ, (C3 to C4) sigma-bond length = 1.548Ǻ. Typical Alkene (C=C)bond length = 1.33Ǻ, and typical (C-C) bond length = 1.54Ǻ.
Thus, it is ability of the B3LYP/6-31G method to more accurately predict the length of the C=C bond within the molecule which results in a more stable geometry.
Frequency analysis of the anti-2 1,5-hexadiene was then conducted in order to determine the calculation had reached a minimum value, this was confirmed by the presence of fully positive vibrational frequencies. - Since the frequency calculation is essentially a second derivative of the potential energy curve for optimisation, subsequently a minima is indicated by positive values.

| Bond Type | Frequency (cm-1) | Lit.[3] Frequency (cm-1) |
|---|---|---|
| =CH2 (bend) | 940 | 880-995 |
| C=C (asymmetric stretch) | 1734 | 1900-200 |
| CH2 (alkane) | 3031,3080 | 2850-3000 |
Tabulated frequencies for the molecule was formed by analysis of the animated frequencies, these values were then compared to that of literature. It can be noted that the frequencies for the B3LYP/6-31G are consistent to that of literture, thus reinforcing the use of this method.
By examination of the .log file for the frequency calculation, the sum of electronic and zero-point energies, the sum of electronic and thermal energies, the sum of electronic and thermal enthalpies, and the sum of electronic and thermal free energies could be determined:
sum of electronic and zero-point energies = -234.469204 a.u. sum of electronic and thermal energies = -234.461857 a.u. sum of electronic and thermal enthalpies = -234.460913 a.u. sum of electronic and thermal free energies = -234.500777 a.u.
Optimising the Chair Transition Structure
Both chair and boat transition states can exist during the Cope rearrangement. The chair transition structure consists of two C3H5 allyl fragments positioned 2.2Ǻ apart with a symmetry point group of C2h, and the boat transisiotn structure consists of the same allyl fragments positioned 2.2Ǻ apart with a different symmetry point group of C2v.
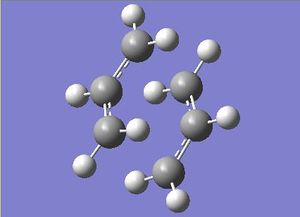
Given the properties associated with both of the transition structures, it seemed feasible to first optimise the basic fragment that is common in both structures. Thus, prior to further investigation into the overall optimisation of the full transition states, the HF/3-21G method was used to optimise the allyl fragment (CH2CHCH2). Once optimised, this was copied and pasted such that two fragments could be orientated about each other to vaguely represent the chair transisiton state - (terminal carbons were positioned 2.2Ǻ apart).
This guess provided a viable basis structure that could be optimised further and used to analyse the chair transisiton structure for the Cope rearrangement. Transition state optimisation calculations require a guess structure that is as close as possible to the proposed structure, such that Hessian calculations performed throughout the optimisaton follow that of the true optimistion PES curve.
HF/3-21G method was used to provide an optmisation and frequency analysis of the guess Transition state, the key words opt=noeigen were inserted in order to prevent the calculation aborting if more than one imaginary frequency was detected.This occurs when the guess structure is not close enough to that of the real transition structure. - (Force constants were calculated once throughout the optimisation.)


Results for the HF/3-21G Optimisation and Frequency analysis of the Chair transisiton structure are summarised in the Table (https://www.ch.imperial.ac.uk/wiki/images/e/e6/CHAIR_TS_OPT%2BFREQ.LOG }. It can be noted that the energy for the transition state is 45.94kcal/mol higher than that of the reactant - (anti-2 1,5-hexadiene). This is consistent with theory, and is known as the activation energy for the reaction.
Completion of a successful calculation leads to the presence of one imaginary vibration in the frequency analysis. This has a value of -818cm-1. The vibration is shown below:
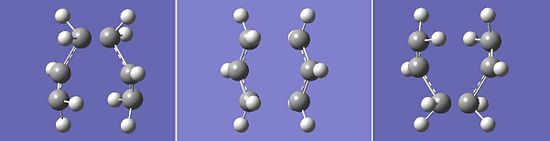
This vibration is consistent with that for the proposed aromatic mechanism of the Cope rearrangement, whereby there is a concerted sigma bond shift between C1,C6 and C3,C4 in the reactant.
Although this calculation proved successful, and subsequently it can be deduced the guess structure was close enough to that of the real transition structure for accurate hessian calculations, extra steps can be encorporated to provide a more precise and therefore reliable calculation. It is knwon as the frozen co-ordinate method. Whereby the reaction coordinate is frozen, the molecule is then optimised and once the molecule is fully relaxed, the reaction coordinate can then be unfrozen and a transition state optimisation performed.
The additional key words of opt=modredundant were needed for this calculation to proceed.
First the guess structure was optimsed to a minimum, using the HF/3-21G method, with a fixed (frozen) bond length of 2.2Ǻ between the two allyl fragments. The next stage is to run a transition state optimisation of the structure with the distance between the two allyl fragments unfrozen. Force constant were not calculated in the optimisation, instead a normal guess Hessian was used:
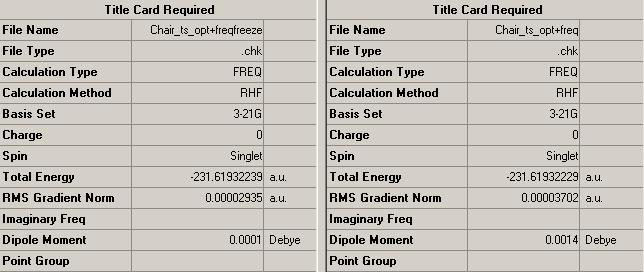
A comparison between the HF/3-21G Optimisation and Frequency analysis for the normal and frozen methods is shown in the table on the left. It is clear to see that the energy difference between the two structures is negligible, therefore suggesting that the initial HF/3-21G method with one force constant calculation was more than satisfactory.
Comparison of bond lengths between the two transition structures also supports the use of the HF/3-21G calculation without frozen parameters, since all exhibit roughly the same value - differences are negligible.
As for the previous calculation, the vibrations of the molecule were analysed (https://www.ch.imperial.ac.uk/wiki/images/9/9c/CHAIR_TS_OPT%2BFREQ%2CFREEZE.LOG). This showed one imaginery vibration (as expected) corresponding to the aromatic concerted sigma-tropic rearrangement, the frequency of this vibration was at -818cm-1.
Optimising the Boat Transition Structure
When caculating the boat transition structure, the QST2 method was used upon the anti-2 1,5-hexadiene. This required a reactant and product molecule to be constructed, as the calculation interpolates between the two structures to find the optimum transition structure for the reaction.
Thus the first stage was to construct both the product and reactant such that they were numbered as follows:
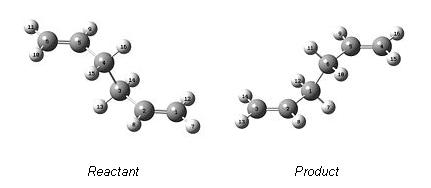
Numbering of molecules in such a way was critical for the successful outcome of the calculation. QTS2 Transition optimisation and frquency analysis was then carried out, and this was found to fail.
Reasons for this failed calculation arise from the geometry of the reactant. The C2h anti-2 geometry adopted by the reatant is clearly far from that of the boat transition structure, thus the calculation cannot cleary see how best to optimise/ rearrange the molecules in a sigma tropic rearrangemnt such that the aromatic boat transition structure is formed.
Alterations to the reactant clearly had to be made such that the calculation method would form and optimise the boat transition structure. This was achieved by orientating the C3,C4 sigma bond into an eclipsed form - (C2,C3,C4,C5 dihedral angle of 0 degrees), by doing so this orientated C1 and C6 closer together, much like in the diagrammatic reaction mechanism shown previously. Furthermore, the C1,C2,C3 and C4,C5,C6 bond angles were altered to 100 degrees:
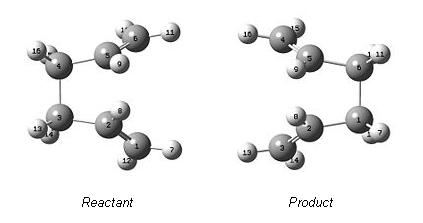
As before, the two molecules were subjected to a QTS2 transition optimisation and frequency analysis. As expected the alterations that were made to both the product and reactant resulted in a successful calculation.

Comparison of the 3-21G level calculations for the chair and boat transition states shows that the chair structure is more energetically favourable. With an energy difference of 10.37 kcal/mol between the two structures.
Previous calculations showed that the 3-21G activation energy for the Cope rearrangement with the Chair transition state was 45.94kcal/mol, therefore it can be concluded that the 3-21G activation energy for the Cope rearrangement with the Boat transition state is 56.31 kcal/mol.
Intrinsic Reaction Coordinate Method for Chair Transition State
IRC can be used to follow the minimum energy path from a transition state down to its minimum on a PES. To investigate this further the chair transition structure calculated not using the frozen co-ordinate method was used. The number of points along the IRC optimisation and frequency analysis was changed from its default setting of 6 to a more thorough 50:
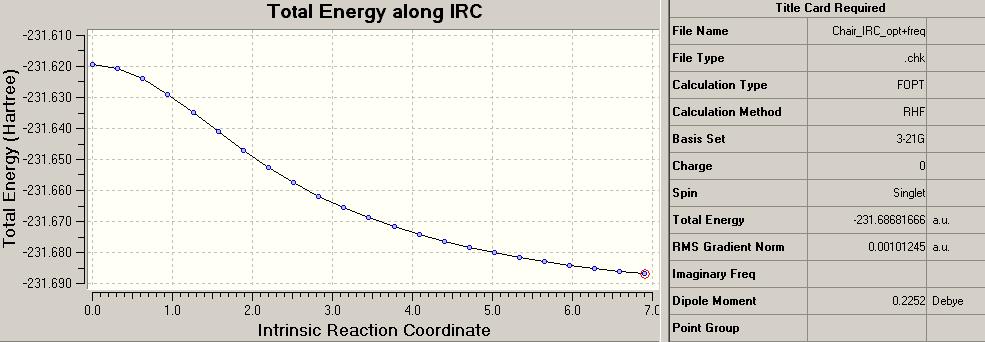
The summary attatched to the IRC plot shows the data associated with the minima point of the calculation with 50 points. In order to determine whether the PES had infact come to a local minima, other comparisons were made. First of which was to increase the number of points in the IRC to 100. This did not alter the minima obtained and the IRC plots were exactly the same. Next came a standard minimisation calculation, this resulted in a local minima structure with 3.04 kcal/mol less energy than that of the IRC 50/100 plots:

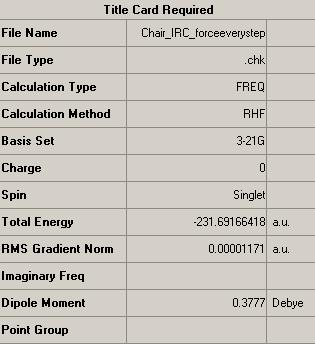
Next came the most reliable and expensive method of locating the minima of the PES curve, this involved computing the force constants at every step along the IRC optimisation and frequency analysis.
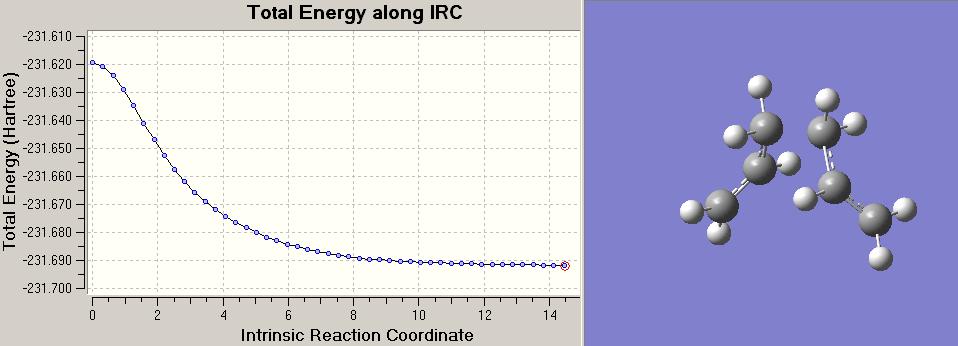
However, this method provided a local minima structure with energy negligibly higher than that of the standard minimisation calculation. Suggesting the minimisation calculation has over compensated in areas.
Optimisation Using B3LYP/6-31G* and Comparisons
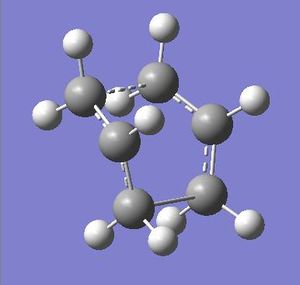
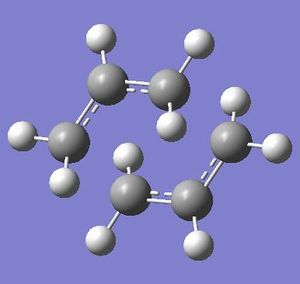
Structures for the Boat and Chair transition staes were subject to more complex optimisation using the B3LYP/6-31G* method. This provided more accurate representation for the structures and data from these calculation could then be compared to that of literature.
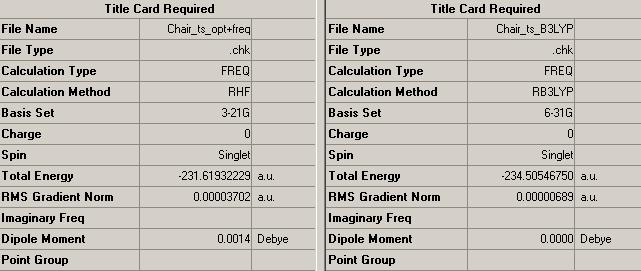
Cleary the B3LYP/6-31G* method provides far greater accuracy and from the previuos calculation used to optimise the reactant (anti-2 1,5-hexadiene) at B3LYP/6-31G* method, the activation energies for the reactions can be decided.
Activation Energy for Boat transition structure = 74.55 kcal/mol
Activation energy for Chair transition structure = 66.67 kcal/mol
Energy difference between transition structures = 7.88 kcal/mol
The Diels Alder Cycloaddition
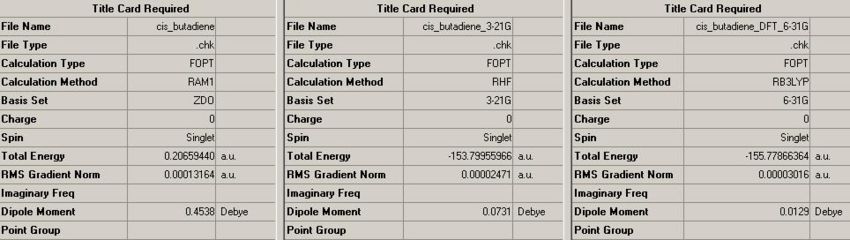
The [4+2] cycloaddition reaction of cis-butadiene with ethene was studied. To do this, cis-butadiene was initially optmiised using the AM1 semi-empirical method of analysis, this was compared to analysis of increasing colpexity. Energies and bond angles were compared.
By analysis of the summary of results for the optimisation, it is evident that solutions for optimisation become progressively more accurate as the method is changed from semi-empirical AM1 to the quantum mechanical B3LYP/6-31G. It can also be noted that the largest difference in energy is experienced from changing the semi-empirical calcultion to the quantum mechanical approach, after which the energy difference is relatively minimal.
| C=C Bond Length | C-C Bond Length | < C=C-C (degrees) | |
|---|---|---|---|
| Semi-Empirical AM1 | 1.39 | 1.36 | 128.12 |
| Quantum Mechanical 6-31G | 1.43 | 1.40 | 134.33 |
| Literature | 1.35 | 1.47 | 124.4 |
Suprisingly the literature values for the bond lengths and angles are not biased toward the more complex quantum mechanical calculation, but instead the bond lengths and angles sway between both methods. Suggesting the moethods do not cater for other forces such as conjugation which effect the structure.
During a diels-alder reaction the HOMO/LUMO are involved depending upon which type of mechanism the reaction follows. This depends upon the reaction being following the inverse electron demand are normal electron demand. Given this, the MO for the HOMO and LUMO of cis-butadiene were investigated and symmetry with respect to the plane determined.
| LUMO | HOMO | Symmetry with respect to plane | |
|---|---|---|---|
| Semi-Empirical AM1 | 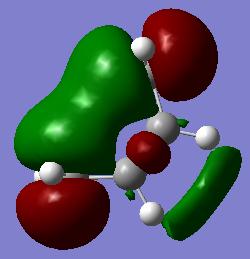
|
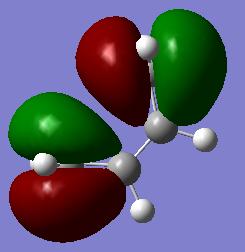
|
LUMO - yes HOMO - no |
| Quantum Mechanical 6-31G | 
|
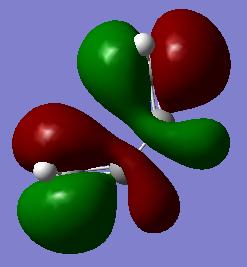
|
LUMO - yes HOMO - no |
References and Citations
- ↑ Balancing Dynamic and Nondynamic Correlation for Diradical and Aromatic Transition States: A Renormalized Coupled-Cluster Study of the Cope Rearrangement of 1,5-Hexadiene {(http://pubs.acs.org/doi/pdf/10.1021/ja044734d )}
- ↑ Common Conversion Factors in Computational Chemistry {(http://www.chem.arizona.edu/courseweb/074/CHEM5181/conversions.htm )}
- ↑ Infrared Spectrscopy {(http://www.cem.msu.edu/~reusch/VirtualText/Spectrpy/InfraRed/infrared.htm )}