Rep:Transition states (st4215): Exercise 3

Exercise 3: Diels-Alder vs Cheletropic

In this exercise, we examine the possible reactions between o-xylylene and SO₂ - the Diels-Alder reaction and the cheletropic reaction, as illustrated in the reaction scheme below.

Reaction of o-xylylene and SO₂ (Source)

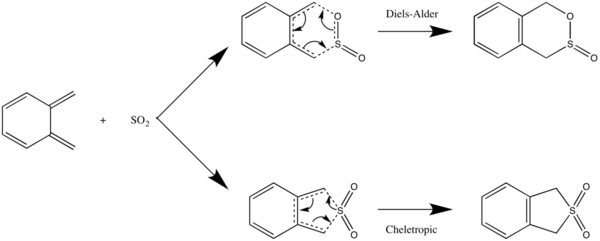
Again, in the Diels-Alder reaction, the dienophile SO₂ can approach the diene o-xylylene at different orientations, resulting in the endo- and exo- DA products. The cheletropic reaction, which is a pericyclic reaction in which the new bonds formed are made to the same atom, results in a single product.

In this exercise, we compare the three different reaction pathways - both Diels-Alder reactions and the cheletropic reaction - in terms of their reaction coordinates, as well as which is the most thermodynamically or kinetically favoured. We also investigate the possibility of a Diels-Alder reaction at a second site in xylylene.

Calculations

Calculations were performed at the PM6 level. Method 3 (see tutorial) was used to locate the transition state.

The optimised molecules can be seen here:

Reactants
o-xylylene	SO2

	Diels-Alder		Cheletropic
	Endo	Exo
Transition state	IRC file	IRC file	IRC file
Product

Reaction coordinate

Visualise the reaction coordinate with an IRC calculation for each path. Include a .gif file in the wiki of these IRCs.

The formation of the products for each of the endo- and exo- Diels-Alder reactions, as well as the cheletropic reaction, can be visualised below.

Diels-Alder		Cheletropic
Endo	Exo

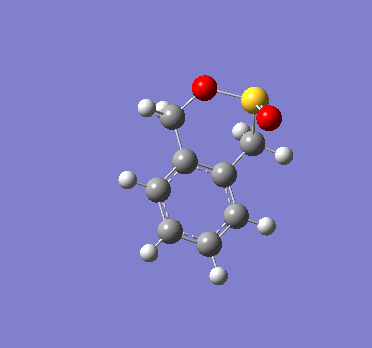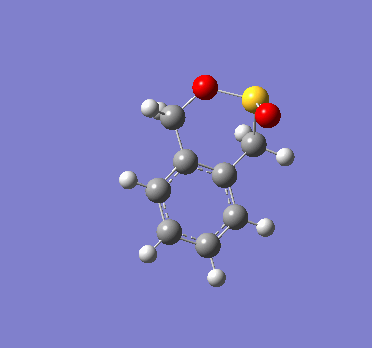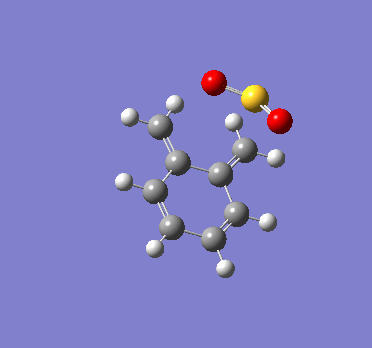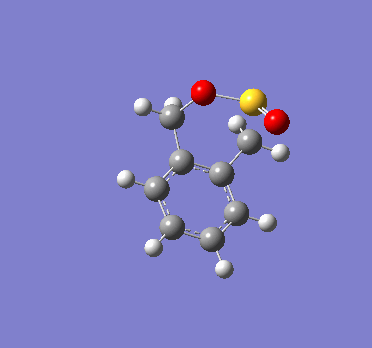
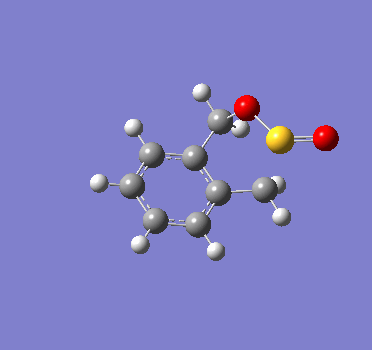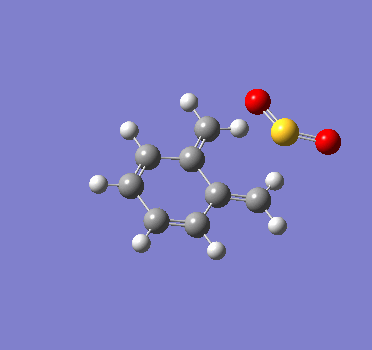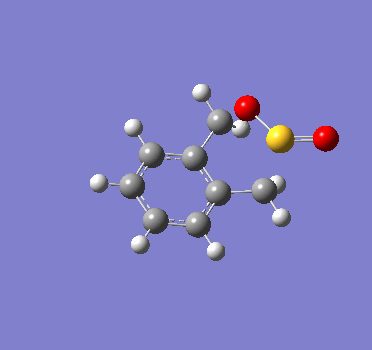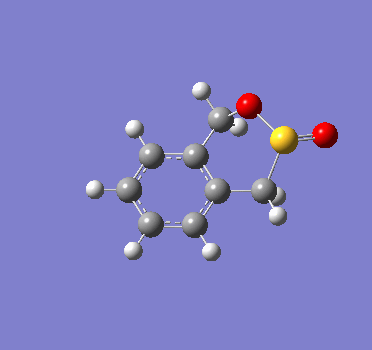
We can see that SO₂ approaches xylylene at a different orientation and angle for each of these reactions. This difference in approach trajectories hence lead to the formation of different products.

It can also be observed that in each of the reactions, as the product is formed, the 6-membered ring in xylylene becomes aromatic. This means that there is a strong driving force for the formation of the products. In contrast, the reactant xylylene is highly unstable as it is non-aromatic, and as can be seen in these reactions, can readily react with unsaturated bonds to form a more stable aromatic product.

Energy analysis

Calculate the activation and reaction energies (converting to kJ/mol) for each step as in Exercise 2 to determine which route is preferred. Using Excel or Chemdraw, draw a reaction profile that contains relative heights of the energy levels of the reactants, TSs and products from the endo- and exo- Diels-Alder reactions and the cheletropic reaction. You can set the 0 energy level to the reactants at infinite separation.

Free energies

The free energies of the reactants, transition states and products for each of the 3 reactions are tabulated below. The reaction barriers and energies are also calculated.

	Energy at 298 K (PM6)
	Hartree	kJmol-1
Reactants
Xylylene	0.17876	469.34
SO2	-0.11927	-313.14
Total reactants	0.059496	156.21
Endo- Diels-Alder
Transition state	0.090560	237.77
Product	0.021704	56.984
Reaction barrier (Ea)	0.0311	81.6
Reaction energy (ΔG)	-0.0378	-99.2
Exo- Diels-Alder
Transition state	0.092078	241.75
Product	0.021455	56.330
Reaction barrier (Ea)	0.0326	85.5
Reaction energy (ΔG)	-0.0380	-99.9
Cheletropic
Transition state	0.099058	260.08
Product	-0.000002	-0.0052510
Reaction barrier (Ea)	0.0396	104
Reaction energy (ΔG)	-0.0595	-156

^Note that all values from the calculations are reported to 5 s.f. unless more decimal places are needed to differentiate between each reaction type. Derived quantities (reaction barrier and reaction energy) are reported to 3 s.f.

Thermodynamic and kinetic products

From the values above, a combined reaction profile showing the reaction barriers and reaction energies can also be plotted as seen below.

Reaction profile diagram for the 3 Diels-Alder and cheletropic reactions, setting the energy of the reactants to zero

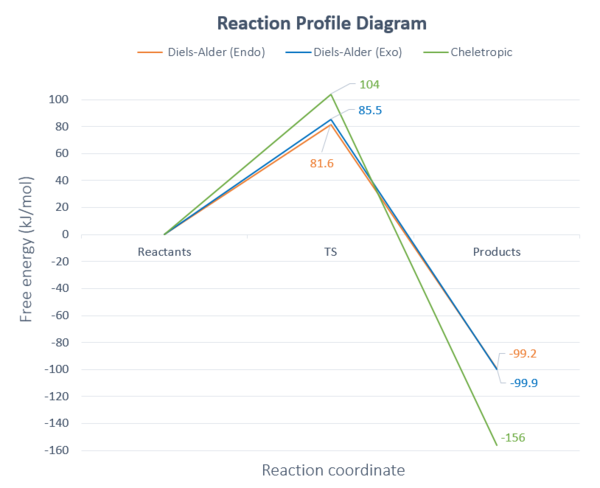
We can clearly see that the endo- Diels-Alder product is the kinetic product as it has the lowest reaction barrier of +81.6 kJmol^-1, while the cheletropic product is the thermodynamic product as it is most stable as has the lowest energy of -156 kJmol^-1. This is consistent with experimental and computational data.

The high stability of the cheletropic product is likely due to its high symmetry, which minimises steric clash, as well as the preference of S to adopt a five-membered compared to 6-membered ring structure. This is in contrast to saturated carbon rings, where 6-membered cyclohexane is more stable than 5-membered cyclopentane due to deviation from tetrahedral bond angles of 109° in cyclopentane, resulting in angle strain. However, due to the larger size of the S atom, C-C_tet-S bond angles in a 5-membered unsaturated sulfur ring (like in the cheletropic product) are much closer to the tetrahedral bond angle, at 105°. In comparison, the 6-membered heterocycle in the Diels-Alder products have C-C_tet-S bond angles of around 114°, which are comparatively larger than 109°. This is illustrated below:

	Diels-Alder		Cheletropic
	Endo	Exo
Products

(Nice analysis. I would think that it's mostly because the Diels-Alder products are highly distorted due to the size of the sulfur atoms. This creates ring strain, which is largely from the inefficient sp3 hybridisation that results from having to twist the structure. The cheletropic product doesn't suffer from this Tam10 (talk) 11:22, 30 October 2017 (UTC))

It is also expected that one of the Diels-Alder products (the endo- product) is the kinetic product instead of the cheletropic product. While the reaction barriers for both endo- and exo- Diels-Alder reactions are similar, the reaction barrier for the cheletropic reaction is much higher. Examining their transition states (see below) allows us to infer why.

	Diels-Alder		Cheletropic
	Endo	Exo
Transition state HOMO
Discussion	Some stabilising secondary orbital interactions can be seen in the HOMOs of the endo- and exo- transition states, hence lowering its energy and reducing the reaction barriers for these reactions.		No stabilising secondary orbital interactions are present here - in fact, the HOMO of the transition state is highly antisymmetric with many nodes, and hence likely to be high in energy.

Like most Diels-Alder reactions, the endo and not the exo- product is the kinetic product due to more or greater stabilising secondary orbital interactions in the transition state. However, in this reaction, both the endo- and exo- transition states seem to have an approximately equal but not significant amount of stabilising orbital interactions in the HOMO. This explains why the endo- and exo- transition states are relatively close in energy.

(Very good - not many people try to rationalise the kinetics with MOs. Here it's less obvious than exercise 2. Tam10 (talk) 11:22, 30 October 2017 (UTC))

Extra: Diels-Alder reaction at a different site

O-xylylene also contains a cis-butadiene fragment that can act as the diene in another Diels-Alder reaction. However, this reaction is very kinetically and thermodynamically favourable, as proven by computational methods.

Calculations

Calculations were performed at the PM6 level. Method 3 (see tutorial) was used to locate the transition state.

The optimised molecules can be seen here. Optimised reactants (o-xylylene and SO₂) from the earlier reaction were used.

	Diels-Alder (2)
	Endo	Exo
Transition state	IRC file	IRC file
Product

Energy analysis

The free energies of the reactants, transition states and products for both the endo- and exo- Diels Alder reactions are tabulated below. The reaction barriers and energies are also calculated.

	Energy at 298 K (PM6)
	Hartree	kJmol-1
Reactants
Xylylene	0.17876	469.34
SO2	-0.11927	-313.14
Total reactants	0.059496	156.21
Endo- Diels-Alder (2)
Transition state	0.10207	267.99
Product	0.065613	172.27
Reaction barrier (Ea)	0.0426	112
Reaction energy (ΔG)	+0.00612	+16.1
Exo- Diels-Alder (2)
Transition state	0.10505	275.82
Product	0.067305	176.71
Reaction barrier (Ea)	0.0456	120
Reaction energy (ΔG)	+0.00781	+20.5

^Note that all values from the calculations are reported to 5 s.f. unless more decimal places are needed to differentiate between each reaction type. Derived quantities (reaction barrier and reaction energy) are reported to 3 s.f.

We can hence see that this reaction is both kinetically and thermodynamically unfavourable compared to the other Diels-Alder reaction (previously discussed) and the cheletropic reaction.

Comparing the reaction barriers, the activation energies of 112 kJmol^-1 (endo) and 120 kJmol^-1 (exo) are much higher than that of the other DA reaction, at 81.6 kJmol^-1 (endo) and 85.5 kJmol^-1 (exo), as well as the cheletropic reaction, at 104 kJmol^-1. Hence this Diels-Alder reaction is the most kinetically unfavourable reaction.

Comparing the reaction energies, we can see that both the endo- and exo- reactions are endothermic - compared to the other two DA reactions as well as the cheletropic reaction, which are exothermic. This indicates that this Diels-Alder reaction is also highly thermodynamically unfavourable as ΔG<0 and it is not spontaneous.

(Very good! Tam10 (talk) 11:27, 30 October 2017 (UTC))

Conclusion

While there are several possible reactions between o-xylylene and SO₂, including a Diels-Alder reaction at two different sites and a cheletropic reaction, not all are comparable in terms of kinetic and thermodynamic favourability. Calculations show that the cheletropic reaction is the most thermodynamically favoured due to the higher stability of a 5-membered S ring, and the Diels-Alder reaction between the two terminal alkene carbons of xylylene is much more kinetically and thermodynamically favourable compared to the Diels-Alder reaction involving the cis-butadiene fragment in the aromatic 6-membered ring. This is because the aromaticity of the ring is not broken in the former reaction.