Rep:Transition states (st4215): Exercise 1
Exercise 1: Reaction of Butadiene with Ethylene
The reaction between butadiene and ethylene is a [4+2] cycloaddition reaction, or more specifically, a Diels-Alder reaction - a reaction involving a conjugated diene in the s-cis conformation, and a dienophile containing a double bond. In this simple Diels-Alder reaction, butadiene is the diene and ethylene is the dienophile. The reaction scheme for this reaction is shown below:
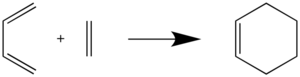
In this exercise, we use this Diels-Alder reaction to determine the orbital symmetry requirements for a reaction to take place, and to show the effect of hybridisation and bond order on the length of C-C bonds. We also probe into the mechanism of the reaction, and determine if bond formation is synchronous or asynchronous.
(Fv611 (talk) 17:17, 1 November 2017 (UTC) Very well done on the exercise as a whole!)
Calculations
Calculations were performed at the PM6 level. Method 1 (see tutorial) was used to locate the transition state.
The optimised molecules can be seen here:
| Reactants | Transition state | Product | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
| ||||||||||||
Molecular orbitals
MO diagram
Construct an MO diagram for the formation of the butadiene/ethene TS, including basic symmetry labels (symmetric/antisymmetric or s/a).
The MO diagram for this cycloaddition reaction was constructed as shown below. We first assume based on prior knowledge that only orbitals of the same symmetry can combine; however, this is proven in a later section.
The MOs have been labelled accordingly with their numbers according to the calculations, and can be visualised in the section below.
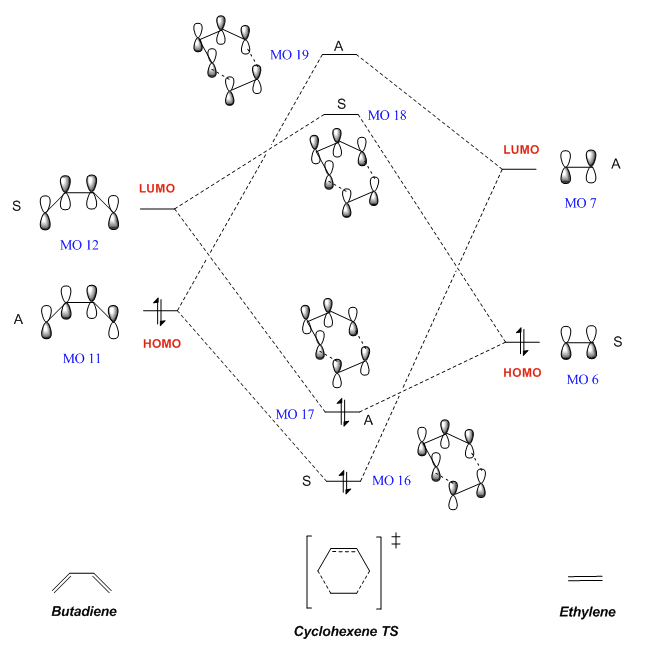
Considering the actual energy levels of the MOs computed from the calculations, a more accurate MO diagram can be constructed, as seen here. However, this does not affect the relative energy levels of the MOs (within each molecule) or the interactions between these MOs.
Computed MOs
Include images (or Jmol objects) for each of the HOMO and LUMO of butadiene and ethene, and the four MOs these produce for the TS. Correlate these MOs with the ones in your MO diagram to show which orbitals interact.
The HOMOs and LUMOs for each reactant, butadiene and ethylene, as well as the 4 MOs that these produce for the TS, were calculated and can be visualised below. The MO numbers correspond to that labelled on the MO diagram, allowing us to see which orbitals interact. We can also observe that these computed MOs bear physical resemblance to that drawn in the MO diagram, in terms of the bonding and antibonding phases in each MO.
| Symmetry | Reactants | Transition state | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Butadiene | Ethylene | |||||||||||
| Antisymmetric | MO 11 (HOMO) |
MO 7 (LUMO) |
MO 16 |
MO 19 | ||||||||
| Symmetric | MO 12 (LUMO) |
MO 6 (HOMO) |
MO 17 |
MO 18 | ||||||||
Symmetry requirements
What can you conclude about the requirements for symmetry for a reaction (when is a reaction 'allowed' and when is it 'forbidden')? Write whether the orbital overlap integral is zero or non-zero for the case of a symmetric-antisymmetric interaction, a symmetric-symmetric interaction and an antisymmetric-antisymmetric interaction.
From the table above as well as the MO diagram, we can see that the HOMO/LUMO of butadiene interact with the corresponding LUMO/HOMO in ethylene respectively. These interactions can occur as each pair of orbitals share the same symmetry. The HOMO of butadiene (MO 11) and the LUMO of ethylene (MO 7) are both antisymmetric, and interact to give two antisymmetric MOs in the TS (MOs 16 and 19). Similarly, the LUMO of ethylene (MO 12) and the HOMO of butadiene (MO 6) are both symmetric, and interact to give two symmetric MOs in the TS (MOs 17 and 18). (Fv611 (talk) 17:17, 1 November 2017 (UTC) You mean the LUMO of butadiene and the HOMO of ethylene ;) ) Hence we can conclude that a reaction is only allowed when the relevant orbitals share the same symmetry, as this would allow orbitals to overlap and thus interact. This is illustrated in the following table:
| Symmetry of interaction | Orbital overlap integral |
|---|---|
| Symmetric-antisymmetric | Zero |
| Symmetric-symmetric | Non-zero |
| Antisymmetric-antisymmetric | Non-zero |
C-C bond lengths
Include measurements of the 4 C-C bond lengths of the reactants and the 6 C-C bond lengths of the TS and products. How do the bond lengths change as the reaction progresses? What are typical sp3 and sp2 C-C bond lengths? What is the Van der Waals radius of the C atom? How does this compare with the length of the partly formed C-C bonds in the TS.
The C-C bond lengths in the reactants, TS and products are tabulated below.
| Reactants | Transition state | Product | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Butadiene | Ethylene | ||||||||||||
| Labelled C atoms | |||||||||||||
| C-C bond length / Å |
Bond A | ||||||||||||
| Bond B | |||||||||||||
| Bond C | |||||||||||||
| Bond D | |||||||||||||
| Bond E | |||||||||||||
| Bond F | |||||||||||||
From the values above, we can observe the following changes in bond length as the reaction progresses.
| Bond | Trend in bond length as reaction progresses | Graph |
|---|---|---|
| A | As the reaction progresses, the length of Bond A increases. This is because Bond A is initially a C=C double bond in butadiene, which becomes a sp2-sp3 C-C single bond in cyclohexene. These lengths are similar to typical values of 1.34 Å for alkenes and 1.50 Å sp2-sp3 C-C bonds.[1] | 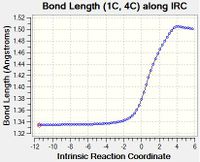
|
| B | As the reaction progresses, the length of Bond B decreases. This is because Bond B is initially an sp2-sp2 C-C single bond in butadiene, which becomes a C=C double bond in cyclohexene. These lengths are similar to typical values of 1.47 Å for sp2-sp2 C-C bonds and 1.34 Å for alkenes.[1] | 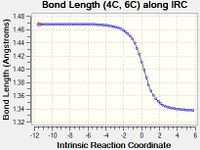
|
| C | Similar to Bond A, as the reaction progresses, the length of Bond C increases. This is due to the same reason as explained for Bond A. | 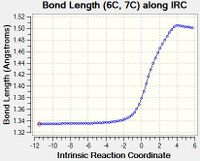
|
| D | As the reaction progresses, the length of Bond D increases. This is because Bond B is initially an C=C single bond in ethylene, which becomes a sp3-sp3 C-C single bond in cyclohexene. These lengths are similar to typical values of 1.34 Å for alkenes and 1.54 Å for sp3-sp3 C-C bonds.[1] | 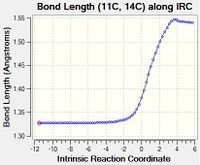
|
| E | Bond E is formed in this reaction. Hence as the reaction progresses from the transition state to the product, the length of Bond E increases. The length of the fully formed Bond E in the product, an sp3-sp3 C-C single bond, corresponds to the typical value of 1.54 Å.[1] The distance between the C atoms in the TS (2.11 Å) falls between twice the van der Waal radius of C (2 x 1.70 Å[2] = 3.40 Å) and the length of the fully formed Bond E, indicating that the atoms are approaching each other. | 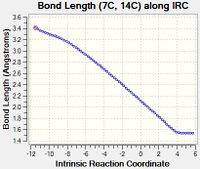
|
| F | Like Bond E, Bond F is also formed in this reaction. Hence as the reaction progresses from the transition state to the product, the length of Bond F increases, due to the same reasons as explained above. | 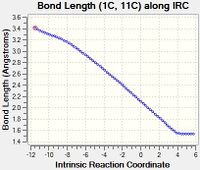
|
We can hence conclude that bond lengths in the reactants and product do not deviate from typical values. Additionally, we can also show that an increase in bond order from 1 to 2 indeed shortens the C-C bond, while an increase in hybridisation from sp2 to sp3 does lengthen the C-C bond, as seen in the comparison of theoretical values.
Transition state
Illustrate the vibration that corresponds to the reaction path at the transition state. Is the formation of the two bonds synchronous or asynchronous?
As illustrated above, the formation of the two bonds are synchronous as the relevant pairs of atoms (C1/C11 and C7/C14) are moving towards each other at the same time, with the distance between the two atoms being approximately equal in both pairs. This is to be expected as evidence shows that the Diels-Alder reaction can proceed via a concerted, synchronous mechanism.[3] However, it is important to note that this may also be the result of the calculation method used, as studies with other calculation methods (DFT/B3LYP) have also shown that other mechanisms are feasible.[4]
Conclusion
By examining this simple Diels-Alder reaction between butadiene and ethylene, we can conclude from computational data that only orbitals need to share the same symmetry to be able to overlap and hence interact. This knowledge will be useful in Exercise 2, where we again construct a MO diagram for a another Diels-Alder reaction. By following the change in C-C bond lengths over the course of the reaction, it can also be concluded that as per theoretical data, bond lengths shorten when bond order increases and hybridisation decreases. Lastly, based on this calculation, we can conclude that the Diels-Alder reaction between butadiene and ethylene proceeds via synchronous bond formation in the transition state.
References
- ↑ 1.0 1.1 1.2 1.3 M. A. Fox, J. K. Whitesell, E. Buchholz. Organische Chemie: Grundlagen, Mechanismen, bioorganische Anwendungen (1995).
- ↑ A. Bondi. van der Waals Volumes and Radii J. Phys. Chem. 68(3), 441–451 (1996).
- ↑ K. N. Houk, Y. T Lin & F. K. Brown. Evidence for the Concerted Mechanism of the Diels-Alder Reaction of Butadiene with Ethylene. J. Am. Chem. SOC. 108, 554-556 (1986).
- ↑ E. Goldstein, B. Beno & K. N. Houk. Density Functional Theory Prediction of the Relative Energies and Isotope Effects for the Concerted and Stepwise Mechanisms of the Diels-Alder Reaction of Butadiene and Ethylene J. Am. Chem. Soc. 118, 6036-6043 (1996).
