Rep:Transition states (st4215)
Introduction
In a chemical reaction, reactants can change into the products via a multitude of different configurations of atoms, each with a different energy. These energies corresponds to a energy profile (when there is 1 degree of freedom), or a Potential Energy Surface (PES) (when there are two degrees of freedom). An example of the PES for a reaction can be seen below.
Nf710 (talk) 23:47, 7 November 2017 (UTC) A PES can be N dimensions it can just be visualised in 2.
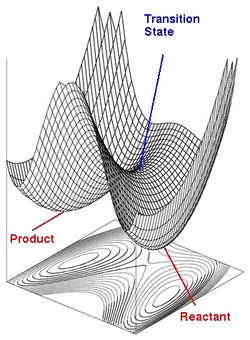
As illustrated in the PES, the reactants and products correspond to energy minima - where energy increases in all directions, meaning that the reactants and products sit in a well. At this point, the gradient of the PES curve is zero, and the second derivative yields a positive value, indicating it is a minimum.
The reaction coordinate is hence the minimum energy pathway that leads from the reactants to the products, where the maximum energy along this pathway corresponds to the transition state. In terms of the PES, this corresponds to a first-order saddle point - where energy increases in all directions but one. At this point, the gradient of the PES curve is also zero - it is both a maximum and a minimum. However, the second derivative leads a negative value, indicating that energy is a maximum in one direction but a minimum in all other directions. This value is a negative force constant which corresponds to the imaginary frequency in the vibration spectrum of the transition state. The normal mode corresponding to this imaginary frequency usually show the relevant atoms of the reactants moving towards each other to form the product.
Nf710 (talk) 23:51, 7 November 2017 (UTC) A few points, You haven't defined what you meant by direction. The second derivative is negative in the reaction coored and all other are positive.
Hence the presence of a negative imaginary frequency in the transition state calculation confirms that the structure at a saddle point and hence corresponds to the transition state. However, energy minima where reactants and products lie should not contain any imaginary frequencies, as the second derivative only yields positive force constant values. The lack of imaginary frequencies in a frequency calculation can confirm that the structures lie in energy minima, and correspond to either the reactants or products.
In this module, computational methods were used to locate and characterise transition states for various pericyclic reactions, including Diels-Alder and cheletropic reactions. An overview of the various methods that were used in the calculations are detailed here.
Nf710 (talk) 23:51, 7 November 2017 (UTC) A good explanation of a TS however, you could have spoke in abit moe detail about the Quantum mechanical methods used.
Exercises
The instructions for the exercises can be found here.
Exercise 1: Reaction of Butadiene with Ethylene
The reaction between butadiene and ethylene is a [4+2] cycloaddition reaction, or more specifically, a Diels-Alder reaction - a reaction involving a conjugated diene in the s-cis conformation, and a dienophile containing a double bond. In this simple Diels-Alder reaction, butadiene is the diene and ethylene is the dienophile. The reaction scheme for this reaction is shown below:
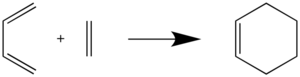
In this exercise, we use this Diels-Alder reaction to determine the orbital symmetry requirements for a reaction to take place, and to show the effect of hybridisation and bond order on the length of C-C bonds. We also probe into the mechanism of the reaction, and determine if bond formation is synchronous or asynchronous.
The link to this completed exercise can be found here.
Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole
The reaction of cyclohexadiene and 1,3-dioxole is also a Diels-Alder reaction, in which cyclohexadiene is the diene and 1,3-dioxole is the dienophile. However, unlike the simple Diels-Alder reaction between butadiene and ethylene, this reaction is slightly more complex - 1,3-dioxole can approach the diene at different orientations, leading to the formation of the endo- and exo- Diels-Alder products. This can be seen in the reaction scheme below:
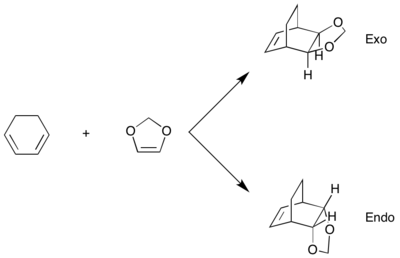
The endo- product is formed from a transition state where the substituents on the dienophile point towards the π system of the diene, while the exo- product is formed from a transition state where the substituents are pointing away.
In this exercise, we take a closer look at a different aspect of the Diels-Alder reaction - whether it is normal or inverse electron demand. We also consider the Diels-Alder reaction when an unsymmetrical diene is involved, and compare the endo- and exo- DA reactions in terms of which is more kinetically or thermodynamically favourable. In the process, we confirm that the orbital symmetry requirements as elucidated in Exercise 1 still apply, and illustrate that there are differences between the PM6 and B3LYP calculation methods, with one being more suitable than the other in this case.
The link to this completed exercise can be found here.
Exercise 3: Diels-Alder vs Cheletropic
In this exercise, we examine the possible reactions between o-xylylene and SO2 - the Diels-Alder reaction and the cheletropic reaction, as illustrated in the reaction scheme below.
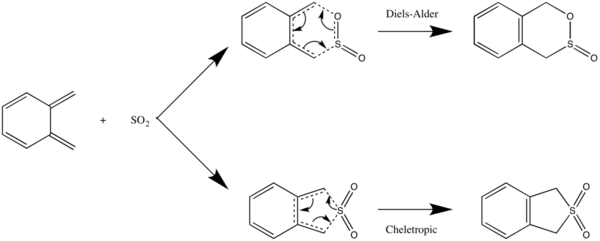
Again, in the Diels-Alder reaction, the dienophile SO2 can approach the diene o-xylylene at different orientations, resulting in the endo- and exo- DA products. The cheletropic reaction, which is a pericyclic reaction in which the new bonds formed are made to the same atom, results in a single product.
In this exercise, we compare the three different reaction pathways - both Diels-Alder reactions and the cheletropic reaction - in terms of their reaction coordinates, as well as which is the most thermodynamically or kinetically favoured. We also investigate the possibility of a Diels-Alder reaction at a second site in xylylene.
The link to this completed exercise can be found here.
Conclusion
Note: Please see each exercise for conclusions pertaining to that exercise
Computational methods allowed us to successfully examine the various pericyclic reactions, by locating and characterising their transition states via a variety of methods. In the process, we were able to determine the kinetic and thermodynamic products of each reaction, prove that orbitals must share the same symmetry in order to interact, and construct MO diagrams based on calculations, among others.
